Paradoxe de Langevin.................................................................................................................. 2
1- Rappel du paradoxe :Rappel de Relativité Restreinte.............................................................. 2
2- 1 Exemple concret : Les jumeaux sont Terence (le sédentaire) et Stella ( la
voyageuse)............ 3
2-2 L'Explication
par le Diagramme d'espace Temps.................................................................. 4
2-3 L'Explication
par l'Effet Doppler : Ce que Terence et Stella voient
réellement de leurs propres yeux......................................................................................................................................... 6
2-4 Le Paradoxe de Langevin
: L'Explication de la "Relativité Générale"...................................... 8
2-5 Les Objections : 2-5-1
L'objection de discontinuité temporelle............................................. 10
2-5-2 : L'
Objection de dépendance de la distance.................................................................... 12
2-5-3 Trop d'explications:
une Méta-Objection......................................................................... 13
3- Vérifications
expérimentales................................................................................................. 15
4- Conclusion......................................................................................................................... 15
5- Références:......................................................................................................................... 16
1- Albert Einstein : Relativités 1
: Seuil-CNRS F. Balibar........................................................... 16
2- Henri Poincaré: Une
contribution décisive à la Relativité : C. Marchal ( document
communiqué par Mr G. Hoynant)................................................................................................................ 16
3- Le temps et sa flèche ( Matière Espace Temps par JP Luminet)
: Champs Flammarion........... 16
4 - The Twin Paradox http://math.ucr.edu/home/baez/physics/Relativity/SR/TwinParadox/twin_paradox.html.............. 16
5 - Le paradoxe de Langevin ( traduction du document ci dessus)............................................. 16
6- Introduction à la relativité
générale Luc Blanchet.................................................................. 16
7- Géométries: Relativité
Restreinte et initiation à la physique mathématique : S. Poirier ; http://spoirier.lautre.net............................................................................................................ 16
Annexe................................................................................................................................... 16
Paradoxe de Langevin
1- Rappel du paradoxe :Rappel de Relativité Restreinte ( RR)
Selon la Relativité Restreinte, un observateur
du référentiel X, voit le temps s'écouler plus lentement dans un référentiel X'
animé d'une vitesse uniforme par rapport à son propre référentiel galiléen* ( il voit les horloges du système en mouvement
battre plus lentement que les siennes !), et en vertu du principe de
Relativité X' voit les horloges de X également battre plus lentement! Ce
ralentissement devient d'autant plus sensible que la vitesse s'approche de
celle de la lumière .
* qui ne subit pas d'accélération de quelque nature que ce soit =
système inertiel, la vitesse relative correspond à une situation établie ( on ne dit pas
comment X', a acquis une vitesse par rapport à X ou l'inverse).
Les temps sont
dans le rapport ( 1-v²/c²)-1/2,
les longueurs subissent exactement le même sort !!!!.
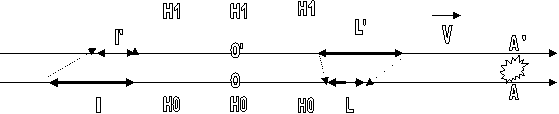
![]()
![]()
Ceci est la conséquence du principe de Relativité
Restreinte qui impose que les
lois soient les mêmes dans tous les référentiels inertiels (
pas de mouvement inertiel absolu). La
constance de la vitesse de la lumière n'est que le
choix du signal qui représente la vitesse maximum identique entre référentiels ( cf H. Poincaré). Ceci a des implications profondes sur la causalité et la relation entre le temps
et l'espace qui bien que gardant leur nature propre ne sont plus indépendants).
En langage moderne, on parle d'invariance des lois vis à vis d'un groupe
de transformations, de symétries
globales.
C'est le groupe
de H. Poincaré formé de 4 translations, 3 rotations réelles et 3 rotations
"imaginaires": propulsions.
L'espace temps ( sym.max)
de Minkowski associé possède ces symétries, les conférant aux phénomènes qui s'y déroulent.
A noter: Le principe
de Relativité Générale étend cette invariance globale en invariance locale de
jauge (symétrie de jauge)
Quelques FAQ pour
tordre le cou à quelques idées reçues sur la RR !!!
FAQ 1 : Les
contractions d'espace et de temps de la RR sont elles réelles ?
Réponse
habituelle : Non !
Réponse plus
correcte : Cette question n'a pas de sens en RR : Réelles par rapport à
quoi, puisqu'il n'y a pas d'espace absolu ?
FAQ2: Peut on définir
la simultanéité entre deux évènements de deux référentiels différents? ( dans un même
référentiel pas de problème, on a une coordonnée unique de temps)
Réponse : Oui, si un point-événement A0 du référentiel R0 envoie un signal
lumineux vers un point-événement A1 du référentiel
R1, que A1 le renvoie immédiatement vers le référentiel R0 et qu'il est reçu en
B0 de R0, alors A1 est simultané au point événement M0 situé au " milieu
temporel" de A0-B0. Mais il est
facile de vérifier que cette simultanéité est "relative" et qu'un
troisième événement A2 d'un autre référentiel R2 qui serait simultané à A1 ne
le serait pas en général à M0.
FAQ3: N'est ce pas
gênant de ne pas pouvoir définir de contraction absolue du temps et de l'espace
?.
Réponse: Non, cela
signifie simplement que la RR suppose que ces critères ne correspondent à aucun
caractère physique ( mesurable)
2- En 1911, le physicien français Paul Langevin a imaginé
un exemple frappant de l'élasticité du temps, qui a connu une fortune
médiatique considérable sous le nom de "paradoxe des jumeaux".
2- 1 Exemple concret
: Les jumeaux sont Terence (le sédentaire) et Stella ( la
voyageuse): cf ref
4
![]()
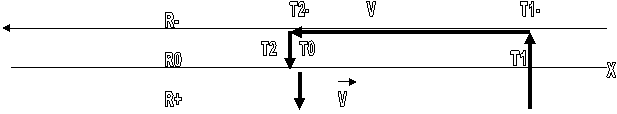
![]()
![]()
![]()
![]()
![]()
![]()
Malgré la
symétrie des équations, et l'apparente symétrie de la situation, la Relativité
Restreinte va nous montrer dans ce qui suit,
que c'est le voyageur qui vieillit le moins, d'où le paradoxe.
Nous ne traitons pas ici de
l'accélération de Stella au début et à
la fin du voyage: cela complique est n'est pas nécessaire à la compréhension du
paradoxe..
Nous
supposons que Stella passe en flèche dans son vaisseau spatial
, à côté de Terence
: Voici
l'itinéraire selon Terence.-
Début : Stella passe en
trombe à côté de moi. Nos chronomètres sont synchronisées
à 0.
Trajet aller
Stella
croise à presque 99 % de la vitesse de
la lumière (le facteur de dilatation de temps est de 7).
Disons que cette partie du voyage dure 7 ans (selon Terence, naturellement).
Demi tour: Stella met le feu à ses
moteurs pendant 1 jour pour inverser le
mouvement.
Trajet retour: Stella
croise vers la terre pendant 7 années à
la même vitesse qu'à l'aller..
Fin ( Retour) : Stella passe en trombe devant moi. Selon moi (Terence),
14 ans et un jour se sont écoulés entre le début et le retour.
Le chronomètre de Stella n'indique qu'à
peine plus que 2 ans*
Attention* : Ceci
ne veut pas dire que Stella a vécu ou vivra
plus longtemps que Terence , c'est juste une désynchronisation des temps propres, liée
à des conditions différentes.
2-2 L'Explication par le Diagramme d'espace Temps
Minkowski dit,
"dorénavant espace seul, et temps seul, sont condamnés se réduire à de
simples ombres, et seulement un genre d'union des deux en préservera une
Réalité indépendante." Minkowski a
projeté la version de la Relativité
Restreinte d'Einstein dans un nouveau cadre, l'espace temps de Minkowski. Le
paradoxe de Langevin a une résolution très simple dans ce cadre. Le concept crucial est le temps propre
d'un corps mobile.
Choisissons d'abord un référentiel
inertiel de référence, disons le référentiel repos de la terre (que nous
supposerons inertiel, même si ce n'est pas vrai). Une fois que nous avons choisi un référentiel
de référence, nous pouvons définir les coordonnées ( t, x, y, z) pour chaque événement qui a lieu. Si nous traçons tous
les événements de Terence et de Stella sur un diagramme Espace-temps de Minkowski.,
nous obtenons ce que nous appellerons leurs lignes d'univers.
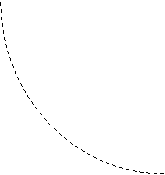
Les lignes d'univers de Terence et de Stella sont montrées sur la figure 1
Puisque Terence
est au repos dans notre référentiel choisi comme référence, à tout moment il
sera au le même endroit, tout le temps, disons (0.0.0). En d'autres termes, les
coordonnées de ses événements prennent
toutes la forme: (t,0,0,0).
Mais à un temps arbitraire,
les coordonnées évènementielles de Stella
vont prendre la forme: [ t, f(t), g(t), h(t)]
Où, f (t), g (t), et h (t) sont toutes des fonctions de t. La métrique de Minkowski est
décrite par la formule suivante:
ds² =
dt² = dt² -dx²-dy²-dz² donc t = òdt = ò [1-v²(t) ]1/2 . dt , avec v(t) = ( dx/dt, dy/dt,
dz/dt) ( on a posé c=1)
qui est le vecteur de
vitesse, et [ v
(t) ]² est le carré de sa longueur:
[ v(t)]²
= (dx/dt)² + (dy/dt)² + ( dz/dt)².
Les coordonnées de Terence sont toujours ( t , 0, 0, 0), ainsi dx , dy et dz sont toujours nuls pour lui.
Ainsi dt = dt , et l'intégrale devient: òdt = òdt = t.
Maintenant qu'en est il de Stella?
Pour elle, les dx , dy , et dz ne sont pas toujours nuls. Donc dx/dt , dy/dt
, et dz/dt ne
sont également pas toujours nuls, et leurs carrés (qui apparaissent dans la formule pour [ v (t)
]²) sont toujours non négatifs, et parfois positifs. Ainsi la quantité
sous la racine carrée est inférieure ou égale à 1, et parfois strictement
inférieure à 1. Conclusion:
la valeur de l'intégrale de Stella est inférieure à celle de l'intégrale de Terence. C.-à-d., son temps propre écoulé est inférieur à celui de Terence. C.-à-d., elle vieillit moins.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]()




![]()
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
Sur ce diagramme pour être lisible nous avons réduit le facteur de
dilatation temporel à environ 2.
S' = t' = Ö(t² -x²) représente le temps propre de Stella entre les évènements D et
R.
Comme dans cet exemple, comme la vitesse du
référentiel de Stella est constante le
rapport des "t"
entre Terence et Stella est constant , on
peut rendre compte de la métrique de Minkowski, sur une représentation "
Euclidienne" simplement en mesurant les longueurs des lignes d'univers de Terence et Stella
(leurs temps propres) par des unités différentes ( dont le rapport est égal à Ö( 1 -v²/c²): coordonnées curvilignes )
Voilà toute l'histoire! Nous évaluons une intégrale de temps
propre sur deux lignes d'Univers différentes, nous obtenons deux résultats
différents.
2-3 L'Explication par l'Effet Doppler : Ce que Terence
et Stella voient réellement de leurs propres yeux
Equipons les des télescopes
incroyablement puissants, ainsi chaque jumeau peut observer l'autre horloge qui
émettra des éclairs toutes les secondes pendant tout le voyage.
Sur la Trajet aller, Terence voit
approximativement un éclair toutes les 14 secondes sur l'horloge de Stella.
Sur la Trajet retour, il voit l'horloge de Stella clignoter
à environ 14 éclairs par seconde.
Stella voit le même comportement vis à vis de l'horloge de Terence.
Les facteurs d'effet Doppler
que j'ai donnés (1/14 et 14/1) sont issus de la formule relativiste de l'effet
Doppler. La formule relativiste tient
compte et du retard lié à la distance de la formule non-relativiste,
et de la dilatation relativiste de temps.
En d'autres termes, Terence calcule que l'horloge de Stella bat 7
fois moins vite tout le temps, mais il la voit fonctionner
plus rapidement pendant la Trajet retour parce que chaque éclair a une distance
plus courte à parcourir. Et Stella
calcule la même chose pour Terence.
Très bien
, mais tout ceci ne semble que contribuer à durcir le paradoxe! Stella voit ce que Terence
voit : une
horloge qui musarde sur le trajet aller et une horloge qui essaie de rattraper
le temps perdu sur le trajet retour.
D'où vient l'asymétrie entre Stella et Terence?
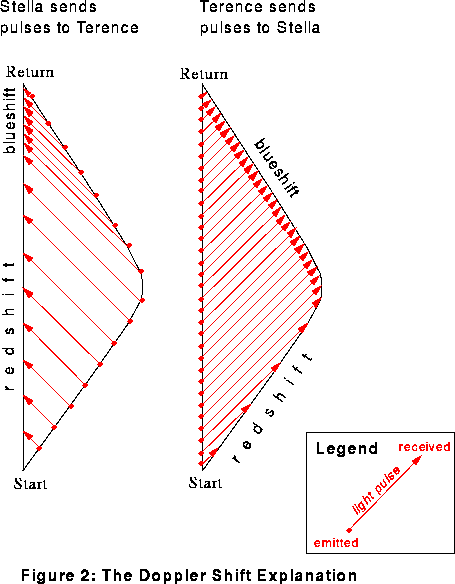
Réponse: Examinons
le diagramme de la figure 2:
Sur le diagramme de gauche, Terence
"voit" Stella faire demi tour, au bout 13 ans 10 mois de son temps
propre,il va la "voir" vieillir ensuite rapidement pendant les 2 mois suivants de son
temps propre, mais cela survient trop tard.
Sur le diagramme de droite lorsque Stella fait son demi
tour, au bout d'un an de son temps propre, elle "voit" Terence vieilli de 2 mois, elle va le "voir"
vieillir rapidement de 13 ans 10 mois pendant son retour qui dure un an de son
temps propre.
![]()
2-4 Le Paradoxe de Langevin : L'Explication de la "Relativité Générale"
L'appellation est un peu cavalière. Ce
qui explique les guillemets dans ce chapitre..
Quelques rappels de base : Cette explication se fonde
sur quelques affirmations de la RG.
· Libre
choix des référentiels de référence: Vous pouvez décrire la physique d'une situation depuis n'importe
quel référentiel à votre guise, mais quelques référentiels exigent
l'introduction de champs qui n'apparaissent pas dans d'autres
référentiels. Nous les appellerons
"champs de pseudo-force", ou même
"champs de gravitation".
· Dilatation uniforme "gravitationnelle" de temps: Si
vous avez deux horloges identiques . On place l'une au fond d'un puits de
potentiel "de gravitation" uniforme (ou puits "pseudo-potentiel" , si vous préférez) et on place l'autre plus haut,
l'horloge inférieure bat plus lentement
que l'horloge supérieure.
Le paradoxe de Langevin : Nous sélectionnons le référentiel
de Stella , et nous le déclarons au repos, tout le
temps!
Quand elle met à feu ses moteurs pour le demi tour, elle "constate"
qu'un champ "de gravitation" uniforme innonde
soudainement l'univers; le champ compense exactement la force de ses moteurs,
ainsi elle reste immobile.
Pas pour Terence. Le champ cause son accélération, ( du point de vue de Stella qui le voyait s'éloigner
régulièrement et qui voit maintenant sa vitesse d'éloignement ralentir puis
s'inverser et qui voit Terence se rapprocher en
tombant vers elle en chute libre, comme un projectile tiré verticalement dans
un champ de pesanteur), mais Terence ne sent
rien puisqu'il est en chute libre (ou
plutôt la terre dans son ensemble l'est).
Il y a une énorme différence de potentiel entre lui et Stella:
rappelez-vous, il est des années-lumière de Stella, dans un champ de
gravitation uniforme! Stella au fond du
puit de potentiel, il est au sommet (ou le serait si le puit n'était pas sans
fond ni sommet.). Ainsi par la dilatation uniforme "gravitationnelle" du temps, il vieillit de plusieurs années pendant le demi tour de Stella ( cf fig
3).
![]()
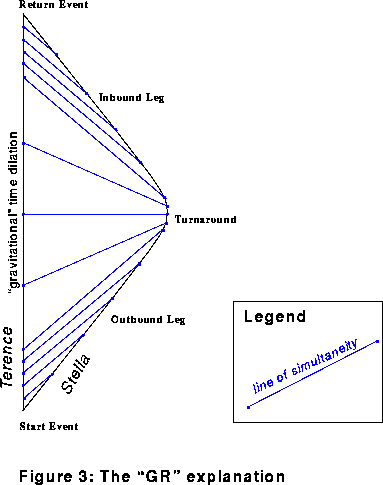
Figure
3: Le
diagramme relatif à l'explication par la relativité générale, est complété par
des lignes de simultanéité ( en bleu) au lieu
d'impulsions lumineuses. Ces lignes représentent le lieu géométrique des
événements qui se déroulent simultanément selon Stella .On peut voir comment
les lignes sont bien groupées sur la ligne d'Univers de Stella et dispersées
sur la ligne d'Univers de Terence. Ceci est une
représentation graphique de la dilatation gravitationnelle du temps.
2-5 Les Objections : 2-5-1 L'objection de
discontinuité temporelle
Supposons le demi tour instantané; la Relativité
impose une limite supérieure aux vitesses, mais pas aux accélérations.
Un demi tour instantané est un cas limite d'un demi
tour court, donc la théorie devrait traiter ce cas.
Pendant le trajet aller, Terence
vieillit de moins de 2 mois selon Stella (12 mois de Stella, Facteur de
dilatation temporel = 7).
Sur le trajet retour, Terence
vieillit pareil, car les mêmes calculs de Stella s'appliquent aussi. Si le demi
tour est instantané, il semblerait donc que Terence
n'ait vieilli que de 4 mois à peine. Pourtant on prétend que Terence a vieilli de 14 ans quand Stella le recroise au
retour ! Où sont donc passés les années manquantes ?
L'explication par l'effet Doppler répond à cet
argument. Stella voit ( via son télescope) Terence vieillir très lentement sur le trajet aller , mais
prendre pratiquement 14 ans sur son trajet retour. Pas de discontinuité
temporelle !
Certes elle calcule quelque chose de différent en
tenant compte de l'effet Doppler et de la vitesse finie de la lumière. Ces
calculs sont valables pour des référentiels inertiels. En fait pour Stella,
elle obtient 2 mois pour le référentiel correspondant au le trajet aller et 2
mois sur le référentiel correspondant au trajet retour ( cf ci-dessus) , et pour obtenir 4 mois elle doit
additionner des quantités mesurées dans deux référentiels différents (elle a
changé "instantanément" de référentiel inertiel à mi course).
Mais des référentiels inertiels différents ont des critères
différents de simultanéité. Le référentiel "trajet aller" dit : "Au moment où
Stella fait son demi tour, l'horloge de Terence marque
environ 2 mois depuis le départ". Le référentiel du trajet
retour dit : " Au moment où Stella fait son demi tour, l'horloge de Terence marque environ 13 ans et 10 mois.
La prétendue
discontinuité n'est autre qu'une erreur de décompte des temps, causée par le
passage d'un référentiel à un autre.
L'explication par le diagramme d'espace
temps renvoie à la même solution. Quant à l'explication par la "RG"
l'objection de la "discontinuité temporelle", nous invite à
considérer la limite d'un demi tour instantané.
Mais dans cette limite le champ gravitationnel devient infini entraînant une
dilatation temporelle infinie. Ainsi Terence
vieillirait de
plusieurs années instantanément , ce qui est physiquement
irréaliste, comme un demi tour instantané.
En modifiant légèrement la
figure 3 nous obtenons une description correspondante à l'objection de
discontinuité temporelle
.
![]()
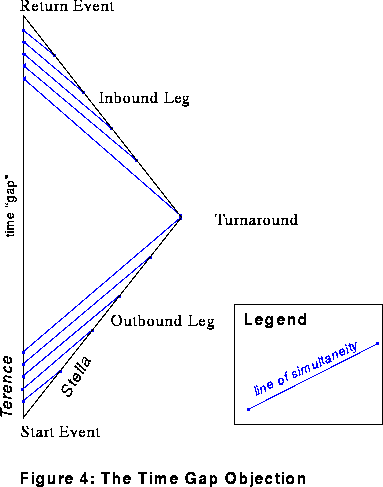
Ici nous avons supposé le demi tour
instantané. Sur le trajet Aller Stella
utilise un référentiel inertiel de référence et la même notion de simultanéité que
précédemment alors que sur le trajet retour elle commute vers un autre
référentiel
La discontinuité temporelle ( la partie de la ligne d'Univers de Terence
dépourvue de lignes bleues) est une conséquence de cette commutation brutale.
2-5-2 : L' Objection de dépendance de la distance.
Dans notre exemple standard ( voir
introduction) le calcul du vieillissement de Terence
par Stella est le suivant: 1/7 année pendant son trajet aller, 1/7 d'année
pendant le trajet retour et le reste 14 ans moins 2/7 d'année pendant le demi
tour.
Rappelons qu'elle fait son demi tour en un jour
selon Terence, soit environ 15 heures de son temps
propre à elle ( nous vous faisons cadeau des minutes
..).
Si Stella fait, dans les mêmes conditions, un voyage plus
long, prenant 2 ans au lieu d'un sur chacun des trajets aller et
retour soit un total de 4 ans de son temps propre, il s'écoulera 28 ans selon Terence. Mais si elle effectue le même demi tour, il
prendra le même temps ( 15 heures de son temps
propre).
Alors quand Stella et Terence
fêteront leurs retrouvailles fugaces, Terence aura
vieilli de 28 ans ( plus un jour). Stella décompte le
vieillissement de Terence comme suit: 2/7 d'années
sur le trajet aller, 2/7 d'année sur le trajet retour, donc Terence s'est pris, cette
fois ci, un coup de vieux de plus de 27 ans
pendant le demi tour, soit environ deux fois plus que dans notre exemple
standard, alors que Stella a opéré le demi tour dans le même temps, ce que Terence confirme.
La Solution est similaire à celle que nous avons
donnée pour l'objection de discontinuité temporelle. La façon dont Terence vieillit, n'est pas quelque chose que l'on peut
observer directement en RR. L'explication par l'effet Doppler s'appuie sur ce
que Terence et Stella voient vraiment avec leurs télescopes,
ce qui élude la difficulté. Le décompte de Stella est un décompte qui dépend du
référentiel inertiel, et pendant tout le demi tour elle change de façon
continue de référentiel inertiel.
Pas étonnant qu'un décompte qui ignore ce point
conduise à des résultats inattendus.
Dans l'explication de la RG, pas de mystère, la dilation
temporelle dépend de la différence de potentiel "gravitationnel", qui
dépend de la distance ( dans un champ uniforme).
2-5-3 Trop
d'explications: une Méta-Objection
Vieille
plaisanterie de prétoire:
"Votre Honneur, je vais d'abord montrer que mon
client n'a jamais emprunté le vase Ming du plaignant, ensuite qu'il a rendu le
vase en parfait état et enfin que la fêlure était déjà présente quand il l'a
emprunté."
Pourquoi tant d'explications ? Les tenants de la
Relativité chercheraient ils à noyer le poisson?
Pour valoir quelque chose le plaidoyer d'un avocat
de la défense n'a besoin que de semer le doute vis à vis du bien fondé de la
plainte.
Mais une
théorie physique doit nous tenir un discours homogène et cohérent.
La théorie paie ici le prix de sa versatilité. Elle
nous dit : Prenez le référentiel qui vous plait pour décrire vos résultats, ou
utilisez un diagramme d'espace temps et ne choisissez aucun référentiel privilégié.
Aucune importance: Cela n'est pas surprenant qu'une explication se décline en
plusieurs versions.
La
plupart des physiciens considèrent l'explication par le diagramme d'espace
temps comme l'explication fondamentale.
Sa nature géométrique fournit une trame Universelle
qui sert de support aux autres explications apparamment
différentes et montre quelles ne sont que différents aspects de la même.
Moralité : Un seul territoire, plusieurs cartes.
http://math.ucr.edu/home/baez/physics/Relativity/SR/TwinParadox/twin_paradox.html
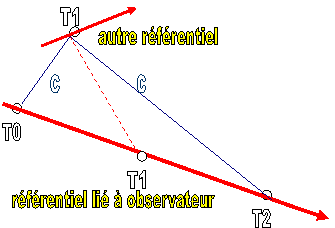
Ci
après une synthèse en représentation affine, qui montre le critère de
simultanéité, et les trois référentiels
impliqués ( celui de Terence,
ceux de Stella avant le demi tour et après) ainsi que leurs axes associées et
les trajectoires de la lumière (bleu)
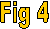

3- Vérifications expérimentales


L'expérience de
Langevin a été vérifiée avec des particules élémentaires appelées muons. Au CERN, on est capable d'accélérer un muon
jusqu'à ce qu'il atteigne la vitesse de 0,9994 c. Or, le muon est une particule
instable qui se désintègre au bout de 1,5 microseconde ; c'est son temps de vie
propre. Or, lorsqu'on mesure son temps
de vie apparent (dans le référentiel du laboratoire) on trouve 44
microsecondes, soit 30 fois plus - en parfait accord avec la Relativité
restreinte;
Horloge voyageuse qui à pris du retard :
Cela ressemble plus au cas indiqué ( le cas est
complexe car il faut tenir compte de nombreux effets, gravitation, accélération, cinématique )
4- Conclusion
On a vu que le paradoxe, lié au fait que
l'apparente symétrie des équations et du phénomène décrit n'entraîne pas
des vieillissements équivalents, est
brisé par le demi tour du voyageur. Alors la signification de ce
"paradoxe" est que dans des conditions différentes ou dans des
régions différentes de l'espace temps, le
temps propre des observateurs peut se dérouler différemment (
se désynchroniser).
Le temps propre de chaque observateur est
"immuable" puisqu'il est mesuré par une horloge qui lui est associée
(qui contrôle aussi son rythme biologique). C'est ce qui fait qu'on a pas la perception immédiate de l'interdépendance temps-espace.
Dans les conditions que nous connaissons,
tous les observateurs sont soumis aux ( presque) mêmes
conditions et que l'écart est infinitésimal, ce qui nous laisse à penser que
temps propre est le même pour tous.
Pour pouvoir constater cette différence
il faut partir d'une situation, où les temps propres sont
"synchronisés" et disymétriser la situation
et la re-symétriser plus tard pour que le constat soit
évident. Ceci nécessite des accélérations dans cette version du paradoxe.
Pour autant, celui qui voyage ne vit pas
plus vieux ( il n'a pas vécu 14 ans et vieilli de 2
ans, il a vécu 2 ans, et vieilli de 2 ans pendant que l'autre vivait 14 ans et
vieillissait de 14 ans ). Il ne s'agit donc pas d'une fontaine de Jouvence, on
peut par contre le considérer comme un saut dans le futur d'une civilisation ( sans retour).
.
5- Références:
1- Albert
Einstein : Relativités 1 : Seuil-CNRS
F. Balibar
2- Henri
Poincaré: Une contribution décisive à la Relativité : C. Marchal ( document communiqué par Mr G. Hoynant)
3- Le
temps et sa flèche ( Matière
Espace Temps par JP Luminet) : Champs Flammarion
4 - The Twin Paradox http://math.ucr.edu/home/baez/physics/Relativity/SR/TwinParadox/twin_paradox.html
5 - Le
paradoxe de Langevin ( traduction
du document ci dessus)
6-
Introduction à la relativité générale
Luc Blanchet
7-
Géométries: Relativité Restreinte et initiation à la physique mathématique : S.
Poirier ; http://spoirier.lautre.net
Annexes : P-Langevin-1.htm