Titre original: The twin paradox in compact spaces

Par John D. Barrow (1) et Janna Levin (1)(2)

(1) DAMTP, Cambridge University, Wilberforce Road, Cambridge CB3 0WA

(2) The Blackett Laboratory, Imperial College of Science, Technology & Medicine, South Kensington, London SW7 2BZ

http://arxiv.org/pdf/gr-qc/0101014

Traduction par J. Fric, qui endosse toute responsabilité pour les erreurs que sa traduction auraient pu introduire. Commentaires entre [..]

Le Paradoxe des Jumeaux dans un espace compact

Résumé

Des jumeaux, qui voyagent à une vitesse relative constante, voient chacun le temps de l'autre se contracter, ceci conduisant à l'apparent paradoxe que chacun croit que l'autre vieillit moins que lui. Dans un espace fini, les jumeaux peuvent être tous deux sur des orbites périodiques inertielles fermées qui peuvent se croiser, offrant ainsi la possibilité de comparer leurs âges. Comme nous le montrons, il vont bien constater les mêmes âges respectifs, ceci montrant bien qu'il n'y a pas de paradoxe. La solution repose sur le fait que cette topologie d'espace détermine un référentiel préférentiel.

Le paradoxe des jumeaux [ paradoxe de Langevin] s'exprime et se résout simplement dans un espace plat infini [ espace temps de Minkowski]. Un des jumeaux reste sur Terre , alors que l' autre se déplace à vitesse constante dans une fusée vers une planète éloignée, fait demi tour retourne sur Terre. Chaque jumeau croit que l'autre vieillit moins vite, du fait qu'il voit l' horloge associé à son référentiel, battre moins vite que sienne, et le paradoxe est que chacun pense que l'autre est plus jeune au moment des retrouvailles. Le paradoxe se résout du fait que le vaisseau spatial doit ralentir, s'arrêter sur la planète distante, re-décoller, accélérer jusqu'à atteindre une vitesse constante pour retourner sur Terre. On voit bien que le voyageur dans la fusée n'est "pas tout le temps" dans un référentiel "inertiel" et la Relativité Restreinte ( RR), qui dans ce contexte ne s'applique pas "globalement", n'est donc pas en contradiction avec le fait que le voyageur est effectivement plus jeune que son homologue resté sur Terre. Dans un espace compact le paradoxe prend une forme plus complexe. Si le voyageur est sur une orbite périodique, il peut rester sur un référentiel inertiel tout le temps de son voyage dans l'espace compact, sans s'arrêter ou faire demi tour. Comme les deux jumeaux sont dans des référentiels inertiels , chacun devrait voir le temps de l'autre contracté. Le paradoxe vient alors du fait que chacun va croire l'autre plus jeune lorsqu'ils vont se retrouver côte à côte. Nous allons montrer comment le " paradoxe" se résout dans un espace compact et que c'est bien le voyageur qui est effectivement plus jeune. La résolution s'appuie sur l'existence d'un référentiel préférentiel inhérent à cette topologie, dont une des conséquences est l'impossibilité pour le jumeau voyageur dans la fusée de synchroniser correctement son horloge [ 1,2 ]. D'autres auteurs sont déjà arrivés à la même conclusion [ 1- 3 ] , mais nous présentons ici la solution la plus générale, qui ne s'appuie sur aucune topologie particulière. Nous utiliserons le langage moderne de la topologie tel qu'il a été introduit récemment en Cosmologie [4].

[ Quelques rappels utiles: Géométrie et Topologie

La forme globale de l'Univers, incluant ses régions les plus éloignées de nous, est caractérisé par sa Géométrie et sa Topologie. Le terme Géométrie, tel qu'utilisé par les mathématiciens, décrit toutes les caractéristiques locales de l'espace ( courbure, torsion, métrique s'il y en a une, connexions, holonomies, ..), alors que la Topologie décrit les caractéristiques globales qui sont invariantes par des déformations continues réversibles (homéomorphismes) , sans couper ni déchirer l'objet. La Relativité générale est invariante par difféomorphisme (covariance générale) mais pas par homéomorphisme, c'est pourquoi elle ne dit rien sur la Topologie globale de l'Univers qu'elle décrit ( degré de liberté, en général on choisit la topologie simplement connexe, qui est la plus simple). Pour obtenir la solution globale il faut prendre en compte des conditions supplémentaires "topologiques", qui peuvent être connues par des observations par exemple. Des concepts importants en topologie sont d'une part la connexité , qui caractérise le nombre maximum de coupures que l'on peut faire avant de morceler l'objet, une topologie simplement connexe signifie qu'avec une coupure on obtient toujours 2 morceaux, cette connexité est reliée aux nombre de "trous" dans l'objet, d'autre part la compacité qui correspond à un " N-Volume" fini]

La Variété de la Relativité restreinte est (RxM) où R représente la direction du temps et M=R³ est l'espace plat infini 3D. La métrique de l'espace-temps plat est :

ds² = g_mn dx^mdxⁿ avec g^m_n = diag ( -1, 1, 1, 1 ) (1.1) ,

et

| t |

x^m = | x |

| y |

| z |

L'espace temps est invariant sous les transformations du groupe Poincaré [ groupe complet de la RR] qui contient les translations , rotations et les transformations de Lorentz liées aux vitesses relatives uniformes entre référentiels (encore appelées propulsions ou rotations hyperboliques).

Les isométries peuvent être représentées par des matrices O ( 3,1). Nous considérons la Relativité Restreinte dans une variété compacte à trois dimensions:

Mc = (R x M/Γ ). Les éléments Φ de Γ s'appliquent de façon discrète sur l'espace, sans points fixes, et sont un sous ensemble du groupe complet d'isométries. On peut dire que le groupe Γ est l'ensemble des règles ( instructions) permettant de compacifier l'espace. Toutes les topologies plates multiconnexes peuvent être générées à partir soit d'un parallélépipède soit d'un prisme hexagonal en identifiant les côtés opposés conformément aux règles données par les éléments Φ de Γ. [5- 8].

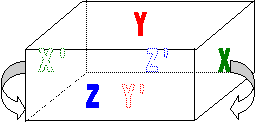
[ Pour construire un hyper-tore de base, on part d'un parallélépipède et en le déformant on vient " coller les trois couples de faces opposées deux à deux ( X sur X' comme indiqué sur la figure ,puis Y sur Y' et Z sur Z' de même, évidemment ce n'est pas facile à se représenter dans un espace 3 D, comment on peut coller les 3 paires de faces simultanément). Signalons que ce n'est pas la seule topologie compacte "plate", il en existe 10 en trois dimensions]

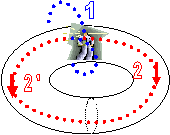
[Commençons par une illustration plus simple. On voit mieux la méthode de construction sur un tore 2 D (on s'intéresse à la surface du tore) : on part d'un rectangle, on identifie une paire de côtés opposés X et X' qu'on vient abouter et "coller" on obtient un cylindre qu'on déforme pour venir abouter et coller l'autre paire de côtés opposés Y et Y' du rectangle initial. Pour un hyper-tore c'est la même chose avec une dimension de plus ].

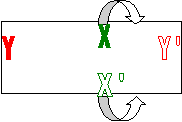
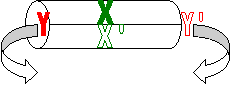
Vision de L'observateur

Dans un espace "Torique, l'observateur voit un nombre infini de copies de lui même de dos ( une par tour de type 1) et de chaque côté ( une par tour de type 2,2')

Il est intéressant d'inclure l'espace temps à (3 + 1 ) dimensions dans un espace temps de Minkowski à (4+1) dimensions avec la coordonnée de quatrième dimension spatiale fixée. [ cela va permettre de définir simplement l'opérateur d'identification ].

En particulier les coordonnées à ( 3 + 1 ) dimensions ( 1.2) sont remplacées par les coordonnées à ( 4 + 1 ) dimensions suivantes.

| t |

| x |

x^a = | y | ( 1.3)

| z |

| q |

où q est fixé à l'unité comme la figure 1 le montre. Les indices grecs sont valorisés de 0 à 3 et les indices latins sont valorisés de 0 à 4

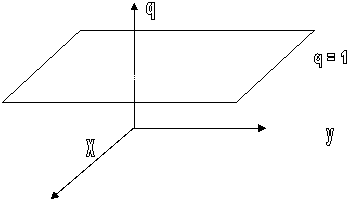
Figure 1: Inclusion d'un espace de Minkowski (3+1) dans un espace de Minkowski (4 + 1) . Les dimensions ( t, z ) ont été supprimées si bien que la Variété est un plan infini positionné à q = 1.

Dans ce système de coordonnées , les générateurs peuvent être représentés par des matrices 5x5. Par exemple le générateur qui opère l'identification d'un point (t,x,y,z,q) avec le point ( t,x+L_x,y,z,q ) peut s'écrire [ 9 ]:

1	0	0	0	0
0	1	0	0	Lx
Tx = 0	0	1	0	0 (1.4)
0	0	0	1	0
0	0	0	0	1

De sorte que la "condition de bord" peut s'exprimer par x -> T_x.x , ce qui se généralise à:

x^a -> Φ^a_b.x^b (1.5)

Pour tout Φ de Γ.

[ Cette condition reflète la topologie compacte et traduit le côté " périodique" des coordonnées : si on traverse ce " bord " (non matérialisé, car pas de point fixe pour la transformation) on retombe sur le même point " de l'espace compact" de la variété ]

A titre d'exemple l' hyper-tore est construit à partir du parallélépipède en collant les faces opposées comme nous l'avons indiqué précédemment.

Les éléments de Γ sont T_x de l'équation ( 1.4) et

1	0	0	0	0
0	1	0	0	0
Ty = 0	0	1	0	Ly
0	0	0	1	0
0	0	0	0	1

1	0	0	0	0
0	1	0	0	0
Tz = 0	0	1	0	0
0	0	0	1	Lz
0	0	0	0	1

Une autre topologie compacte est obtenue à partir du même parallélépipède en effectuant une torsion d'un demi tour sur les faces opposées "z" avant de les identifier ( et coller) . Les éléments de Γ , pour cet espace avec torsion sont T_x , T_y , R_z (π). T_z avec R_z ( θ ), la matrice de rotation ( 1.6):

1	0	0	0	0
0	Cos θ	Sin θ	0	0
Rz (θ) = 0	-Sin θ	Cos θ	0	0
0	0	0	1	0
0	0	0	0	1

Toutes les topologies multi -connexes de géométrie plate, peuvent être construites à partir d'une combinaison de ces translations et de ces rotations.

Les orbites périodiques sont particulièrement intéressantes, car sur elles, un observateur peut rester en situation inertielle [ trajectoires inertielles: on flotte dans l'espace ].

Une orbite périodique peut être décrite par les holonomies Φ de Γ, qui relient le point terminal de l'orbite ( après une période) au point de départ. Autrement dit , une orbite périodique se caractérise par x _fin = Φ. x _départ où Φ peut être un mot composite Φ= Πⁿ_i Φ_ki. Chaque mot a une orbite périodique qui lui correspond. Par exemple, si nous considérons l'orbite périodique décrite sur la figure 2 dans un hyper-tore .

Pour cette orbite particulière, nous avons : x _fin = T_y T²_x. x _départ

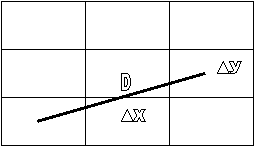
Figure 2. L'hyper-tore compact peut être représenté par un "parallélépipède identifié". On peut également représenter une topologie compacte par un pavage dans l'espace plat infini de Minkowski, par des copies identiques du parallélépipède fondamental . Dans la figure représentée ci dessus, seul le dallage dans les directions ( x, y ) est représenté. On a représenté une orbite D particulière qui correspond à : x _fin = T_y T²_x. x _départ .

[ Ceci correspond à la vision des images multiples qu'un observateur a dans un univers de ce type. Il se voit de dos un nombre infini de fois, une copie par tour et également de chaque côté un nombre infini de fois, une copie par tour à droite et à gauche, comme dans un jeu de miroirs. On voit qu'on peut donc "développer" sa vision des choses en répétant à l'infini et dans toutes les directions de l'espace le"parallélépipède générateur", créant un réseau virtuel de mailles identiques. Cet espace infini, dans lequel l'espace compact est développé s'appelle la couverture universelle. On va avoir à procéder à une " identification" des points dans cet espace de couverture universelle pour associer tous ceux qui correspondent aux mêmes points de l'espace compact. ].

Supposons que l'espace soit compacifié de telle sorte que pour un observateur S, seulement les points d'espace soient identifiés.

[ Insistons sur le fait qu’on suppose que cela est possible, pour une classe d’observateurs donnée, (on imagine, sans le dire qu’il s’agit de ceux au « repos » par rapport à l’espace compact, en effet dans ce cas seulement la ligne d’univers n’est pas périodique, alors que dans le cas d’observateurs « en mouvement » la ligne d’univers étant périodique on devra aussi « identifier » le temps : au bout du temps égal à la période, le phénomène se reproduit identiquement à lui même , comme pour l’espace on considérera que c’est le même point temporel, donc ici on compacifie l’espace temps complet, puisque on identifie les coordonnées complètes d’espace et de temps). Ne suppose t’on pas déjà implicitement l’existence d’un référentiel privilégié, ce qui parait d’ailleurs naturel compte tenu des symétries particulières?]

Dans le système de coordonnées au repos par rapport à S , toutes les holonomies sont telles que Φ⁰_a = 1.

[Ce point important, va être exploité en 1.10, le vecteur colonne (t,x,y,z) va se transformer en le vecteur colonne ( t, Φ^x_ixⁱ ) avec i = 1 à 4]

Le jumeau de S, H, navigue dans un vaisseau spatial dans cet espace compact, toujours à vitesse constante, sans jamais faire demi tour , accélérer ou ralentir (Figure 3). Un système de coordonnées ' au repos par rapport à H sera tel que x' = Λ.x avec la transformation de Lorentz Λ. En (4 + 1 ) dimensions , la transformation de Lorentz la plus générale s'écrit:

γ	γβx	γβy	γβz	0
- γβx	1 + [(γ-1)β²x]/β²	[( γ - 1) βxβy]/β²	[( γ - 1) βxβz]/β²	0
Λ = - γβy	[( γ - 1) βxβy]/β²	1 + [(γ-1)β²y]/β²	[( γ - 1) βyβz]/β²	0
-γβz	[( γ - 1) βxβz]/β²	[( γ - 1) βyβz]/β²	1 + [(γ-1)β²z]/β²	0
0	0	0	0	1

Où les β_i sont les vitesses des propulsions dans les directions ( x, y, z, q ), β²=Σ_i β_i ² et γ² =1/ (1-β²).

La vitesse dans la direction "q" est supposée nulle.[ on a posé "c" =1 comme de coutume.]

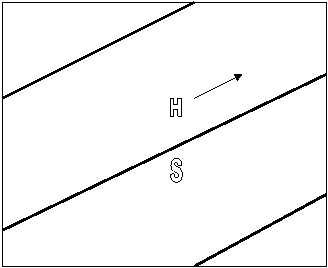
Figure 3 : S reste sur "Terre" pendant que H voyage sur l'orbite périodique de la figure 2.

S voit H parcourir une distance D avant qu'il repasse à son niveau. Pendant cette période, pour S il s'est écoulé :

Δ t = D / β ( 1.7 )

Comme S croît que l'horloge t' de H bat plus lentement d'un facteur:

Δt' = Δt / γ ( 1.8 )

Donc il suppose que pour H il s'est écoulé un temps

Δt' = D / γβ (1.9 )

H serait donc plus jeune que S au moment où leurs trajectoires se croisent.

Il n'y aura pas de paradoxe , si H constate également qu'il est plus jeune que son jumeau. Pour H , et les points d'espace et les points du temps ont été identifiés. Cela implique qu'il est impossible pour H de synchroniser les horloges [ de son référentiel] [1]

H doit être sur une orbite périodique pour rester "inertiel". Supposons que H soit une orbite correspondant au mot composite Φ, donc la condition de bord (1.5) devient x' = Λx ->ΛΦx.

Le défaut de synchronisme va être donné par la composante temporelle de Λ (1 - Φ ).x, soit explicitement en utilisant la transformation de Lorentz sus mentionnée:

δt' = (γt - γβⁱ x_i) - (γt - γβⁱΦ^j_i x_j )

= - γβⁱ ( x_i - Φ^j_i.x_j) (1.10)

avec i = 1,2,3,4 et le vecteur β_i = ( β_x, β_y, β_z, 0 )*, tandis que x_i = ( x, y, z, q ). La distance parcourue mesurée par S est D² =Δx^aΔx_a

[ C'est la définition de la distance dans un espace quelconque ],

soit:

D² = [( x_i - Φ^j_i x_j ) ( xⁱ - Φⁱ_j x^j)] ( 1.11 )

Et

( x_i - Φ ^j_i x_j ) = Dβ_i /β ( 1.12 )

[ = Δt .β_i: distance parcourue sur la coordonnée x_i , D/β = Δt]

Ce qui fait que l'horloge de H présente un défaut de synchronisation par un facteur de :

δt' = - γβD (1.13)

[ on substitue à ( x_i - Φ ^j_i x_j ) sa valeur de (1.12) dans (1.10): δt' = - γβⁱβ_i .D /β =- γβD ]

H voit son jumeau S s'éloigner de lui dans la direction opposée et revenir seulement après avoir parcouru une distance γD.

Avec le décalage additionnel temporel de l'équation ( 1.13 ) du à la topologie compacte, l'horloge de H doit indiquer:

Δt' = γD / β - γβD = D / ( γβ ) ( 1.14 )

en parfait accord avec ( 1.9 ). Les deux jumeaux constatent que H est plus jeune que S. [ 10 ]

Au final, remarquons que la différence d'age entre les deux jumeaux ne dépend pas de la topologie, mais seulement de la distance D. Pour l'orbite de la figure 2, par exemple Φ=T_y.T²_x et l'équation ( 1. 11) donne D² = [(2L_x )²+ L²_y].**

On peut considérer l'exemple précédent de manière moins abstraite et plus physique. Ce que le formalisme précédent montre, c'est qu'un seul référentiel peut être au repos par rapport aux sections spatiales compactes. Tous les autres observateurs inertiels en mouvement relatif vivent dans des univers où à la fois l'espace et le temps sont identifiés. Dans l'exemple donné s'appuyant sur les équations ( 1.7 ) - (1.14 ), le jumeau S est au repos dans un tore de géométrie plate et H se déplace sur une orbite périodique inertielle. Supposons que H ne sache pas que l'espace temps est compact. Pour réaliser correctement des expériences, H doit "baliser"son référentiel en espace et en temps. Il peut déployer une "armée" d'observateurs qui vont par exemple synchroniser leurs horloges en échangeant des signaux lumineux. Quelque part, sur son chemin, H va recevoir son propre message lui indiquent de re-synchroniser son horloge de la valeur γβD. Il va être désynchronisé dans sa propre procédure de tentative de synchronisation. Ceci va impliquer que des observateurs au même point d'espace temps vont avoir des horloges qui indiquent des temps différents. H va se rendre compte que toutes les expériences réalisées dans ce référentiel, seront entachées d'une ambiguïté de temps de la valeur du glissement temporel.

Le paradoxe des jumeaux montre qu'une topologie compacte génère un référentiel préférentiel, nommément celui où la longueur le long d'un côté donné est la plus petite, point qui est souligné en référence [ 1 ] ( voir aussi référence [ 2 ]) . Pour généraliser l'effet aux espaces courbes, Λ doit être remplacé par le difféomorphisme approprié et la topologie généralisée à M_c = R x M^u /Γ, où la couverture universelle M^u est une variété courbe simplement connexe.

Les Cosmologies multi- connexes, battent en brèche le principe Copernicien ( pas d'endroit privilégié dans l'Univers).

Une topologie compacte possède un endroit préférentiel, et un temps préférentiel ce qui fait qu'une galaxie, si ce n'est la nôtre, est au centre de l'Univers. Seuls certains observateurs sont capables de synchroniser leurs horloges et observent un volume minimal pour l'Univers.

Nous remercions P. Ferreira, N.J Cornish, W. T Gowers, A. Kent, R. Jones, G. Starkman et J. Weeks pour nos discussions. JL est reconnaissante au groupe de physique théorique de l'Imperial College de leur hospitalité. J.L est soutenue par PPARC.

Références citées en anglais :

Cf article original

[* Le texte original comporte une coquille de notation, au niveau de la position des indices ( sans conséquences en espace temps plat, mais j'ai mis tous ces indices bas, pour être homogène)

** Le texte original indique D² = (2L²_x+ L²_y), mais je pense que c'est une coquille ].