Original ( en anglais) par Michael Weiss http://math.ucr.edu/home/baez/physics/Relativity/SR/TwinParadox/twin_paradox.html

Traduction par J. Fric qui endosse toute la responsabilité sur les âneries et autres incongruités que sa traduction aurait pu introduire, commentaires personnels en bleu entre […]

Le Paradoxe de Langevin:

Avertissement

La Relativité est un sujet qui par ses prédictions stupéfiantes prend parfois un tour passionnel. Elle a ses défenseurs (majoritaires dans la communauté scientifique) qui la soutiennent avec ardeur et ses détracteurs qui la dénoncent avec ténacité. Le document ci après ne convaincra donc pas grand monde à part peut être quelques indécis qui se seraient égarés sur le net.

Toutefois nous estimons de notre devoir de signaler que ce document développe scientifiquement, mais non sans une certaine gourmandise, quelques aspects de la théorie qui sont particulièrement troublants. Certains passages risquent donc de hérisser quelques susceptibilités qui seraient allergiques à cette théorie. Nous leur en déconseillons donc vivement la lecture qui de toute façon ne les convertirait pas.

Introduction

Dans nos histoires de jumeaux, ils sont parfois lapidairement appelés A et B. Nous préférons les appeler Stella et Terence. Terence reste à la maison sur terre. Stella vole au loin dans un vaisseau spatial à presque à la vitesse de la lumière, fait demi tour après un moment, et puis comme Ulysse plein d'usage et raison retourne auprès de ses parents finir le reste de son age. (ainsi Terence est le Terrien alors que Stella est dans les étoiles.)

Quand nos héros se retrouvent quel dilemme ! Le temps a-t-il ralenti pour Stella, qui a voyagé ou est ce l'inverse. La symétrie des équation de la RR ne nous renseigne pas de façon évidente.

Pour ne pas maintenir trop longtemps le suspense, disons que la RR opte sans équivoque pour la première réponse: Stella vieillit moins que Terence entre le départ et les retrouvailles.

Tordons le cou à l'argument "c'est la terre qui se déplace par rapport à Stella" La RR ne déclare pas que tous les référentiels sont équivalents, seulement les référentiels inertiels. Le référentiel de Stella n'est pas inertiel quand elle accélère. Et c'est discernable car Stella a dû mettre le feu à ses moteurs à mi-chemin de son voyage; Terence n'a fait rien de la sorte. Le vase Ming qu'elle avait emprunté à Terence, qui flottait dans le vaisseau spatial est tombé quand elle a allumé ses moteurs, et il est s'est brisé [ Terence a bien regretté d'avoir prêté son vase à Stella]. Elle a lutté pour maintenir son équilibre, comme l'équipage de Star Treck. En bref, elle a senti l'accélération, alors que Terence ne sentait rien.

Super! En un petit paragraphe , nous avons résolu, le paradoxe de Langevin. Est-ce bien sûr? Bien, pas tout à fait. Il n'y a rien de faux dans ce que nous avons dit jusqu'ici, mais nous avons omis beaucoup de choses. Ce sont les raisons de la confusion habituelle.

Pour une chose, nous avons été plutôt injustes à Stella. Nous avons dit pourquoi elle ne peut pas simplement adopter le point de vue de Terence, mais nous n'avons pas dit comment elle voit les choses de son point de vue. Il paraît étrange que Terence puisse vieillir de plusieurs années juste parce que Stella allume ses moteurs. Les objections de la discontinuité temporelle et la dépendance de la distance éclairent cet aspect délicat des choses.

Il y a des versions du paradoxe de Langevin où Stella n'allume pas ses moteurs et ne sent aucune accélération (la variante de Slingshot, où Stella orbite autour d'une étoile éloignée en trajectoire inertielle, et la variante de Magellan, où Stella voyage autour d'un univers cylindrique ou sphérique). Ces cas jettent un doute sur le rôle de l'accélération dans la version habituelle. (nous pourrons ajouter des entrées de FAQ pour ces variantes dans l'avenir, mais pour l'instant ils sont laissés en tant qu' exercices pour le lecteur.)

Enfin et la relativité générale (RG) dans tout cela? Est ce que Stella ne peut pas prétendre qu'elle est immobile tout le temps, et qu'un champ de la gravité homogène s'est juste établi dans l'Univers quand elle a mis en marche ses moteurs? (Rappelons que Terence subit la pesanteur de la terre, son référentiel est il vraiment inertiel?) Certains soutiennent que le paradoxe de Langevin ne peut être résolu que dans le cadre de la RG. Nous sommes en désaccord, mais l'explication de la RG du Paradoxe de Langevin éclaire utilement certains points. Le point de vue de RG est presque obligatoire pour comprendre certaines des variantes du paradoxe de Langevin.

Nous présentons "une version standard" du paradoxe en détail, et établissons une certaine terminologie. Pour simplifier, nous ne traitons pas l'accélération de Stella au début et à la fin du voyage (cela ne change rien à la validité de la démonstration). Nous supposons que Stella passe en flèche dans son vaisseau spatial, à côté de Terence les deux fois (on se demande comment elle a fait pour emprunter son vase Ming à Terence).

Voici l'itinéraire selon Terence.-

Début

Stella passe en trombe à côté de moi. Nos chronomètres sont synchronisées à 0.

Trajet aller

Stella croise à (disons) presque 99 % de la vitesse de la lumière. À 99%, le facteur de dilatation de temps est d'un peu plus de 7, ainsi disons que la vitesse est juste un poil en dessous de 99% et que le facteur de dilatation de temps est exactement de 7. Disons que cette partie du voyage dure 7 ans (selon Terence, naturellement).

Demi tour

Stella met le feu à ses moteurs pendant par exemple 1 jour pour inverser le mouvement, jusqu'à ce qu'elle croise en arrière vers la terre à presque 99% de vitesse de la lumière. (Stella est robuste.) Quelques variantes sur le paradoxe réclament un demi tour instantané. Nous appellerons cela l'événement de demi tour.

Trajet retour

Stella croise vers la terre pendant 7 années à 99% de la vitesse de la lumière.

Fin ( Retour)

Stella passe en trombe près de Terence dans l'autre direction, et ils comparent leurs chronomètres, leurs cheveux gris, ou n'importe quel autre signe de temps écoulé.

Selon Terence, 14 ans et un jour se sont écoulés entre le début et le retour.

Le chronomètre de Stella n'indique qu'à peine plus que 2 ans.

Combien de plus? Bien, Terence indique que le demi tour a pris un jour. La vitesse de Stella changeait tout au long du demi tour, donc son facteur de dilatation de temps, qui changeait entre 1 et 7. Ainsi la mesure de Stella du temps de demi tour sera quelque chose entre 1 jour et un septième d'un jour. En regardant de plus près, elle s'avère être un peu plus de 15 heures.

Le Paradoxe de Langevin: L'Explication par l'Effet Doppler

Concentrons nous sur ce que Stella et Terence voient réellement, de leurs propres yeux. Juste pour souligner que nous parlons de l'observation directe ici, je mettrai le verbe "voir" et ses équivalents en gras dans toute cette section.) Pour rendre les choses intéressantes, nous les équiperons des télescopes incroyablement puissants, ainsi chaque jumeau peut observer l'autre horloge pendant tout le voyage. Si chacun des jumeaux a vu l' horloge de l'autre retarder pendant tout le voyage, alors nous avons une contradiction. Mais n'est pas ce qu'ils voient.

[ NB : Ajoutons également que vu l'effet "Doppler " leurs images sont très décalées soit vers le rouge soit vers le bleu et qu'en fait il ne verraient rien, si nous ne les avions pas muni d'un ingénieux dispositif de réception qui réalise la transposition adéquate dans le visible ]

Pour le cas où il serait trop difficile de lire l'horloge par le télescope, nous ajouterons un équipement lumineux à chaque horloge, réglé pour émettre un éclair par seconde. Nous sommes tenté de supposer que Terence voit l'horloge de Stella clignoter une fois que toutes les 7 secondes (avec le facteur de dilatation de temps où nous avons choisi) et vice versa [ainsi chacun voit l’horloge de l’autre, et évidemment dispose de sa propre horloge, ce qui permet les comparaisons].

Que nenni! Sur la Trajet aller, Terence voit approximativement un éclair toutes les 14 secondes, sur la Trajet retour, il voit son horloge clignoter à environ 14 éclairs par seconde. C'est-à-dire, il la voit avancer. Stella voit le même comportement vis à vis de l'horloge de Terence.

Quid de cela? Bien, le titre de section l'indique: remplacez juste les mots "éclairs par seconde" par des "cycles par seconde", et vous identifierez l'effet Doppler qui vous est Familier. Les impulsions régulières sont décalées vers le rouge (vers de plus basses fréquences et les impulsions sont élargies) pendant la Trajet aller, et décalées vers le bleu ( vers des fréquences plus élevées et les impulsions raccourcies) pendant le Trajet retour.

Les facteurs d'effet Doppler que j'ai donnés (1/14 et 14/1) sont issus de la formule relativiste de l'effet Doppler. La formule relativiste tient compte et du retard lié à la distance de la formule non-relativiste, et de la dilatation relativiste de temps. En d'autres termes, Terence calcule que l'horloge de Stella bat 7 fois moins vite tout le temps, mais il la voit fonctionner plus rapidement pendant la Trajet retour parce que chaque éclair a une distance plus courte à parcourir. Et Stella calcule la même chose pour Terence.

Très bien , mais tout ceci ne semble que contribuer à durcir le paradoxe! Stella voit ce que Terence voit : une horloge qui musarde sur le trajet aller et une horloge qui essaie de rattraper le temps perdu sur le trajet retour. D'où vient l'asymétrie entre Stella et Terence?

Réponse: Dans la longueur des trajets d'arrivée et de départ , tels qu'ils sont vus . Pour Stella, chaque trajet prend environ une année. Terence maintient que le demi tour de Stella a lieu à l'année 7 à une distance de presque 7 années-lumière, ainsi il ne pourra pas la revoir avant l'année 14. Mais Terence voit un Trajet aller long et un Trajet retour très court.

C'est là, l'asymétrie fondamentale: le passage du déplacement vers le rouge au déplacement vers le bleu se produit au demi tour de Stella. Stella voit à travers le télescope Terence vieillir lentement sur son Trajet aller, mais l'accélération du vieillissement de Terence observé sur l'image qu'elle reçoit sur le trajet retour compense davantage sa flânerie sur le Trajet aller. Terence voit l'image de Stella vieillir lentement aussi au début , mais la phase de vieillissement rapide vient trop tard pour gagner la course.

[Pour bien comprendre cela il faut se référer au diagramme de la figure 2. Il est clair que quand Terence voit Stella faire demi tour (ce qui est visualisé par la flèche rouge qui représente le trajet de la lumière à 45° vers la gauche, qui part du point de demi tour et aboutit sur l’axe des temps qui est le référentiel de Terence), pratiquement tout le temps s’est écoulé pour lui (Il a vu Stella vivre au Ralenti d’un facteur 14 environ, comme prévu quand elle s’éloigne). Donc même s’il voit en accéléré le «  retour », d’un facteur 14, c’est trop tard.

A noter sur que le diagramme on a représenté un facteur de dilatation du temps de 2 (pour qu’il soit lisible, avec 7 on ne verrait rien, les traits représentant les trajets de la lumières, seraient sur ceux de la ligne d’Univers de Stella).

Pour Stella c’est différent, au demi tour, un an s’est écoulée pour elle, mais elle voit que peu de temps s’est écoulé pour Terence comme prévu ( elle le voit aussi vivre au ralenti) , mais pendant l’année de son retour elle va voir Terence vivre en accéléré d’un facteur de l’ordre de 14, ce qui explique le résultat.

Ce diagramme montre bien la dissymétrie (cachée) de la situation, selon le sens de propagation de la lumière (de Stella vers Terence, ou l’inverse). Bien sûr, le fait que l’un voit l’autre vivre en accéléré ou au ralenti, ne veut pas dire qu’il vive en accéléré ou au ralenti. Le temps propre vécu et marqué par sa propre Horloge s’écoule imperturbablement à son rythme régulier (et pour cause c’est lui sa propre référence. En fait, dire que le temps ralentit ou accélère est une pure absurdité. Ce qui est en jeu ici, c’est que les temps propres de Stella et Terence entre deux points communs de l’espace temps, c’est à dire aux points d’intersection de leurs deux lignes d’univers s’est écoulé différemment. C’est cela le concept essentiel en Relativité Restreinte qu’il faut bien comprendre. Si ceci paraît paradoxal, dans les situations habituelles, c’est que cet écart est si petit qu’il n’est pas notable, mais si les vitesses relatives sont grandes, ce n’est plus le cas. A noter que, bien entendu, le fait que Terence et Stella vivent des temps propres différents ( vieillissent différemment) ne viole en rien les lois physiques et le critère de causalité compte tenu de la limite imposée par la vitesse de la lumière.

Ce ralentissement ou accélération n’est qu’un « effet de perspective ». Mais ce qui est fondamental dans l’expérience c’est que toutes les impulsions émises par l’horloge de Stella entre le moment où ils se croisent (au départ) et le moment où il se recroisent (à l’arrivée) ont été reçues par Terence, dans l’ordre d’émission, même si leur rythme a été perturbé, et réciproquement. C’est un point à bien comprendre également pour comprendre la validité de l’expérience]

Le Paradoxe de Langevin: L'Explication par le Diagramme d'espace Temps

Ce paragraphe emprunte fortement à l'entrée originale de FAQ pour le paradoxe de Langevin, par Kurt Sonnemnoser. Cependant, elle également a été largement modifiée, ainsi il n'est responsable en aucun cas des imprécisions ou maladresses du document.

Minkowski dit, "dorénavant espace seul, et temps seul, sont condamnés se réduire à de simples ombres, et seulement un genre d'union des deux en préservera une Réalité indépendante." Minkowski a projeté la version de la Relativité Restreinte d'Einstein dans un nouveau cadre, l'espace temps de Minkowski. Le paradoxe de Langevin a une résolution très simple dans ce cadre. Le concept crucial est le temps propre d'un corps mobile.

Choisissons d'abord un référentiel inertiel de référence, disons le référentiel repos de la terre (que nous supposerons inertiel, même si ce n'est pas vrai: les puristes ont le droit d'imaginer que Terence est dans l'espace dans une station si éloignée de tout que …). Une fois que nous avons choisi un référentiel de référence, nous pouvons définir les coordonnées ( t, x, y, z) pour chaque événement qui a lieu. On nous demande d'imaginer une armée d'observateurs, tous équipés d' horloges et de règles, et tous au repos par rapport au référentiel de référence. Avec leurs horloges et règles ils peuvent déterminer quand et où n'importe quel événement a eu lieu , en d'autres termes, ses coordonnées ( t, x, y, z) . Dans un référentiel différent de la référence, une armée différente d' observateurs déterminerait différentes coordonnées pour le même événement. Mais nous en tiendrons à un référentiel dans toute cette discussion.

L'ensemble de tous les points-événements spatiaux-temporels, s'appelle l'espace temps.

Traditionnellement, on trace des événements dans l' Espace-temps sur un diagramme Espace-temps de Minkowski. C'est juste un morceau de papier (ou de tableau noir!) avec la Coordonnée "t" tracée verticalement vers le haut, et la Coordonnée "x" tracée horizontalement. (on ignore souverainement les coordonnées y et z, le papier et les tableaux noirs en 4 dimensions étant difficiles à obtenir dans la plupart des universités.)

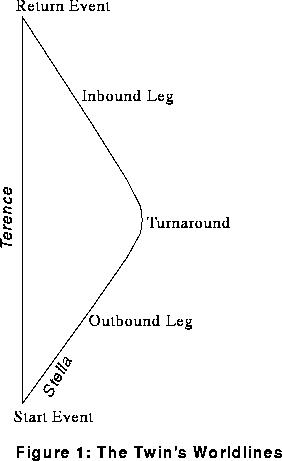
Si nous traçons tous les événements de Terence et de Stella, nous obtenons ce que nous appellerons leurs lignes d'univers. (A noter: le physicien George Gamow a intitulé son autobiographie, "Ma ligne d'univers".) Les lignes d'univers de Terence et de Stella sont montrées sur la figure 1

.

Puisque Terence est au repos dans notre référentiel choisi comme référence, à tout moment il sera au le même endroit, disons (0.0.0). En d'autres termes, les coordonnées de ses événements prennent toutes la forme: (t,0,0,0)

Mais à un temps arbitraire, les coordonnées évènementielles de Stella vont prendre la forme:

( t, f(t), g(t), h(t))

Où, f (t), g (t), et h (t) sont toutes des fonctions de t , et t (rappelez-vous) est mesuré par un certain quidam dans notre armée d'observateurs.

La traçage de la distance fonction du temps est un jeu d'enfant. La métrique de Minkowski est décrite par la formule suivante:

ds² = dt ² = dt² -dx²-dy²-dz²

Ici, dx , dy , et dz sont toutes les différences de coordonnées entre deux événements qui sont proches sur le diagramme de Minkowski. Ainsi si ( t, x, y, z) sont coordonnées d'un événement, alors ( t+dt, x+dx, y+dy, z+dz ) sont coordonnées de l'autre. Le temps et l'espace sont mesurés dans les unités pour lesquelles c, la vitesse de la lumière, est égale à 1 (par exemple, des secondes pour le temps et des seconde-lumière pour la distance). Et dt , est finalement la différence de temps propre, que nous définissons après.

Si on considère quelqu'un, portant une montre, se déplaçant uniformément de l'événement ( t, x, y, z) à l'événement ( t+dt, x+dx, y+dy, z+dz ). Le temps entre ces deux événements, mesuré par la montre de cette personne , s'appelle le temps propre écoulé pour cette personne. Et selon Minkowski, le temps propre est donné par dt dans la formule ci-dessus.

Plus généralement, supposez quelqu'un muni d'une montre de précision voyage sur une ligne d'univers de l'événement E à l'événement F. "de précision" signifie ici que l'accélération n'affecte pas le mécanisme générant le temps. Une horloge à balancier ne serait pas un bon choix! Une horloge atomique est le meilleur choix. Combien de temps s'écoule t'il selon la montre?, c.à.d., quel est le temps propre sur cette ligne d'univers entre les événements E et F? C'est simple, intégrez simplement dt :

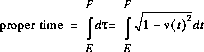
où

est le vecteur de vitesse, et [ v (t) ]² est le carré de sa longueur:

[ v(t)]² = (dx/dt)² + (dy/dt)² + ( dz/dt)²

Vous ne devriez pas avoir beaucoup de difficulté obtenir ces formules à partir de ce que nous avons déjà dit.

En général, il est difficile évaluer notre intégrale pendant le temps approprié, mais certains cas spéciaux sont bibliques. Prenons le cas de Terence d'abord. Rappelez-vous que ses coordonnées d'événements sont toujours ( t , 0, 0, 0), ainsi dx , dy , et dz sont toujours nuls pour lui. Ainsi dt = dt , et l'intégrale devient:

C'est-à-dire, juste la différence de la Coordonnée "t"! En d'autres termes, le temps propre écoulé de Terence est juste le temps propre écoulé mesuré par notre armée d'observateurs, dans le référentiel de référence dans lequel Terence est au repos. De là à supposer que Terence est un de ces observateurs, il n'y a qu'un pas.

Maintenant qu'en est il de Stella? Pour elle, les dx , dy , et dz ne sont pas toujours nuls. Donc dx/dt , dy/dt , et dz/dt ne sont également pas toujours nuls, et leurs carrés (qui apparaissent dans la formule pour [ v (t) ]²) sont toujours non négatifs, et parfois positifs Ainsi la quantité sous la racine carrée est inférieure ou égale à 1, et parfois strictement inférieure à 1. Conclusion: la valeur de l'intégrale de Stella est inférieure à celle de l'intégrale de Terence. C.-à-d., son temps propre écoulé est inférieur à celui de Terence. C.-à-d., elle vieillit moins.

Voilà toute l'histoire! Nous évaluons une intégrale de chemin [donnant le temps propre] le long de deux chemins différents, et nous obtenons deux résultats différents.

Le Paradoxe de Langevin: L'Explication de la "Relativité Générale"

Appeler ceci "l'explication générale de relativité" donne des boutons à certains. Je dirai pourquoi ci-dessous . C'est pourquoi les termes "Relativité générale"(RG) et gravitation sont entre guillemets ( les "guillemets de l'épouvante") dans ce chapitre..[à noter que l’auteur s’est lâché et a manifestement pris son pied dans ce chapitre]

Quelques rappels de base

Cette explication se fonde sur quelques affirmations qui sont vraies, selon la RG. (nous différons l'examen de ce que la RR dit au sujet de ces affirmations.)

· Libre choix des référentiels de référence: Vous pouvez décrire la physique d'une situation depuis n'importe quel référentiel à votre guise, mais quelques référentiels exigent l'introduction des champs de force qui n'apparaissent pas dans d'autres référentiels. Vous pouvez les appeler "champs de pseudo-force", ou même "champs de gravitation".

· Dilatation uniforme "gravitationnelle" de temps: Si vous avez deux horloges identiques . On place l'une au fond d'un puits de potentiel "de gravitation" uniforme (ou puits "pseudo-potentiel" , si vous préférez) et on place l'autre plus haut. Si les deux horloges comparent leurs rythmes en envoyant les signaux lumineux dans les deux sens, alors toutes les deux conviendront que l'horloge inférieure bat plus lentement que l'horloge supérieure.

J'ai exprimé ces conditions aussi soigneusement que possible, sans recours aux mathématiques formelles. De façon plus lapidaire, on dit, "vous pouvez employer les référentiels accélérés comme référence, à condition d'y inclure des champs de pseudo forces et les horloges battront de plus en plus lentement au fur et à mesure que vous descendrez dans le puit de potentiel associé au champ uniforme de pseudo-force."

Des livres plus anciens ont appelé notre première affirmation le principe général de la relativité, mais ce terme est tombé en désuétude. Elle peut vous rappeler le principe d''équivalence, mais c'est vraiment quelque chose de différent. La version lapidaire indique que vous ne pouvez pas distinguer un champ de gravitation dû à la matière d'un champ de pseudo-force. Nous n'aurons pas besoin du principe d'équivalence ici, ainsi je ne fatiguerai pas à en faire une description rigoureuse. Néanmoins, vous pouvez voir probablement les liens qui s'y réfèrent.

Sans principe d'équivalence, la dilatation uniforme "gravitationnelle " du temps n'a rien à voir avec la pesanteur. (appelez la "dilatation du temps de pseudo-force" à la place.)

OK, maintenant pour le paradoxe de Langevin

Notre version habituelle , est celle ci. Nous sélectionnerons le référentiel dans lequel Stella est, et nous le déclarerons au repos, tout le temps! Quand elle met à feu ses moteurs pour le demi tour, elle est forcée de supposer qu'un champ "de gravitation" uniforme inonde soudainement tout l'univers : le champ compense exactement la force de ses moteurs, ainsi elle reste immobile [ ce champ est uniforme dans tout l’univers, étant de nature cinématique, car quelle que soit la distance de l’objet, Stella, qui se suppose immobile, le voit animé de la même « accélération », ce qui suppose un champ de gravitation fictif uniforme, ce qui est évidemment différent des champs réels de gravitation qui décroissent avec la distance].

Pas pour Terence. Le champ cause son accélération, (du point de vue de Stella qui le voyait s'éloigner régulièrement et qui voit maintenant sa vitesse d'éloignement ralentir, s'inverser et puis qui voit Terence se rapprocher en tombant vers elle en chute libre, comme un projectile tiré verticalement dans un champ de pesanteur), mais Terence ne sent rien puisqu'il est en chute libre (ou plutôt la terre dans son ensemble l'est). Il y a une énorme différence de potentiel entre lui et Stella: rappelez-vous, il est à des années-lumière de Stella, dans un champ de gravitation uniforme! Stella au fond du puit de potentiel, il est au "sommet" (ou le serait si le puit n'était pas sans sommet). Ainsi par la dilatation uniforme "gravitationnelle" du temps, il vieillit de plusieurs années pendant le demi tour de Stella.

Maintenant que vous avez compris le principe, relax, calez vous confortablement dans votre fauteuil et enfilez vos Charentaises. Car il y a un bonus: L'explication de la RG règle son compte aux objections "de la discontinuité temporelle" et de la " dépendance de la distance".

L'objection de la "discontinuité temporelle", nous invite à considérer la limite d'un demi tour instantané. Mais dans cette limite le champ gravitationnel devient infini entraînant une dilatation temporelle infinie. Ainsi Terence « vieillirait » [ Rappel : cf l’explication par l’effet Doppler, Terence ne vieillit pas « physiquement » irrégulièrement, mais imperturbablement à son rythme, cet effet de modulation du vieillissement tient au fait que le référentiel dans lequel il s’évalue change continûment pendant l’accélération] de plusieurs années instantanément, ce qui est physiquement irréaliste, comme un demi tour instantané.

L'objection de " dépendance de la distance" stipule qu'il est curieux que le « vieillissement » de Terence dépende de sa distance à Stella quand elle fait son demi tour, et non pas seulement du temps du demi tour tel que mesuré par Stella. Pas de mystère, la dilation temporelle dépend de la différence de potentiel "gravitationnel", qui dépend de la distance (dans un champ uniforme)

Vous pouvez être intrigué par la grande coïncidence: comment se fait-il que le champ "de gravitation" uniforme surgit juste au moment ou Stella allume ses moteurs? Vous pourriez aussi bien demander à des enfants sur un manège pourquoi la force centrifuge apparaît soudainement quand l'opérateur du manège met en marche le moteur. Il y a une raison pour que de telles forces aient dû supporter le préfixe infâmant"pseudo" dans tant de livres.

Vous pouvez trouver la dilatation uniforme "gravitationnelle" du temps, la deuxième affirmation, un peu trop commode. D'où vient elle? Est-il juste un facteur ad hoc introduit par Einstein pour résoudre le paradoxe de Langevin? Pas du tout. Einstein a donné quelques arguments pour cela, n'ayant rien à voir avec le paradoxe de Langevin. Ces arguments n'ont pas besoin du principe de l'équivalence. Je ne répéterai pas les arguments d'Einstein (recherchez ci après, quelques références si vous êtes curieux), mais j'en dirai davantage au sujet de cet effet dans la section " trop d'explications"

La dilatation gravitationnelle du temps (sans guillemets d'épouvante) (c.à.d., champs dus à la matière) est une histoire différente. Ces champs ne sont jamais uniformes, et les arguments mentionnés ne fonctionnent pas. L'essence du premier traité d'Einstein de la relativité générale était ceci:

(a) Un champ de gravitation uniforme entraine une dilatation du temps.

(b) le principe d'équivalence implique alors la dilatation du temps pour les champs de gravitation (sans guillemets d'épouvante).

Une œuvre magistrale, mais non pertinente dans le paradoxe de Langevin.

Qu'est ce que la relativité générale ( en bref)?

Einstein a travaillé à l'incorporation de la gravitation dans la théorie de relativité de 1907 à 1915; En 1915, la relativité générale avait atteint une forme très proche de sa forme moderne. (Oh, les mathématiciens ont trouvé quelques points à peaufiner et à recouvrir de plaqué or, mais les bases conceptuelles demeurent les mêmes.) Si vous lui demandiez d'énumérer les dispositifs cruciaux de la relativité générale en 1907, et encore en 1915, vous obtiendriez probablement les listes très différentes. Les physiciens modernes ont une liste différente de la liste d'Einstein 1907.

Voici ma version de la liste d'Einstein 1907 (sans s'inquiéter trop des détails):

Principe général de relativité

Tout mouvement est relatif, pas seulement les mouvements uniformes. Toutefois, vous devrez inclure de prétendues pseudo-forces, (comme la force centrifuge ou la force de Coriolis).

Principe d'équivalence

La pesanteur n'est pas essentiellement différente d'une pseudo-force.

Le principe général de la relativité joue un rôle primordial dans l'explication par la "RG" du paradoxe de Langevin. Et ce principe a donné à relativité générale son nom. Donc il y a certainement justification historique pour le terme "explication par la RG". Même en 1916, Einstein a continué à choisir le principe général de la relativité comme dispositif central de la nouvelle théorie. (voyez par exemple les trois premières sections de son papier 1916, "la base de la théorie générale de relativité", ou sa célèbre présentation de la relativité.

Voici la liste du physicien moderne (encore, sans pinaillage excessif):

Structure d' Espace-temps

Espace-temps est une Variété Riemannienne à 4-dimensions. Si vous voulez l'étudier avec des coordonnées, vous pouvez employer n'importe quel ensemble de système de coordonnées régulières, (ce libre choix est ce qui est advenu du principe général de la relativité.)

Principe d'équivalence

Le métrique du Espace-temps induit une métrique de Minkowski sur les espaces tangents. En d'autres termes, à une approximation de premier ordre, un petit domaine de l'Espace-temps ressemble à un petit domaine de l'Espace-temps de Minkowski. La chute libre des corps suit une géodésique.

Attraction universelle = Courbure

Un champ de la gravitation dû à la matière correspond à une courbure de l' Espace-temps. En d'autres termes, une fois que nous soustrayons de la référence, les effets du premier ordre en employant une référentiel chute libre, les effets de second ordre restants trahissent la présence du champ de la gravité (vrai).

Le troisième dispositif trouve sa expression mathématique précise dans les équations de champ d'Einstein. Ce dispositif apparaît si important dans la formulation finale de RG, que la plupart des physiciens réservent le terme "champ de gravitation" pour les champs produits par la matière. Les expressions "partie plate de l'Espace-temps", et partie de "Espace-temps sans champs de la gravitation" sont synonymes dans le langage moderne. La "RR" et "l' Espace-temps plat" sont ainsi également synonymes, ou presque, on peut chicaner pour savoir si l' Espace-temps plat avec une topologie non triviale (par exemple, Espace-temps cylindrique) est incluse dans la "RR". Par ailleurs, l'utilisation "moderne" est apparue assez tôt. Le livre d'Eddington la théorie mathématique de Relativité (1 922) définit la relativité Restreinte comme la théorie de Espace-temps plat.

L'utilisation moderne remet le champ "de la gravitation" uniforme de nouveau à son statut originel de pseudo-champ, avec toutes les connotations péjoratives du préfixe "pseudo". Et le critère véritable d'un problème de RG (c.-à-d., pas de RR ) est que le Espace-temps n'est pas plat. En revanche, le libre choix des diagrammes, la forme moderne du principe général de la relativité, est très ouvert. Vous pouvez employer des coordonnées curvilignes dans l'Espace-temps plat. (si vous employez des coordonnées polaires dans la géométrie plate, avez-vous soudainement quitté le royaume d'Euclide?)

La version habituelle du paradoxe de Langevin le qualifie comme un pur problème de RR, par référence aux normes modernes. L' Espace-temps est l'Espace-temps plat ordinaire de Minkowski. Le référentiel de Stella est juste un système de coordonnées curvilignes.

L'explication par le diagramme d'Espace temps est plus près de l'esprit de RG (crû 1916) que la prétendue explication de "RG". Espace-temps, géodésiques, et intervalle invariant, constituent le coeur de la RG.

Le Paradoxe de Langevin: L'Objection de la discontinuité temporelle

Faisons une supposition.

Supposons le demi tour instantané. La Relativité impose une limite supérieure aux vitesses, mais pas aux accélérations. Un demi tour instantané est un cas limite d'un demi tour court, donc la théorie devrait traiter ce cas.

Pendant le trajet aller, Terence vieillit de moins de 2 mois selon Stella ( 12 mois de Stella, Facteur de dilatation temporel = 7). Sur le trajet retour, Terence vieillit pareil, car les mêmes calculs de Stella s'appliquent aussi. Si le demi tour est instantané, il semblerait donc que Terence n'ait vieilli que de 4 mois à peine. Pourtant on prétend que Terence a vieilli de 14 ans quand Stella le recroise au retour ! Où sont donc passés les années manquantes ?

L'explication par l'effet Doppler répond à cet argument. Stella voit ( via son télescope) Terence vieillir très lentement sur le trajet aller , mais prendre pratiquement 14 ans sur son trajet retour. Pas de discontinuité temporelle !

Certes elle calcule quelque chose de différent en tenant compte de l'effet Doppler et de la vitesse finie de la lumière. Ces calculs sont valables pour des référentiels inertiels. En fait pour Stella, elle obtient 2 mois pour le référentiel correspondant au le trajet aller et 2 mois sur le référentiel correspondant au trajet retour ( cf ci-dessus) , et pour obtenir 4 mois elle doit additionner des quantités mesurées dans deux référentiels différents (elle a changé "instantanément" de référentiel inertiel à mi course).

Mais des référentiels inertiels différents ont des critères différents de simultanéité. Le référentiel "trajet aller" dit : "Au moment où Stella fait son demi tour, l'horloge de Terence marque environ 2 mois depuis le départ". Le référentiel du trajet retour dit : " Au moment où Stella fait son demi tour, l'horloge de Terence marque environ 13 ans et 10 mois. La prétendue discontinuité n'est autre qu'une erreur de décompte des temps, causée par le passage d'un référentiel à un autre [point important pour bien comprendre, la simultanéité en Relativité Restreinte pour des objets distants dans des référentiels différents, ne s’observe pas directement et n’a pas de caractère absolu ]

L'explication par le diagramme d'espace temps renvoie à la même solution.

Le Paradoxe de Langevin: L' Objection de dépendance de la distance.

Dans notre exemple standard ( voir introduction) le calcul du vieillissement de Terence par Stella est le suivant: 1/7 année pendant son trajet aller, 1/7 d'année pendant le trajet retour et le reste 14 ans moins 2/7 d'année pendant le demi tour.

Rappellons qu'elle fait son demi tour en un jour selon Terence, soit environ 15 heures de son temps propre à elle (nous vous faisons cadeau des minutes ..).

Si Stella fait, dans les mêmes conditions, un voyage plus long, prenant 2 ans au lieu d'un sur chacun des trajets aller et retour soit un total de 4 ans de son temps propre, il s'écoulera 28 ans selon Terence. Mais si elle effectue le même demi tour, il prendra le même temps ( 15 heures de son temps propre).

Alors quand Stella et Terence fêteront leurs retrouvailles fugaces, Terence aura vieilli de 28 ans ( plus un jour). Stella décompte le vieillissement de Terence comme suit: 2/7 d'années sur le trajet aller, 2/7 d'année sur le trajet retour, donc Terence s'est pris, cette fois ci, un coup de vieux de plus de 27 ans pendant le demi tour, soit environ deux fois plus que dans notre exemple standard, alors que Stella a opéré le demi tour dans le même temps, ce que Terence confirme.

La Solution est similaire à celle que nous avons donnée pour l'objection de discontinuité temporelle. La façon dont Terence vieillit, n'est pas quelque chose que l'on peut observer directement en RR. L'explication par l'effet Doppler s'appuie sur ce que Terence et Stella voient vraiment avec leurs télescopes, ce qui élude la difficulté. Le décompte de Stella est un décompte qui dépend du référentiel inertiel, et pendant tout le demi tour elle change de façon continue de référentiel inertiel. Pas étonnant qu'un décompte qui ignore ce point conduise à des résultats inattendus. Voir l'objection de discontinuité temporelle pour plus de détails.

Trop d'explications: une Méta-Objection

Vieille plaisanterie de prétoire:

"Votre Honneur, je vais d'abord montrer que mon client n'a jamais emprunté le vase Ming du plaignant, ensuite qu'il a rendu le vase en parfait état et enfin que la fêlure était déjà présente quand il l'a emprunté."

Pourquoi tant d'explications ? Les tenants de la Relativité chercheraient ils à noyer le poisson?

Pour valoir quelque chose le plaidoyer d'un avocat de la défense n'a besoin que de semer le doute vis à vis du bien fondé de la plainte.

Mais une théorie physique doit nous tenir un discours homogène et cohérent.

La théorie paie ici le prix de sa versatilité. Elle nous dit : Prenez le référentiel qui vous plait pour décrire vos résultats, ou utilisez un diagramme d'espace temps et ne choisissez aucun référentiel privilégié. Aucune importance: Cela n'est pas surprenant qu'une explication se décline en plusieurs versions.

La plupart des physiciens considèrent l'explication par le diagramme d'espace temps comme l'explication fondamentale. Sa nature géométrique fournit une trame Universelle qui sert de support aux autres explications apparemment différentes et montre quelles ne sont que différents aspects de la même.

La Figure 1 représente le diagramme d'espace temps de notre héro et de notre Héroïne. En complétant avec des lignes dans une directions ou l'autre nous allons retrouver les différentes explications. Nous avons choisi c = 1 , ainsi les rayons lumineux seront à 45 ° dans tous nos diagrammes

La figure 2 est le diagramme correspondant à l'explication par l'effet Doppler. Les lignes rouges à 45° sont les impulsions de lumière que chacun des jumeaux envoie à l'autre. Pour la clarté on a fait deux diagrammes correspondant aux deux sens, celui de gauche montre les impulsions émises par Stella, celui de droite celles émises par Terence.

Le facteur de dilatation temporel dans le diagramme est de deux. Terence vieillit deux fois plus que Stella. Notons que Stella n'a le temps que d'envoyer 16 impulsions alors que Terence peut en envoyer 32.

Les impulsions sont espacées régulièrement du point de vue de leur émetteur, mais les réceptions ne le sont pas du fait du décalage vers le rouge ou le bleu lié au mouvement relatif. Sur le diagramme on a essayé de représenter les impulsions aussi correctement que possible. Vérifier l'explication par l'effet Doppler pour les détails.

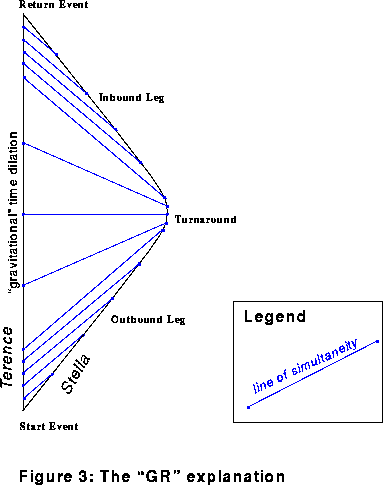
Figure 3,Le diagramme relatif à l'explication par la relativité générale, est complété par des lignes de simultanéité ( en bleu) au lieu d'impulsions lumineuses

Ces lignes représentent le lieu géométrique des événements qui se déroulent simultanément selon Stella .

On peut voir comment les lignes sont bien groupées sur la ligne d'Univers de Stella et dispersées sur la ligne d'Univers de Terence. Ceci est une représentation graphique de la dilatation gravitationnelle du temps.

En modifiant légèrement la figure 3 nous obtenons une description correspondante à l'objection de discontinuité temporelle ( figure 4).

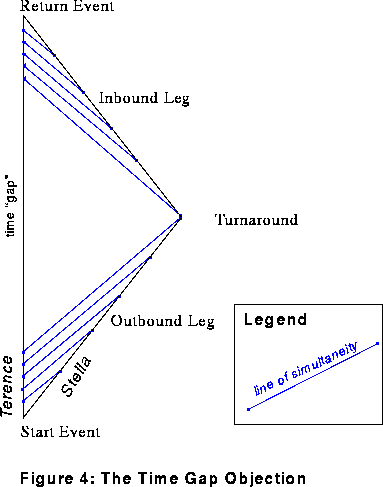
Ici nous avons supposé le demi tour instantané. Sur le trajet Aller Stella utilise un référentiel inertiel de référence et la même notion de simultanéité que précédemment alors que sur le trajet retour elle commute vers un autre référentiel

La discontinuité temporelle ( la partie de la ligne d'Univers de Terence dépourvue de lignes bleues) est une conséquence de cette commutation brutale.

Ce ne sont là que quelques méthodes pour décorer un diagramme simple avec des lignes. Dans l'esprit du "Laissez faire" de la Relativité, nous pourrions couvrir le diagramme avec n'importe quel réseau de grilles de lignes, et obtenir une description du système de coordonnées résultant. Je me dépêche d'ajouter que cela ménage toutefois quelques chausse-trappes pour les imprudents, voir Section 6.3 de Misner, Thorne, et Wheeler pour les détails

Moralité : Un seul territoire, beaucoup de cartes.