Table des matières

Pourquoi des tenseurs en RG ?

Changement de coordonnées locales

Notion de Tenseur : Construction de l’objet géométrique « tenseur »

Espace Vectoriel

Espace vectoriel dual

Notion de tenseur, exemples

Présentation physique : Utilisation des « tenseurs »

Scalaire : Tenseur d’ordre zéro

Vecteurs : Tenseurs d’ordre un

Tenseurs d’ordre deux, et plus

Tenseurs d’ordre deux et Matrices

Opérations sur les tenseurs

Le tenseur métrique, exemples

Dérivation de tenseurs, la dérivée covariante, la connexion métrique

Exemples de tenseurs importants en RG

L’équation tensorielle de la RG développée

Annexe : L’équation géodésique

Exercice : La dérivée covariante

Pourquoi des tenseurs en RG ?

Le «  principe*  de Relativité Générale » stipule que les lois de la physique peuvent être décrites dans n’importe quel référentiel (inertiel ou non inertiel).

Si on a écrit ces lois dans un référentiel, pour les transposer dans un autre référentiel, il faut opérer la transformation de «  coordonnées » correspondant au passage de l’ancien système de coordonnées vers le nouveau.

L’objectif recherché est de trouver une formulation des lois qui fasse que par n’importe quelle transformation de coordonnées (locale, car les lois de la RG s’expriment par des équations différentielles locales, en vertu du principe d’équivalence), la forme de lois soit conservée : Si une relation entre des paramètres existe dans un référentiel, la même relation entre les valeurs (différentes) de ces mêmes paramètres existe dans les autres. Il se trouve que les tenseurs possèdent précisément de cette propriété.

Autrement dit : Si j’arrive à écrire une loi en RG sous forme de relation entre tenseurs, si elle est vraie dans un système de coordonnées (un référentiel quelconque), alors elle est vraie dans tous ! On dit alors que ces équations sont «  généralement covariantes »

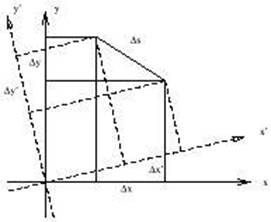
Changement de coordonnées locales dans un espace quelconque

Quelques rappels :

Le tenseur métrique détermine localement, un invariant ( ds²) :

Dans un espace plat, le tenseur métrique est indépendant du point l’espace

Dans un espace courbe, le tenseur métrique dépend du point. (On y reviendra ..)

Notion de tenseur : Construction de l’objet géométrique «  tenseur »

Espace vectoriel Eⁿ

C’est un ensemble d’objets (vecteurs) V, qui peuvent être comparés, additionnés (muni d’une structure de groupe) et multipliés par des nombres réels (corps) de façon linéaire. Soit V et W deux vecteurs de cet ensemble et a et b deux nombres réels:

(a+ b).( V + W) = a.V + b.V + a.W + b.W. (1)

Le nombre de vecteurs linéairement indépendants (n) définit la dimension de l’espace Vectoriel. Les vecteurs définis dans cet espace vectoriel sont dits «  contravariants »

Un jeu de n vecteurs linéairement indépendant définit une base ( ê₀, …ê_µ,…ê_n). On définit par V^µ les « composantes » d’un vecteur V, conformément à (1), par :

V =Σ_{µ =1 à n} (V^µ. ê_µ ) = V⁰. ê₀+V¹. ê₁+ …+Vⁿ. ê_n = V^µ. ê_µ (Convention d’Einstein) (2)

Pour simplifier la notation, on ne fait référence en général, qu’aux composantes des vecteurs (la base est sous entendue)

Nous sommes tellement habitués à l’isomorphisme entre notre espace physique et R³, qu’on en oublie combien cette idée d’associer à chaque point de l’espace des coordonnées et de transformer un problème de géométrie en un problème de calcul sur R³ a été une percée non triviale.

Soit un vecteur V de cet espace vectoriel ( qu’on appelle vecteur contravariant en abrégé ou vecteur tangent, ou tout simplement « vecteur ») de composantes contravariantes V^µ dans un système de coordonnées local C1( x^µ).

Evaluons les composantes V^µ ’ de ce même vecteur V, dans un autre système de coordonnées C2 (x’^µ ) au même point, alors la loi de transformation la plus générale (valable dans n’importe quel espace) est :

V^µ ’ = (∂ x’^µ /∂ x^µ) . V^µ (3)

Il suffit de remarquer que c’est le même vecteur qui est décrit dans les 2 bases, et évaluer les vecteurs ( ê_µ ) de la base d’origine dans la seconde (ê_µ’) et de substituer.

V = V^µ. ê_µ = V^µ’. ê_µ’ (4)

Avec ê_µ = (∂ x’^µ /∂ x^µ) ê_µ’ (5)

On les appelle « contravariants » du fait que la loi de transformation des composantes est l’inverse de la loi de transformation des vecteurs de base.
Espace vectoriel dual E_n

Sur l’espace vectoriel Eⁿ défini précédemment on peut définir une  forme linéaire F (vecteur dual ou vecteur à composantes covariantes, vecteur covariant en abrégé, ou vecteur cotangent), telle que si on a deux vecteurs ( contravariants) V,W et deux nombres réels a,b, on a :

F ( aV +bW) = aFV + bFW = R ( R est un nombre réel) (6)

Une forme linéaire appliquée sur un vecteur produit un nombre.

Comme V = V^µ. ê_µ -> F.V = V^µ .F ( ê_µ) (7)

On voit que F ( ê_µ) est la composante F_µ, correspondante à ê_µ, de la forme linéaire

En pratique, on peut s’arrêter là. Exemple : trouver la forme F qui aux vecteurs

(4,2,0), ( 1,2,-3), (0,2,5) de R³ associent respectivement les scalaires (2,-7,-1)

4.F (e₁) + 2 .F(e₂) = 2

1.F(e₁) + 2.F(e₂) – 3 F(e₃) = -7

2.F(e₂) + 5.F(e₃) = -1

On trouve: F(e₁) = 2, F(e₂) = -3, F(e₃) = 1

Pour être Formel, on va introduire des vecteurs de base de cet espace dual:

Définissons ω ^ν comme une base de cet espace dual par : ω^ν .ê_µ = δ_µ^ν

δ_µ^ν est le symbole de Kronecker qui vaut 1 si µ = ν et 0 autrement

F s’écrit alors F_ν ω^ν où (7) s’écrit F.V = V^µ F_ν .ω^ν .ê_µ = V^µ F_ν.δ_µ^ν (8)

Ces formes linéaires forment un ensemble muni d’une structure d’espace vectoriel de même dimension n noté « E_n » (satisfont aux axiomes d’espace vectoriel)

Sans refaire tous les calculs on montrerait ( exercice) que pour un vecteur « covariant » (noté maintenant V_µ pour homogénéiser la notation ), la loi de transformation est :

V_µ ’ = (∂ x^µ /∂ x’^µ) . V_µ

On a : V^µ . V_µ= Scalaire ( Invariant par transformation de coordonnées) (9) A noter que le dual du dual est l’espace d’origine.

Nous avons maintenant les briques de bases pour introduire les tenseurs

Notion de tenseur

Produit tensoriel : Soit deux espaces vectoriels Eⁿ à n dimensions et E^m à m dimensions

Soit un vecteur V = V^µ. ê_µ , appartenant à Eⁿ

Soit un vecteur W = W^ν. ê_{ν ,} appartenant à E^m

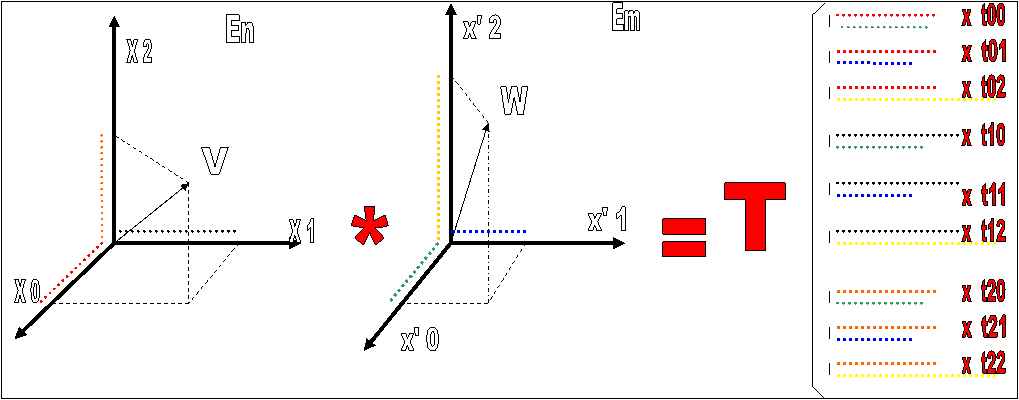
t00 = V⁰.W⁰, t01 = V⁰.W¹, …. T22 = V².W².

On définit le tenseur T tel que T = V *W ( l’opérateur « * » dénote le produit tensoriel) de la façon suivante :

Les composantes T^µν = V^µ * W^ν de ce tenseur sont tous les produits croisés des composantes des vecteurs ( n.m composantes)

La « base » de ce tenseur est le produit tensoriel des vecteurs de base ê_ν *ê_µ ( n.m)

T est un objet de l’espace Tensoriel Eⁿ * E^m , produit tensoriel des espaces vectoriels Eⁿ et E^m .

Loi de transformation : On voit que par construction le loi de transformation des tenseurs va être le produit de celles des vecteurs ( contravariants ou covariants)

T^µ’ν’ = (∂ x’^µ /∂ x^µ) (∂ x’^ν /∂ x^ν) T^µν (10)

Pour un tenseur deux fois contravariant
Exemple

Un tenseur deux fois contravariant (µ,ν) , à 4 dimensions pour chaque indice (µ et ν varient indépendamment de 0 à 3 : espace temps de la RG), est un objet mathématique à 16 composantes ( scalaires, ou fonctions s' il existe un espace vectoriel en chaque point de l'espace temps) qui peut être visualisé par exemple sous forme d'un tableau 4x4 

êT⁰⁰ T⁰¹ T⁰² T⁰³ ê

êT¹⁰ T¹¹ T¹² T¹³ ê

T^µν = êT²⁰ T²¹ T²² T²³ ê = V^µ * W^ν

êT³⁰ T³¹ T³² T³³ ê

V⁰ * W⁰ = T⁰⁰ , V⁰ * W¹ = T⁰¹ , …., V³ * W³ = T³³

Cette construction peut évidemment être généralisée à un nombre quelconque de produits tensoriels d’espaces vectoriels et d’espaces vectoriels duals. On va définir un tenseur p fois contravariant et q fois covariant par sa variance ( p,q) et la dimension (n) de l’espace vectoriel de chacun des indices. En RG cette dimension est quatre pour tous les indices.

Exemple : tenseur 2 fois covariant ( antisymétrique de surcroît)de l’électromagnétisme

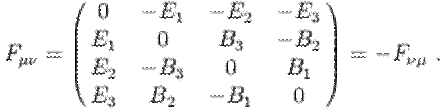
Chaque composante F_µν = ∂_νA_µ- ∂_µA_ν dérive d’un quadri-vecteur potentiel A_µ.

Avec ce tenseur, les lois de Maxwell s’expriment très simplement. L’invariance de jauge par la substitution A_µ -> A_µ + ∂_µ F   saute aux yeux .

A noter, que dans notre première approche «  mathématique », nous avons «  construit  l’objet géométrique » tenseur, qui jouit par construction de certaines propriétés, nous allons en physique, souvent oublier cette construction pour ne nous intéresser qu’aux propriétés de transformations vis à vis des transformations de coordonnées.

Scalaires ( Les scalaires sont des tenseurs !)

Ce sera notre premier tenseur, le plus simple, mais pas le moins important, il est de variance (0,0)

En établissant l’expression de l’intervalle ds², dans un référentiel arbitraire {X_i}, on a implicitement postulé l’invariance de la valeur numérique du ds², lors d’un changement de référentiel ( x’_µ au lieu de x_µ).

L’intervalle ds² est un scalaire, c.a.d la donnée en chaque point de l’espace temps d’un nombre indépendant du choix d’un référentiel particulier.

De façon générale on appelle scalaire tout champ S(x) tel que dans un changement arbitraire de référentiel produisant S’ (x’) on ait : S(x) = S’ (x’).

On peut facilement construire d’après (9) des scalaires ( invariants ) en « combinant* » par exemple un vecteur** contravariant et un vecteur** covariant.

· * En fait c’est le produit scalaire «  généralisé » en Relativité.

· ** Les vecteurs sont des tenseurs comme on va le voir.

Les Vecteurs ( les vecteurs sont des tenseurs)

Quadrivecteur contravariant : tenseur de variance (1,0)

On suppose maintenant connu la notion de vecteur défini dans un espace vectoriel, ensemble dont les éléments sont les vecteurs muni d'une relation d'égalité, d'une loi interne d'addition commutative, associative munie d'un élément neutre et d'un inverse et d'une loi externe de multiplication par R, corps de réels (distributive,...).

Le qualificatif contravariant vient de ce que, lors d'un changement de base les coordonnées (x^µ) varient selon la transformation inverse de celle des vecteurs de la base (ê_µ).

En physique ( en RR en particulier), un champ de (quadri)vecteurs a un caractère intrinsèque qui peut être défini indépendamment du référentiel :

Exemples 

Vecteur quadri vitesse U^µ = dx^µ/dt avec dt invariant car : dt = ds²/c².

Vecteur quadri énergie-impulsion ( remplace l’énergie en RR) qui par «  produit scalaire » va produire le scalaire  « m.c² » ( invariant en RR) indiquant l’invariance de la masse relativiste ( contrairement aux idées reçues, la masse est un invariant en RR)

Autre définition d’un tenseur contravariant ( défini par ses propriétés vis à vis des transformations): Tout objet défini par rapport au système de coordonnées ( base d’un espace vectoriel de dimension 4 dans ce cas) par 4 grandeurs A^µ et qui se transforme selon la loi: A'^µ= (¶x'^µ/¶x^ν).A^ν (11)

est aussi appelé quadrivecteur ( tenseur de variance 1,0) contravariant

Quadrivecteur covariant

Un ensemble de 4 grandeurs A_µ est appelé quadrivecteur covariant si pour n'importe quel choix de vecteurs contravariants B^µ on a :

A_µB^µ= invariant ( par changement de coordonnées), c.a.d produit un scalaire.

On en déduit la relation: A'_µ= (¶X^ν/¶X'^µ).A_ν

Rappelons la dualité entre l’espace vectoriel des vecteurs contravariants et covariants (si l’un est un espace vectoriel de référence, l’autre est l’espace vectoriel, dual, des formes linéaires sur ce premier et vice versa, le dual du dual est l’original).

Tenseur contravariant ( enfonçons le clou !)

Exemple tenseur de rang 2 : Notion de tenseur ( produit tensoriel).

On forme les 16 produits A^µν des composantes A^µ et B^ν de 2 quadrivecteurs contravariants:

A^µν= A^µ * B^ν

On appelle cette opération "produit tensoriel", les 16 composantes ainsi produites sont les composantes du tenseur A^µν , à noter que le tenseur résultant a ses composantes µ dans l'espace vectoriel associé au vecteur A^µ et ses composantes ν dans l'espace vectoriel associé au vecteur B^ν

Des propriétés des vecteurs on déduit: A^µν=(¶x^µ/¶x^λ)(¶x^ν/¶x^ρ).A^λρ

Par extension, on appelle tenseur contravariant de rang 2 tout objet de composantes A^µν qui satisfait la relation ci dessus

Cette propriété caractérise un tenseur contravariant

Tenseur covariant

De même, on appelle tenseur covariant d'ordre 2 un objet de composantes A_µν qui satisfait la relation

A_ρλ=(¶x_µ/¶x'_ρ)(¶x_ν/¶x'_λ)A_µν

Cette propriété caractérise un tenseur covariant

Un tenseur covariant d'ordre 2 prend un tenseur contravariant d'ordre 2 ( ou 2 vecteurs contravariants) en entrée et produit un scalaire en sortie. Cela se généralise aux ordres supérieurs

Le produit d’un tenseur contravariant ( ou de n vecteurs contravariants) par un tenseur covariant de même rang et dimension produit un scalaire , c’est à dire quelque chose d’invariant par rapport aux coordonnées.

Tenseur mixte et de rang supérieur à 2

C'est le tenseur de plus général qui possède des composantes contravariantes et covariantes dont les tenseurs présentés précédemment ne sont de des cas particuliers.

La loi à laquelle il obéit est évidente (extension et combinaison des lois précédentes)

Une autre présentation rigoureusement équivalente et plus "intuitive" est la suivante

Un tenseur T^j,_k , noté de variance (j,k), j fois contravariant et k fois covariant prend en entrée j vecteurs covariants et k vecteurs contravariants et génère un nombre.

Ce nombre en sortie est une fonction linéaire des entrées.

Une autre manière est de dire qu'il prend en entrée k vecteurs contravariants et produit en sortie j vecteurs contravariants, ce qui est équivalent car si on rajoute en entrée les j vecteurs covariants ils "mangent "les j vecteurs contravariants pour produire un nombre!!

Tenseur d’ordre deux (dimension n) et matrice (n x n)

Bien qu’il s’agisse d’objet mathématiques de natures différentes, un tenseur de variance ( 1,1) a les mêmes règles opératoires qu’une matrice n x n.
Quelques opérations utiles sur les tenseurs

On peut additionner ( soustraire) des combinaisons linéaires de deux tenseurs de même variance de même dimension d’indice. On obtient un tenseur de même variance, dont chaque composante est la somme ( soustraction) des composantes correspondantes.

On peut multiplier des tenseurs  par un scalaire.Chaque composante est multipliée par le scalaire)

Multiplier de façon externe deux tenseurs: T _µνλ = A_µν.B_λ par exemple ( on multiplie deux à deux toutes les composantes du premier par toutes celles du second)

La variance est la somme des variances.

Contracter les tenseurs ( sommer indice haut sur indice bas ) Contraction de R_µ^ρ_νλ

On fait λ=ρ et on somme R_µ^ρ_νρ R_µν

Elever /abaisser les indices à l’aide respectivement du tenseur métrique inverse ou du tenseur métrique.

R_µ^ρ_νλ. g_ρσ = R_µσνλ , à noter que les composantes du tenseur métrique inverse sont les cofacteurs/déterminant de celles du déterminant du tenseur métrique d’où g^µν.g_µν = 4

Le tenseur métrique ( la vedette)

Ce qui précède nous amène à introduire ce tenseur fondamental g_µν de variance (0,2) et son inverse g^µν de variance (2,0) qui satisfont à :

C’est en particulier le variable dynamique utilisée dans les équations de la RG

L'importance du tenseur métrique dans les espaces courbés est telle qu'un nouveau symbole g_mn lui a été attribué (h_mnest réservé à la métrique de Minkowski). Ce tenseur est général, sa seule contrainte étant qu'il doit être un tenseur (0,2) symétrique. Sauf cas particulier, il est non dégénéré, ce qui veut dire que son déterminant g = | g_mn| n'est pas nul.

La symétrie de g_mn implique que son inverse g^mn l'est aussi. Comme en relativité restreinte , la métrique et son inverse peuvent être utilisés pour abaisser ou élever des index.

La métrique joue un rôle central et déterminant dans la théorie de la Relativité , citons quelques unes des propriétés et applications de g_mn :

(1) La métrique fournit une notion de passé et de futur.

(2) La métrique permet le calcul de la longueur des chemins et du temps propre.

(3) La métrique détermine le chemin le plus court entre deux points, et par la même, la trajectoire des particules.

(4) La métrique remplace le champ gravitationnel Newtonien F.

(5) La métrique fournit la notion de référentiel localement inertiel, en conséquence un critère d'absence de rotation.

(6) La métrique détermine la causalité, en définissant les chemins suivis par la lumières comme les plus courts possibles, plus courts qu'aucun autre chemin suivi par un quelconque autre signal ou des particules réelles.

(7) La métrique va permette de réaliser les opérations qui remplacent le produit scalaire de l'espace Euclidien traditionnel de la mécanique Newtonienne, etc..

Ces propositions ne sont pas indépendantes, mais illustrent l'importance de ce tenseur.

Exemples de tenseurs métriques d’espace temps n = 4 (sous forme diagonale)

Minkowski (dt,dx,dy,dz) -1 1 1 1

Schwarzschild (dt,dr,dθ,dφ) -(1-2GM/r) (1-2GM/r)^-1 r² r²sin²θ

Robertson Walker (dt,dr,dθ,dφ) -1 a²/1-kr² a².r² a²r²sin²θ

Dérivée covariante d'un vecteur, connexion métrique

Si on calcule la dérivée d’un vecteur par les lois habituelles de dérivation, l’objet qu’on obtient, pourrait à première vue ressembler à un tenseur à deux indices. Par contre, comme il n’obéit pas à la loi de transformation des tenseurs, ce n’est pas un tenseur. Nous sommes amenés à définir une nouvelle dérivée, la dérivée covariante, obtenue à partir de la dérivée classique, par « ajout » d’un terme correctif qui se combine linéairement avec le vecteur pour que le résultat soit un tenseur.

En RG, Г _μ^ν_λ, est le « symbole de Christoffel », qui n’est pas un tenseur, qui caractérise la «  connexion métrique » de l’espace temps courbe, et s’exprime complètement en fonction de la métrique et de ses dérivées.

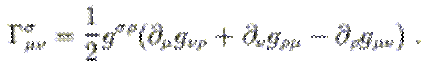
Il existe aussi des connexions non métriques, qui ne sont pas utilisées en RG.

Vous trouverez un exposé formel d’introduction de la dérivée covariante et de la connexion en : http://www-cosmosaf.iap.fr/MIT-RG3F.htm

Dérivée covariante d'un tenseur

La dérivée classique d’un tenseur n’étant pas un tenseur, pour conserver ce caractère tensoriel il faut apporter une succession de termes correctifs (un par élément de variance) et définir par là une dérivée covariante.

La forme générale de la dérivée d’un tenseur de variance (k,l) est :

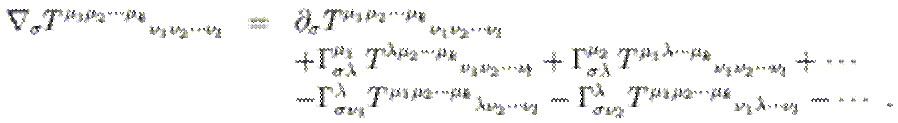
En fait pour un vecteur ( tenseur(0,1)) la dérivée covariante corrige la variation intrinsèque propre à la courbure de la courbe sur laquelle on opère la dérivation, et rend ainsi compte uniquement de la variation relative du tenseur par rapport a la courbe.

Transport parallèle d'un vecteur

Le transport // d'un vecteur le long d’une courbe s'obtient en déplaçant le vecteur de façon à conserver l'angle qu'il fait localement avec la courbe (tangente à la courbe).

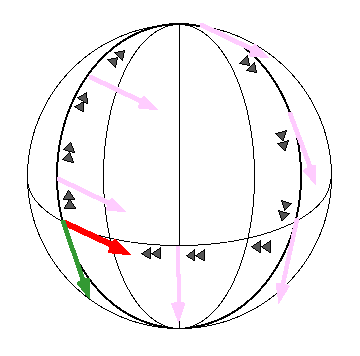
On voit que le résultat dépend du chemin suivi, ce qui explique la difficulté conceptuelle de comparaison des objets dans un espace courbe.

Tenseurs particulièrement utilisés en Relativité Générale

Tenseur de Riemann

Einstein a cherché comment construire un tenseur ne contenant que les dérivées premières et secondes des éléments du tenseur métrique pour construire dans le domaine tensoriel covariant l'équivalent de l'équation de Poisson. Il est tombé sur le tenseur de Riemann (solution unique ).

Ce tenseur s'établit indépendamment, de façon théorique en faisant parcourir dans un système de coordonnées curvilignes un parallélogramme infinitésimal et en comparant les orientations de départ et d'arrivée d'un vecteur transporté parallèlement sur la courbe.

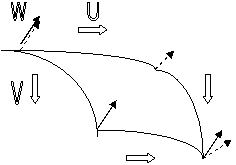
La différence traduit la courbure et s'exprime par un tenseur assez compliqué: le tenseur de Riemann mixte du 4éme ordre ( 3 fois covariant et une fois contravariant ) dont les éléments sont les dérivées premières et secondes des éléments de la métrique.

A noter que cette courbure est une quantité du deuxième ordre.

ddê_i - ddê_i = ê_j.R_i^j_kl.dy^k.dy^l

L'espace est supposé sans torsion ( le parallélogramme curviligne est fermé ).

Ce tenseur fondamental décrit complètement la Courbure intrinsèque de l'espace temps au point considéré, mesurable par des observateurs confinés dans cet l'espace. ( généralisation à N dimensions de la Courbure de Gauss ). Ne pas confondre avec la courbure extrinsèque que pourrait avoir l'espace, s'il était plongé dans un espace de dimensions supérieures et qui serait mesuré par des observateurs vivant dans cet espace.

R_jⁱ_kl = ¶Gⁱ_jl/¶x_k - ¶Gⁱ_jk/¶x_l +Gⁱ_mk.G^m_jl - Gⁱ_ml.G^m_jk

Quelque chose de compliqué à calculer, combinaison de différences de dérivées de Symboles de Christoffel et de différence de produits de ces symboles.

Ce tenseur possède de nombreuses symétries ( 20 composantes différentes pour 256 possibilités) et décrit exhaustivement la courbure locale de l'espace.

Si par un choix de coordonnées , les éléments du tenseur métrique sont localement constants à un point P, (référentiel chute libre correspondant à un espace tangent de Minkowski), alors le tenseur de Riemann est localement nul au point P ( la dérivée première du tenseur métrique=0)

Et s'il est nul dans un référentiel donné, il l'est dans tous, propriété fondamentale de la RG

En revenant à la définition intuitive des tenseurs, le tenseur mixte de Riemann, 3 fois covariant et 1 fois contravariant , va prendre en entrée 3 vecteurs contravariants U,V,W et produire en sortie un vecteur contravariant W' qui est issu du transport de W le long du parallélogramme curviligne infinitésimal défini par U,V ,

R(u,v,w)^j = R_i^j_kl.Uⁱ,V^k,W^l

Le tenseur de Riemann possède de nombreuses (anti)symétries. En utilisant la forme complètement covariante R_mnrs = g_drR_m^d_ns on a :

R_mnrs = R_rsmn, R_mnrs = - R_nmrs = - R_mnsr = R_nmsr, R_mnrs + R_msnr + R_mrsn = 0

Ce n’est pas tout : le tenseur de Riemann étant le commutateur de 2 dérivées covariantes, sa dérivée covariante D_i est nulle.

Plus exactement on obtient l’identité de Bianchi  :

D_d R_mnrs + D_s R_mndr + D_r R_mnsd = 0

Celle-ci joue un rôle essentiel dans la théorie de la relativité générale. Par contraction, elle devient :

D_m [ R_mn - g_mn R ] = 0

Ou on trouve les tenseurs et scalaire de RICCI

Cette forme suggère directement le tenseur d’Einstein ( Seul tenseur construit à partir des dérivées premières et seconde du tenseur métrique et à divergence nulle)

Tenseur de Ricci :

Par contraction de deux indices on obtient le tenseur covariant d'ordre 2 de Ricci: Rij ( 10 composantes qui permettent de reconstituer 10 composantes du tenseur de Riemann).Ce tenseur rend compte au deuxième ordre de la variation de volume dans son parcours sur les géodésiques.

Mais où sont passées les 10 autres composantes ?

Bonne question: D'abord on ne peut pas annuler complètement le tenseur de Riemann, ce qui voudrait dire que par un changement de référentiel on compenserait un champ de gravitation (on ne le fait que très localement).

Par ailleurs le tenseur Impulsion Energie ne contient pas toutes les informations au sujet de la courbure , le tenseur de Weyl = W^a_bcd contenant le complément lié à la courbure propre de l'espace.

R_ij= ¶G_i^k_j/¶x_k- G_i^k_lG_j^l_k

Le tenseur de Ricci contrôle la dérivée seconde du changement de volume, d'un petit volume lors de sa trajectoire géodésique.

d²V/dx^a,dx^b= R_a,b .V^a.V^b

Le tenseur de Weyl contrôle la déformation ( sphère/ellipsoïde)

C'est le tenseur de Ricci qui figure dans l'équation, car la distribution de matière /énergie ne définit pas complètement le tenseur de Riemann.

Scalaire de Ricci

On l'appelle scalaire de courbure

Par multiplication du tenseur de Ricci par G^ij on obtient le scalaire de Ricci : R

Ce scalaire qui résulte de contractions multiples du tenseur de Riemann en synthétise les informations essentielles et est à ce titre très important ( cf principe de moindre action)

L’équation de la Relativité générale (équation d’Einstein) en Cosmologie

Rappel : R_mn-1/2(G_mn(R-2L)= - 8pGT_mn

Le tenseur de Ricci et le scalaire de Ricci présents dans le membre de gauche sont complètement déterminés par le tenseur métrique et ses dérivées premières et secondes ( via une combinaison des symboles de Christoffel décrivant les connexions métriques, que l'on peut calculer à partir de la métrique de RW.

êR₀₀ 0 0 0 ê | 1 | êT₀₀ 0 0 0 ê

ê R₁₁ 0 0 ê+ ½(R-2L) . | -a²/(1-kr²) | = - 8pG. ê0 T₁₁ 0 0 ê

ê R₂₂ 0 ê | -a²r² | ê0 0 T₂₂ 0 ê

ê R₃₃ ê | -a²r²sin²q | ê0 0 0 T₃₃ ê

R_µν = Tenseur de Ricci g_µν=Tenseur Métrique T_µν= Tenseur Impulsion/E

Tenseur de Rici: R_ij= ¶G_i^k_j/¶x_k- G_i^k_lG_j^l_k  , scalaire de Ricci: R=G^ij. R_ij T^ij=(p+r)Uⁱ.U^j - p.G^ij

et G_i^k_j = 1/2(G^lk )( ¶G_jl/¶x_i + ¶G_il/¶x_j - ¶G_ij/¶x_l )

On obtient alors les deux (compte tenu de l'isotropie spatiale en x,y,z) équations ci dessous

(2/a)(d²a/dt²)+(1/a²)(da/dt)²+Kc²/a² -L.c²= -8pGp/c² (1)

(3/a²)(da/dt)²+3Kc²/a² - Lc²= 8pGr (2)

Annexe : Equation Géodésique

Méthode 1 ( Géométrique la plus simple)

Partant du fait que la géodésique est une droite en RR on effectue le changement de coordonnées pour trouver son équivalent dans un système quelconque. Le résultat ne met pas directement en évidence que cette équation ne dépend que de la métrique.

Méthode 2 ( Définie par le vecteur tangent)

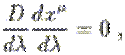qui implique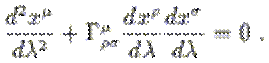

Méthode 3 ( Méthode «  physique » originale d’Einstein)

On écrit que la géodésique est la courbe qui minimise l'intégrale du chemin (ds).

En fait Einstein utilise sans le dire, le Lagrangien : L(x,dx/dp) = ½(g_µν). (dx^µ/dp) (dx^ν/dp) qui est L= ½(ds²/dp²) qui correspond à l’intervalle d’espace temps,

En appliquant les équations qui expriment la condition d’extremum: d/dp(¶L/¶(dx^µ/dp)) = ¶L/¶x^µ, On arrive à: d²x^s/ds²+ G_m^s_n .(dx^m/ds)(dxⁿ/ds) = 0

Rappelons que l'équation du mouvement géodésique) est contenue dans l'équation du champ.

Exercice : La dérivée covariante

Quels définitions et calculs pour vous mettre le pied à l’étrier

Dérivée covariante

Nous voudrions définir un opérateur de dérivée covariante qui réaliserait l'opération de dérivée partielle, mais de façon indépendante des coordonnées.

Propriétés fondamentales

Nous exigerons donc de qu'il soit une application linéaire de tenseurs (k, l ) vers des tenseurs (k, l + 1) avec les deux propriétés suivantes:

1. linéarité: <!-- MATH

$\nabla(T+S) = \nabla T + \nabla S$

-->(T + S) = T + S ;

2. règle de Leibniz (produit) : (T ÄS) = (T) ÄS + T Ä (S) .

Si obéit à la règle de Leibniz il peut toujours être écrit comme une dérivée partielle plus une transformation linéaire. Pour prendre la dérivée covariante, nous commençons par prendre la dérivée partielle et nous appliquons une correction pour rendre le résultat covariant ( nous n'allons pas en faire la preuve, mais vous la trouverez dans "Wald" si cela vous intéresse). Considérons le cas d'un vecteur Vⁿ. Cela signifie que pour chaque direction m, la dérivée covariante Ñ_m va consister en la dérivée partielle ¶_m plus une correction spécifiée par une matrice (G_m)^r_s. (une matrice n × n , où n est la dimension de la Variété pour chaque index m).

Coefficients de connexion

En fait les parenthèses sont généralement omises et nous écrirons ces matrices appelées coefficients de connexion, de la manière suivante G^r_ms. Nous avons donc

<TBODY>

(3.1) </TBODY>

Remarquons que dans le second membre, l'index original du vecteur V a été transféré vers , et le nouvel index ne sert qu'à la sommation. Si c'est bien l'expression de la dérivée covariante d'un vecteur en termes de dérivée partielle, nous devrions être capables de déterminer les propriétés de transformation de Gⁿ_ml, en exigeant que le membre de gauche soit un tenseur (1,1).

Propriétés des transformations des dérivées covariantes de Vecteurs

Donc, nous voulons que la loi de transformation soit :

<TBODY>

(3.2) </TBODY>

Commençons par le membre de gauche, on peut le développer en utilisant (3.1) et ensuite transformer les parties par les règles que nous connaissons :

<TBODY>

(3.3) </TBODY>

Le membre de droite peut être développé de façon similaire :

<TBODY>

(3.4) </TBODY>

Ces deux expressions doivent être égalées, le premier terme de chaque est identique et s'annule donc, alors nous avons :

<TBODY>

(3.5) </TBODY>

Où nous avons renommé l'index de sommation en . Cette équation doit être vraie pour tout vecteur V ^l, donc nous pouvons l'éliminer des deux membres. Ensuite les coefficients de connexion dans les coordonnées "primées" peuvent être isolées en multipliant par x^l/x^l'.

Le résultat est :

<TBODY>

(3.6) </TBODY>

Ce n'est évidemment pas une loi de transformation de tenseur, à cause du second terme.

Ceci est normal puisque les coefficients de connexion ne sont pas des tenseurs. Par construction, les 's sont non tensoriels puisqu'ils sont destinés à "corriger" et rendre tensoriels les dérivées partielles qui ne le sont pas, autrement dit annuler le terme qui détruit le caractère tensoriel (donc qui n'est pas un tenseur!) de l'expression (3,1). C'est pourquoi il faut être attentif aux placements des index dans les coefficients de connexion, ils ne sont pas des tenseurs et nous ne pouvons pas les abaisser ou les élever à l'envi.

Exercice : ( Difficile) Montrer que la dérivée partielle ¶_m d’un vecteur V ^l, n’est pas un tenseur :

Méthode suggérée : Appliquer les dérivées partielles dans chacun des systèmes de coordonnées, utiliser la loi de transformation des vecteurs V^µ ’ = (∂ x’^µ /∂ x^µ) . V^{µ ,} appliquer la loi de composition des dérivations partielles d’un système de coordonnées vers l’autre et remarquer que le résultat n’est pas conforme à la loi de transformation relative aux tenseurs. Attention aux manipulations d’indices !