La géométrie du disque en rotation en Relativité :

Avertissement : Un disque matériel en rotation rigide est un objet fictif. Nous nous intéressons ici aux effets relativistes et non pas à la déformation du disque matériel qui dépendrait de sa constitution (le matériau dont il est fait) et qui devrait faire intervenir la résistance des matériaux. Le disque sera supposé infiniment mince (sans masse) , en fait le problème formel est celui d’un référentiel en rotation uniforme. Mais comme c’est un peu abstrait, on parle de disque en rotation pour mieux illustrer le problème traité.

Résumé : L’étude du cas d’un disque rigide en rotation à des vitesses relativistes, traitée dans le cadre de cette théorie, soulève d’intéressants paradoxes, et fait l’objet de nombreux contresens d’interprétation, y compris par Einstein, Ehrenfest et quelques autres grands esprits du même acabit.

Qu’est ce qui a pu égarer des esprits aussi avisés, et en quoi sommes nous en mesure de donner aujourd’hui une démonstration et une interprétation que nous considérons comme définitive ( dans le cadre de cette théorie), là, où les concepteurs ont échoué?

Rappelons, qu’Einstein à cette époque, se concentrait sur l’élaboration de la théorie de la Relativité générale, qui lui donnait bien du fil à retordre. Un sujet comme le disque en rotation relativiste, qui faisait figure d’aimable casse tête intellectuel, physiquement irréaliste, n’a pas du le distraire beaucoup de ses préoccupations du moment. Les solutions classiques décrivent correctement les solutions réalisables (effet Sagnac ), ceci explique qu’il ait retenu de ce cas, que ce qui l’intéressait pour sa nouvelle théorie, sans aller au delà de sa vision intuitive du problème .

Revenons au points essentiels : L’application de la Relativité Restreinte dans le cas d’un disque, ne peut se faire qu’au niveau local, car la Relativité Restreinte s’appliquant à des référentiels inertiels, ils ne peuvent être que locaux, puisque, où que l’on soit sur le disque, il n’existe pas de référentiel global inertiel. Pire tous les référentiels locaux inertiels, définis en des points différents du disque inertiels sont différents, (une double infinité de référentiels).

On voit que l’on va jongler sans cesse entre les différents référentiels inertiels, gymnastique périlleuse, entre lesquels la simultanéité des évènements n’est pas assurée. (Comme le paradoxe de Langevin, qui est de même nature, nous l’a appris, en Relativité, la simultanéité n’a pas de caractère absolu).

Comme dans le paradoxe de Langevin, nous allons avoir des boucles spatio-temporelles, qui vont mettre en évidence des «  désynchronisations spatio-temporelles » (holonomies).

Deux observateurs ensembles, au départ, puis se séparant et suivant chacun des lignes d’univers dans des référentiels différents dont un au moins n’est pas inertiel (pour que la boucle puisse de fermer), vont se réunir à nouveau, plus tard, et vont constater des désynchronisations temporelles (l’un a plus vieilli que l’autre).

Appréhender la géométrie du disque en rotation telle que vue par les différents observateurs, est un vrai cauchemar, cette géométrie n’est pas définie, elle dépend de l’observateur !

Notre esprit est implicitement égaré, par le sujet traité. Le concept même de disque, implique, que dans notre esprit, la géométrie globale de l’objet est omniprésente ( c’est elle qui définit l’objet dont on parle), alors qu’on va voir que la perception de la géométrie qu’en ont les différents observateurs peut être très différente de celle d’un disque et qu’en particulier la périphérie mobile du disque et son environnement immédiatement externe ( fixe) ont des géométries différentes et ne coïncident pas géométriquement parlant, comme notre intuition, nous le laisserait supposer, mais que d’autres paradoxes de la relativité illustrent bien (rappelons nous comment un train en mouvement relativiste plus long qu’un tunnel, peut sembler y être contenu). Ici c’est poussé au paroxysme, car même sur le disque, un observateur va en avoir une vision déformée, du fait qu’en aucun point le référentiel inertiel local est identique à celui défini en un autre point . De nouveaux paradoxes apparaissent car alors que la géométrie spatiale du disque évaluée dans le référentiel en rotation attaché au centre du disque présente une courbure «  négative » c’est à dire que la circonférence est supérieure au rayon multiplié par 2pi, pour un observateur sur le disque, mais à la périphérie, s’il calcule le périmètre (vu par lui comme un cercle déformé) comme la Relativité le prescrit c’est l’inverse !

Pour bien comprendre ce qui suit, il faut donc oublier la géométrie globale, en jeu, traiter le problème localement dans les référentiels inertiels locaux et ne se ressouvenir de la géométrie globale qu’en tant que domaine d’intégration des équations locales.

Pour ceux qui veulent en savoir plus, suivez ces conseils et armez vous de courage et d’abnégation.

1-Présentation générale

1-1 Introduction

Je me suis pas mal inspiré du document «  The curvature of the Relativistic Rotating Disk » de Brian Keating ( sous la supervision du Dr Teymour Darkhosh. référence :

http://www.smcm.edu/nsm/physics/SMP03S/KeatingB.doc.pdf, dont j’ai fait une traduction, commentée disponible en :

http://www-cosmosaf.iap.fr/Disque%20en%20rotation.htm

Comme, j’ai relevé pas mal d’erreurs, de calculs et aussi parfois d’interprétation, sans que cela remette en cause l’approche épistémologique globale, ce document est difficilement lisible. La version qui suit est «  la mise au propre » du document commenté. Les quelques erreurs que je n’ai pas pu corriger pour des raisons pratiques étant mentionnées.

1-2 Simultanéité en Relativité ( Illustration et rappel)

Pour mettre en évidence ce point simplement, considérons seulement 4 référentiels inertiels (instantanés), K1, K2,K3 et K4, parmi l’infinité de référentiels différents possibles.

Voir figure 1

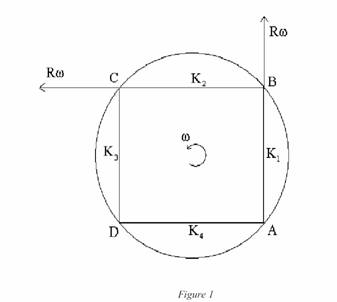
Les lettres A, B, C, D représentent des évènements (disons l’émission d’un éclair) qui se produisent à la périphérie du disque.

Je peux contraindre les évènements, A et B pour qu’ils soient simultanés dans K1, B et C simultanés dans K2, C et D simultanés dans K3, je dispose des degrés de liberté pour cela. Par contre, ayant utilisé tous mes degrés de liberté, je ne sais rien, et ne peux pas contraindre, la chronologie de D et A dans K4.

Si A et B sont simultanés dans K1, alors dans K2, lorsqu’on fait la transformation de référentiel K2/K1 on s’aperçoit que A est antérieur à B du fait du mouvement relatif de K1 par rapport à K2 de A vers B

{Quelques mots pour illustrer sans calcul, l’affirmation : La simultanéité s’apprécie dans K1 par le fait qu’un observateur O situé au milieu de AB, va voir les deux éclairs en même temps.

La lumière émise de A, va dans le même sens que le mouvement relatif de K1 par rapport à K2 dans cette direction, cette lumière émise de A, va donc à la rencontre des observateurs de K2, c’est pour cela que A va être vu avant B par les observateurs de K2.Les sceptiques pourront faire le calcul par les formules de Lorentz qui confirment ce point}

De même dans K3, B va être antérieur à C et dans K4, C va être antérieur à D.

Le problème présentant un caractère cyclique, en fermant le cycle, on est tenté de se demander si sur le dernier tronçon, K4, on a la même propriété : D et A sont simultanés dans K4,

Si je suppose que c’est le cas, on voit que D est antérieur à A dans K1. Si on suppose que ces relations d’ordre temporel sont «  transitives », on déduit par récurrence, que A est antérieur à B, qui est antérieur à C, qui est antérieur à D qui est antérieur à A ! . On arrive à une « contradiction », A est antérieur à A dans le référentiel K1. Hors du cas trivial, ou le disque est au repos, on voit que c’est absurde. Le fait simple de fermer la boucle nous suggère qu’une «  discontinuité » doit se manifester à cette occasion.

On voit sur ce exemple, qu’en relativité la notion de simultanéité, définissant « l’avant » et « l’après », est relative, dépend des référentiels considérés, et que la transitivité des relations n’est évidemment pas respectée dans le cas général.

1-3 Géométrie du disque en rotation

Un paradoxe plus fondamental et plus troublant a été proposé par Selleri dans l’article cité en référence [4].

Par un raisonnement élémentaire, on peut montrer, en supposant seulement que la circonférence du disque a une géométrie bien définie, que le rapport de la vitesse apparente de lumière en contre- rotation et co-rotation est donné par

où est la vitesse angulaire supposée constante, et R le rayon du disque, avec

,

et c+ et c- sont les vitesses de la lumière en co-rotation et contre rotation respectivement.

Le paradoxe se produit quand : et dans l’équation, (1.1), en gardant la vitesse tangentielle constante, soit :

Remarquons que l’accélération centrifuge :,.

Le référentiel associé au bord du disque tend donc vers un référentiel inertiel, se déplaçant à la vitesse : , par rapport à un observateur au centre, attaché au référentiel fixe.

Ceci crée une discontinuité, car on sait que dans un référentiel inertiel la vitesse de la lumière est la même dans les deux sens, soit :, résultat qu’on devrait trouver logiquement au passage à la limite dans ce cas.

Il n’en n’est rien, la formule (1.1), au passage à la limite indiquée, reste invariante, du fait de l’invariance de « v », et donne une valeur très différente.

On voit bien, que manifestement, une des hypothèses faites ne doit pas être valide.

1-4 L’Effet Sagnac

Il y a des confirmations de l’apparente « anisotropie » de la vitesse de la lumière sur un disque en rotation. Si un faisceau laser (cohérent) est fractionné en deux faisceaux (cohérents) se déplaçant en sens contraire sur le disque sur la périphérie d’un disque en rotation rapide (au moyen de miroirs semi transparents par exemple) et recombiné de façon à faire interférer les deux faisceaux près du miroir séparateur, un déplacement de franges d’interférences est observé lorsqu’on modifie la vitesse de rotation.

Pour les détails sur l’effet Sagnac voir :

http://www.mathpages.com/rr/s2-07/2-07.htm

Cet effet fut remarqué par Sagnac en 1913, et est appelé effet Sagnac.

A ceux qui pourraient penser, que du fait des «  accélérations » rencontrées dans ce problème la Relativité Générale s’impose, rappelons que la Relativité Générale est une théorie de la gravitation, qui n’a pas lieu d’être ici.

La Relativité Restreinte est parfaitement adaptée au traitement des effets cinématiques et des accélérations liées à l’utilisation de référentiels en rotation, par exemple, et l’usage du calcul tensoriel n’est pas réservé à la Relativité Générale. Simplement dans ce cas, comme on va traiter de référentiels qui ne sont pas tous inertiels, l’espace «  global » n’est pas Minkowskien, il ne l’est qu’au niveau infinitésimal, ce qui permet d’établir des équations différentielles locales, qui par intégration nous donnera la solution globale.

2. Premières considérations

L’effet Sagnac, qui a été largement vérifié en Laboratoire, une expérience ayant même utilisé la Terre, elle même, comme corps en rotation, paraît être le point le plus délicat soulevé dans l’introduction.

Ce point a fait couler beaucoup d’encre. Malykin [6] a passé en revue les communications sur le sujet et on peut considérer que le point est résolu.

Mon intention dans ce document n’est pas d’expliquer l’effet Sagnac (cela a été fait), mais plutôt de clarifier ou d’expliquer les paradoxes concernant ce sujet.

Le premier contre argument, est que la RR ne s’applique pas à un disque en rotation, la célérité de la lumière étant localement anisotropique sur le disque et que l’addition galiléenne des vitesses est valide dans ce cas.

Au moins un auteur [7] a été jusqu’à reconstruire une cinématique du disque en rotation à partir du postulat d’addition des vitesses galiléen en suivant la méthode qu’avait utilisé Einstein pour établir la RR. Il peut paraître surprenant de trouver cela dans la littérature, mais en fait ce point de vue est encore enraciné dans certains esprits.

Nous ne partageons pas cette approche qui nous paraît physiquement inconsistante. Notre objectif est d’utiliser un ensemble d’axiomes valables dans tous les référentiels.

Avoir des théories différentes pour décrire les mouvements rectilignes et en rotation, nous paraît épistémologiquement pas souhaitable.

Les confirmations expérimentales de RR nous incitent par ailleurs à bien réfléchir avant d’abandonner cette théorie à la première difficulté rencontrée, au profit d’une autre théorie ad hoc.

Comme indiqué avant, Einstein considéra le problème. Avec d’autres physiciens éminents, déclara que la circonférence C était telle que :

Il considéra que la circonférence dans le référentiel, fixe C0, et la circonférence du disque en rotation C étaient géométriquement équivalentes. Comme les règles étalon, à la périphérie du disque subissaient une contraction de Lorentz, selon la formule habituelle, alors la mesure de la circonférence vaut :

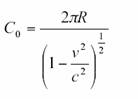
Ceci ne l’a pas inquiété outre mesure. Il fit l’hypothèse que le disque devait se plier et se courber de sorte à satisfaire la contraction de Lorentz.

Nous reviendrons sur ce point plus loin.

3. Circonférence mesurée par différents observateurs

Demandons nous ce qu’un observateur solidaire du disque, situé à sa périphérie, mesure comme circonférence. Supposons qu’on a disposé sur le disque, des règles et des horloges, en chaque point, synchronisées comme on sait le faire en RR. Du point de vue de l’observateur immobile au centre O, un point A à la périphérie se déplace à une vitesse , il va donc mesurer que la longueur infinitésimale d’une portion de la périphérie vaut :

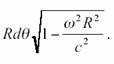
Cette contraction n’est pas physique, cependant car elle dépend de l’observateur. L’observateur sur le disque, à la périphérie, ne va pas observer de contraction localement (dans son voisinage immédiat).

Il va constater que son référentiel «  instantané » se déplace à la vitesse par rapport à O immobile, mais va mesurer que la même petite portion de périphérie vaut

Supposons que l’observateur regarde un autre point B de la circonférence tel que l’angle AÔB = . Pour un observateur en O, le point A, a une vitesse de : et le point B a une vitesse de

{ i et j sont des vecteurs de base orthogonaux attachés au référentiel fixe en O, la situation est représentée sur la figure 1A}

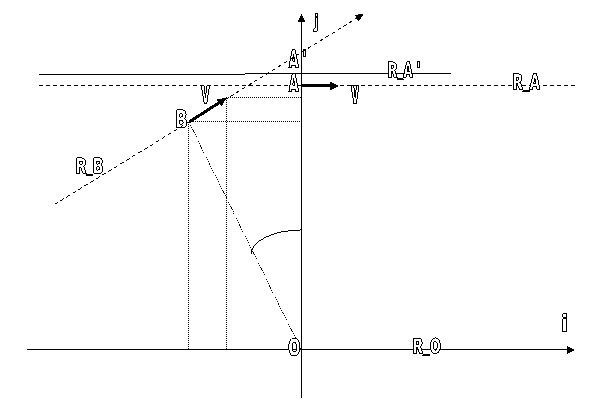
Figure 1A

Diagramme du point de vue de l’observateur en O fixe, les différents référentiels locaux inertiels impliqués sont :

- R_0, celui attaché à O fixe

- R_A, Celui attaché à A, animé d’une vitesse V par rapport à R_O

- R_B, Celui attaché à B animé d’une vitesse par rapport à R_O, et à R_A

- R_A’, Celui attaché à A’, le vis à vis de A, mais à l’extérieur du disque, fixe par rapport à R_O.

Il y a des référentiels partout. Le risque de se tromper est maximum. Sans compter qu’on va devoir intégrer pour trouver la solution globale. Pour faire un calcul béton, il est naturel de raisonner en prenant comme point de départ la description depuis le référentiel fixe situé en O, au moins là les choses sont claires, puisque c’est à partir de là qu’on a défini le problème, et si on garde R et théta comme variables, on sait que le domaine d’intégration est pour théta de 0 à 2pi. Ensuite, on calculera à partir des formules de Lorentz, dont on établira de façon indiscutable le paramètre « v », en bétonnant comme précédemment, les longueurs et temps dans les autres référentiels, à partir de ces variables initiales. Les mathématiques nous garantissant que l’intégrité de notre approche est conservée.

C’est lourd, mais c’est à ce prix qu’on pourra se fier au résultat obtenu ; m^me s’il nous surprend !

La méthode va consister à évaluer la vitesse de R_B par rapport à R_O,.

Puis par changement de référentiel,R_O vers R_A ( on connaît les vitesses relatives), calculer la vitesse de R_B par rapport à R_A.

Cette vitesse va permettre de déterminer le facteur de contraction de Lorentz à appliquer entre les référentiels R_B, et R_A.

On en connaît la valeur mesurée de l’élément différentiel, par l’observateur dans son référentiel, c’est R.d(théta).

En intégrant sur théta de 0 à 2pi, on va trouver le calcul de la longueur de la « circonférence » (périmètre serait plus correct, car la géométrie est déformée pour cet observateur) de la périphérie du disque vue par cet observateur A, depuis le bord du disque en rotation (on conçoit que la géométrie du cercle est déformée).

On peut alors aussi calculer cette longueur telle que mesurée par l’observateur A’ (référentiel A’),ce qui est fait dans la formule (2.6) puisqu’on connaît la vitesse relative de A et A’, c’est , V, donc le facteur de contraction associé : racine ( 1-v²/c²) .

Arrivé à ce stade, de la démonstration, il est recommandé de prendre une aspirine !

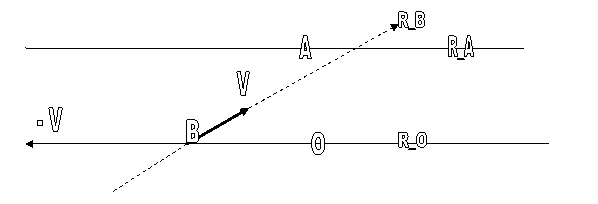
Figure 1B

Le point de vue depuis le référentiel inertiel local attaché à A, considéré comme fixe, montre la transformation à effectuer,( la composition des vitesses vue de R_A), pour obtenir la vitesse de R_B dans R_A, ici R_A’ n’a pas été représenté

Si je transpose cela dans le référentiel de A (que je distingue en le notant avec des « ‘ » ), nous trouvons que l’observateur en A mesure les composantes suivantes pour la vitesse.

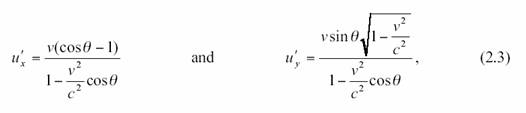
où nous avons posé Alors :

{ En fait on peut directement appliquer la formule de composition des vitesses établie par Einstein en 1905 qui est relatée ci dessous en 2.4, en notant qu’on se place dans le référentiel R_A et que la composition des vitesses est celle de l’observateur fixe attaché à O qui a une vitesse – V par rapport à R_A et celle de l’observateur en B qui va faire un angle pi – théta avec la vitesse de O }

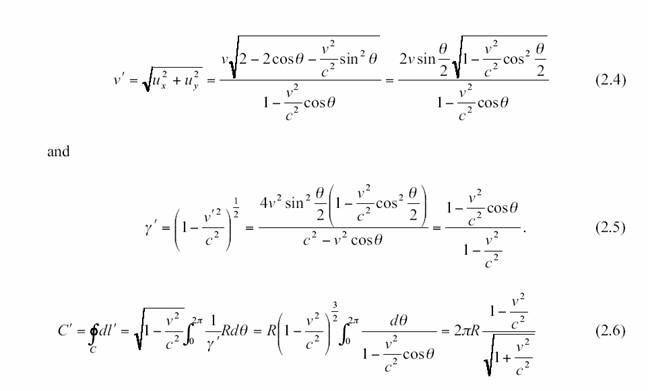
{Errata : Dans la formule (2.5), premier terme qui suit le premier signe = , lire (1-v’²/c²)^{- ½} , au lieu de (1-v’²/c²) ^½. }

La formule (2.6) est établie dans le référentiel R_A’, (au repos par rapport à l’observateur O ), attaché à l’observateur A’ qui mesure la « circonférence » du disque en rotation, puisqu’il tient compte de la contraction de longueur liée à son mouvement par rapport à l’observateur A.

Dans le référentiel R_A attaché à l’observateur A sur le disque, on trouve le calcul à la fin du chapitre 6,( il faut diviser par le facteur de contraction de Lorentz associé à V

Comparons cette circonférence à celle mesuré par l’observateur fixe, en O

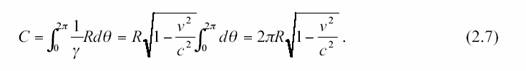
Nous voyons que Ce que vont mesurer les observateurs va dépendre de leur position sur le disque, et ils ne seront pas d’accord sur la valeur de la circonférence.

Manifestement, leur perception variée de ce qu’est la circonférence montre qu’elles ne sont pas géométriquement équivalentes contrairement à ce que Lorentz, Ehrenfest et quelques autres {dont Einstein} prétendaient.

Là, vous pouvez reprendre une aspirine, si nécessaire.

4. Courbure sur le disque

Demandons nous s’il possède une courbure gaussienne ( intrinsèque). Compte tenu de la symétrie du problème, on est incité à travailler en coordonnées cylindriques.

Partons d’un espace temps plat.

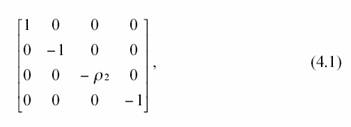
Où, et

Pour un observateur situé à l’origine ( en O), la transformation de coordonnées entre le référentiel inertiel de départ et un référentiel attaché au disque tournant à vitesse angulaire constante oméga est ( immédiatement) donné par

En utilisant l’invariance de l’intervalle d’espace temps

où est le temps propre d’une particule au repos dans le référentiel, et

nous trouvons que

on peut en synthétiser la métrique des coordonnées « ‘ » dans le tableau suivant

Supposons que :

comme c’est le cas pour un point au repos, en particulier sur la circonférence du disque, nous trouvons :

Ceci est la dilatation temporelle de Lorentz classique. Calculons le tenseur métrique inverse

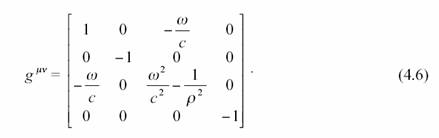
Avec tout cela, on peut calculer les symboles de Christoffel par la formule :

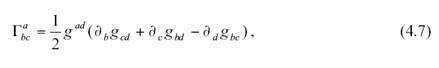
où est l’abréviation de , Ils valent :

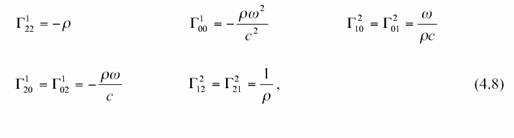
Tous les autres symboles sont nuls.

En utilisant (4.7) ou (4.8) on peut calculer et vérifier que le tenseur de Riemann 0, ce qui montre que l’espace est plat, ce qui n’est pas surprenant , puisqu’on l’a choisi plat au départ et qu’on n’a fait que le décrire dans un autre système de coordonnées. Les équations du champ en Relativité générale stipulent que seule la présence de matière- énergie ( un champ électromagnétique fait l’affaire) est capable de déformer l’espace temps en un système fermé, et dans l’analyse , le disque a été supposé implicitement , sans masse infiniment fin et tournant à vitesse constante.

Cependant on peut séparer l’espace temps en espace et en temps. Considérons deux points sur le disque A et B séparés par une faible distance dxi ( i = 1,2,3) . Une règle attachée à A, à la limite de la séparation tendant vers zéro, va pratiquement être au repos par rapport à B.

On peut séparer les parties spatiales et temporelles ( Landau – Lifchitz théorie des champs [10])

Bien entendu cette séparation n’est valable que localement. Le Landau Lifchitz donne la partie spatiale de comme suit :

En reportant la métrique précédente dans cette formule on obtient pour la métrique spatiale :

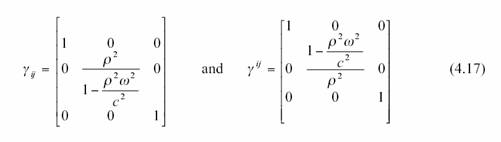
et pour les symboles de Christoffel

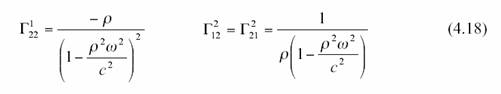
Tous les autres symboles sont nuls. Alors l’équation géodésique devient

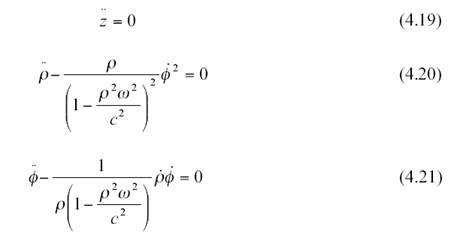
A partir du tenseur métrique de la partie spatiale ( 3D), permettant de calculer le dl², le Landau Lifchitz fait observer que si on fait dz = dr = 0,) et qu’on intègre de 0 à 2pi, on trouve que la longueur de la « circonférence » ainsi calculée est supérieure à 2 pi.R, ( c’est très simple à vérifier) ce qui caractérise une courbure négative. Calculons la courbure directement. Rappelons que le scalaire de courbure ( scalaire de Ricci) est défini par :

et le tenseur de Ricci par

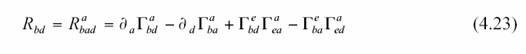
L’opposé du scalaire de courbure vaut :

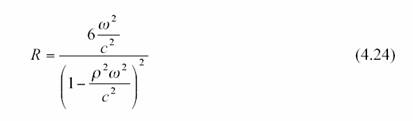
L’opposé de ce scalaire est toujours positif, ce qui fait que le scalaire de courbure est toujours négatif, comme la remarque du Landau Lifchitz le laissait entendre. Ceci paraît en contradiction avec les résultats que nous avons trouvés à la fin du chapitre 2. Alors quoi ! La Relativité Restreinte nous t’elle raconte n’importe quoi ?

Que nenni !

D’abord, il s’agit d’une courbure spatiale intrinsèque 3D et non pas une courbure extrinsèque 2D, comme on est tenté de se la représenter.

En fait le résultat trouvé ici n’est pas en contradiction avec les formules (2.4)-(2.6), s’agissant de choses différentes, car évaluées dans des référentiels différents.

Le scalaire de Ricci 4D est lui invariant par toutes les transformations de coordonnées puisque c’est un scalaire,( d’ailleurs dans notre cas , il est nul), mais pas le scalaire de Ricci de la partie spatiale seulement qui dépend du référentiel choisi..Pour s’en persuader, il suffit de le calculer dans le système de référence, représentant le même espace temps, dont on est parti, il est nul dans ce cas ( tous les symboles de Christoffel sont nuls).

Ce point est important si on veut y comprendre quelque chose. (Une troisième aspirine ?)

5. Synchronisme sur la circonférence du disque.

L’effet Sagnac, et en fait toutes les menues contrariétés que nous avons endurées tout au long de ce document, ont leur source dans l’impossibilité de synchroniser les horloges sur le disque en utilisant la seule méthode possible, permettant aux observateurs de s’accorder, celle définie en Relativité Restreinte. Dans l’introduction nous vous avions déjà signalé la non transitivité de la procédure de synchronisation à la périphérie du disque. Evaluons ce défaut de synchronisation.

Imaginons deux évènements A et B, simultanés dans un référentiel K, attaché à la périphérie du disque en rotation, séparé par une distance dx. Regardons ce qui se passe du point de vue d’un référentiel adjacent K’ (fixe) :

On peut évaluer le temps séparant A et B dans le référentiel K’ par les transformations de Lorentz.

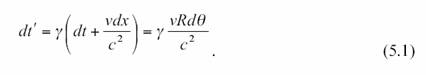
{ Attention ! « dt ’ », est le temps « dt » qui s’écoule sur le référentiel en rotation ( le disque) mais évalué par un observateur «  fixe » attaché au référentiel K’. Si le disque a une vitesse «  v » par rapport au référentiel « fixe », la vitesse relative de K’ par rapport à K est alors de – v, d’ou la forme de la formule avec le signe + ( c’est la formule réciproque de la formule de base). Dans ce cas, gamma = racine de ( 1-v²/c²) grandeur constante , l’intégration sur 2pi est immédiate et donne (5.2)}

Considérons maintenant la différence de temps entre B et C, dans un troisième référentiel infinitésimal et procédons ainsi de proche en proche tout le long de la circonférence du disque. En intégrant la vitesse de 0 à on voit qu’il existe une différence de temps lorsqu’on fait le tour du disque.

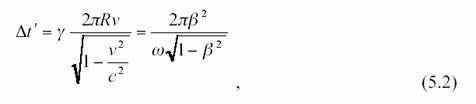
qui est précisément ce qui est mesuré par l’effet Sagnac sous forme de différence de phase entre les faisceaux co et contra rotationnels. [4][5][6]

Nous voyons que la désynchronisation, est fondamentalement une manifestation différente du paradoxe des jumeaux. Comme dans le paradoxe des jumeaux c’est le changement de référentiel qui est à la source de la discordance, bien qu’ici, par rapport, à la version de base ou le demi tour est instantané (mais le demi tour, comme l’accélération de départ et d’arrivée peuvent être également continus, sans que cela ne change le principe dans le paradoxe de Langevin), le changement de référentiel est infinitésimal et continu. Signalons également que la différence de temps entre celui marqué par une horloge qui a voyagé autour du disque et une qui est restée au repos par rapport au disque est un effet objectif (puisqu’on se retrouve au même point, comme dans le cas du paradoxe des jumeaux au retour ). Malgré les désaccords sur la notion de simultanéité des différents observateurs, ceux ci s’accorderont par contre sur la désynchronisation objective qui se produit après un tour.

6.1 De l’objectivité de la courbure spatiale

En l’absence de matière et autres sources gravitationnelles, à ce point on peut se demander après le calcul de la courbure spatiale ( 4.22), d’où elle vient. Est elle «objective» ?.

Dans l’espace à 3+1 dimensions où nous avons nos habitudes de pensée, ce n’est pas très clair, mais dans l’espace temps de la RR à quatre dimensions ce n’est pas ambigu. On peut éclairer le débat en traçant un simple diagramme d’espace temps. Comme le disque est supposé infiniment fin, et que rien ne se produit dans la direction « z » nous pouvons supprimer le troisième dimension et traiter le problème en deux dimensions (spatiales), ce qui permet d’utiliser la dimension libérée pour représenter l’évolution temporelle.

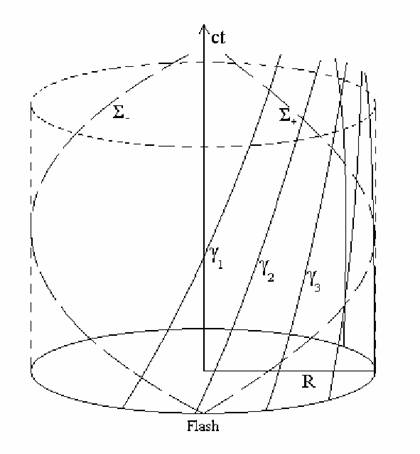
Figure 2

Comme montré sur la figure 2 ci dessus, (empruntée à [5]), les lignes d’univers les points de la périphérie du disque, dénotées , etc.. sont des hélices de type temps, comme de bien entendu, car des particules massives ne peuvent pas aller plus vite que la lumière. Les chemins et associés aux rayons lumineux issus d’un éclair lumineux et se propageant en sens contraire sont aussi des hélices, mais de type lumière comme il se doit, s’enroulant en sens contraire autour tu tube d’univers tracé par le disque. Ceci est en général admis et pas controversé dans la littérature.

Le problème se corse quand on essaie de définir le lieu des «  simultanéités » correspondant à la périphérie du disque. En utilisant la définition de la RR de la simultanéité, les évènements simultanés à un éclair vont être orthogonaux aux lignes d’univers de l’observateur en question (dans ce cas, un observateur chevauchant l’onde électromagnétique produite par l’éclair). L’intégration que nous avons faite au chapitre 5, est vue comme mesurant une courbe ouverte de type espace dans l’espace temps.

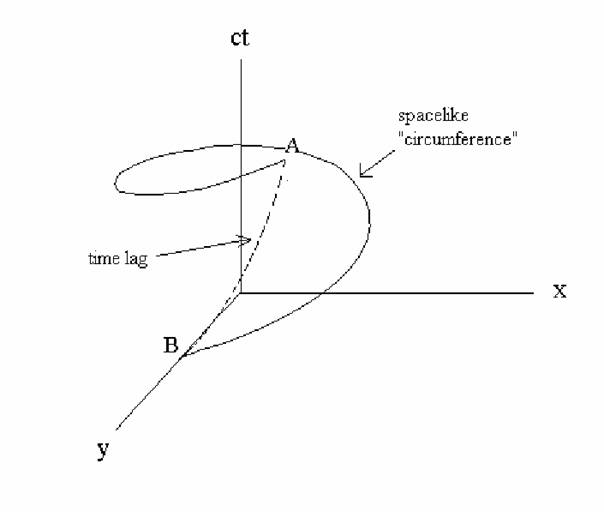
Figure 3

De la figure 3, il ressort que l’extrémité d’un ruban, appliqué sur la périphérie du disque ne va pas rejoindre l’autre extrémité au même point temporel. Les deux extrémités vont être séparées par une ligne d’univers de type temps dont la longueur est donnée par l’équation (5.2). Quand , les lignes d’univers des points à la périphérie du disque, sont des droites et le lieu des évènements simultané à l’éclair est une courbe fermée de type espace.

Mais dès que le disque est mis en rotation, et devient une courbe ouverte, de sorte que la notion de simultanéité devient conventionnelle, dépendant du point de départ de l’intégration effectuée au chapitre 5. Remarquons aussi, qu’en combinant les figures 2 et 3, l’angle que les faisceaux lumineux et font avec les de type temps (dans la figure 2) est égal à l’angle entre les rayons et la «circonférence» (dans la figure 3) : Ceci est évidemment dû au fait que la vitesse de la lumière mesurée dans les référentiels tangents inertiels est la même et égale à « c ».

Alors que ceci est plutôt clair dans l’espace temps 4D, il est moins évident de dire ce que ceci signifie pour un observateur sur le disque.

Considérons un observateur muni, comme d’habitude, d’un nombre infini de minuscules petites règles et de deux horloges identiques synchronisées. Quand il voyage le long du bord du disque, à vitesse non relativiste (par rapport au bord du disque), il dépose ses règles étalons et transporte une horloge avec lui. Lorsqu’il atteint de nouveau son point de départ, il va conclure que la circonférence correspond au nombre de règles étalons qu’il a déposé, soit :

.

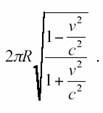Ceci est compatible avec la valeur donnée au (2.6), pour ce que mesure un observateur fixe, juste à la périphérie du disque, qui observe une contraction complémentaire par un facteur de Lorentz lié sa vitesse V relative.

Cependant, il va constater que son horloge retarde par rapport à celle qu’il a laissé sur place d’une valeur donnée par (5.2).

Nous voyons donc, que la courbure obtenue par la méthode suggérée par Moller est résulte du fait qu’on force artificiellement les points A et B dans la figure 4 à être réunis.

On procède à une identification des points représentant les extrémités, comme cela se fait dans les espaces-temps « compacts ». Le disque en rotation est un espace temps compact. Il faut donc prendre en compte ce qu’on appelle « l’holonomie » de la boucle pour que cette indentification liée à la compacité de l’espace se fasse correctement.

Cette remarque s’applique évidemment à toute la classe de problèmes qui mettent en jeu des boucles dans l’espace-temps. Le paradoxe de Langevin par exemple, dans sa version classique possède cette caractéristique. L’holonomie est alors constaté par la différence de temps propre entre les jumeaux.

Formellement ceci peut être vu comme une conséquence du théorème de Stockes :dans une variété Riemannienne la circulation, d’une (n-1)_ forme linéaire M le long d’un contour fermé, délimitant une surface est égal à l’intégrale de surface «  flux » de la n_ forme dérivée dM . Cette intégrale est nulle seulement si la n-1 forme est exacte ou fermée.

7. Conclusion

Comme beaucoup de paradoxes, le paradoxe d’Ehrenfest naît de l’absence de notion de simultanéité absolue en Relativité. Il est clair que la plupart des physiciens qui ont étudié le disque en rotation, ont implicitement supposé que la circonférence du disque en rotation avait une géométrie bien définie. Cependant en s’appuyant sur des diagrammes de Minkowski, plutôt simples, on voit qu’une définition naturelle et cohérente de la simultanéité pour l’ensemble de la périphérie du disque n’est pas possible, ceci étant très caractérisé pour des rotations rapides. Si on décompose l’espace temps en temps et espace, les résultats de calculs ne vont pas permettre une vérification expérimentale (en fait c’est ainsi que la courbure calculée au chapitre 4 apparaît)

Le plus simple est encore de voir les paradoxes du disque en rotation comme une déclinaison du paradoxe des jumeaux. C’est dans le changement incessant de référentiel de référence que le temps se « perd » (et aussi le peu de raison qui reste au courageux qui est arrivé jusque là !) .

Citons Rizzi et Tartaglia [5]

«  Un disque en rotation n’admet pas de « référentiel (global) propre » bien défini. Il faut plutôt regarder cela comme une classe de référentiel constitué d’un nombre infini de référentiels locaux propres considérés aux différents points à différents instants et assemblés selon certaines règles »

[9] http://www.mathpages.com/rr/s2-07/2-07.htm

[10] Landau Lifchitz, : théorie des champs.