La géométrie du disque en rotation, d’après :

http://www.smcm.edu/nsm/physics/SMP03S/KeatingB.doc.pdf

Traduction libre J. Fric, qui endosse toute responsabilité pour toutes les erreurs que sa traduction aurait pu introduire. Commentaires personnels en petits caractères italiques rouges entre { ..}. Ces commentaires n’engagent évidemment que moi…

Date de création du document : le 8 Mars 2004

1-Introduction

L’étude du cas d’un disque rigide en rotation à des vitesses relativistes soulève d’intéressants paradoxes, et fait l’objet de nombreux contresens d’interprétation. La Relativité Restreinte nous enseigne que si on utilise une règle le long de la périphérie d’un tel disque, elle subit la contraction de Lorentz, alors que dans la mesure du rayon, ce n’est pas le cas. On en déduit que le rapport entre la circonférence et le rayon, ainsi mesuré, ne sera pas égal à pi. Ce paradoxe fut présenté pour la première fois par Paul Ehrenfest en 1909 et on l’appelle donc le paradoxe d’Ehrenfest [1].

{Cet effet se produit, bien entendu quelque soit la vitesse de rotation du disque, mais l’ampleur de l’effet devient significative à des vitesses relativistes}

Einstein connaissait ce paradoxe, et y a fait référence dans son article de 1916, pour justifier la nécessité d’introduire des géométries non euclidiennes en Relativité Générale [2]

Mais il n’a jamais proposée une étude complète de ce cas. D’autres physiciens comme Strauss [3] ont fait observer que si les règles étaient contractées (de Lorentz), les objets qu’elles mesuraient l’étaient tout autant, donc que tout cela se compensait et qu’on devait trouver un rapport C/D égal à pi.

Une autre difficulté, qui n’aide pas vraiment à y voir clair, est la non transitivité de l’ordre des événements (posant des problèmes de synchronisation temporelle) le long de la périphérie du disque

{C’est la clé de la compréhension du «  paradoxe »}.

Pour mettre en évidence ce point simplement, considérons seulement 4 référentiels inertiels (instantanés), K1, K2,K3 et K4, parmi l’infinité de référentiels différents possibles.

Voir figure 1

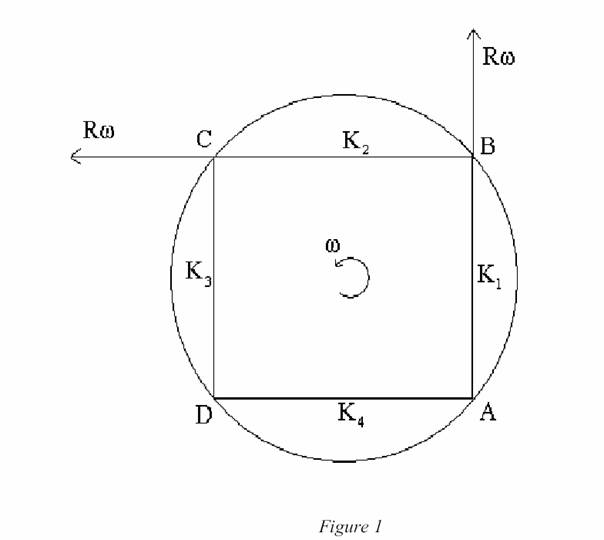
Les lettres A, B, C, D représentent des évènements (disons l’émission d’un éclair) qui se produisent à la périphérie du disque.

Supposons que les évènements A et B soient simultanés dans K1, B et C simultanés dans K2, C et D simultanés dans K4(*).

{ (*)Dans le texte original, il y a écrit K4, je pense que c’est une coquille, et que c’est K3 qu’il faut lire,comme la suite l’indique }

Si A et B sont simultanés dans K1, alors dans K2, lorsqu’on fait la transformation de référentiel K2/K1 on s’aperçoit que A est antérieur à B du fait du mouvement relatif de K1 par rapport à K2 de A vers B

{Quelques mots pour illustrer sans calcul, l’affirmation : La simultanéité s’apprécie dans K1 par le fait qu’un observateur O situé au milieu de AB, va voir les deux éclairs en même temps.

La lumière émise de A, va dans le même sens que le mouvement relatif de K1 par rapport à K2 dans cette direction, cette lumière émise de A, va donc à la rencontre des observateurs de K2, c’est pour cela que A va être vu avant B par les observateurs de K2.Les sceptiques pourront faire le calcul par les formules de Lorentz qui confirment ce point}

De même dans K3, B va être antérieur à C et dans K4, C va être antérieur à D,

{ jusque là rien dire}

finalement en faisant la transformation qui nous ramène à notre point de départ, le référentiel K1, on voit que A est antérieur à D(*).

Donc en faisant le tour du disque via les quatre référentiels, on voit que A se produit avant B, qui se produit avant C, qui se produit avant D, qui se produit avant A(**).

Apparemment, une discontinuité dans le temps s’est produite, et il y a un os dans le potage.

{ Là, notre ami se prend carrément les pieds dans le tapis, en se contredisant entre (*) et (**) Moi, je ne vois pas comment il peut affirmer (**), car ce serait supposer que D et A sont simultanés dans K4, si on suit la même logique, mais on n’a pas la liberté d’imposer ce choix, on a déjà utilisé tous les degrés de libertés, disons que cela montre la relativité de la simultanéité,et que dans le cas d’un circuit fermé comme celui là, on ne peut pas respecter de « symétrie cyclique» comme la nature du problème incite à le faire. Lorsqu’on revient à son point de départ, ce défaut est bien mis en évidence puisqu’on ne peut pas continuer le même procédé, le supposer conduit à une contradiction }

{Cela peut donner quelques migraines, aux tenants de l’espace absolu, mais les Relativistes savent, qu’en relativité la notion de simultanéité dépend du référentiel dans lequel on considère les évènements}

Un paradoxe plus fondamental et plus troublant a été proposé par Selleri dans l’article cité en référence [4].

Par un raisonnement élémentaire, on peut montrer, en supposant seulement que la circonférence du disque a une géométrie bien définie, que le rapport de la vitesse apparente de lumière en contre- rotation et co-rotation est donné par

où est la vitesse angulaire supposée constante, et R le rayon du disque, avec

,

et c+ et c- sont les vitesses de la lumière en co-rotation et contre rotation respectivement.

Le paradoxe se produit quand : et dans l’équation, (1.1).

Alors l’accélération centrifuge :, et ceci, même, si on garde la vitesse tangentielle constante :

Le référentiel associé au bord du disque tend vers un référentiel inertiel, se déplaçant à la vitesse :

par rapport à un observateur au centre, attaché au référentiel fixe.

Ceci crée une discontinuité, car on sait que dans un référentiel inertiel la vitesse de la lumière est la même dans les deux sens :, alors que la formule (1.1) qui reste invariante, du fait de l’invariance de « v » par ce passage à la limite indique une valeur très différente.

Il y a des confirmations de l’apparente anisotropie de la vitesse de la lumière sur un disque en rotation. Si un faisceau laser ( cohérent) est fractionné en deux faisceaux (cohérents) se déplaçant en sens contraire sur le disque sur la périphérie d’un disque en rotation rapide (au moyen de miroirs semi transparents par exemple) et recombiné de façon à faire interférer les deux faisceaux près du miroir séparateur, un déplacement de franges d’interférences est observé lorsqu’on modifie la vitesse de rotation. La différence de temps d’arrivée entre les deux faisceaux [5] est donnée par

{ Le temps que met la lumière pour faire un tour en co-rotation, moins le temps pour faire un tour en contra-rotation vaut le double de la valeur donnée par la formule (1.2) ci dessus. Par ailleurs, précisons que cette valeur est évaluée dans le référentiel «  repos »}

Cet effet fut remarqué par Sagnac en 1913, et est appelé effet Sagnac.

Certains pourraient penser, que du fait des «  accélérations » rencontrées dans ce problème la Relativité Générale s’impose. Rappelons que la Relativité Générale est une théorie de la gravitation, qui n’a pas lieu d’être ici.

La Relativité Restreinte est parfaitement adaptée au traitement des effets cinématiques et des accélérations liées à l’utilisation de référentiels en rotation, par exemple, et l’usage du calcul tensoriel n’est pas réservé à la Relativité Générale. Simplement dans ce cas, comme on va traiter de référentiels qui ne sont pas tous inertiels, l’espace «  global » n’est pas Minkowskien, il ne l’est qu’au niveau infinitésimal, ce qui permet d’établir des équations différentielles locales, qui par intégration nous donnera la solution globale.

2. Premières considérations

L’effet Sagnac, qui a été largement vérifié en Laboratoire, une expérience ayant même utilisé la Terre, elle même, comme corps en rotation, paraît être le point le plus délicat soulevé dans l’introduction.

Ce point a fait couler beaucoup d’encre. Malykin [6] a passé en revue les communications sur le sujet et on peut considérer que le point est résolu.

Mon intention dans ce document n’est pas d’expliquer l’effet Sagnac (cela a été fait), mais plutôt de clarifier ou d’expliquer les paradoxes concernant ce sujet.

Le premier contre argument, est que la RR ne s’applique pas à un disque en rotation, la célérité de la lumière étant localement anisotropique sur le disque et que l’addition galiléenne des vitesses est valide dans ce cas.

Au moins un auteur [7] a été jusqu’à reconstruire une cinématique du disque en rotation à partir du postulat d’addition des vitesses galiléen en suivant la méthode qu’avait utilisé Einstein pour établir la RR. Il peut paraître surprenant de trouver cela dans la littérature, mais en fait ce point de vue est encore enraciné dans certains esprits.

Nous ne partageons pas cette approche qui nous paraît physiquement inconsistante. Notre objectif est d’utiliser un ensemble d’axiomes valables dans tous les référentiels.

Avoir des théories différentes pour décrire les mouvements rectilignes et en rotation, nous paraît épistémologiquement pas souhaitable.

Les confirmations expérimentales de RR nous incitent par ailleurs à bien réfléchir avant d’abandonner cette théorie à la première difficulté rencontrée, au profit d’une autre théorie ad hoc.

Comme indiqué avant, Einstein considéra le problème. Avec d’autres physiciens éminents, déclara que la circonférence C était telle que :

Il considéra que la circonférence dans le référentiel, fixe C0, et la circonférence du disque en rotation C étaient géométriquement équivalentes. Comme les règles étalon, à la périphérie du disque subissaient une contraction de Lorentz, selon la formule habituelle, alors la mesure de la circonférence vaut :

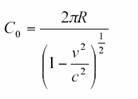
Ceci ne l’a pas inquiété outre mesure. Il fit l’hypothèse que le disque devait se plier et se courber de sorte à satisfaire la contraction de Lorentz.

Indépendamment du côté ad hoc de l’hypothèse, de telles contorsions violeraient la symétrie supposée du problème. Si le disque était courbé dans la direction verticale (z+ ou z-) il induirait une dissymétrie dans cette direction et violerait la symétrie de parité spatiale des référentiels inertiels.

{Examiner la portée de l’argument. Il faut noter que la courbure calculée à la fin du chapitre 4 est une courbure 3D. L’argument cité ci dessus se rapporte plutôt à une courbure 2D. Est il exclu d’avoir une courbure qui ne viole pas la symétrie de parité ?. Je serai tenté de mettre cet argument entre parenthèses.}

3. Circonférence mesurée par différents observateurs

Demandons nous ce qu’un observateur, au repos par rapport à la périphérie du disque, mesure comme circonférence. Supposons qu’on a disposé sur le disque, des règles et des horloges, en chaque point, synchronisées comme on sait le faire en RR . Du point de vue de l’observateur immobile au centre O, un point A à la périphérie se déplace à une vitesse , il va donc mesurer que la longueur infinitésimale d’une portion de la périphérie vaut :

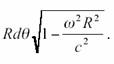
Cette contraction n’est pas physique, cependant car elle dépend de l’observateur. L’observateur à la périphérie, ne va pas observer de contraction localement (dans son voisinage immédiat).

Il va constater que son référentiel «  instantané » se déplace à la vitesse par rapport à O immobile , mais va mesurer que la même petite portion de périphérie vaut

Supposons que l’observateur regarde un autre point B de la circonférence tel que l’angle AÔB = . Pour un observateur en O, le point A, a une vitesse de : et le point B a une vitesse de

{ i et j sont des vecteurs de base orthogonaux attachés au référentiel fixe en O}

Figure 1A

{ Diagramme du point de vue de l’observateur en O fixe, les différents référentiels locaux inertiels impliqués sont :

- R_0, celui attaché à O fixe

- R_A, Celui attaché à A, animé d’une vitesse V par rapport à R_O

- R_B, Celui attaché à B animé d’une vitesse par rapport à R_O, et à R_A

- R_A’, Celui attaché à A’, le vis à vis de A, mais à l’extérieur du disque, fixe par rapport à R_O.}.

{ la méthode va consister à la vitesse de R_B par rapport à R_O.

Puis par changement de référentiel,R_O vers R_A ( on connaît les vitesses relatives), calculer la vitesse de R_B par rapport à R_A.

Ceci va permettre de déterminer le facteur de contraction de Lorentz des longueurs de R_B, mesurées localement par l’observateur B, (on en connaît la valeur c’est R.d(théta) ), telles que les mesure l’observateur A dans son référentiel R_A, permettant par intégration le calcul de la longueur de la circonférence de la périphérie du disque vue par cet observateur A, depuis le bord du disque en rotation ( on conçoit que la géométrie du cercle est déformée).

On peut alors aussi calculer cette longueur telle que mesurée par l’observateur A’ ( référentiel A’),ce qui est fait dans la formule (2.6) puisqu’on connaît la vitesse relative de A et A’, c’est , V, donc le facteur de contraction associé : racine ( 1-v²/c²) }.

Figure 1B

{Le point de vue depuis le référentiel inertiel local attaché à A, considéré comme fixe, montre la transformation à effectuer,( la composition des vitesses vue de R_A), pour obtenir la vitesse de R_B dans R_A, ici R_A’ n’a pas été représenté}

Si je transpose cela dans le référentiel de A (que je distingue en le notant avec des « ‘ » ), nous trouvons que l’observateur en A mesure les composantes suivantes pour la vitesse.

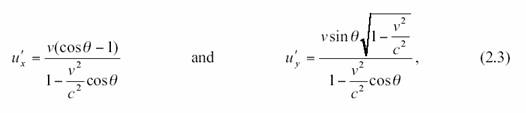
où nous avons posé Alors :

{ En fait on peut directement appliquer la formule de composition des vitesses établie par Einstein en 1905 qui est relatée ci dessous en 2.4, en notant qu’on se place dans le référentiel R_A et que la composition des vitesses est celle de l’observateur fixe attaché à O qui a une vitesse – V par rapport à R_A et celle de l’observateur en B qui va faire un angle pi – théta avec la vitesse de O }

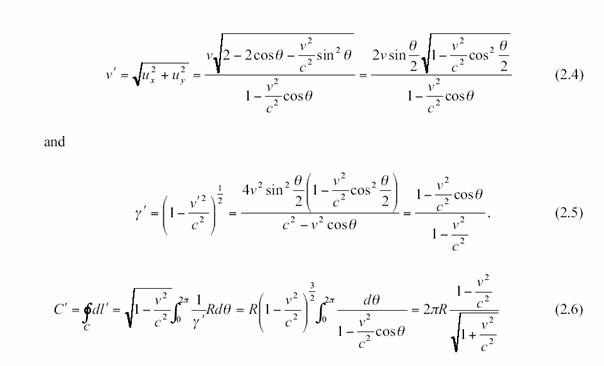
{ Dans la formule (2.5) en fait, le premier terme à droite doit être à la puissance – ½ et non pas +1/2. Après c’est correct. Dans la formule (2.6) le terme racine de (1 -v²/c²), dans l’intégrale, me semble parachuté, avec les notations de la figure 1A, je suppose que ce terme doit signifier que c’est l’observateur A’ qui mesure la circonférence (au repos par rapport à l’observateur O ), puisqu’il tient compte de la contraction de longueur liée à son mouvement par rapport à l’observateur A. Si l’observateur A sur le disque, mesure la périphérie du disque, sur le disque en rotation lui même, ce qui est évalué à la fin du chapitre 6, il éliminer ce facteur ce facteur }

Comparons cette circonférence à celle mesuré par l’observateur fixe, en O

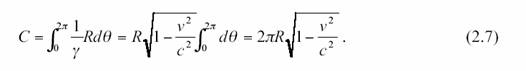
Nous voyons que Ce que vont mesurer les observateurs va dépendre de leur position sur le disque, et ils ne seront pas d’accord sur la valeur de la circonférence.

Manifestement, leur perception variée de ce qu’est la circonférence montre qu’elles ne sont pas géométriquement équivalentes contrairement à ce que Lorentz, Ehrenfest et quelques autres {dont Einstein ?} prétendaient.

4. Courbure sur le disque

En dépit de la violation de symétrie de parité, compte tenu de l’apparente nature non Euclidienne de la surface d’un disque en rotation rapide, demandons nous s’il possède une courbure gaussienne ( intrinsèque). Compte tenu de la symétrie du problème, on est incité à travailler en coordonnées cylindriques.

Partons d’un espace temps plat.

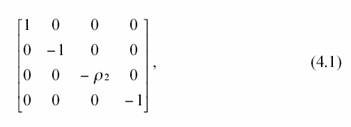
Où, et

Pour un observateur situé à l’origine ( en O), la transformation de coordonnées entre le référentiel inertiel de départ et un référentiel attaché au disque tournant à vitesse angulaire constante oméga est ( immédiatement) donné par

En utilisant l’invariance de l’intervalle d’espace temps

où est le temps propre d’une particule au repos dans le référentiel, et

nous trouvons que

on peut en synthétiser la métrique des coordonnées « ‘ » dans le tableau suivant

Supposons que :

comme c’est le cas pour un point au repos, en particulier sur la circonférence du disque, nous trouvons :

Ceci est la dilatation temporelle de Lorentz classique. Calculons le tenseur métrique inverse

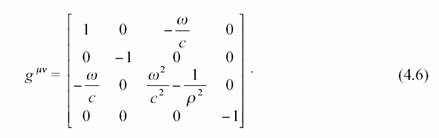
Avec tout cela, on peut calculer les symboles de Christoffel par la formule :

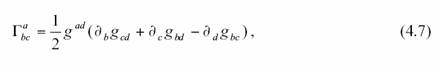
où est l’abréviation de , Ils valent :

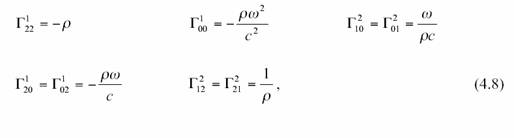
{ j’en ai vérifié un au hasard, c’est bon}

Tous les autres symboles sont nuls. Si on transforme cela en coordonnées cartésiennes, on trouve :

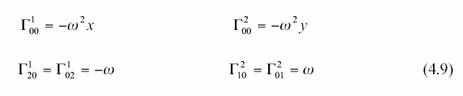
{ A priori, je ne voit pas l’intérêt de faire cela, pourquoi ne pas considérer l’équation géodésique en coordonnées cylindriques qui paraissent mieux adaptées. A par cela ce qui suit ressemble à ce qu’on s’attend à trouver}

Utilisons les dans l’équation géodésique des espaces courbes.

Nous obtenons les géodésiques exprimées en coordonnées cartésiennes sur le disque en rotation.

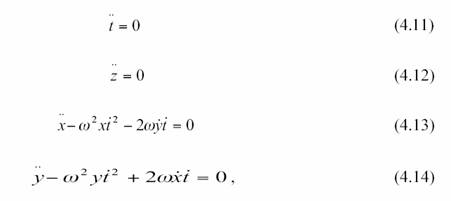
où les points dénotent la différentiation ( jouent le rôle des « ‘ ») par rapport à un paramètre affine de la courbe (typiquement de temps propre). L’équation (4.11) implique que t’ = constante. Utilisant cette propriété, en multipliant par la masse m de la particule, on peut réécrire les équations (4.12)-(4.14) comme suit :

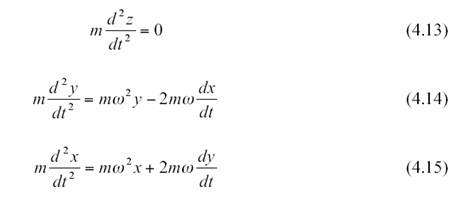
ou en utilisant la notation vectorielle 3 D

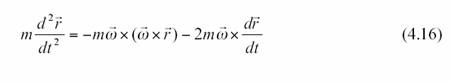
Ce qui l’équation du mouvement d’une particule libre dans un référentiel en rotation uniforme. On voit qu’un observateur qui utilise la coordonnée t comme temps «ressent » des pseudo- forces centrifuge et de Coriolis. Remarquons que ces pseudo-forces ( la gravitation, sil y en avait, en serait aussi) sont implicitement la manifestation de la présence de dérivées secondes de la métrique dans l’équation du mouvement.

En utilisant (4.7) ou (4.8) on peut calculer et vérifier que le tenseur de Riemann 0, ce qui montre que l’espace est plat, ce qui n’est pas surprenant , puisqu’on l’a choisi plat au départ et qu’on n’a fait que le décrire dans un autre système de coordonnées. Les équations du champ en Relativité générale stipulent que seule la présence de matière- énergie ( un champ électromagnétique fait l’affaire) est capable de déformer l’espace temps en un système fermé, et dans l’analyse , le disque a été supposé implicitement , sans masse infiniment fin et tournant à vitesse constante.

Cependant on peut séparer l’espace temps en espace et en temps. Considérons deux points sur le disque A et B séparés par une faible distance dxi ( i = 1,2,3) . Une règle attachée à A, à la limite de la séparation tendant vers zéro, va pratiquement être au repos par rapport à B.

On peut séparer les parties spatiales et temporelles ( voir Moller [8]).

{ On peut aussi voir, Landau Lifchitz,, et cela donne la même chose , et c’est du béton }

Bien entendu cette séparation n’est valable que localement. Moller donne la partie spatiale de comme suit :

En reportant la métrique précédente dans cette formule on obtient pour la métrique spatiale :

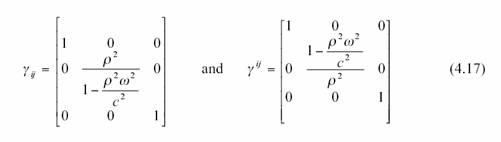
et pour les symboles de Christoffel

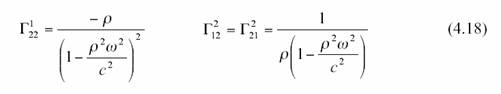
{ Comme tout à l’heure j’en ai vérifié un, c’est bon)

Tous les autres symboles sont nuls. Alors l’équation géodésique devient

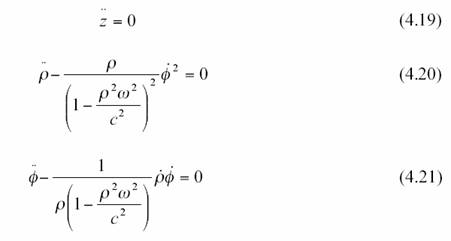
Là, Moller calcule la somme des angles internes d’un triangle définis par de telles géodésiques, et utilise le résultat pour en déduire la courbure gaussienne, mais il est plus classique de calculer la courbure directement, ce que nous faisons. Rappelons que le scalaire de courbure ( scalaire de Ricci) est défini par :

et le tenseur de Ricci par

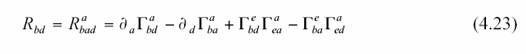
le scalaire de courbure vaut :

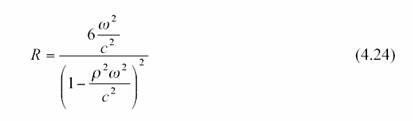
Il est toujours positif, comme dans le cas d’une sphère. Ceci est cohérent avec le fait que sur une sphère la circonférence est inférieure à , par un facteur qui dépend de la position de l’observateur.

{Calculer le scalaire de courbure est une méthode béton pour évaluer la courbure. J’ai calculé ce scalaire, je le trouve égal à l’opposé de ce qui est indiqué ici (même valeur absolue, signe «  moins », donc je trouve une courbure négative). Le résultat de mon calcul est en accord avec les indications du Landau Lifchitz, obtenues à partir de considérations directes sur la métrique, qui est exactement la même, la courbure intrinsèque 3D spatiale est négative. Attention, il s’agit d’une courbure spatiale intrinsèque 3D et non pas 2D Je pense que l’auteur se trompe ici. Le commentaire qui suit est naturellement erroné..Je pense qu’il voulait justifier les résultats obtenus au chapitre 2, notamment par les formules (2.4)-(2.7). En fait le résultat trouvé ici n’est pas en contradiction avec ces formules, s’agissant de choses différentes et étant évaluées dans des référentiels différents. Le scalaire de Ricci 4D est lui invariant par toutes les transformations de coordonnées puisque c’est un scalaire,( d’ailleurs dans notre cas , il est nul) mais pas le scalaire de Ricci de la partie spatiale seulement qui dépend du réfrentiel choisi... Ce point est important si on veut y comprendre quelque chose. D’ailleurs l’auteur semble succomber à cette confusion, puisqu’il s’interroge sur la «  réalité » de cette courbure spatiale qui essaie d’évacuer par des arguments parfois laborieux et où il n’évite pas des «  contradictions » }

5. Synchronisme sur la circonférence du disque.

L’effet Sagnac, et en fait toutes les menues contrariétés que nous avons endurées tout au long de ce document, ont leur source dans l’impossibilité de synchroniser les horloges sur le disque en utilisant la seule méthode possible, permettant aux observateurs de s’accorder, celle définie en Relativité Restreinte. Dans l’introduction nous vous avions déjà signalé la non transitivité de la procédure de synchronisation à la périphérie du disque. Evaluons ce défaut de synchronisation.

Imaginons deux évènements A et B, simultanés dans un référentiel K, attaché à la périphérie du disque en rotation, séparé par une distance dx. Regardons ce qui se passe du point de vue d’un référentiel adjacent K’ (fixe) :

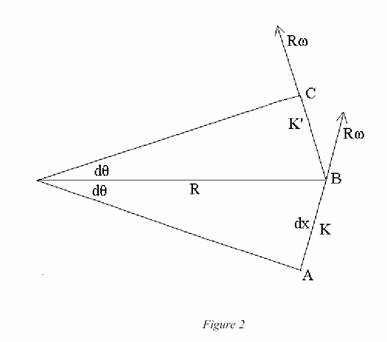
On peut évaluer le temps séparant A et B dans le référentiel K’ par les transformations de Lorentz.

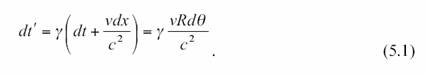
{ Attention ! « dt ’ », est le temps « dt » qui s’écoule sur le référentiel en rotation ( le disque) mais évalué par un observateur «  fixe » attaché au référentiel K’. Si le disque a une vitesse «  v » par rapport au référentiel « fixe », la vitesse relative de K’ par rapport à K est alors de – v, d’ou la forme de la formule avec le signe + ( c’est la formule réciproque de la formule de base). Dans ce cas, gamma = racine de ( 1-v²/c²) grandeur constante , l’intégration sur 2pi est immédiate et donne (5.2)}

Considérons maintenant la différence de temps entre B et C, dans un troisième référentiel infinitésimal et procédons ainsi de proche en proche tout le long de la circonférence du disque. En intégrant la vitesse de 0 à on voit qu’il existe une différence de temps lorsqu’on fait le tour du disque.

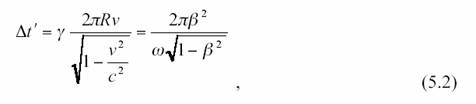
qui correspond précisément à la moitié ( du fait qu’on ne fait pas interférer des faisceaux en sens contraire) de ce qui est mesuré par l’effet Sagnac sous forme de différence de phase entre les faisceaux co et contra rotationnels. [4][5][6]

Nous voyons que la désynchronisation, est fondamentalement une manifestation différente du paradoxe des jumeaux. Comme dans le paradoxe des jumeaux c’est le changement de référentiel qui est à la source de la discordance, bien qu’ici, par rapport, à la version de base ou le demi tour est instantané (mais le demi tour, comme l’accélération de départ et d’arrivée peuvent être également continus, sans que cela ne change le principe), le changement de référentiel est infinitésimal et continu. Signalons également que la différence de temps entre celui marqué par une horloge qui a voyagé autour du disque et une qui est restée au repos par rapport au disque est effet objectif (puisqu’on se retrouve au même point, comme dans le cas du paradoxe des jumeaux au retour). Malgré les désaccords sur la notion de simultanéité des différents observateurs, ceux ci s’accorderont par contre sur la désynchronisation objective qui se produit après un tour.

6.1 Sources de courbure

En l’absence de matière et autres sources gravitationnelles, à ce point on peut se demander après le calcul de la courbure spatiale ( 4.22), d’où elle vient. Est elle «réelle» ?.

{ Voir commentaires fin du chapitre 4 : Elle dépend du système de coordonnées choisie, elle n’a pas de caractère courbure géométrique invariante, au sens d’une courbure espace temps)

Dans l’espace à 3+1 dimensions où nous avons nos habitudes de pensée, ce n’est pas très clair, mais dans l’espace temps de la RR à quatre dimensions ce n’est pas ambigu. On peut éclairer le débat en traçant un simple diagramme d’espace temps. Comme le disque est supposé infiniment fin, et que rien ne se produit dans la direction « z » nous pouvons supprimer le troisième dimension et traiter le problème en deux dimensions (spatiales), ce qui permet d’utiliser la dimension libérée pour représenter l’évolution temporelle.

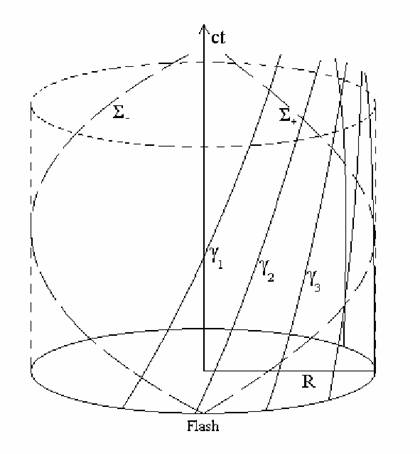
Comme montré sur la figure 3 ci dessus, {et non pas figure 4} (empruntée à [5]), les lignes d’univers les points de la périphérie du disque, dénotées , etc.. sont des hélices de type temps, comme de bien entendu, car des particules massives ne peuvent pas aller plus vite que la lumière. Les chemins et associés aux rayons lumineux issus d’un éclair lumineux et se propageant en sens contraire sont aussi des hélices, mais de type lumière comme il se doit, s’enroulant en sens contraire autour tu tube d’univers tracé par le disque. Ceci est en général admis et pas controversé dans la littérature.

Le problème se corse quand on essaie de définir le lieu des «  simultanéités » correspondant à la périphérie du disque. En utilisant la définition de la RR de la simultanéité, les évènements simultanés à un éclair vont être orthogonaux aux lignes d’univers de l’observateur en question (dans ce cas, un observateur chevauchant l’onde électromagnétique produite par l’éclair). L’intégration que nous avons faite au chapitre 5, est vue comme mesurant une courbe ouverte de type espace dans l’espace temps.

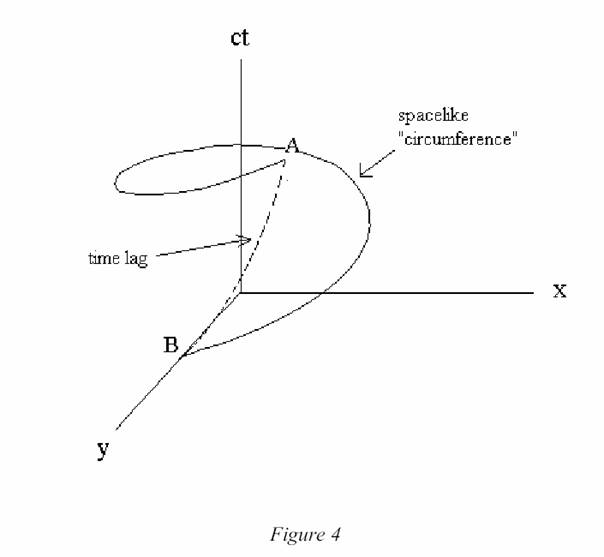
De la figure 4, il ressort que l’extrémité d’un ruban, appliqué sur la périphérie du disque ne va pas rejoindre l’autre extrémité au même point temporel. Les deux extrémités vont être séparées par une ligne d’univers de type temps dont la longueur est donnée par l’équation (5.2){ Homonomie de la boucle}. Quand , les lignes d’univers des points à la périphérie du disque, sont des droites et le lieu des évènements simultané à l’éclair est une courbe fermée de type espace.

Mais dès que le disque est mis en rotation, et devient une courbe ouverte, de sorte que la notion de simultanéité devient conventionnelle, dépendant du point de départ de l’intégration effectuée au chapitre 5. Remarquons aussi, qu’en combinant les figures 3 et 4, l’angle que les faisceaux lumineux et font avec les de type temps ( dans la figure 3) est égal à l’angle entre les rayons et la «circonférence» (dans la figure 4) : Ceci est évidemment dû au fait que la vitesse de la lumière mesurée dans les référentiels tangents inertiels est égale à « c ».

Alors que ceci est plutôt clair dans l’espace temps 4D , il est moins évident de dire ce que ceci signifie pour un observateur sur le disque.

Considérons un observateur muni, comme d’habitude, d’un nombre infini de minuscules petites règles et de deux horloges identiques synchronisées. Quand il voyage le long du bord du disque, à vitesse non relativiste ( par rapport au bord du disque), il dépose ses règles étalons et transporte une horloge avec lui. Lorsqu’il atteint de nouveau son point de départ, il va conclure que la circonférence correspond au nombre de règles étalons qu’il a déposé, soit :

.

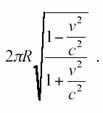Cependant, il va constater que son horloge retarde par rapport à celle qu’il a laissé sur place d’une valeur donnée par (5.2).

Nous voyons donc, que la courbure obtenue par la méthode suggérée par Moller est résulte du fait qu’on force artificiellement les points A et B dans la figure 4 à être réunis.

{On procède à une identification des points représentant les extrémités, comme cela se fait dans les espaces-temps « compacts ». Le disque en rotation est un espace temps compact. Il faut donc prendre en compte ce qu’on appelle « l’holonomie » de la boucle pour que cette indentification liée à la compacité de l’espace se fasse correctement.

Cette remarque s’applique évidemment à toute la classe de problèmes qui mettent en jeu des boucles dans l’espace-temps. Le paradoxe de Langevin par exemple, dans sa version classique possède cette caractéristique. L’holonomie est alors constaté par la différence de temps propre entre les jumeaux.

Formellement ceci peut être vu comme une conséquence du théorème de Stockes :dans une variété Riemannienne la circulation, d’une (n-1)_ forme linéaire M le long d’un contour fermé, délimitant une surface est égal à l’intégrale de surface «  flux » de la n_ forme dérivée dM . Cette intégrale est nulle seulement si la n-1 forme est exacte ou fermée }

7. Conclusion

Comme beaucoup de paradoxes, le paradoxe d’Ehrenfest naît de l’absence de notion de simultanéité absolue en Relativité. Il est clair que la plupart des physiciens qui ont étudié le disque en rotation, ont implicitement supposé que la circonférence du disque en rotation avait une géométrie bien définie. Cependant en s’appuyant sur des diagrammes de Minkowski, plutôt simples, on voit qu’une définition naturelle et cohérente de la simultanéité pour l’ensemble de la périphérie du disque n’est pas possible, ceci étant très caractérisé pour des rotations rapides. Si on décompose l’espace temps en temps et espace, les résultats de calculs ne vont pas permettre une vérification expérimentale ( en fait c’est ainsi que la courbure calculée au chapitre 4 apparaît)

Le plus simple est encore de voir les paradoxes du disque en rotation comme une déclinaison du paradoxe des jumeaux. C’est dans le changement incessant de référentiel de référence que le temps se « perd ».

Citons Rizzi et Tartaglia [5]

«  Un disque en rotation n’admet pas de « référentiel ( global) propre » bien défini. Il faut plutôt regarder cela comme une classe de référentiel constitué d’un nombre infini de référentiels locaux propres considérés aux différents points à différents instants et assemblés selon certaines règles »