FAQ | Tutorial : Part 1 | Part 2 | Part 3 | Part 4 | Age | Distances | Bibliography | Relativity
Original : Ned Wright Cosmology tutorial, part 4
Cours de Cosmologie par le professeur Edward .
L . Wright
www.astro.ucla.edu/~wright/cosmolog.htm
Cours Cosmologie première partie
Cours Cosmologie deuxième
partie
Cours Cosmologie troisième partie
Cours Cosmologie quatrième partie
Cours de Cosmologie : quatrième et dernière partie
Traduction libre: Jacques Fric qui endosse
toute la responsabilité des erreurs que sa traduction aurait pu introduire.
Commentaires personnels entre [..]
Retour vers la troisième partie
L'Inflation
Le scénario inflationniste développé par Starobinsky et par Guth, offre une solution au problèmes de longévité , de platitude et d'horizon de l'Univers [ la Totale]. Le scénario inflationniste ( inflationary scenario) fait appel à la densité d'énergie du vide (vacuum energy density). Habituellement nous pensons que le vide est "vide" et sans masse, et nous avons déterminé que sa densité est en tout état de cause inférieure 1E-30 gm/cc aujourd'hui. Mais en théorie quantique des champs, le vide n'est pas vraiment vide , mais plutôt rempli de particules virtuelles.
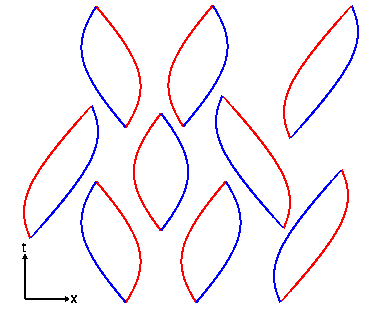
Le diagramme d'espace temps ci dessus montre la création Ex Nihilo
de paires particules-antiparticules virtuelles
s'annihilant tout aussi soudainement qu'elles se sont créées. Pour des
particules de masse m, on estime qu'il y a une particule virtuelle par volume
égal au cube de la longueur d'onde de Compton associée à cette particule, h/mc, où h est la constante de Planck [ vu la petitesse de
ce volume, cela en fait beaucoup]. Donc la densité supposée du vide
est rho = m4*c3/h3
ce qui est énorme. Pour la masse correspondant à la particule la plus lourde
que permet la théorie, la masse de
Planck M définie par 2*pi*G*M2 = h*c, cette densité est 2E91 gm/cc. Donc comme la densité d'énergie du vide est au moins de
121 ordres de grandeurs inférieure à l'estimation brute de la mécanique
quantique, il doit y avoir un mécanisme de "
compensation"manifestement très [ mais pas totalement ?] efficace. Si un petit résidu de
l'énergie du vide subsiste, cela se traduit par une constante Cosmologique . "cosmological constant"
qui est un mécanisme proposé pour être compatible avec les contraintes imposées
par le modèle avec Omegao=1 conduisant à
un âge de l'Univers de to = (2/3)/Ho = 10 Ga, et l'âge apparent des plus vieux amas globulaires,
16+/-4 Ga. L'énergie du vide génère une
"force"de répulsion de la matière ( antigravitation)
qui provoque l'accélération de l'expansion de l'Univers au lieu de son
ralentissement, et de ce fait accroît to pour un Ho
donné.
Le scénario inflationniste stipule que l'énergie du vide a été colossale pendant une brève période dans la prime jeunesse de l'Univers. Quand l'Univers est dominé par l'énergie du vide le facteur d'échelle croît exponentiellement, a(t) = exp(H(to-t)). La constante de Hubble reste alors constante pendant cette période, pas besoin de l'indice de référence d'époque. Si cette époque inflationniste dure suffisamment longtemps, la fonction exponentielle atteint une valeur considérable. Ceci rend a(t) très grand, et par conséquent le rayon de l'Univers très grand. Le diagramme ci dessous montre notre horizon (horizon) représenté sur une sphère de grand rayon en haut et sur une plus petite sphère en bas.Comme nous ne pouvons pas voir au delà de notre horizon, dans le cas inflationniste, sur cette sphère de grand rayon , l'univers nous paraît presque " plat" .
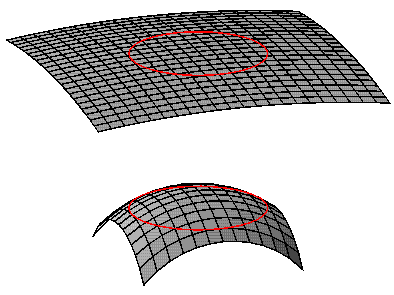
Ceci résout le problème de platitude et de longévité sous condition que cette
période d'expansion exponentielle dure au moins 100 fois plus longtemps que
l'âge de l'Univers quand elle a commencé. L'Inflation
résout aussi le problème de l'Horizon, car le cône de lumière du futur d'un
événement qui s'est produit avant l'inflation est énormément dilaté par le
processus d'inflation couvrant ainsi après l'inflation, une région très étendue
de l'Univers.
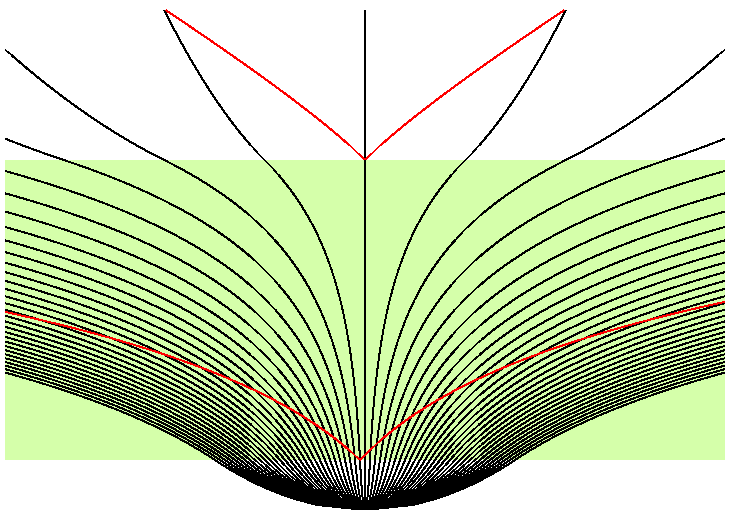
Ce diagramme d'espace temps montre l'époque inflationniste teintée en vert , et les cônes de lumière du futur issus de deux
évènements en rouge. L'événement avant l'inflation couvre une région très
importante qui peut recouvrir tout notre horizon, alors que l'autre plus tardif
est plus " normal". Ceci peut expliquer pourquoi la température du
RFC est si uniforme dans tout le ciel.
Détails: Structure à grande échelle et Anisotropie
Bien sûr l'Univers n'est pas parfaitement homogène et isotrope car il contient des régions denses comme les galaxies et les humains. Ces régions denses devraient modifier la température du RFC. Sachs et Wolfe (1967, ApJ, 147, 73) ont évalué l'effet des perturbations du potentiel gravitationnel sur le RFC. Le potentiel gravitationnel (gravitational potential,) phi = -GM/r, va être négatif dans des grumeaux denses et positif dans les régions moins denses. Les photons perdent de l'énergie pour émerger des puits de potentiel associés aux grumeaux.
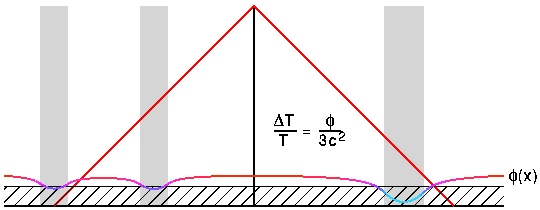
Le diagramme d'espace temps "conforme" ci dessus représente les
grumeaux par des barres verticales grises, l'époque avant le découplage
hachurée et le potentiel gravitationnel par une courbe codée par couleurs
phi(x). Quand notre cône de lumière du
passé coupe la surface de découplage nous voyons une température modulée telle
que dT/T = phi/(3*c2).
Sachs et Wolfe ont prédit des fluctuations dT/T
allant jusqu'à 1%, mais nous savons
maintenant que l'Univers est bien plus homogène que Sachs et Wolfe le pensaient. Donc les
observateurs travaillent depuis des années à améliorer la sensibilité pour
détecter ces petites fluctuations. La première anisotropie détectée fut
l'anisotropie dipolaire (dipole) par Conklin en 1969:
La représentation du RFC ci dessus est celle du satellite COBE et est
bien meilleure que celle qu'avait détecté Conklin. La
partie rouge est plus chaude d'un facteur (v/c)*To, tandis que la
partie bleue du ciel est plus froide du même facteur (v/c)*To, où la
vitesse évoquée est v = 370 km/sec. C'est ainsi que
nous mesurons la vitesse du système solaire par rapport à l'Univers observable.
Il s'est écoulé 23 ans avant que l'anisotropie prédite par Sachs et Wolfe soit
détectée par Smoot \etal
en 1992. L'amplitude était de 1 pour
100,000 au lieu de 1 pour 100:
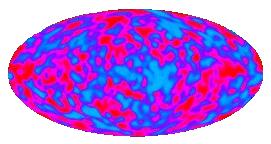
La carte ci dessus montre l'anisotropie cosmique ( et
le bruit du détecteur) après soustraction du motif dipolaire et du rayonnement
équatorial de la voie lactée. L'anisotropie de cette carte a un écart type 30 microK, et si cela est converti en potentiel gravitationnel
en utilisant les travaux de Sachs et Wolfe's et si on exprime ce potentiel par
une hauteur dans un champ gravitationnel
uniforme d'intensité égal au champ terrestre ( au
sol), nous obtenons une hauteur qui est égale à deux fois la distance Terre
- Soleil. Les montagnes et les vallées de l'Univers
sont plutôt grandes.
L'Inflation prédit une certaine distribution statistique de l'anisotropie. Les fluctuations quantiques n'affectent que des zones minuscules, mais l'expansion fantastique liée à l'inflation les a transformé en régions observables.

Le diagramme d'espace temps à gauche en haut montre les cônes de lumière du
futur des évènements liés aux fluctuations quantiques. Le haut de ce diagramme
est en fait un volume qui coupe notre cône de lumière du passé : le ciel
visible. Les cônes de lumière du futur des évènements deviennent des cercles
dans le ciel. Les évènements les plus anciens de l'époque inflationniste
tracent de larges cercles, comme montré sur la figure en bas à droite. Les
évènements ultérieurs tracent des cercles plus petits comme montré au milieu à
droite, mais il y en a plus donc la couverture du ciel est la même. Les événement encore ultérieurs tracent une multitude de
cercles encore plus petits offrant la même couverture du ciel, comme montré en
haut à droite.
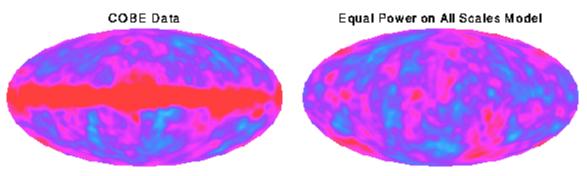
Le motif formé en additionnant tous les effets des évènements de tous les âges
est appelé " modèle à puissance indépendante d'échelle" et est
conforme aux observations de COBE .
Ayant constaté que le motif d'anisotropie est cohérent avec l'inflation, on peut se demander si son amplitude implique des forces gravitationnelles suffisantes pour produire la formation des amas de Galaxies observées..
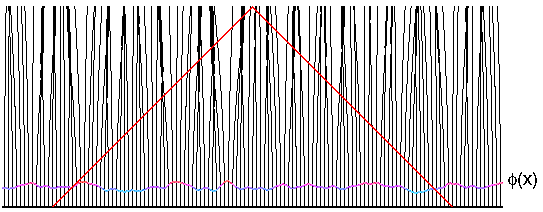
Le diagramme d'espace temps " conforme" ci dessus montre la fonction
phi(x) au découplage telle que mesurée par COBE, et les lignes d'Univers des
Galaxies qui sont perturbées par les forces gravitationnelles issues du
gradient du potentiel. La Matière s'écoule vers la vallée s'écartant des pics
de potentiel ( points rouges sur la carte COBE)
provoquant un vide dans la distribution actuelle des galaxies, alors que les
vallées de potentiel ( points bleus) sont les endroits d'accumulation où les
amas de galaxies (clusters)
se forment.
COBE ,du
fait ce sa faible résolution, ne fut pas capable discerner des domaines
suffisamment petits correspondant aux " germes " des amas ou même
super amas de galaxies, mais si nous utilisons la propriété "que le
spectre de puissance est indépendant d' échelle" pour extrapoler les
données de COBE à des échelles plus petites , nous trouvons que les forces
gravitationnelles sont suffisamment fortes pour produire les amas tels que nous
les voyons, mais sous réserve que ces forces ne soient pas opposées à
d'autres. Si la matière de l'univers
n'est composée que des éléments chimiques ordinaires, alors il y avait des
forces importantes qui s'opposaient avant le découplage, car les électrons
libres qui sont maintenant liés à des atomes se couplaient très facilement avec
les photons et étaient très efficaces pour
diffuser les photons du fond Cosmologique. Nous pouvons donc conclure
que l'essentiel de la matière dans l'univers est de la "matière
sombre" ("dark matter") qui n'émet
pas, n'absorbe pas, et ne diffuse pas la lumière ( photons).
Cette conclusion étrange devrait être confortée par une analyse plus fine de
l'anisotropie du RFC qui est une des missions de WMAP ( MAP
rebaptisé) (Microwave
Anisotropy Probe (MAP)) en 2000. [ WMAP a bien confirmé la
prédominance de matière et énergie sombre]
FAQ | Tutorial : Part 1 | Part 2 | Part 3 | Part 4 | Age | Distances | Bibliography | Relativity
© 1996-1998 Edward L. Wright. Last modified 7-Dec-1998