Commentaires de lecture sur : géométries, 1- Relativité restreinte

Ref : http://spoirier.lautre.net/intro.ps.gz, http://spoirier.lautre.net/physique.ps.gz

L'idée est que le même formalisme peut s'appliquer à des géométries différentes.

Nous sommes familiers avec la géométrie Euclidienne, où les notions de longueurs d'un segment, d'angle , de produit scalaire sont immédiates à notre imagination et peuvent être facilement représentées dans un système cartésien.

.

Ces notions ne sont que des cas particuliers de concepts existants ( liés la métrique en particulier) dans une variété de géométries.

Dans le cas de la Relativité restreinte, la géométrie associée à la métrique est "plate" , comme la métrique Euclidienne, c.a.d que ses coefficients ne dépendent pas des coordonnées ( métrique " hyperbolique" , Lorentzienne ou de Minkowski) , et correspond donc à un cas relativement simple, même si le ds² caractérisant sa métrique en coordonnées cartésiennes fait apparaître une signature diagonale (-c²,+1,+1,+1) ou l'inverse selon les conventions au lieu de (+v²,+1,+1,+1) pour la géométrie Euclidienne (en coordonnées d'espace).

A cette différence près les résultats de la géométrie Euclidienne écrits sous leur forme générale faisant intervenir la métrique peuvent se transposer ( vérifier que cela à un sens dans l'autre géométrie).

Pae exemple la norme d'un vecteur ( auto produit scalaire U²) , ou plus généralement le produit scalaire de deux vecteurs U et V fait intervenir la Métrique : U.V = U^m g_mn .V ⁿ

Avec les notations habituelles.

On peut aussi visualiser les échelles différentes des différentes coordonnées ( temps et espace) sur le diagramme représentatif du phénomène étudié pour plus de "conformité" du dessin au phénomène;

Entre la métrique de Minkowski et la métrique Euclidienne on voit que la seule différence est relative au coefficient du temps qui vaut -c², au lieu de +v² en coordonnées d'espace.

Pour l'homogénéïté, la coordonnée temps est affectée d'un coefficient v de Vitesse, on voit que comme les règles opératoires sont les mêmes entre les deux métriques, pour tout ce qui concerne les calculs de grandeur faisant intervenir la métrique, il suffira à la fin des calcul de remplacer v² par -c² et de rendre l'expression cohérente ( trigonométrie hyperbolique correspond à la trigonométrie classique sur des arguments imaginaire) pour obtenir rigoureusement le résultat.

Donc en résumé.

1- établir une correspondance ( rigoureuse) entre une description du problème dans un contexte intuitif ( problème de géométrie Euclidienne) et le problème à traiter dans son contexte théorique physique. Ceci se manifeste par une transformation

2- Résoudre le problème dans son contexte de géométrie Euclidienne où l'intuition est d'un grand secours

3- Utiliser la transformation établie plus haut pour obtenir le résultat dans le contexte physique.

Vérification de l'exemple p.9 ( courbe à accélération constante)

Application sur l'exemple du document cité en référence ( extrait ci dessous)

Diagramme représenté en espace Euclidien à deux dimensions ( plan)

B

Terre

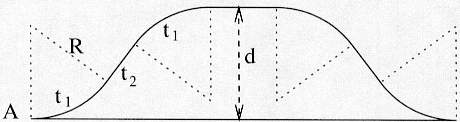
Pendant la durée de la poussée provoquant une accélération constante g, le véhicule parcourt un arc de cercle de longueur t₁,( temps "propre" du voyageur) en unité de temps ou vt_l en unité d'espace, d'angle a = t_1. g (ce qui donne en radians a.k = t_lg.v^-1, on rappelle que v ² = k^-2 ) et de rayon (en unité d'espace) R = v ². g^{- 1} .

Par des considérations simples sur la figure, on déduit:

d = 2R(l - cos(a.k)) + vt₂ sin(a.k) = 2v²g^-1(1 - cos(k.t₁g)) + t₂k^-1 sin(k.t₁g)

Transposé en espace de Minkowski par v ² = k^-2 = - c² , on obtient le résultat au problème de relativité :

d = 2c² g^-1 (ch(t_lg/c) - 1) + ct₂ sh(t_lg/c)

Même calcul pour la différence de longueur temporelle entre la courbe et la ligne droite

Dt = 4(t₁ - kR.sin(ka)) + 2t₂(l - cos(ka)) = 4(t₁ - c.g^-1 sh(t_lg/c)) + 2t₂(l -ch(t_l.g/c))

Ce qui est négatif, compte tenu que la ligne doite en espace de Minkowski est plus longue que la ligne courbe.

Calcul analytique de la partie courbe à partir des formules de Lorentz.

La similitude entre un opérateur décrit par de matrice de rotation en espace Euclidien (conservant le ds²) et l'opérateur matriciel associé au groupe de transformation de Lorentz (conservant également le ds² mais dans un espace de Minkowski dit hyperbolique) est en général soulignée. Il faut dire qu'elle saute aux yeux ( on remplace les fonctions trigonométriques par leurs équivalentes hyperboliques pour tenir compte de la signature de la métrique )

Si on part de la formule de Lorentz sous la forme matricielle et qu'on s'intéresse à x,t seulement, on a :

cdt' = cosh j.c.dt - sinh j.dx (1)

et dx' = - sinh j.cdt + cosh j.dx, (2)

Pour avoir le temps propre on pose x' =0, donc dx' =0, on applique dans (2) et on reporte le résultat dans (1), après un calcul élémentaire il vient:

dt/dt' = cosh j (3)

avec tanh j = v/c, donc en principe j = argtanh v/c. (4)

Ces formules sont valables pour deux référentiels quelconques animés d'une vitesse relative constante v selon l'axe des x,x' parallèles.

Elle s'applique dans notre cas ( accéléré) qu'à un instant infiniment court dt, dt' (autour du temps t, t') ou l'on suppose la vitesse relative est constante.

En fait on voit que t et t' sont la somme intégrale des dt et dt' correspondants aux différentes valeurs de j au cours du temps ( j varie puisque le système t' accélère, cf définition de j ) .

Reste à déterminer la variation de j fonction de t'.

Si on considère deux instants infiniments voisins du système en accélération t' et t'₊ =t' +dt', les formules (1) et (2) s'appliquent donnant le rapport entre dt' au temps t' et dt'₊ au temps t'₊ et que l'on examine la variation dj de j il vient de (4):

dj = argtanh dv/c avec dv = gdt'

soit en approximant argtanh gdt'/c au premier ordre par gdt'/c

dj = gdt'/c

j = gt'/c , la variation de l'angle est une fonction linéaire de t'

en reportant dans (3) on obtient:

dt/dt' = cosh gt'/c

En intégrant de t= 0 à t₁ et de j =0 à gt'₁/c, on a t₁ = t'₁ . c.g^-1( sinh g.t'₁/c) d'où on déduit Dt .

Pour la partie linéaire l'application de la formule (3) donne directement le résultat escompté.