Le principe de Mach et une théorie Relativiste de la Gravitation

Original : Mach's principle and a Relativistic Theory of Gravitation

C. Brans et R.H Dicke ( Physical review )1961

Palmer Physical Laboratory, Princetown University, Princetown; New Jersey

Traduction par J. Fric qui endosse toute responsabilité pour les erreurs que sa traduction aurait pu introduire, commentaires personnels entre [..]

Le rôle du principe de Mach en physique est discuté, en particulier sa compatibilité avec le principe d'équivalence. Les difficultés d'intégration du principe de Mach en Relativité générale sont discutés. Une théorie relativiste modifiée de la gravitation, apparemment compatible avec le principe de Mach est proposée.

Introduction.

Il est intéressant que seulement deux idées concernant la nature de l'espace aient dominé notre pensée depuis Descartes. Selon l'une d'elle l'espace est une structure absolue physique avec ses propriétés intrinsèques. On peut la suivre depuis Descartes , puis à travers Newton jusqu'à la théorie de l'éther du 19° siècle. La conception contraire est que les propriétés géométriques et inertielles de l'espace n'ont aucun sens dans un espace vide, car les propriétés physiques tirent leur origine de la matière qui y est contenue, et que le seul mouvement d'une particule qui ait un sens est celui par rapport à la matière de l'Univers. Cette conception ne s'est pas concrétisé parfaitement dans le cadre d'une théorie. Cette conception est également ancienne, on la trouve dans les écrits de Berkeley puis dans ceux de Mach. Ces idées ont trouvé une application limitée dans le cadre de la Relativité Générale, mais on doit reconnaître , que bien qu'en Relativité Générale la géométrie spatiale est affectée par la distribution des masses , elle n'est pas uniquement gouvernée par cette distribution. Il n'a pas été possible jusqu'à présent de spécifier des conditions aux limites dans les équations du champ en Relativité Générale qui mettrait la théorie en accord parfait avec le principe de Mach. Ces conditions devant entre autres éliminer toutes les solutions sans masses présentes.

Remarquons, que selon les idées de Mach , les forces inertielles que l'on observe localement dans un laboratoire accéléré peuvent être interprétées comme étant la conséquence de l'effet gravitationnel dû à la matière distante relativement accélérée par rapport au laboratoire. On peut montrer comment la Relativité générale ne satisfait qu'imparfaitement à ce principe sur l'exemple d'un laboratoire avec observateur unique flottant dans un espace vide. Si on utilise le référentiel de Minkowski attaché au laboratoire pour caractériser cette situation, en considérant le laboratoire de masse suffisamment petite pour que son influence sur la métrique soit minime, on peut considérer qu'on est dans l'approximation de "champ faible".

L'observateur peut conformément à la Relativité Générale, vérifier les lois habituelles de la physiques avec ses instruments. Cependant, toujours en vertu de la Relativité Générale, l'observateur peut générer un mouvement de rotation de son laboratoire en se penchant par une fenêtre et en tirant une balle avec son revolver tangentiellement. Par la suite, le gyroscope sensible de son laboratoire va continuer à pointer environ dans une direction pratiquement fixe par rapport à celle du projectile qui s' éloigne à alors grande vitesse. Le gyroscope va tourner relativement aux murs du laboratoire. Donc du point de vue de Mach, le projectile minuscule et de masse presque nulle et très éloigné semble jouer un rôle plus important que celui de la structure proche bien plus massive du laboratoire dans la détermination du référentiel inertiel et l'orientation du gyroscope ( Du fait de l'effet Lense Thirring le laboratoire " en rotation" va influer légèrement sur l'axe du gyroscope). Il est clair que ce qui est décrit ici est plus proche d'un espace absolu " à la Newton" qu'un espace physique au sens de Berkeley et Mach .

L''exemple ci dessus nous pose un problème. Apparemment nous devons supposer au moins une des possibilités suivantes:

1- L'espace physique a des propriétés géométriques et inertielles qui ne dépendent pas de la matière qui y est contenue.

2- L'exemple ci dessus est impossible en Relativité générale en raison de conditions aux limites que nous ne connaissons pas encore aujourd'hui.

3- La Relativité Générale ne permet pas de décrire correctement la situation physique ci- dessus.

Ces différentes possibilités ont déjà été discutées précédemment. Les objections à la première sont principalement d'ordre philosophique et comme indiqué précédemment nous renvoient vers Berkeley. La Relativité du mouvement, héritée d'Einstein, est maintenant largement considérée comme un acquis par la physique moderne. Comme l'Univers est non uniforme, il paraît difficile d'imposer des conditions aux limites qui auraient pour effet de proscrire les configurations de masses indésirables par rapport au laboratoire, où qu'il soit. Pourquoi le laboratoire ne pourrait il pas être à côté d'une étoile massive? Pourquoi cette étoile massive ne contribuerait elle pas à la réaction inertielle?

Cette difficulté est poussée à l'extrême, en considérant les lois de la physique , incluant ses aspects quantitatifs, à l'intérieur d'une coquille sphérique, statique et massive.

Il est bien connu que la solution de Schwarzschild à l'intérieur est plate et peut donc être exprimée dans un référentiel Minkowskien. En relativité Générale tous les systèmes Minkowskiens sont équivalents, donc la masse et le rayon de la coquille sphérique n'ont aucun effets discernables sur les lois de la physique à l'intérieur.

Apparemment, la coquille sphérique ne contribue en aucune manière aux effets inertiels en son intérieur. Qu'arrive t'il si la masse de la coquille décroît où si son rayon augmente indéfiniment? On peut remarquer que Komar ( Ph.D thesis, Princeton Universty 1956) a essayé sans succès de trouver des conditions aux limites et des conditions initiales convenables en Relativité Générale qui impliqueraient le principe de Mach.

La troisième possibilité est l'objet de cet article.

En fait, les objectifs de cet article sont en deçà d'une formulation d'une théorie, en complet accord avec le principe de Mach. Un tel programme comporte deux parties:

- établir une théorie qui conduit à des équations du champ

- formuler les conditions aux limites et conditions initiales convenables, qui ne font dépendre la géométrie de l'espace que de la distribution de matière.

La dernière partie n'est traitée que partiellement.

A la fin de l'article nous reviendrons rapidement sur le problème du laboratoire en rotation.

Un principe aussi radical que celui de Mach, de caractère essentiellement philosophique, en l'absence de théorie, ne peut être décrit que qualitativement.

Un modèle de théorie qui inclurait des éléments du principe de Mach a été décrit par Sciama (ref [7]) [ Monthly notices, Roy Astron. Soc. 113,34 (1953), The unity of the Universe].

En vertu d'arguments dimensionnels et de l'étude de Sciama, il apparaît que si on suppose valide le principe de Mach, la constante de Gravitation G est liée à la distribution de masse dans un Univers uniforme en expansion par :

Ou M est la masse de l'Univers observable ( en relation causale) et R le rayon de la limite de cet Univers observable [ horizon]. Les idées physiques sous tendues par (1) sont relatées dans les références [7] , [8] [ R.H Dicke, Am. Scientist 47,25 (1959)] et [9] [ R.H Dicke , Science 129,621 ( 1959)] et peuvent être résumées simplement. Comme stipulé avant, selon le principe de Mach, le seul mouvement significatif est celui par rapport au reste de la matière de l'Univers, et la réaction inertielle qu'on observe dans un laboratoire uniformément accéléré relativement à la matière distante de l'Univers peut être interprété comme une force gravitationnelle agissant sur un laboratoire fixe , due à la présence de matière distante accélérée [ 7]. Cette interprétation de la réaction inertielle a des implications intéressantes. Supposons un corps d'épreuve tombant vers le Soleil. Dans un système de coordonnées tel que le corps qui est attiré par le Soleil soit au repos, L'attraction du Soleil est compensé par une autre attraction gravitationnelle, la réaction inertielle. [8]. Remarquons que l'équilibre n'est pas rompu si on double toutes les forces gravitationnelles. Donc, l'accélération est déterminé par la distribution des masses dans l'Univers, mais est indépendant de l'intensité de ces interactions gravitationnelles. Si on désigne par ms la masse du Soleil, et par r sa distance, on peut exprimer l'accélération Newtonienne par a = G ms /r² , ou en vertu des arguments dimensionnels, en termes de distribution de masses par. Si on combine ces deux équations on retombe sur l'équation (1).

Cette relation ne s'applique seulement qu'au niveau des ordres de grandeur, mais elle suggère que, soit le rapport M/R est fixé par la théorie, soit la constante de gravitation observée localement est variable et dépendante de la distribution de masse par rapport à ce point. La première des hypothèses est, bien sûr, partiellement, la limitation de la distribution de masse qu'on peut espérer faire résulter de conditions aux limites sur les équations du champ de la Relativité Générale. La deuxième n'est pas compatible avec le principe d'équivalence " fort" et donc avec la Relativité Générale. Nous en discutons les raisons ci après.

Si la réaction inertielle peut être interprétée comme une force gravitationnelle due à la matière distante accélérée, il s'ensuit que les valeurs des masses inertielles des particules observées localement en point, vont dépendre de la distribution des masses par rapport à ce point. Notons cependant l' ambiguïté fondamentale d'une assertion de ce type, car nous n'avons pas de moyen direct de comparer la masse d'une particule comme un électron entre deux points différents de l'espace temps. Les rapports de masses peuvent être comparés en différents points, mais pas les masses. D'autre part la gravitation nous fournit une autre masse caractéristique.

et le rapport de masse , le nombre sans dimension.

nous offre une mesure non ambiguë de la masse d'un électron qui peut être comparée en différents points de l'espace temps.

On peut aussi remarquer que l'affirmation que h et c sont les mêmes en tous points de l'espace temps est aussi dénuée de sens, dans le même contexte tant qu'une méthode de mesure n'a pas été définie. En fait on peut noter qu'on peut poser h et c constants. Un ensemble de constantes physiques peut être posé comme "constant", s'ils ne peuvent pas être combinés pour former un ou plusieurs nombres sans dimensions. La nécessité de cette limitation est évidente, car un nombre sans dimensions est invariant par une transformation d'unité et la constance d'une grandeur physique sans dimensions ne peut être déterminée que par l'expérience. Un ensemble de "constantes" physiques indépendantes constantes par définition, est complet s'il est impossible d'en ajouter une autre sans générer de [ nouveaux] nombres sans dimensions.

Remarquons que si le nombre de l'équation (3) dépend de la position et si h et c sont constants par définition, alors soit m soit G ou les deux peuvent dépendre de la position. Il n'y a pas de différence fondamentale entre choisir m constant ou G constant. Cependant l'un peut mieux convenir que l'autre, car la structure formelle de la théorie, peut à première vue, être sensiblement différente selon le cas. Pour revenir à l'équation (3) la valeur inhabituelle [petite] de ce nombre sans dimension, a été souvent mise en exergue, ainsi que sa relation avec les grands nombres sans dimensions de l'astrophysique.

La relation apparente entre l'inverse du carré de ce nombre à l'âge de l'univers exprimé par un nombre sans dimension en termes d'unités de temps atomiques et la racine carrée de la masse de la partie observable de l'Univers exprimée en masses de protons a suggéré à Dirac une relation causale impliquant que la valeur de l'équation (3) dépende du temps. La signification de l'hypothèse de Dirac, par rapport au principe de Mach a été aussi discutée [ 8].

Dirac proposa un modèle Cosmologique à partir de ces coïncidences numériques. Ceci a été critiqué, car il va au delà de des données empiriques sur lequel il s'appuie [8]. Dans une autre de nos publications, ( R.H.D), nous montrons qu'elle donne des résultats qui ne sont pas conformes aux observations de la théorie moderne de l'évolution stellaire.

D'autre part, remarquons qu'une constante sans dimension aussi grande que l'inverse de celle de l'équation (3) est soit le fruit d'un caprice de la nature ou est en relation avec une autre constante très grande de la nature. En aucun cas il ne paraît naturel de construire une constante de la théorie de l'ordre de 10 ²³ à partir de facteur tels que 4 pi/3. Nous concluons donc, que bien que la structure détaillée de la Cosmologie de Dirac ne peut pas être justifiée par la preuve empirique plutôt mince sur laquelle elle est fondée, la conclusion plus générale concernant la variation dans le temps du nombre défini par (3) a une base beaucoup plus sérieuse. Si conformément à l'interprétation que nous avons faite du principe de Mach, le rapport des masses donné par (3) ne dépend que de la distribution de matière dans l'Univers, avec h et c constants par définition, soit la masse m soit la constante gravitationnelle G ou les deux doivent varier. Bien que ces deux alternatives décrivent la même situation physique, la forme de la théorie va dépendre largement du choix que l'on fera. Ainsi par exemple, on peut montrer facilement que des particules neutres et de spin zéro, dont les masses dépendraient de la position, ne se déplaceraient plus sur des géodésiques de la métrique. ( voir annexe 1)

Alors la définition du tenseur métrique serait différente dans les deux cas. Les deux tenseurs métriques seraient reliés par une transformation conforme.

L'arbitraire concernant le tenseur métrique qui résulte de l'infinité du choix des unités de mesure pose la question de la signification physique de la géométrie de Riemann en Relativité ( [12] E. P Wigner has questionned the physical significance of Riemannian geometry, 1961).

En particulier les 14 invariants qui caractérisent l'espace [ je suppose qu'il s'agit des 14 composantes du tenseur de Riemann qu'on ne peut pas annuler par des changement de coordonnées, cf Landau Lifschitz: théorie des champs ] ne sont généralement pas invariants sous une transformation conforme, interprétée comme une redéfinition du tenseur métrique dans le même espace ( [13] B. Hoffman Phys. Rev 89,49 , 1953).

Pire encore, une redéfinition plus générale des unités de mesure peut être utilisée pour annuler les 14 invariants. On peut dire que ces remarques ne doivent pas être interprétées comme jetant un doute sur la justesse et l'intérêt de la géométrie Riemanienne en Relativité , mais plutôt que telle ou telle géométrie n'est qu'une représentation bien particulière de la théorie. On escompte que le contenu physique de la théorie va être cohérent et "contenu" dans le groupe des invariants vis à vis des transformations d'unités et de coordonnées dépendant de la position.

Les invariants habituels de la géométrie Riemanienne ne sont pas invariants vis à vis de ce groupe plus vaste.

En Relativité Générale, les unités choisies dans la représentation garantissent que les propriétés physiques des atomes sont indépendantes de leur position. On suppose que ce choix est possible!

Conformément à cela, on fait un choix particulier d'unité, en sachant que ce choix arbitraire et sans signification d'invariance.

La structure théorique semble plus simple si on suppose les masses inertielles des particules élémentaires constantes, mais qu'on admet que la constante gravitationnelle puisse varier.

Remarquons que ceci est possible seulement si le rapport des masses des particules élémentaires est constant.

On peut raisonnablement en douter ( [10] R.H Dicke, Am.J.phys. 29,344 (1960)). Mais, comme d'autre part on peut supposer que des quantités comme le rapport des masses de particules ou la constante de structure fine, si elles dépendent des distributions de masses dans l'Univers, devraient y être moins sensibles que le nombre issu de l'équation (3) et cette variation pourrait être négligée dans un premier jus de la théorie. Remarquons également qu'exiger la constance du rapport entre les masses d'inertie gravitationnelle et purement gravitationnelles ajouté à la contrainte très forte d'isotropie spatiale impose des conditions si sévères qu'il s'est révélé difficile sinon impossible de construire une théorie satisfaisante avec une "constante" de structure fine variable.

Insistons sur le fait que l'argument ci dessus, qui se réfère à un grand nombre sans dimension, Eq(3) ne concerne pas le principe de Mach directement, mais le fait que principe de Mach associé à l'hypothèse d'une " constante " gravitationnelle qui dépend de la distribution des masses donnent une explication raisonnable à la possibilité de variation des "constantes".

On suppose que la matière proche et distante contribue à la réaction inertielle observée localement. Si la théorie était linéaire, ce qui est peu probable, Eq (1) suggèrerait que l'inverse de la constante gravitationnelle serait localement la superposition linéaire de toutes les contributions dues à la matière causalement connectée au point en question. Ceci pourrait être exprimé par quelque chose du genre.

Où la somme porte sur toute la matière qui peut contribuer à la réaction inertielle. On ne peut donner un sens exact à cette équation que dans le cadre d'une théorie à construire. L'équation (4) est aussi une relation de la théorie de Sciama.

Il est nécessaire de dire quelques mots sur le principe d'équivalence, tel qu'il est utilisé en Relativité générale et sa relation avec le principe de Mach. Tel qu'il est utilisé en Relativité Générale, le principe d'équivalence est plus que l'affirmation de l'équivalence d'un champ de gravitation et d'une accélération localement. En fait en Relativité Générale on suppose que toutes les lois de la physique, leur valeurs numériques inclues (telles que les constantes physiques sans dimension par exemple), telles qu'on les observe localement dans un laboratoire en chute libre, sont indépendantes du lieu et du temps ( du point d'espace temps où est situé le laboratoire). C'est l'expression du principe d'équivalence "fort". L'interprétation que nous avons donné ici du principe de Mach est évidemment incompatible avait ce principe d'équivalence "fort".

L'égalité locale (vérifiée à la précision des expériences actuelles) de l'accélération de toutes les masses dans un champ de gravitation est le principe d'équivalence "faible" [ connu depuis Galilée] . Remarquons que c'est le principe d'équivalence faible que l'expérience d'Eötvös a bien vérifié.

Avant de tenter de formuler une théorie de la Gravitation plus satisfaisante vis à vis du principe de Mach, que la Relativité Générale, résumons les hypothèses et les idées physiques que nous avons développées précédemment.

1- Une approche du principe de Mach qui, par des conditions aux limites, tente de n'autoriser que des distributions de masses qui produisent l'effet de réaction inertielle "correct" semble sans issue, du fait qu'il existe des masses importantes très localisées dans l'Univers (naines blanches, étoiles à neutrons, trous noirs ?) et qu'un laboratoire peut être en principe construit à proximité de telles masses. Il apparaît aussi possible de modifier la distribution de masse, par exemple une coquille massive sphérique en béton peut être construite avec le laboratoire à l'intérieur.

2- Le point de vue contraire est que les réactions inertielles locales observées dépendent de la distribution des masses dans l'Univers par rapport au point d'observation considéré et en conséquence toutes les valeurs quantitatives des variables des lois physiques observées (telles qu'on peut les retrouver dans les "constantes" physiques) vont dépendre de la position spatio-temporelle d'observation.

3 - Il est possible de ramener la variation de ces constantes physiques, nécessitées par cette interprétation du principe de Mach, à celle d'un seul paramètre, la "constante" gravitationnelle.

4- Le problème différent, mais cependant en relation, posé par l'existence de très grands nombres sans dimension, représentatifs d'aspects quantitatifs de des lois physiques, est clarifié par le fait que ces grands nombres sont en relation avec G et qu'ils sont du même ordre de grandeur que ceux qui caractérisent la taille et la distribution des masses dans l'univers.

5- Le principe d'équivalence "fort" , un des piliers de la Relativité Générale, est incompatible avec cette conception fondée sur le principe de Mach. Remarquons que les vérifications expérimentales très précises ( Eötvös) portent sur le principe d'équivalence faible.

Une Théorie de la gravitation basée sur un champ scalaire dans une géométrie Riemanienne

La théorie que nous allons développer représente une généralisation de la Relativité générale.

Ce n'est pas une théorie totalement géométrique de la gravitation , car les effets gravitationnels sont décrits par un champ scalaire dans une Variété Riemanienne.

Donc, les effets gravitationnels sont en partie géométriques et en partie dus à une interaction scalaire.

Il y a une relation formelle entre cette théorie et celle de Jordan, mais il y a des différences et l'interprétation physique est plutôt différente. Par exemple, l'aspect de création de masse de la théorie de Jordan, n'existe pas dans notre théorie.

Commençons le développement de notre théorie par le principe d'équivalence "faible". La grande précision de l'expérience d'Eötvös [ précision encore améliorée aujourd'hui ] , suggère que le mouvement, dans notre théorie, de particules de test non chargées, doit s'effectuer comme en Relativité Générale, sur des géodésiques de la Variété quadri dimensionnelle. En supposant que seule la "constante" de gravitation ( masses gravitationnelles actives ) dépend de la position, les lois de la physique ( à l'exclusion de la gravitation) observées dans un laboratoire en chute libre doivent être indépendantes du reste de l'Univers, sous réserve que les champs d'auto gravitation soient négligeables. La théorie doit prendre en compte cet effet.

Si la "constante" gravitationnelle doit varier, ce doit être selon une fonction d'un champ scalaire. La contraction du tenseur métrique est constante et donc dénuée d'intérêt dans ce contexte. Le scalaire de courbure [ scalaire de Ricci] et les autres scalaires formés à partir du tenseur de courbure sont également de peu d'intérêt car ils contiennent des gradients des composantes du tenseur métrique qui décroissent plus rapidement que r ^-1 à partir d'une source de masse. De tels scalaires tirent leurs contributions des masses proches plutôt que des masses distantes. Comme les scalaires de la Relativité Générale ne sont d'aucun secours, tournons nous vers de nouveaux champs scalaires. La fonction première d'un tel champ scalaire est la valorisation locale de la "constante" gravitationnelle.

De façon à généraliser la Relativité Générale, nous partons du principe variationnel utilisé en Relativité Générale, duquel sont déduit les équations du mouvement de la matière , les champs non gravitationnels et, bien sûr, l'équation d'Einstein du champ ( [18] Landau Lifschitz, théorie des champs), à savoir:

Où R est le scalaire de Ricci et L la densité de Lagrangien de tous les champs ( non gravitationnels) de matière.

Pour généraliser (5) nous commençons par la diviser par G , et une densité de Lagrangien d'un champ scalaire est ajoutée entre crochets. G est supposé être une fonction de Rappelons nous la discussion que nous avons eu au sujet de l'équation (4), il est raisonnable de supposer que G ^-1 varie comme , alors une équation d'onde simple pour , avec une densité scalaire de matière comme source, donnera une équation sensiblement de type identique à (4). La généralisation de l'équation (5) que nous cherchons est manifestement:

Ici joue un rôle analogue à G^-1 et a les dimensions ML^-3T². Le troisième terme est la densité de Lagrangien classique d'un champ scalaire, et le scalaire au dénominateur a été introduit pour faire de une constante sans dimension. Dans une théorie raisonnable doit être de l'ordre de grandeur des unités.

Remarquons que le terme de densité de Lagrangien relatif à la matière de l'équation (6) est le même à celui de l'équation (5). Donc les équations du mouvement de la matière dans un champ extérieur d'une métrique donnée sera le même qu'en Relativité Générale. La différence entre les deux équations réside dans les équations du champ gravitationnel qui déterminent gij , plutôt que dans l'équation du mouvement dans un champ associé à une métrique donnée. Il est donc évident que, comme en Relativité Générale le tenseur énergie impulsion de la matière doit être à divergence covariante nulle.

où

On suppose que L ne dépend pas explicitement des dérivées de gij .

La théorie de Jordan a été critiquée par Fierz [[19] Helv. Phys. Acta. 29,128 ( 1956) ], sur le fait que l'introduction de matière sur la théorie nécessite d'autres hypothèses concernant les standards de longueur et de temps. De plus, le création de masse et la non conservation du tenseur énergie impulsion posent sérieusement le problème de la signification du tenseur énergie impulsion chez Jordan. Pour montrer clairement que cette objection ne peut pas être soulevée dans notre théorie, insistons sur le fait que L est supposé être la densité de Lagrangien normale, fonction de la matière et de g_ij seulement, pas une fonction de .

Il est bien connu que pour une distribution raisonnable de champs métriques g_ij, ( une distribution qui n'est pas nécessairement solution des équations du champ de g_ij) , les équations du mouvement de la matière , obtenues en faisant varier les variables de matière dans l'équation (6) sont telles que l'équation (7) est satisfaite avec T ^ij défini par l'équation (8).

Alors l'équation (7) est satisfaite et notre théorie ne contient pas de principe de création de matière.

L'équation d'onde pour est obtenue de façon classique en en faisant varier et _,i dans l'équation (6). Ceci donne:

Ici le d'Alembertien covariant est défini comme la divergence covariante de ^,i

De l'équation (9) il est évident que .R et la densité de Lagrangien de sont les termes de sources pour la génération des ondes associées à . Chose remarquable, comme nous le montrerons plus loin, cette équation peut être transformée de sorte que le terme de source apparaisse comme le tenseur énergie impulsion contracté de la matière seulement. Alors conformément au principe de Mach, tire ses sources uniquement de la distribution de matière dans l'espace.

On obtient les équations du champ pour le champ métrique en faisant varier les composantes du tenseur métrique et de ses dérivées premières dans l'équation (6) ( principe variationnel).

Ceci est l'équivalent de l'équation d'Einstein du champ et est :

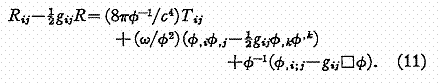
Le membre de gauche de l'équation (11) est familier et n'appelle pas de commentaire. Remarquons que le premier terme du membre de droite est la source habituelle de la Relativité Générale, mais avec le paramètre couplant la variable gravitationnelle ^-1. Remarquons que le second terme est le tenseur énergie impulsion du champ scalaire , aussi couplé avec la variable gravitationnelle ^-1. Le troisième terme est étranger et résulte de la présence des dérivées secondes du tenseur métrique dans R dans l'équation (6). Ces dérivées secondes sont éliminées par intégration par parties et produisent une divergence et les termes supplémentaires. Remarquons que quand le premier terme du membre de droite de l'équation (11) est prépondérant, cette équation ne diffère de celle d'Einstein que par la présence d'une "constante" gravitationnelle variable.

Alors qu'à première vue les termes "supplémentaires" de l'équation (11) peuvent paraître bizarres, leur rôle est essentiel. Ils sont nécessaires si on veut que l'équation (7) soit cohérente avec les équations (9) et (11). On peut voir cela en multipliant Eq (11) par f et en prenant la divergence covariante de l'équation qui en résulte. La divergence de ces deux termes annule le terme _,i .R_jⁱ = _,i .R_ji. Pour montrer ceci on utilise la propriété bien connue du Tenseur complet de courbure qu'il est le commutateur de deux dérivations covariantes successives sur un même vecteur arbitraire [ il me semble qu'on obtient ainsi le tenseur de Riemann plus le tenseur de torsion, il faut supposer la torsion nulle]. Si l'équation (11) est contractée ceci donne:

-

L'équation (12) peut être combinée avec l'équation (9) pour donner une nouvelle équation d'onde pour ( cf différences avec la théorie de Jordan dans la note (20) de l'original)

Avec la convention de signe

Pour un fluide

Tel que

Où est la densité de la matière dans les coordonnées co-mobiles et p la pression du fluide. Avec cette convention de signe et positif, la contribution à d'une masse locale est positive. Remarquons cependant qu'il n'y a pas de contribution électromagnétique directe à T , car la contraction du tenseur énergie impulsion d'un champ électromagnétique est identiquement nulle. Cependant , l'énergie électromagnétique liée contribue indirectement à travers les termes de contraintes ( stress) dans d'autres champs, la contrainte (stress) étant nécessaire pour confiner les champs. En conclusion , doit être positif si on veut que la contribution de la matière environnante à la réaction inertielle soit positive.

L'approximation champ faible

Nous allons calculer maintenant une solution approchée aux équations (11) et (13). La solution champ faible a la même importance qu'en Relativité Générale. Comme en Relativité générale, nous écrivons le tenseur métrique :

où est le tenseur métrique Minkowskien

h_ij est calculé à l'approximation du premier ordre seulement.

De façon similaire posons

Où ₀ est une constante et est calculé au premier ordre en densité de masses.

La solution champ faible de l'équation (13) est calculée en premier. Dans cette équation g_ij peut être remplacé par

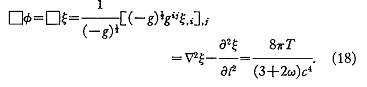
Il est évident qu'une solution temps retardé à l'équation (18) peut s'écrire

Où T doit être calculé au temps retardé considéré.

La solution dans l'approximation champ faible à l'équation (11) est obtenue de la même manière qu'en Relativité Générale en introduisant une condition de coordonnées qui simplifie l'équation.

Commençons par

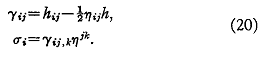
L'équation (11) peut être écrite au premier ordre en h _ij et :

L'équation (21) se simplifie en introduisant les quatre conditions de coordonnées

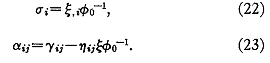
L'équation (21) devient alors

avec la solution temps retardée

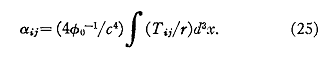
des équations (20) et (23)

Donc

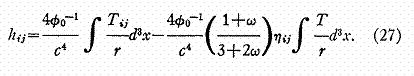
Pour une masse ponctuelle statique M ces équations deviennent

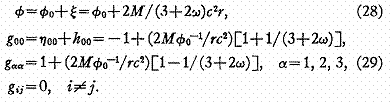
Les solutions champ faible ci dessus sont suffisamment précises pour discuter du décalage gravitation vers le rouge et de la déviation de la lumière.

Cependant pour discuter de l'avance du périhélie de l'orbite de Mercure, il nous faut une solution précise au deuxième ordre sur g₀₀.

Le décalage gravitationnel vers le rouge est déterminé par g₀₀, qui détermine aussi le poids gravitationnel des corps. Donc nous ne trouverons aucune anomalie dans ce redshift. Le facteur bizarre ( 4 + 2 ) ( 3 + 2 ) qu'on trouve dans g₀₀ est simplement celui intégré dans la définition de la constante gravitationnelle

D'autre part , il y a une anomalie dans la déviation de la lumière. Elle ne dépend pas que de g₀₀ seul, mais du rapport . On peut facilement calculer que la déviation de la lumière prédite par cette théorie diffère de celle de la Relativité générale par ce rapport.

Donc la déviation de la lumière calculée à partir de notre théorie vaut:

Où R est la distance minimum du rayon lumineux au Soleil de masse M. La différence avec la Relativité Générale est représentée par la valeur entre crochet. La précision des mesures sur cette déviation est trop médiocre pour en tirer quelque conclusion que ce soit sur la valeur limite de . Tout au contraire , nous avons une bonne précision dans l'avance du périhélie de l'orbite de Mercure et cela peut nous servir à déterminer une limite à .

Pour pouvoir discuter de ce point, nous devons établir la solution exacte du système autour d'une masse ponctuelle statique.

Champ statique à symétrie sphérique autour d'une masse ponctuelle

La forme de l'intervalle différentiel d'espace temps d'un espace isotrope est:

où et sont des fonctions de r seulement. Pour > 3/2 , la solution générale dans le vide est de la forme:

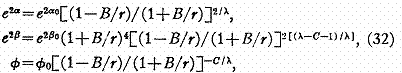
où

et ₀, ₀, ₀, et C sont des constantes arbitraires. On peut voir en insérant les équations (31) et (32) dans les équations (13) et (11) que c'est la solution statique à symétrie sphérique quand T_ij = 0 [ dans le vide].

Pour discuter de la rotation du périhélie de l'orbite d'une planète autour du Soleil, nous devons définir les constantes arbitraires de l'équation (32), de sorte d'assurer la cohérence de l'équation avec la solution limite champ faible [ au premier ordre en M / f_0.rc² ] donnée par les équations (28) et (29) obtenues précédemment. On peut vérifier que cela conduit au choix des constantes suivant:

0 donné par l'équation (29a)

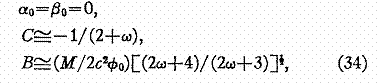
Avec donné par l'équation (33)

Rappelons nous notre discussion précédente du principe de Mach, il est clair que le caractère asymptotiquement Minkowskien de la solution n'a de sens que s'il y a de la matière à grande distance. Deuxièmement, la solution champ faible n'est valide que si le Soleil possède une distribution de masses qui y correspond. En clair, le champ généré par le Soleil doit être faible partout , y compris à l'intérieur. Avec ces hypothèses, la solution donnée par les équations (31), (32), (33), et (34) est valide pour le Soleil. Pour autant, ceci ne justifie pas leur utilisation, pour une masse ponctuelle.

On peut se demander si la solution, précise au première ordre en M / _0.rc² , est encore applicable et valide au deuxième. Remarquons cependant que cela nous a permis d'assigner des valeurs précises aux paramètres ajustables de l'équation (32), à l'exception de B dont nous ne demandons pas que la valeur résulte de l'intégration de la distribution de matière du Soleil, mais soit déterminée par la période des orbites des planètes.

Avec la solution ci dessus, c'est un jeu d'enfant de calculer la rotation du périhélie. Le calcul se simplifie si on se limite au deuxième ordre pour e² en M / _0.rc² et au premier ordre pour e². Cela donne:

Ce résultat est intéressant car il permet de fixer des valeurs limites pratiques à la constante w.

On admet que les résultats des observations sont en accord à mieux que 8 % avec ce que prédit la Relativité Générale. Il est donc nécessaire que dans l'équation (35) satisfasse à l'inégalité:

Le résultat des observations concernant le rotation résiduelle du périhélie de Mercure ( après soustractions des effets connus non relativistes ) est de 42,6 " ± 0,9 " par siècle.

Pour w = 6 notre théorie prédit 39,4 ". La différence de 3,3 " par siècle est 3,3 fois l'erreur formelle probable.

Des travaux récents ( Relatés par le Dr Clemence) sur les masses de Vénus et du système Terre Lune augmentent encore l'écart à 3,7" en réduisant l'erreur formelle par un facteur 2.

Bien que l'erreur formelle probable soit substantiellement plus petite que 3,2" d'arc , on peut raisonnablement l'élargir compte tenu des erreurs systématiques dans les observations, et sur le fait qu'en mécanique céleste nous avons de nombreux exemples, de marges d'erreurs qui se sont révélées complètement obsolètes du fait de nouvelles observations

Suivent quelques exemples sur la mesure de l'inverse de masse de Saturne, exprimé en inverse de Masse du Soleil

M^-1 = 3501,6 ± 0,8, Bessel (1883) déduit du mouvement de Titan satellite de Saturne

3494,8 ± 0,3 Jeffrey (1954) et G. Struve ( 1924-37) (Titan)

3502,2 ± 0,53, Hill (1895) Perturbation de Jupiter par Saturne

3497,64 ± 0,27 Hertz (1953) Perturbation de Jupiter par Saturne

3499,7 ± 0,4 Clemence (1960) Perturbation de Jupiter par Saturne

Cet exemple peut être atypique, mais il suggère qu'il faut être prudent en matière de marge d'erreur en mécanique céleste. [ pour Mercure, compte tenu qu'on observe un déplacement géométrique, à priori cela ne devrait pas trop s'appliquer ]

Principe de Mach

Une analyse exhaustive de la conformité de notre théorie avec le principe de Mach ne sera pas entreprise ici. Cependant du fait que cette théorie est motivée par le principe de Mach, il est souhaitable d'en discuter brièvement, même incomplètement. Nous avons établi les équations du champ, mais il reste à fixer les conditions initiales et aux limites pour être conforme au principe de Mach. Nous ne le ferons pas de façon générale , mais dans le cadre de certains problèmes seulement.

La discussion qualitative dans l'introduction suggérait que pour une coquille statique de rayon R et de masse M, la constante gravitationnelle , à l'intérieur devrait satisfaire la relation.

Soit de façon équivalente

remarquons que dans un espace plat , avec la condition aux limites = 0 à l'infini, l'équation (13) a une solution pour l'intérieur r < R

C'est un signe encourageant, et cela plaide bien en faveur du principe de Mach dans la théorie. Ne nous laissons pas abuser pour autant, par ce résultat simple. Il y a plusieurs raisons d'invalider quantitativement l'équation (39).

D'abord l'espace n'est pas plat, mais déformé en présence de la coquille massive.

Ensuite , la condition au limites qui fait tendre asymptotiquement vers 0 peut se révéler impossible pour une solution exacte statique à l'équation du champ.

Enfin, il peut se révéler impossible de construire une telle coquille massive, dans un Univers vide exception faite de la coquille, sauf à donner à la matière des propriétés non physiques.

Ce dernier point , n'invoque pas de limitation pratique aux matériaux réels, mais plutôt une limite fondamentale du tenseur énergie impulsion de la matière. Dans le même ordre d'idées, on peut remarquer que si l'équation (37) doit être satisfaite, indépendamment de la taille et de la masse de la coquille, les contraintes gravitationnelles induites sont énormes, de l'ordre de grandeur de la densité d'énergie de la coquille sphérique. Il n'est pas possible de réduire la contrainte en diminuant M ou en augmentant R, car la variation de la constante gravitationnelle qui en résulte compense cette modification. Nous ignorerons pour le moment ce troisième point et supposerons qu'une telle coquille peut en principe être construite.

Intéressons nous à la coquille massive, et considérons d'abord les solutions des équations du champ dans la région extérieure r > R. Cette solution relève de la solution générale régie par les équations (32) et (33). Notons que la condition aux limites :

n'est pas possible.

D'un autre côté, il est possible de changer le signe dans les crochets de l'équation (32) et intégrer le facteur complexe dans la constante devant les crochets. Ces équations peuvent alors être supposées s'appliquer pour r < B plutôt que pour r > B comme dans l'équation (32). Ces équations ont maintenant la forme

On peut remarquer que cette solution, intéressante pour r > R et seulement, conduit à un espace fermé de rayon r = B si

De même au rayon en question, ® 0 si C > 0

Les équations (36) et (33) exigent que

On peut voir que cette condition aux limites est en accord avec le principe de Mach sur une application du théorème de Green.

Introduisons une fonction de Green , satisfaisant

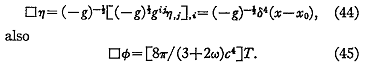
et aussi

ƒ f = [ 8p / ( 3 + 2w ) c⁴ ] T (45)

En combinant les équations (44) et (45) après les multiplications appropriées on trouve

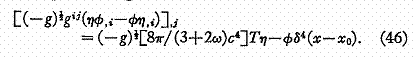
On suppose que est une solution " ondes avancées" de l'équation (44), c.a.d = 0 pour un temps postérieur à t₀. L'équation (42) impose que la lumière se propage du rayon B au rayon R , le rayon de la coquille, en un temps fini ( exprimé dans ce système de coordonnées), et de là, jusqu'à un point intérieur x₀ quelconque. Intégrons l'équation (46) sur l'intérieur de l'espace fermé ( r < B ) entre les temps t₂ > t₀ et l'espace de type surface S₁ , choisi de sorte que la fonction d'onde h démarre au rayon r = B au temps associé à cette surface et telle que la normale à cette surface à r = B n'a pas de composante dans la direction r. L'intégrale du membre de gauche de l'équation (46), après conversion en intégrale de surface , s'annule pour et ₀ les deux s'annulant à t₂, et à la fois et _i s'annulent sur S₁ à r = B avec i ¹ 1.

L'intégrale du membre de droite de l'équation (46) donne:

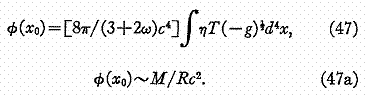
Remarquons que cette équation établit qu'en un point x₀, est déterminé par une intégrale sur la distribution des masses , avec une contribution par chaque élément de masse représentée par une ondelette qui se propage jusqu'au point x₀. Ceci est bien l'interprétation que le principe de Mach nous suggère.

Cosmologie

Un problème physique encore plus intéressant à discuter vis à vis du principe de Mach est le modèle cosmologique dérivé de cette théorie.

Rappelons que le principe Cosmologique a été bien vérifié par la fuite de Galaxies, à grande échelle. La cinématique du système de coordonnées co-mobiles est complètement libre de considération dynamique. L'intervalle d'espace temps élémentaire en coordonnées sphériques, s'écrit:

avec = + 1 pour un espace fermé, = - 1 pour ouvert et = 0 pour un espace plat, et où r <1 pour un espace fermé.

L'âge de Hubble associé au taux d'expansion de l'Univers et le décalage vers le rouge sont a/a' = a/(da/dt)

La substitution

simplifie l'expression de intervalle d'espace temps élémentaire en:

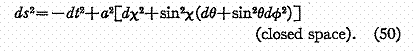
Le cas physique le plus intéressant est celui de l'espace fermé.

Ecrivons la composante (0,0) de l'équation (11) en utilisant la métrique définie par l'équation (50)

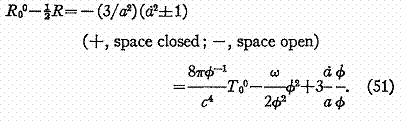
En supposant la pression négligeable dans l'univers nous avons - où la densité de masse est ( les observations indiquent

En supposant toujours la pression négligeable , le produit de la densité d'énergie par unité de co-volume est constant. Soit:

n reportant ceci dans l'équation (51) cela donne

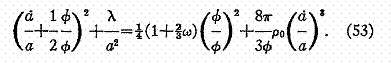
Ici ₀ et a₀ sont les valeurs de ces variables au temps t₀. De même l'équation (13) devient

En intégrant l'équation (54) on obtient:

La constante d'intégration t_c dans l'équation (55) peut être déterminée en considérant le principe de Mach.

Comme précédemment, nous avons introduit le principe de Mach dans ce problème en exprimant (t) comme une intégrale d'onde avancée de toute la matière. Les équations (46) et (47) nécessitent quelques hypothèses sur l'histoire de la matière dans l'Univers. Nous supposons que l'Univers s'est étendu à partir un état très condensé. Il est possible que dans le champ gravitationnel très intense de cet état très condensé de la matière soit créée. Pour un Univers fermé, de la matière provenant d'un cycle antérieur peut ainsi être régénérée dans cet état à très haute température.

Compte tenu de notre ignorance sur ce point, ce serait spéculatif d'en discuter les modalités. En tout état de cause, la création de matière n'est pas traitée par cette théorie.

Supposons alors un état initial, au début de l'expansion ( t = 0) avec et de la matière déjà présente. Bien que la pression à ce stade a du être très grande dans un état aussi condensé, avec l'expansion, elle va rapidement décroître et le fait de la négliger ne va pas mettre en péril le modèle.

En fait si on effectue une intégration de la phase haute pression initiale, pour un modèle Cosmologique donné, on voit que négliger cette phase de pression n'apporte pas d'erreur significative.

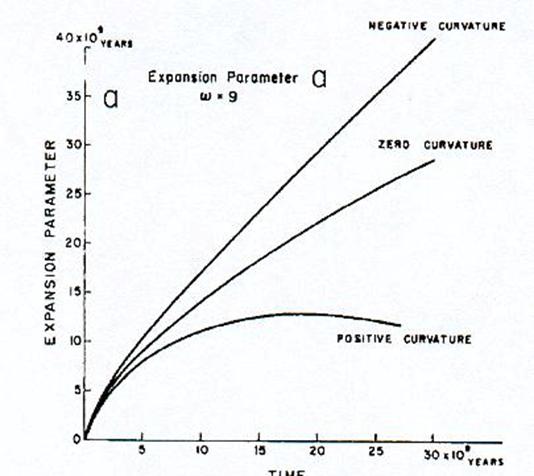
Figure 1 : Le paramètre d'expansion a fonction pour les trois cas d'espace, fermé, ouvert et plat pour w = 9

On suppose que la réaction inertielle, et donc , au temps t₀ est déterminé uniquement par la distribution de matière de t = 0 à t = t₀ . Donc, si l'équation (46) est intégrée sur l'espace 3D de t = 0 à t = t₁ > t₀ , l'intégrale de surface résultant du membre de gauche doit s'annuler. Les conditions initiales pour les équations (53) et (55), c.a.d les valeurs de a et de à t = 0 et la valeur de la constante t_c doivent donc être choisies de façon à annuler l'intégrale de surface de l'équation (46). Pour que cette intégrale de surface soit définie à t = 0, a doit être un infinitésimal positif , sur la surface , sinon le tenseur métrique est singulier. Si t_c = 0 et

= 0 sur cette surface , l'intégrale de surface s'annule. Ceci est la conséquence de l'annulation des facteurs et a³_,0 [ voir équation (55)] qui se produisent dans l'intégrale. On en conclut qu'il faut prendre a = = 0 avec t_c = 0, comme conditions initiales.

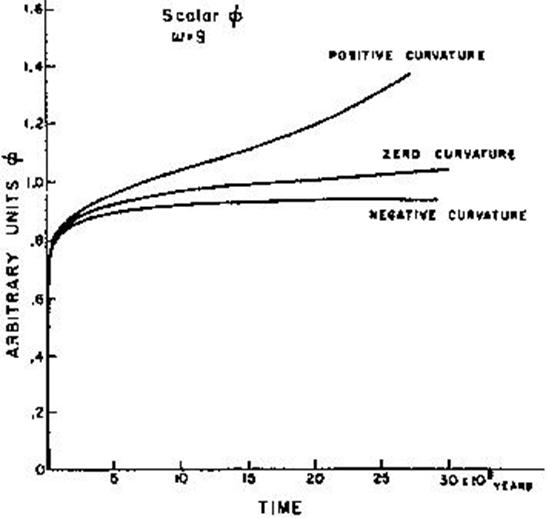
Figure 2: Le scalaire f, en unité arbitraire, fonction de t pour les trois cas d'espace fermé, ouvert et plat avec w = 9.

Remarquons que l'autre intégrale de surface , sur la surface t = t₁ s'annule car et tous ses gradients sont nuls sur cette surface ( solution, ondes avancées).

Avec t_c = 0 dans l'équation (55) et en combinant avec l'équation (53) on obtient:

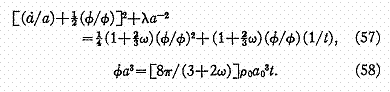On peut voir que pour un temps suffisamment petit le terme 1/a² dans l'équation (57) est négligeable et que le solution ne diffère de celle d'un espace plat que d'un facteur infinitésimal. Les équations résultantes peuvent être intégrées exactement avec les conditions initiales:

Comme les deux équations (57) et (58) sont maintenant (dans cette approximation) homogènes en (a, a₀), la solution est déterminée dans un facteur d'échelle en a seulement.

Cette solution, adaptée à la phase d'expansion primordiale ( a >> t) s'écrit:

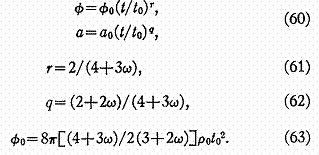
Pour un espace plat, la solution est exacte to tout t > 0.

Remarquons que l'équation (63) est compatible avec l'équation (1), car dans l'équation (1) M est de l'ordre de grandeur de et R est approximativement ct₀. Donc les conditions initiales prises sont bien compatibles avec le principe de Mach, tel que nous l'avons formulé ici.

Pour un espace courbe la seule méthode possible pour intégrer les équations (57) et (58) , au delà de la plage de validité de la solution ci dessus est une intégration par calcul numérique.

Un exemple de ces intégrations est donné figures 1 et 2 , où a et sont tracés en fonction du temps, pour les trois cas d'espace, fermé, ouvert et plat avec = 9.

Remarquons que pour ³ 6 et pour la solution d'espace plat, la variation de a en fonction du temps ne diffère que de peu du cas correspondant en Relativité Générale ( Einstein- De Sitter) où a t^2/3. En conséquence il va être difficile de discriminer les deux théories par étude de la géométrie de l'espace seulement. De même la densité de masse correspondant à un âge de Hubble particulier a/a' ( espace plat) est la même qu'en Relativité Générale si >> 1 . Pour = 6 , il n'y a que 2% de différence entre les deux théories.

D'autre part, le taux d'évolution stellaire est une fonction sensible à la constante gravitationnelle, et cela offre un possible test de la théorie. Ce point est discuté dans un autre article par l'un de nous ( R.H.D)

Au début de cet article , nous avons posé un problème, pour comprendre, dans le cadre du principe de Mach, les lois de la physique dans un laboratoire mis en rotation dans un Univers pratiquement vide. Nous sommes en mesure de comprendre, maintenant ce problème. Considérons le Laboratoire idéalisé par une coquille sphérique de masse m et de rayon r, et stationnaire dans le système de coordonnées co-mobiles donné par l'équation (50) avec les équations (60), (61), (62) satisfaites. Imaginons que le laboratoire est mis en rotation autour d'un axe avec une vitesse angulaire . Cette rotation affecte le tenseur métrique à l'intérieur de la coquille sphérique, de sorte qu'il va provoquer une précession du gyroscope avec une vitesse angulaire:

Où ₀ est donné par l'équation (63). L'équation (64) est valide dans l'approximation champ faible seulement si m /3 rc²₀ << 1. En substituant équation (63) dans (64) on obtient:

Remarquons que si la densité de matière de l'univers décroît, à t₀ constant , s'accroît. Alors, quand l'Univers se vide, la précession Lense Thirring du gyroscope s'approche de plus en plus de la rotation du laboratoire. Malheureusement, l'approximation, champ faible ne permet pas l'étude du cas limite quand ® 0.

Dans une autre publication, l'un de nous ( C.B) , d'autres aspects de la théorie, incluant les lois de conservation seront discutées.

Remerciements

Les auteurs remercient C. Misner pour son apport à travers les conversations que nous avons eues et les conseils qu'il nous a donné. Nous remercions P.Roll et D. Curott pour l'intégration numérique des solutions cosmologiques [ Eqs (49) et (50)] dont une partie est représentée sur les figures 1 et 2.

Annexe

En Relativité générale le mouvement d'une particule ponctuelle, sans spin, se déplaçant dans un champ gravitationnel seulement est obtenue par application du principe variationnel.

ou

Si la masse dans l'équation (66) est supposée être fonction de la position

Un terme de force supplémentaire apparaît et:

Les deux équations sont cohérentes avec la contrainte uⁱu_i = 1.

Remarquons que du fait du terme relatif à la force additionnelle dans l'équation (69), le particule ne se déplace plus sur une géodésique de la géométrie.

Si maintenant nous redéfinissons la géométrie de sorte que le nouveau tenseur métrique soit (transformation conforme)

et

L’équation (69) peut être écrite

La particule se déplace sur une géodésique de la nouvelle géométrie. Avec de nouvelles unités de longueur, de temps, et de masse appropriés à cette nouvelle géométrie, la masse de la particule est m₀, une constante.