Relativité Générale: Commission
Cosmologie de la Société Astronomique de France, Avril 2002
Présentation de la théorie de la Relativité Générale.............................................................................................................................................................. 4
0- Préambule........................................................................................................................................................................................................................... 4
1-Introduction........................................................................................................................................................................................................................ 4
2-L'application à la Cosmologie........................................................................................................................................................................................... 4
3-Recette pour une théorie de la Relativité Générale....................................................................................................................................................... 4
4-Les fondements de la RG.................................................................................................................................................................................................. 4
5-Les Idées Nouvelles.......................................................................................................................................................................................................... 4
6-La mise en œuvre................................................................................................................................................................................................................ 4
7-Géométrie de la relativité Générale, des concepts difficiles à se représenter............................................................................................................ 4
8-Les outils, tenseurs, Calcul tensoriel.............................................................................................................................................................................. 4
9-Les résultats........................................................................................................................................................................................................................ 4
10- L'élaboration laborieuse de la théorie.......................................................................................................................................................................... 4
11- L'approximation Newtonienne....................................................................................................................................................................................... 4
12- De la réalité physique des coordonnées en Relativité générale.............................................................................................................................. 4
13- Conclusion...................................................................................................................................................................................................................... 4
14- Références Bibliographiques........................................................................................................................................................................................ 4
14- Glossaire........................................................................................................................................................................................................................... 4
0 - Préambule.............................................................................................................................................................................................................................. 5
1- Introduction........................................................................................................................................................................................................................... 7
Cette assertion brutale présente quelques petites subtilités qui méritent d'être explicitées...................................................................................... 7
- Théorie de la gravitation ( ne concerne pas les autres interactions).......................................................................................................................... 8
- La gravitation n'est pas une force ( FAQ 1) (Rappel Relativité Restreinte )............................................................................................................ 9
Gravitation : Son extrême faiblesse................................................................................................................................................................................... 10
Gravitation : Son universalité............................................................................................................................................................................................ 10
Lumière.................................................................................................................................................................................................................................. 10
Espaces non Euclidiens...................................................................................................................................................................................................... 11
Equations Covariantes....................................................................................................................................................................................................... 11
Enfin la cerise ( sur le gâteau) : Métrique variable en fonction du temps ( FAQ2)................................................................................................... 12
Ce qu'en dit Einstein (ref 2)................................................................................................................................................................................................ 17
Limpidité de la démarche : Deux principes seulement pour une équation.................................................................................................................. 18
Homogénéité et Cohérence................................................................................................................................................................................................ 19
Succès et fécondité............................................................................................................................................................................................................. 21
2- L'application à la Cosmologie............................................................................................................................................................................................ 22
Einstein équation originale Poisson ( Newton)..................................................................................................................................................... 22
Einstein équation modifiée................................................................................................................................................................................................. 22
Quelques définitions ( provisoires):................................................................................................................................................................................. 22
Qu'est ce qu'un tenseur ?................................................................................................................................................................................................... 22
Comment modéliser la répartition de l'énergie au niveau de l'Univers ?..................................................................................................................... 23
Qu'est ce qu'une métrique ?............................................................................................................................................................................................... 24
Comment déduire de l'équation tensorielle de la gravitation des équations classiques.......................................................................................... 25
Quelques modèles très simples......................................................................................................................................................................................... 26
Modèle statique d'Einstein................................................................................................................................................................................................ 27
2- Modèle de De Sitter ( Univers vide)............................................................................................................................................................................. 30
Annexe 1 :Méthode de calcul pour modèle De sitter.................................................................................................................................................... 31
3-Recette pour une théorie de la relativité générale........................................................................................................................................................... 33
Disposer d'une théorie de Relativité restreinte comme modèle à généraliser............................................................................................................. 33
Idées de généralisation du principe de relativité............................................................................................................................................................ 33
Principe d'équivalence........................................................................................................................................................................................................ 33
Outils pour opérer des changements de coordonnées très généraux ( Calcul tensoriel)......................................................................................... 33
Une exigence de covariance des équations.................................................................................................................................................................... 33
Outils pour décrire des espaces ( temps) non Euclidiens ( Riemann, Christoffel, Ricci,.)........................................................................................ 33
Compatibilité avec la théorie de Newton ( champ faibles et faibles vitesse).............................................................................................................. 33
Quelqu'un de très motivé, voire opiniâtre et convaincu qu'il a raison ( EINSTEIN)................................................................................................. 33
4-Les fondements de la RG..................................................................................................................................................................................................... 34
5-Les Idées Nouvelles............................................................................................................................................................................................................. 35
1-Principe de Relativité générale: Extension du principe de relativité aux systèmes non galiléens, citons Einstein ( synthèse finale 1916) ( ref 2)............................................................................................................................................................................................................................................ 35
"Raisons qui suggèrent une extension du postulat de Relativité................................................................................................................................ 35
Elargissement du principe de relativité............................................................................................................................................................................ 35
2-Principe d'Equivalence.................................................................................................................................................................................................... 37
(Interprétation purement cinématique du champ de gravitation, possible si le tenseur de Riemann est nul dans le domaine considéré)....... 37
Masse Inerte.................................................................................................................................................................................................................... 37
Masse pesante................................................................................................................................................................................................................ 37
Le principe d’équivalence faible ( PEF)....................................................................................................................................................................... 37
Le principe d’équivalence d’Einstein ( PEE)............................................................................................................................................................... 38
Le principe d’équivalence fort*(PEF) , inclut l’énergie du champ gravitationnel lui même................................................................................ 38
Décalage spectral comme conséquence directe du PEE................................................................................................................................................ 40
La courbure nécessaire de l'espace temps....................................................................................................................................................................... 40
Moralité: Se ramener à un problème déjà résolu !!......................................................................................................................................................... 46
6-La mise en œuvre.................................................................................................................................................................................................................. 46
Rappel des transformations utilisées en RR (ref 4):....................................................................................................................................................... 46
Rappel :Vecteurs , Scalaires et Tenseurs en RR............................................................................................................................................................. 46
Ecriture des équations de Maxwell sous forme tensorielle........................................................................................................................................... 48
Définition de l'Impulsion en RR (ref 4)............................................................................................................................................................................. 49
Métrique en RR.................................................................................................................................................................................................................... 50
Généralisation des transformations.................................................................................................................................................................................. 51
La gravitation n’est pas linéaire, auto interaction : le graviton se couple avec lui même à la différence du photon).......................................... 51
7 - Géométrie de la relativité Générale , des concepts difficiles à se représenter........................................................................................................... 52
La métrique........................................................................................................................................................................................................................... 52
Les espaces Euclidiens sont supposés connus............................................................................................................................................................. 52
Espaces Riemanniens ( Variété Riemannienne).............................................................................................................................................................. 53
Le tenseur métrique Gij intervenant dans l'élément linéaire différentiel: ds²= Gij.dXi.dXj...................................................................................... 53
Propriétés du tenseur métrique et de la métrique associée:..................................................................................................................................... 53
-L'expansion de l'univers, de sa métrique entre 2 points quelconques de cette hypersurface................................................................................ 56
cf expansion..................................................................................................................................................................................................................... 56
- Effet de Courbure:............................................................................................................................................................................................................. 56
Définition du transport parallèle (cf outils)..................................................................................................................................................................... 58
Horizon cosmologique dans un Univers en expansion................................................................................................................................................. 58
C'est la formule de Robertson Walker ( postérieure à l’équation de Friedman)......................................................................................................... 61
Géométrie de la Relativité Générale : l’approche contemporaine ref 13....................................................................................................................... 62
Variétés................................................................................................................................................................................................................................. 62
Géodésique........................................................................................................................................................................................................................... 62
On dit alors que la variété possède une courbure, définie mathématiquement par le commutateur des deux dérivées covariantes :.............. 62
(dr Ds - ds Dr ) Vm = Rmnrs Vn. (dxr, dxs ) avec dr premier symbole de dérivation, Ds deuxième symbole..................................................................... 62
où = Rmnrs est le tenseur de courbure de Riemann......................................................................................................................................................... 62
Métrique............................................................................................................................................................................................................................... 64
La courbe la plus « courte » possible allant d’un point à un autre est solution de l’équation "des géodésiques" :.......................................... 64
d²Xk/ds²+ Gikj .(dXi/ds)(dXj/ds) =0.................................................................................................................................................................................... 64
On définit les symboles de Christoffel Gikj = 1/2(Glk )( ¶Gjl/¶xi + ¶Gil/¶xj - ¶Gij/¶xl )................................................................................................. 64
Courbure............................................................................................................................................................................................................................... 65
tenseur de Riemann : Rjikl = ¶Gijl/¶Xk - ¶Gijk/¶Xl +Gimk.Gmjl - Giml.Gmjk...................................................................................................................... 65
Le tenseur de Riemann étant le commutateur de 2 dérivées covariantes, sa dérivée covariante Di est nulle. Plus exactement on obtient l’identité de Bianchi :....................................................................................................................................................................................................... 66
Espaces symétriques.......................................................................................................................................................................................................... 67
Vecteurs de Killing :............................................................................................................................................................................................................ 69
8-Outils : Tenseurs, Calcul tensoriel..................................................................................................................................................................................... 70
Composantes contravariantes d'un vecteur X................................................................................................................................................................ 70
Composantes covariantes d'un vecteur X....................................................................................................................................................................... 70
Coordonnées curvilignes................................................................................................................................................................................................... 71
Repère naturel en M............................................................................................................................................................................................................ 71
Changement de repère en M (Changement de Coordonnées)..................................................................................................................................... 73
Elément linéaire de l'espace................................................................................................................................................................................................ 73
x.y= Gij.xi.xj avec Gij = êi.êj................................................................................................................................................................................................. 73
Problème fondamental de l’analyse tensorielle............................................................................................................................................................... 74
Connexion métrique............................................................................................................................................................................................................ 74
Dérivée covariante d'un vecteur....................................................................................................................................................................................... 75
Transport parallèle d'un vecteur....................................................................................................................................................................................... 75
Equation Géodésique cf ref 4 & 2..................................................................................................................................................................................... 76
Méthode 1 ( Géométrique la plus simple).................................................................................................................................................................... 76
Méthode 2 ( Méthode « physique » originale d’Einstein)...................................................................................................................................... 76
Rappel: Fonction de Lagrange du mouvement ( Lagrangien) en mécanique classique........................................................................................... 76
Fonction de Hamilton en mécanique classique(pm)...................................................................................................................................................... 77
Tenseurs............................................................................................................................................................................................................................... 77
Scalaires................................................................................................................................................................................................................................ 77
Quadrivecteur contravariant.............................................................................................................................................................................................. 78
Quadrivecteur covariant..................................................................................................................................................................................................... 78
Tenseur contravariant........................................................................................................................................................................................................ 80
Tenseur covariant............................................................................................................................................................................................................... 81
Tenseur mixte et de rang supérieur à 2............................................................................................................................................................................. 81
Quelques opérations utiles sur les tenseurs................................................................................................................................................................... 83
Jacobien d’une transformation.......................................................................................................................................................................................... 83
Densité de tenseur.............................................................................................................................................................................................................. 83
Dérivée covariante d'un tenseur....................................................................................................................................................................................... 83
Divergence covariante d'un vecteur................................................................................................................................................................................. 85
Divergence covariante d'un tenseur................................................................................................................................................................................. 85
Tenseurs particulièrement utilisés en Relativité Générale............................................................................................................................................. 86
Tenseur de Riemann Cf Ref 8 & 2&4................................................................................................................................................................................ 86
Tenseur de Ricci : cf ref 2................................................................................................................................................................................................... 89
Le tenseur de Ricci ( Cf ref 7 )contrôle la dérivée seconde du changement de volume, d'un petit volume lors de sa trajectoire géodésique. 89
Le tenseur de Weyl contrôle la déformation ( sphère/ellipsoïde)................................................................................................................................ 89
Scalaire de Ricci................................................................................................................................................................................................................... 89
Tenseur d'Einstein............................................................................................................................................................................................................... 90
Tenseur Impulsion Energie : Cf ref 7................................................................................................................................................................................ 91
9-Les Résultats......................................................................................................................................................................................................................... 92
Equation géodésique.......................................................................................................................................................................................................... 92
Retour sur l'équation de la gravitation d'Einstein........................................................................................................................................................... 92
Exigence de covariance pour conserver la même forme par changement de coordonnées..................................................................................... 92
La limite en l'absence de matière doit être la métrique de Minkowski......................................................................................................................... 93
Limite de Newton pour champ faible , stationnaire et vitesse faibles ( équation de Poisson)................................................................................ 93
Il y a une solution unique qui est le tenseur d'Einstein (cf identité de Bianchi)........................................................................................................ 93
Confirmations récentes de la Relativité Générale (1997)................................................................................................................................................ 96
Ondes gravitationnelles..................................................................................................................................................................................................... 96
Précession de Lense Thirring............................................................................................................................................................................................ 96
Effet Shapiro ( prédit en 1964)........................................................................................................................................................................................... 97
Précision de confirmation de la Relativité générale........................................................................................................................................................ 97
La solution de Schwarzschild s'obtient de la façon suivante:...................................................................................................................................... 98
10-L'élaboration laborieuse de la théorie.............................................................................................................................................................................. 99
11-L'approximation Newtonnienne...................................................................................................................................................................................... 100
11-1 Loi du mouvement (équation géodésique)........................................................................................................................................................... 100
11-1-b : Approximation Newtonnienne (synthèse)...................................................................................................................................................... 103
11-2 Approximation de la loi de Poisson........................................................................................................................................................................ 104
12- De la réalité physique des coordonnées en Relativité générale............................................................................................................................... 104
Changement de coordonnées.......................................................................................................................................................................................... 104
13- Conclusion....................................................................................................................................................................................................................... 107
14- Références Bibliographiques......................................................................................................................................................................................... 110
15 – Glossaire......................................................................................................................................................................................................................... 110
Présentation de la
théorie de la Relativité Générale
0- Préambule
1-Introduction
2-L'application à
la Cosmologie
3-Recette pour une théorie de la Relativité Générale
4-Les
fondements de la RG
5-Les Idées Nouvelles
6-La mise
en œuvre
7-Géométrie
de la relativité
Générale, des concepts difficiles
à se représenter
8-Les outils, tenseurs, Calcul tensoriel
9-Les
résultats
10- L'élaboration laborieuse
de la théorie
11- L'approximation Newtonienne
12-
De la réalité
physique des coordonnées en
Relativité générale
13- Conclusion
14- Références Bibliographiques
14- Glossaire
0 - Préambule
La relativité générale est
enseignée aujourd’hui dans le cadre d’un formalisme « ensembliste «
commun à la physique moderne.
La démarche, que j’ai suivie,
procède d’une approche plus historique, celle
qui a prévalu au moment de l’élaboration de la théorie qui m’a paru moins austère.
Dans tous cas la Théorie
débouche sur des conclusions qui « bouleversent »
nos habitudes de pensées déjà pourtant malmenées par la théorie de la
Relativité Restreinte.
La
relativité générale est enseignée aujourd’hui dans le cadre d’un formalisme
ensembliste commun à la
physique moderne. L’espace temps est une
Variété différentiable de type Riemannien, au
sens de la Topologie, dont on étudie les propriétés.
Ce formalisme procède d’une
volonté d’unification et de synthèse de ces
branches existantes dans le cadre d’une super théorie et cherche par
formalisation et abstraction à extraire les principes communs à ces différentes
branches et a en effacer les contradictions
apparentes. Cette méthode possède une puissance heuristique [F1]indiscutable
dans le cadre qu’elle vise.
Il m’a paru prématuré de
retenir cette approche, sauf pour certaines parties délicates décrivant la géométrie associée à la RG ou l’approche
contemporaine apporte quelques éclaircissements.
La démarche, que j’ai suivie,
procède d’une approche plus historique, celle
qui a prévalu au moment de l’élaboration de la théorie.
Cette
démarche possède également une puissance heuristique forte quoique différente
de celle actuellement retenue.
Rappelons
, que pour la Relativité
Restreinte la physique était en danger,
puisque après l’immense succès des équations de Maxwell unissant l’électricité
, le magnétisme et l’optique, l’expérience de Michelson remettait tout en
cause.
Pour la gravitation la
situation était moins critique, à part Mercure qui avait un comportement
inexpliqué (mais qui aurait pu s’expliquer par des perturbations d’astres non
repérés à l’époque), tout paraissait normal , sauf la
propagation « instantanée » de la gravitation. Mais des théories
s’inspirant de celles de l’électromagnétisme , étaient
en cours d’élaboration. C’est dire qu’il n’y avait pas urgence. C’est dans ce
cadre que la démarche historique, de nature épistémologique [F2]d’Einstein
aboutissant à la « découverte de la Relativité Générale » est intéressante
à étudier.
1- Introduction
Après avoir vainement , pendant plusieurs années tenté d'adapter
la gravitation dans le cadre de la RR (Espace temps de Minkowski ), Einstein,
vers 1913, en rupture avec ses idées
précédentes, abandonne le concept de force pour la gravitation et d'espace
temps de Minkowski pour le cadre et élabore une toute nouvelle théorie: La
théorie de la Relativité Générale qui se résume
(complétude)
à une seule équation ( cf Newton,
Einstein, Hilbert
)
Smn=k.Tmn
Smn= Tenseur d'Einstein, k
constante d’ajustement, Tmn = Tenseur Energie Impulsion
qui signifie que localement la géométrie de l'espace-temps représentée par le tenseur d'Einstein "S "est conditionnée par l'énergie localement présente ( sous toutes ses formes ) représentée par le tenseur "T". Cette formulation stigmatise le caractère primordial de la géométrie (métrique-connexion métrique
)..Cette assertion brutale présente
quelques petites subtilités qui méritent d'être explicitées
- Théorie de la gravitation ( ne concerne
pas les autres interactions)
La Relativité
Générale ( ¹RR ) est une théorie " Classique et Macroscopique " de la
gravitation. Le principal de ses deux piliers , le principe
d'équivalence
lié à l'égalité stricte de la masse pesante ( charge gravitationnelle) et de la
masse inerte ( énergie) ( testé à 10-12 aujourd’hui, STEP à 10-17
) ne s'applique qu'à la gravitation.
A noter
d'autres particularités de la gravitation par rapport aux autres interactions :
Son extrême faiblesse. (10 –41
fois plus faible que l’électromagnétique)
Son universalité : (pas de charge
nulle)
- La gravitation n'est
pas une force ( FAQ 1)
(Rappel Relativité Restreinte )
Cela présente deux aspects en interaction profonde et une remarque.
1-La courbure de l'espace temps , manifestation
de la gravitation , agit sur la matière et l'énergie
- Les corps* qui suivent des trajectoires courbes au voisinage de masses, ne font que suivre les géodésiques (chemins naturels de moindre effort).
2-La matière et
l'énergie, représentées par le tenseur énergie impulsion, courbent l'espace
temps.
- La courbure de l’espace est source
d’énergie (gravitation) donc sujet à la gravitation(nl) .
Rappel RR : Rappelons que la
Relativité Restreinte avait été développée pour rendre compte de l'invariance
des lois de l'électromagnétisme. La RR a permis bien d'autres découvertes, y compris en mécanique quantique, spin, anti matière etc..
Gravitation : Son extrême faiblesse.
Si l'intensité de l'interaction forte =1,
électromagnétique = 10-2, électrofaible= 10-5,
gravitation = 10-39. (ref
Barrow : la grande théorie)
.A noter que la comparaison d’intensité entre forces et gravitation n’est
pas évidente.
Gravitation : Son universalité
Alors que les autres interactions s'appliquent de façon
sélective aux particules, la gravité s'applique à toutes les formes de matière
et d'énergie ( même celle qu'on ne connaît pas comme
la mystérieuse matière noire qui pour l'instant ne semble se manifester que par
son effet gravitationnel) : Pas de charge gravitationnelle nulle.
Lumière
* y compris la lumière, qui a une masse en vertu de l'équivalence matière
énergie, ce qui semble ébranler l'hypothèse de la constance de sa vitesse
(direction) au sens de la RR (en fait dans le cadre de la théorie de la RG qui
est généralement covariante,
la signification physique de cette vitesse dépendant des coordonnées est
considérée comme douteuse).
Espaces non Euclidiens
Equations Covariantes
-
La notion de covariance, nécessaire pour satisfaire le principe de Relativité générale, est également obscure pour plus
d'un. Sa propriété fondamentale est de
conserver la forme des relations donc les équations ,
donc les lois par tout changement de coordonnées.
La signification
profonde de ceci est que les phénomènes physiques ont une réalité physique
propre, qui ne dépend pas de l'observateur, c'est à dire du système de
coordonnées qui n'est qu'un moyen arbitraire de les décrire, "sous un
certain angle". La description doit donc s'en affranchir.
-
Cette méthode se révèle très pratique pour
généraliser les lois :
-
Pas de Calcul et c’est
normal ! ! !
Enfin la cerise ( sur le gâteau) :
Métrique variable en fonction du temps ( FAQ2)
-
Le fait que comme conséquence des équations, la métrique
( invariant fondamental qui sert à mesurer la distance
entre deux points de l'espace temps) soit variable
en fonction du temps est également source de confusion , car cela choque
nos concepts habituels : lorsque des objets s'éloignent nous pensons qu'ils le
font toujours par un mouvement propre par rapport à un référentiel.
-
La c'est le référentiel qui change!!
« Fuite » des
Galaxies en 2D ( x en horizontal,t en vertical ) ref : Wright
Coordonnées synchrones Coordonnées
Lorentz
Et cela, ce n'était pas prévu
au programme !!Suite
FAQ1 : Qu’est
ce que cette hypothèse farfelue ? : En quoi fait elle avancer les
choses (simplicité du modèle). Réalité physique ? : Prédictions du
modèle vérifiables
Paradoxalement
, on est amené presque naturellement (cf ref 12) à cette conclusion, qui se révèle par ailleurs
d'une simplicité diabolique pour rendre compte de tous les phénomènes où la
gravitation intervient. Autre
conséquence: On ne sait pas associer de tenseur énergie Impulsion à la
gravitation (lié à sa nature particulière), difficulté de définir l'énergie lié
par exemple aux ondes gravitationnelles. A noter que Riemann a été le
premier à montrer ( 50 ans avant Einstein) que la courbure de
l'espace s'apparentait à une force. Par contre,
il a traité cet aspect sous un angle purement mathématique, sans aucune idée
sur les lois liant les phénomènes physiques et cette courbure. Le mathématicien
anglais W. Clifford qui traduisit la conférence
célèbre (1854) de Riemann pour la revue "Nature" en 1873 reprit et
amplifia ces idées ( On a space theory
of matter: Proceedings of
Cambridge Philosophical society 2 -1876). Voir aussi
théories concurrentes (Mie, Weyl,..)
FAQ2 : Qu’est ce encore que ce concept bizarre ? N’est
pas un artifice pour résoudre les contradictions de la relativité générale ( « c » peut
être dépassé, n’est plus constant ?).
A tel point qu'Einstein,
persuadé que l'univers était statique ( En 1916
il était limité à notre galaxie) , ne trouvant pas de solution avec ses
équations, modifie ses équations pour ajouter un
terme (L la constante Cosmologique ) qui lui permet de trouver une solution statique.
Pas sectaire, en 1927 il attirera l'attention de Lemaitre
sur les travaux de Friedmann
La puissance de la théorie de la
Relativité générale doit
s'évaluer non seulement aux problèmes non résolus (ex: périhélie de Mercure)
qu'elle permet de solutionner mais encore plus aux prédictions nouvelles,
inattendues et révolutionnaires qu'elle révèle.
Au sujet de la métrique variable, illustrons la par une
parenthèse Cosmologique (ref
6)
VB = dOB/dt = 3/dt, VA = dOA/dt = 6/dt
= 2 VB
***Age de
l'univers T = 2/3Hcrit
*****Pendant l'ère
radiative cette loi était : e= (t/ta)1/2
Fin de parenthèse
Cosmologique
Ce qu'en dit Einstein (ref
2)
"A la
lumière des connaissances acquises, ce à quoi nous avons eu la chance d'aboutir
apparaît comme presque évident:
un étudiant intelligent est capable de le comprendre sans grand effort" :
Limpidité
de la démarche : Deux principes seulement pour une équation
Cette déclaration euphorique d'Einstein appelle un commentaire.
*Tout se déduit de deux
principes ( comme en RR ) et de deux principes
seulement
- Généralisation du principe
de Relativité de la RR aux systèmes en mouvement
relatif accéléré: On augmente
la portée et donc la puissance du principe de Relativité
-
Principe d'équivalence
Du fait de l’égalité stricte de la masse pesante ( charge
gravitationnelle) et de la masse inerte ( quantité d’énergie), un champ local
gravitationnel est équivalent à un mouvement accéléré et réciproquement un
référentiel en chute libre dans un champ gravitationnel est équivalent à un
système inertiel. Ceci va permettre un traitement « cinématique » de
la gravitation. ( Calculs de changement de
référentiel).
-
Le Principe d’équivalence se décline
en 3 versions Faible, d’Einstein, et Fort
Le reste n'est que
de la cuisine ( un
peu lourde il est vrai) mathématique
De façon
lapidaire on peut dire que:
Avec Newton si on
retire la matière de l'univers, il reste l'espace et le temps!
Avec Einstein, si
on retire la matière (énergie ) de l'univers il ne
reste plus rien !
De ce fait les concepts
d’espace et de temps posé par Kant comme « données immédiates à priori de
la conscience » investis à ce titre
d’une réalité objective externe (divine dans le contexte de Kant) se réduisent
à leur stricte définition ( un outil du cerveau
indispensable à la compréhension du Monde)
Homogénéité et
Cohérence
Le fait qu'elle soit l'œuvre d'une seule personne lui
confère homogénéité et cohérence.
Complexité opératoire: Des outils complexes
Einstein a du
les étudier, se faire aider par
son ami Grossmann, et cela lui a coûté beaucoup de
temps et d'errements comme en atteste ses écrits et publications.
Citons le philosophe Mach qui l'a beaucoup influencé.
Paradoxalement Mach n'a jamais cru à la RG.
Succès et fécondité
Ce fut le début du
modèle standard avec tous ses développements qui vont bien au delà de la RG.
2-
L'application à la Cosmologie
Rappel: Avec Newton quand on retire la
matière, il reste l'espace et le temps,
Avec Einstein quand on retire la matière
, il ne reste rien ( ou presque)
Einstein équation originale Poisson
( Newton)
Rmn-(gmn.R)/2=0 D(F) = 0 en l'absence de
matière
Rmn-(gmn.R)/2= - 8p.G.Tmn , ou Rmn= -
8p.G.[Tmn -(gmn.T)/2], D (F)
=4pG.r
dans la matière
Einstein équation modifiée
Rmn-[gmn(R-2L)]/2=0
D(F) = 0 en l'absence de
matière
Rmn-[gmn(R-2L)]/2=
- 8pGTmn D (F) = 4pG.r dans la matière
Tenseur d'Einstein, Tenseur, Divergence d'un Tenseur
Tenseur Ricci, Scalaire de
Ricci, Tenseur Métrique, Constante Cosmologique
Contraction de Tenseur ,Tenseur de Riemann, ,Dérivée covariante de tenseur, Espaces Riemanniens
Déplacement parallèle curviligne, Coordonnées curvilignes, Connexion
Métrique
Coordonnées contravariantes,
Covariantes,, espaces vectoriels/duals,
etc …..
Quelques définitions (
provisoires):
Qu'est ce qu'un
tenseur ?
|
|
êR00
|
R01
|
R02
|
R03ê
|
|
|
êR10
|
R11
|
R12
|
R13ê
|
Rmn =
|
êR20
|
R21
|
R22
|
R23ê
|
|
|
êR30
|
R31
|
R32
|
R33ê
|
Une équation
entre de tels tenseurs de rang 2 génère 16 équations (
puisque tout les termes de même indice mn des tenseurs doivent être égaux entre eux). A noter que
si le tenseur est symétrique le nombre d’équations indépendantes est plus
faible. Cette définition
sera précisée.
Comment
modéliser la répartition de l'énergie au niveau de l'Univers ?
p sa pression, on obtient alors le Tenseur Impulsion Energie
suivant
Qu'est ce qu'une
métrique ?
La métrique est l’élément clé de la RG, sa forme caractérise la géométrie
de l’espace temps.
L'équation de la gravitation ne permet en fait que d'en déterminer les paramètres.
Quelle métrique utiliser ? ( en Cosmologie)
C'est la métrique
régie par le ds² de Robertson Walker (RW),
ds²= dt²
-R²(t)[dr²/(1-kr²)
+ r²( dq²+
sin²q.dj²)]
qui correspond
au tenseur métrique gmn ci dessous ( on verra comment on l'établit plus
loin)
gmn = 0 si m est différent de n, k=1 ( hypersphère) ou 0 ( plat), ou
-1(hyperbolique). Pour
d’autres distributions de matière, autres métriques (Schwarzschild pour symétrie centrale
par ex )
Comment déduire de
l'équation tensorielle de la gravitation des équations classiques
êR00 0 0 0ê | 1 | êT00 0 0 0 ê
ê R11 0 0ê+ ½(R-2L)
.| -R²/(1-kr²) | =
- 8pG. ê0 T11 0 0 ê
ê R22 0ê |
-R²r² | ê0 0 T22 0 ê
ê R33ê | -R²r²sin²q | ê0 0 0 T33 ê
Rmn = Tenseur de
Ricci gmn=Tenseur
Métrique Tmn= Tenseur Impulsion/E
Tenseur de Rici: Rmn= ¶Gmln/¶xl- GmlsGnsl , scalaire de Ricci: R=gmn. Rmn,
Tmn=(p+r)Um.Un - p.gmn
et Gmln = 1/2(Gsl )( ¶Gns/¶xm + ¶Gms/¶xn - ¶Gmn/¶xs )
On obtient alors les deux (compte tenu de l'isotropie spatiale
en x,y,z) équations ci dessous
(2/R)(d²R/dt²)+(1/R²)(dR/dt)²+Kc²/R² -L.c²=
-8pGp/c² (1)
(3/R²)(dR/dt)²+3Kc²/R² - Lc²=
8pGr (2)
p pression du "fluide
" cosmique,
K constante de courbure ( +1, 0 ou -1),
Nous disposons
alors de tous les éléments pour décrire le modèle Cosmologique.
Quelques modèles très
simples
Modèle statique
d'Einstein
a) avec
l'équation d'origine ( sans constante cosmologique):
2/R(d²R/dt²)+1/R²(dR/dt)²+K.c²/R² = -8p.G.p/c² (1)
3/R²(dR/dt)²+3K.c²/R² = 8p.G.r (2)
Comme R= R0
est constant et p= 0 , l'équation 1 donne : c²/R² = 0 !!!
,
l'équation 2 donne : 3c²/R² =8pGr !!!
Cela laissa Einstein perplexe, qui jetant aux orties la limite
Minkowskienne lorsque l'espace est vide rajouta la constante Cosmologique
Rmn-[gmn(R-2L)]/2= - 8pGTmn d'ou on tire:
2/R(d²R/dt²)+1/R²(dR/dt)²+K.c²/R² -L.c²=
-8pG.p/c² (1)
3/R²(dR/dt)²+3K.c²/R² - Lc²= 8p.G.r (2)
La deuxième donne : 2c²/R0² =8pGr
On en déduit
: R0 = c/(2(pGr)1/2
Certains lui font jouer un rôle dans l'hypothèse
d'inflation primordiale.
Bref, pour une bévue, un beau sujet de controverse.!!!
2- Modèle de De Sitter ( Univers vide)
Cette fois ci le rayon n'est plus supposé constant R(t)
Si p=r=0 et K
=0 , les équations se simplifient considérablement ( ne
sont plus indépendantes)
Univers vide : d²R/dt²- Lc²R/3 = 0
La solution est évidente R(t)= R0. e
.t. (Lc²/3)^1/2 ( Inflation exponentielle)
Annexe 1 :Méthode de calcul
pour modèle De sitter
Gij = 0 si i est
différent de j
De la formule : Gikj =
1/2(Glk )( ¶Gjl/¶xi + ¶Gil/¶xj - ¶Gij/¶xl )
G 011
= (G11)/(2)(¶G11/¶x0
+ ¶G01/¶x1
- ¶G10/¶x1)
=
(G11)/(2)(¶G11/¶x0 ) = -((1-kr²)/2R²)(2R.R'/1-kr²) = R'/R
On calcule les autres symboles de Christoffel G ( beaucoup
sont nuls)
On reporte ces symboles dans le tenseur de Ricci qui vaut
si [-g]1/2 =-1
On calcule le scalaire de Ricci à partir du tenseur de
Ricci qu'on multiplie par Gij
On multiplie le scalaire de Ricci par la métrique et
Itou pour le terme avec la constante cosmologique L
On obtient ainsi le membre de gauche de l'équation
Dans le
modèle standard complet on peut utiliser une autre équation déduite
d/dt(R3.r) + p/c²(d/dt(R3)) =0 (3)
-
Ces modèles sont plus complexes et
justifient un exposé dédié. (cf exposé sur
Cosmologie).
3-Recette pour une
théorie de la relativité générale
Disposer d'une théorie de Relativité restreinte comme modèle à généraliser
Idées de généralisation du principe de relativité
Principe
d'équivalence
Outils pour opérer des changements de coordonnées très
généraux ( Calcul tensoriel)
Une exigence de covariance des équations
Outils pour décrire des espaces ( temps)
non Euclidiens ( Riemann, Christoffel, Ricci,.)
Compatibilité avec la théorie de Newton (
champ faibles et faibles vitesse)
Quelqu'un de
très motivé, voire opiniâtre et
convaincu qu'il a raison ( EINSTEIN)
4-Les fondements
de la RG
Quelle
expérience permet de prouver que c'est A qui tourne et non pas B ( en sens contraire).
Il y a le
fameux argument des masses distantes (principe de Mach).
5-Les Idées
Nouvelles
1-Principe de Relativité générale: Extension du
principe de relativité
aux systèmes non galiléens, citons Einstein ( synthèse
finale 1916) (
ref
2)
"Raisons qui suggèrent une extension
du postulat de Relativité
Soit deux corps fluides de même taille et de même
nature flottant librement dans l'espace et
si éloignés l'un de l'autre et des autres corps de l'espace que les seules forces de gravitation à prendre en compte sont celles qu' exercent l'une sur l'autre les parties d'un seul de ces
corps. On suppose que la distance entre les deux corps ne varie pas et que les
parties d'un corps n'ont pas de mouvement relatif. Mais supposons que chaque
masse, du point de vue d'un opérateur au repos par rapport à l'autre, ait un
mouvement de rotation
à vitesse angulaire constante autour de la droite reliant les deux masses. Et supposons qu'en
arpentant les corps on trouve que l'un a la forme d'un ellipsoïde
et l'autre d'une
sphère. Demandons
nous pour quelle raison les corps se comportent différemment
. /..../Une réponse satisfaisante à cette question doit pouvoir être vérifiée expérimentalement. La mécanique Newtonienne qui fait
référence à l'espace
"absolu "-attaché à celui qui est sphérique ne convient pas. Cet espace non décelable physiquement correspond à une cause fictive. Une réponse satisfaisante ne peut
s'énoncer qu'ainsi.
Elargissement du principe de relativité
2-Principe d'Equivalence : Idée la plus féconde, énoncée
dès 1907 ( mais pas encore sous ce nom qui apparaîtra en 1911), qui dit qu'un champ gravitationnel peut être
localement simulé ( ou compensé) par un mouvement accéléré et réciproquement.
(Interprétation purement cinématique du
champ de gravitation, possible si le tenseur de Riemann est nul dans le domaine
considéré).
Masse
Inerte
La relativité restreinte éclaire ce
point: dE= d(mc²) = m0.c².d ( 1-v²/c²)1/2
C’est le sens profond de l’équation
F= mi. g
Masse
pesante
A priori rien ne
relie ces deux paramètres.
Le
principe d’équivalence faible ( PEF)
Etabli par Galilée et Newton, il est
relatif aux champs statiques et uniformes pour la matière.
Le
principe d’équivalence d’Einstein ( PEE)
Reprenant les résultats de la relativité
restreinte, la masse inclut toutes les formes d’énergie.
Le
principe d’équivalence fort*(PEF) , inclut l’énergie
du champ gravitationnel lui même.
La remarque
précédente s'applique aussi au cas de deux corps en interaction
gravitationnelle.
Donc la
gravitation se couple aussi, avec l'énergie du champ gravitationnel.
La Relativité
générale obéit au PEF, illustrons ceci :
* Certains auteurs
contestent l'intérêt de cette distinction pour eux PEE --->PEF
On en déduit
immédiatement, la courbure des rayons lumineux, le décalage spectral, le
ralentissement des horloges dans un champ de gravitation ,
car c'est évident dans le système accéléré (ref 4).
Décalage spectral comme conséquence
directe du PEE
Considérons la prédiction célèbre du PEE du décalage gravitationnel vers
le rouge.
Au temps t0, la boite de traîne
émet un photon de longueur d'onde l0
Pendant ce temps les boites ont acquis une vitesse additionnelle dv = adt = az/c
En
conséquence le photon atteignant la boite de tête subit un décalage vers le
rouge lié à l'effet Doppler classique de
|
dl/l0 = dv/c =az/c² |
|
On suppose v/c
petit, pour travailler au premier ordre.
Conformément au PEE , le même phénomène
doit se produire dans un champ de gravitation uniforme.
La courbure nécessaire
de l'espace temps
Imaginons
une tour de hauteur z située sur une planète , munie
d'un champ de gravitation d'intensité ag ( accélération due à la gravitation
en mécanique classique)
Cette
situation est réputée non distinguable
de la précédente, du point de vue d'un observateur dans une boite au sommet de
la tour ( capable de détecter le photon , mais coupé
du monde extérieur)
En
conséquence, le photon émis depuis le sol avec une longueur d'onde l0 doit
être décalée vers le rouge de:
dl/l0 = agz/c²
C'est
le fameux décalage vers le rouge gravitationnel, conséquence directe du PEE,
sans avoir besoin des équations de la Relativité générale. Il a été vérifié
expérimentalement d'abord par Pound et Rebka en 1960.
Ils ont utilisé l'effet Mössbauer pour mesurer le changement de fréquence de
rayons g dans cette configuration au
Jefferson Labs à Harvard.
L'effet gravitationnel de décalage vers le rouge amène un autre
argument en faveur de la courbure de l'espace.
Représentons un diagramme spatio-temporel de
l'expérience précédente
Cf : http://www.astro.ucla.edu/~wright/relatvty.htm ou
http://nedwww.caltech.edu/level5/march01/Carroll3/Carroll4.html
![]()

![]()
![]()
![]()
![]()
![]()
![]()
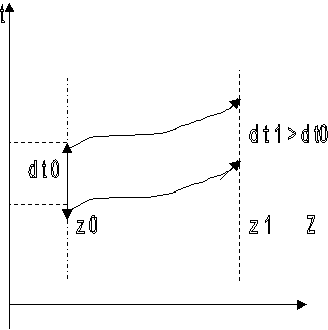
Le
physicien au sol émet un rayon lumineux de longueur d'onde l0 d'une
altitude z0, qui voyage
vers le sommet de la tour d'altitude z1.
Le
temps entre deux crêtes de l'onde émise est dt0 = l0 /c, et le même intervalle pour la détection est dt1
= l1 /c.
Comme le champ est statique les chemins spatio
temporels du début et de la fin de
l'intervalle sont strictement parallèles ( ne dépend
pas du temps d'émission)
On
l'a représenté par une courbe quelconque ne représentant pas nécessairement le
chemin réel, car là n'est pas le propos.
La
géométrie élémentaire voudrait que les temps dt0
et dt1
soient les mêmes.
Ce
n'est pas le cas, du fait du décalage gravitationnel vers le rouge qui implique
que dt1
> dt0, que
l'on peut interpréter comme le fait que
l'horloge au sommet bat plus vite
Ou est l'erreur ?
Notre
géométrie simple ( Euclidienne) ne s'applique pas et
on doit appliquer une géométrie correspondant à un espace courbé ( l'échelle de
temps n'est pas uniforme sur le diagramme, elle dépend de z, pour z1
, l'échelle est plus petite que pour z0.
Tout
ceci nous incite à penser qu'en présence de la gravitation, l'espace temps doit
être pensé en terme de Variété courbe.
Cela confirme que plus on est haut dans
le champ plus les horloges battent vite.
Exemple: le
ralentissement des horloges en relativité générale dans le champ de gravitation
terrestre est égal à celui en RR d'un système animé d'un mouvement uniforme d'une vitesse égale à la
vitesse de libération ( 11,2 km/s,
). On peut l'illustrer de façon non rigoureuse par le principe d'équivalence. ( Considérer un observateur qui depuis l'espace lointain
tombe, dans le champ de gravitation terrestre ( référentiel inertiel), à l'approche de la surface sa vitesse sera de
11,2 km/s. Il
allume ses rétro fusées pour se poser en douceur, ceci se traduit pour lui par
une accélération conduisant à une vitesse de 11,2 km/s,
il compare ses observations, à vous de finir. )
Le recours à une courbure de
l'espace temps en lieu et place de force s'appuie également sur l'argument
suivant. Si une force produit une accélération remarquons que la définition rigoureuse de l'accélération produite par la gravitation seule, est impossible à définir, du fait
de l'absence de charge
gravitationnelle nulle. On ne peut pas comparer l'effet de la
gravitation sur un objet de charge nulle de masse inerte mi et un
objet de charge gravitationnelle mg et de même masse mi , puisque mg est toujours proportionnel
à mi.
Par contre on sait définir rigoureusement le référentiel chute libre
qu'on soit en présence ou non d'un champ de gravitation (référentiel inertiel
ou les lois de la RR s'appliquent).
D'autre part le PEE ou PEF
nous incite à penser que si les autres lois de la physique continuent d'être
les mêmes dans un champ de gravitation auquel elles sont soumises ( tout ce qui existe à une masse), c'est que la géométrie de
l'espace dans lequel elles se déroulent a été déformé , toutes choses égales
par ailleurs. Cette explication est très cohérente et rend simplement bien
compte du phénomène et illustre son universalité.
La voie pour établir les
lois en Relativité générale est alors toute tracée.
Notre
tâche est de montrer comment les autres lois de la physique ,
autres que celles gouvernant la chute libre des corps sont affectées par la
courbure de l'espace temps.
Le
paradigme suivant est utilisé. Puisque les particules en chute libre ( non soumises à d'autres interactions que le champ
gravitationnel) suivent les géodésiques de l'espace temps, et que conformément
au PEF c'est équivalent à un système inertiel, prenez les lois de la physique
dans un espace Euclidien écrites classiquement en termes de dérivées partielles
(les lois exprimées dans le cadre de la Relativité Restreinte).
Dans
la Variété topologique différentiable représentant l'espace temps de la
Relativité générale, le référentiel chute libre correspond à l'espace Euclidien
tangent localement , donc ces lois de la RR
correspondent à celles exprimées en coordonnées Normales Riemanniennes (CNR) de
la Variété, coordonnées dans lesquelles elles prennent la forme canonique de la
RR.
Traduisez
ces lois en termes de relations entre tenseurs via
une équation tensorielle covariante ,
en changeant par exemple les dérivées
partielles en dérivées covariantes.
Du
fait des propriétés des tenseurs, cette version sera alors valide ( localement) dans n'importe quel système de coordonnées qui
transforme les CNR en coordonnées quelconques via la transformation
généralisée locale .
Cette
procédure est quelquefois appelée le principe de covariance, ce qui est un peu
excessif, car c'est en fait une pure conséquence du PEE avec la condition mathématique complémentaire que ces lois doivent
être indépendantes du système de coordonnées.
Un
autre nom pour cette règle est le point virgule remplace la virgule, du fait
des conventions utilisées pour les dérivées partielles "," et les
dérivées covariantes";"
Notons que le principe de Relativité Générale qui s'est révélé
d'une puissance heuristique décisive n'est en fait pas nécessaire du moins en
tant que postulat car :
L'exigence
d'avoir des lois indépendantes du système de coordonnées est incontournable.
Si
on réalise une expérience, les résultats de cette
même expérience vus par deux observateurs utilisant des systèmes de
coordonnées différents, pour la décrire , doivent être
les mêmes.
Il y a nécessairement une représentation des équations qui traduit
ce fait (sinon mal formulé).
![]()
 Un bémol, un système « chute libre », n'est
équivalent à un système inertiel que localement et on ne peut pas l’étendre à
l’infini contrairement aux systèmes galiléens (rappel de l’arpentage
/chronométrage en RR). En RG, la structure de métrage d ‘extension du
référentiel ( on peut imaginer un treillis construit
avec des barres « rigides »), dans un champ de gravitation central,
serait soumis à un effet de marée et
déformée,(mouvement relatif). D’ou la difficulté de parler d’une vitesse
d’un objet distant. Les repères galiléens de la Variété sont déconnectés. Il
faut définir le transport parallèle, mais il dépend du chemin suivi!. Préciser les conventions.
Un bémol, un système « chute libre », n'est
équivalent à un système inertiel que localement et on ne peut pas l’étendre à
l’infini contrairement aux systèmes galiléens (rappel de l’arpentage
/chronométrage en RR). En RG, la structure de métrage d ‘extension du
référentiel ( on peut imaginer un treillis construit
avec des barres « rigides »), dans un champ de gravitation central,
serait soumis à un effet de marée et
déformée,(mouvement relatif). D’ou la difficulté de parler d’une vitesse
d’un objet distant. Les repères galiléens de la Variété sont déconnectés. Il
faut définir le transport parallèle, mais il dépend du chemin suivi!. Préciser les conventions.

Moralité:
Se ramener à un problème déjà résolu !!
Exemple
de changement de coordonnées: le mouvement des planètes vu de la Terre ( référentiel x,y,z) et le même mouvement vu du Soleil
(référentiel x',y',z')
6-La mise en œuvre
Cette notion de transformation de
coordonnées est essentielle pour bien comprendre la démarche de la RG.
Rappel des
transformations utilisées en RR (ref 4):
Si un référentiel 1 est
caractérisé par ses coordonnées Xi
, i de 0 à 3 ( X0 pour t et X1,X2,X3
pour x ,y ,z ), le référentiel 2 animé d'un mouvement uniforme ( par exemple //
à X1) par rapport à 1 est caractérisé par ses coordonnées X'
j , j de 0 à 3 ).
Le groupe de
Lorentz ( qu'on
peut représenter par une matrice 4x4 : Lij),
permet de passer de Xi à X'i par X’j
= Lij Xi = åi Lij Xi ( Convention d’Einstein sommation sur indice haut/bas
répété )
Ce groupe qui conserve par principe la métrique ( ds²= c²dt²- (dx²+dy²+dz²)) est l'équivalent du groupe des rotations
dans l'espace 3D ( termes en Cos a, Sin a de la matrice de rotation remplacés par cosh z, sinh z ).
Lij
vaut si on pose g = (1-b²)-1/2 et b=v/c=tanh z
êCosh z, -Sinh z, 0 0ê êg, -bg,0,0ê ç1 0 0 0 ç
ê-Sinh z,Cosh z, 0 0ê= Lij = ê-bg, g, 0,0êet h=LT.h. L = ç0 -1 0 0
ç
ê0 , 0 , 1 0ê ê0,
0,1, 0ê ç0 0 -1 0
ç
ê0 0 0 1ê ê0 0 0 1ê ç0 0 0 -1 ç
Cette transformation linéaire s'applique à tout
le référentiel.
Elle a la propriété de conserver invariantes les
équations de Maxwell ( elle a été fait pour!)
Annexe 2
Rappel :Vecteurs , Scalaires et
Tenseurs en RR
Un ensemble de 4 valeurs qui
se transforme par le groupe de Lorentz comme les différentielles dXi (dXi) est appelé
un quadrivecteur contravariant
(covariant).
Une valeur comme ds² qui est invariante est appelée quadriscalaire ou
scalaire de Lorentz.
Un exemple de quadrivecteur covariant est le gradient d'une fonction scalaire.
On peut transformer un quadrivecteur contravariant en
quadrivecteur covariant en le multipliant par le tenseur métrique ( Ai=Mij.A^j)
L'intérêt
de ces quadrivecteurs et quadri scalaires en RR est que si on peut écrire des
lois de la physique avec ces objets, ces lois sont
valables pour tous les systèmes inertiels conformément
au premier postulat de la RR.
Ils sont appelés manifestement covariants.
Ceci se généralise aux
tenseurs d'ordre supérieurs.
Ecriture des équations
de Maxwell sous forme tensorielle
Le vecteur champ électrique E et le vecteur champ magnétique B sont alors les composantes d'un tenseur Fij de rang 2, antisymétrique construit à partir des
dérivées partielles de Ai.
Rappel forme Classique Ñ.E=4pr,
ÑxB-¶tE = 4pJ
quadri potentiel Ai (i de 0 à 3) ÑxE+¶tB=0
Ñ.B=0
Forme
Relativiste
½ 0 Ex Ey
Ez ½
Fij
= ½-Ex 0
Bz -By ½
½-Ey -Bz 0
Bx ½
½-Ez By -Bx 0 ½
Fij
= dAi/dxj-
dAj/dxi,
les équations de Maxwell (4), (5) s'écrivent:
¶kFij
+ ¶iFjk
+ ¶jFki
= 0 soit ¶(kFij) =0 (RR)
ÑiFij
=4p Jj (RG)* (4)
Ñ(kFij)
=0 (RG)* (5)
Quadrivecteur Jj
= (r,J) , r = densité de charge et J trivecteur densité
de courant (x,y,z)
Sous cette forme elles sont naturellement invariantes par tout changement de
coordonnées par le groupe de Lorentz (6 paramètres ou de Poincaré 10
paramètres).
*On verra plus loin, que sous cette
forme, il suffit de remplacer la dérivée partielle par une dérivée covariante pour étendre
leur validité à la Relativité générale
Définition de
l'Impulsion en RR (ref 4)
Elle est représentée par un quadrivecteur
Pi
P0=E/c, P1=Px, P2=Py, P3=Pz ( P0 est la
composante de l'impulsion dans la "direction" du temps, Px,Py,Pz sont les composantes
d'espace)
Avec
E énergie totale de la particule : E =gmc² et P= gmv ( m masse au repos, g= (1-v²/c²)-1 )
C'est cette définition qui
sera reprise et généralisée dans le tenseur Energie Impulsion de l'équation
d'Einstein
Métrique en RR
La métrique en RR est
celle d'un espace de Minkowski de signature +1,-1,-1,-1 ( pseudo Euclidien).
Elle s'écrit sous forme d'un tenseur d'ordre 2, diagonal, hab
(4x4) tel que h00=+1,
h11=h22=h33=-1( les autres termes sont nuls).
On trouve aussi la convention inverse –1,+1,+1,+1
Certains résultats établis en
RR vont être repris en RG: Il s'agit de:
ds²=hab.dXa.dXb avec hab tenseur métrique Minkoswski
et hij. Lia .Lib
= hab
ç1 0 0 0 ç
ç0 -1 0 0 ç
ç0 0 -1 0 ç
ç0 0 0 -1 ç
d²t=hab.dXa.dXb avec dt temps propre ( associé au référentiel qui contient la
particule en mouvement, donc au repos), dt est un invariant par rapport aux transformations de
Lorentz
A noter que ds et dt sont identiques, au facteur c près, et comme pour simplifier on prend
c=1 on trouvera tantôt l'un tantôt l'autre ( paramètre
affine).
On
définit un vecteur quadri-vitesse
Vi
=dXi/dt
d²Xi/dt²=0 :
exprime que l'accélération est nulle dans les
systèmes inertiels.
Généralisation des transformations
En
RG une transformation locale plus générale des coordonnées doit être utilisée.
En
fait cette transformation locale est la plus générale possible appliquée à un
continuum espace temps ( une Variété différentiable de
dimension « n » admet localement Rn
comme espace tangent, et les relations
vont pouvoir s’exprimer en coordonnées Riemanniennes normalisées ).
La transformation est locale
car seules les dérivées partielles premières
des nouvelles coordonnées par rapport aux anciennes interviennent ( les dérivées d'ordre supérieur sont supposées infiniment
petites par rapport aux dérivées premières lorsqu'on tend vers 0)
dXi = Aij.dYj
Avec Aij
= ¶Xi/¶Yj
Ce
type de transformation conduit naturellement à utiliser une forme tensorielle
pour les relations, puisque les tenseurs opèrent des combinaisons linéaires sur
les composantes des vecteurs et vont posséder la propriété de conserver la
forme des relations.
Cette transformation n’est linéaire que localement. A plus large
échelle elle est hautement non linéaire avec des implications sur la structure
de « l’espace temps »
La gravitation n’est
pas linéaire, auto interaction : le graviton se couple avec lui même à la
différence du photon)
7 - Géométrie de la relativité Générale , des concepts difficiles à se représenter
La métrique
C'est le concept
clé de la relativité générale.
Rappelons que cette forme quadratique , invariante par changement de coordonnées
caractérise la structure de l'espace ( La topologie en est un autre aspect dont
la RG ne tient pas compte).
Les espaces Euclidiens sont
supposés connus.
Dans
un tel espace à n dimensions l'élément métrique vaut
ds²= Gij.dXi.dXj
avec Gij=Gji ( par construction puisque c'est le produit scalaire
des vecteurs de base ei.ej).
Une métrique Euclidienne peut
toujours être ramenée par changement de variable à la forme caractéristique
ds²= dX1²+ ….+dXi²+..+
dXn²
(
signature +1, Gij =dij)
L'espace de Minkowski est quasi euclidien (
signature +1,-1)
Espaces
Riemanniens ( Variété Riemannienne)
A
partir de la même définition de la métrique
ds²= gμν.dxμ.dxν, les gμν qui sont les éléments
du tenseur métrique ne peuvent pas être ramenés par changement de variable à
une forme Euclidienne et sont des fonctions des
coordonnées.
A noter que pour un point
donné P de coordonnées X0,..,Xn
les gμν ont une valeur définie et que localement on
peut définir un espace Euclidien tangent.
La surface de la sphère est
un espace Riemannien à 2 dimensions. On sait qu'en un point de la sphère on
peut définir un plan tangent ( utile pour faire les
cartes)
Le tenseur métrique
gμν intervenant dans l'élément linéaire différentiel: ds²= gμν.dxμ.dxν
C'est un tenseur de rang (
0,2) donc 0 fois contravariant et deux fois covariant
( forme bilinéaire) dont les éléments dxμ.dxν , peuvent être considérés
comme représentant les vecteurs de base.
Le tenseur métrique est l'élément le
plus important avec l'équation d'Einstein de la Relativité Générale:
Propriétés du tenseur
métrique et de la métrique associée:
Il contient ( intrinsèquement) toutes les informations permettant de
déterminer la courbure ( via la connexion) de l'espace temps ( au moins pour
les variétés Riemanniennes qui nous intéressent)
Il possède également les
propriétés suivantes:
1- Il détermine le passé et le futur
2- Il permet de calculer la longueur d'un chemin et le temps propre
3- Il détermine la plus
courte distance entre deux points, et de ce fait détermine la trajectoire des
particules de test.
4- La métrique remplace le champ gravitationnel Newtonien
5- La métrique fournit la notion de référentiel inertiel et de là également
l'absence de rotation.
6-La métrique détermine la causalité, les trajectoires lumières sont les
plus courtes, aucun autre signal ou point matériel ne
peut aller plus vite.
7- La métrique se substitue au produit scalaire de l'espace Euclidien
de la mécanique classique
8- etc…
Ces propriétés ne sont pas
toutes indépendantes, mais elles mettent en relief le rôle essentiel que joue
la métrique en Relativité Générale.
On sait définir la courbure
d'un tel espace 2D à partir de la différence entre la circonférence d'un cercle
à une distance d'arc "s " d'un point et la valeur" 2.p.s "qu'elle aurait dans
un plan.
Avec r'= a.sin
s/R on déduit s=
arcsin (r'/R) pour la coordonnées
"latitude" l'autre "longitude" qui lui est perpendiculaire
dans le plan tangent vaut r'.dj
![]()
![]()
![]()
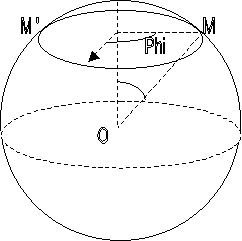
![]()
![]()
![]()
![]()
On arrive à la métrique
suivante : ds² = R²(dr²/(1-kr²) + r².dj²)
La courbure K=1/R², r= r'/R,
R= rayon de la sphère, k= KR²
r' est le rayon du cercle appartenant à la sphère à une
distance s ( dont le centre est dans la troisième dimension)
On montre que cette métrique
est la plus générale et s'applique aux espaces de courbure positive (k=+1),
négative (k=-1) et nulle (k=0)
A noter que cet
espace à 2 dimensions ( et sa métrique associée) est
isotrope ( tous les points de la surface sont équivalent) pas de
"centre" sinon arbitraire. Bien garder ce concept à l'esprit car il va
se conserver pour un espace 3D de type Hypersurface
de l' Hypersphère ( pas de
centre du monde ).
Pendant qu'on est sur l'espace Riemannien
2 D de la sphère profitons en pour examiner quelques problèmes.
-L'expansion de
l'univers, de sa métrique entre 2 points quelconques de cette hypersurface.
cf expansion
- Effet de Courbure:
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()




![]()

![]() Dans un espace de type sphère ,
hypersphère , la courbure de l'espace déforme la
perception ( taille, luminosité ) des objets
Dans un espace de type sphère ,
hypersphère , la courbure de l'espace déforme la
perception ( taille, luminosité ) des objets
Transport parallèle sur un espace courbe
Après
un trajet complet le long du triangle sphérique, le vecteur transporté
parallèlement par rapport aux
coordonnées sphériques a tourné de 90°
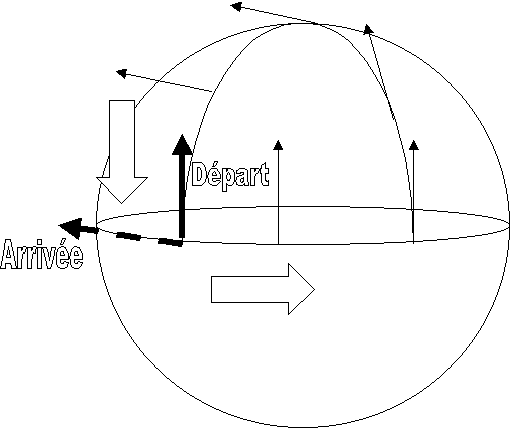
Définition du transport parallèle (cf outils)

Horizon cosmologique dans un
Univers en expansion
Au fur et a mesure que
l'univers vieillit la distance d'horizon des objets visibles croit plus vite ( 3 fois que l'age en cas d'expansion critique , ref 6) que le rayon de l'univers .
Dans une expansion critique , on voit un
pourcentage de plus en plus élevé de l'Univers.
Par contre la surface
d'horizon peut être modulée par la géométrie de l'univers (
dans une hypersphère il croit jusqu'à un
maximum diminue jusqu'à 0 puis varie de façon cyclique).
Il est aussi limité par
l'opacité avant le découplage ( pour la lumière ) et
la date de formation des objets les plus vieux.
A noter que l’intérêt de la
notion d’ horizon pour le RFC, pour la fuite critique
(c) des galaxies.
Renvoi : angles C2,O,X1 = j, O", 0, M = q
![]()
![]()
![]()
Elle se généralise aux
dimensions supérieures (Hypersphère 4D dont l'hypersurface est un espace 3D courbe délimitant un
extérieur et un intérieur (hypervolume) 4D Euclidien.
Cette hypersphère
de rayon R et d'équation x²+y²+z²+w²= R² (1)est
la généralisation de la sphère où l'équivalent des grands cercles de rayon R
sont des grandes sphères de rayon R, l'équivalent des cercles de rayon r sont
des sphères de rayon r, mais qui contient aussi les grands cercles de rayons R
qui sont les géodésiques et tous les autres cercles de rayon r.
La voûte céleste à une
distance s ( mesurée sur l'arc de grand cercle
géodésique) est une de ces sphères contenue dans l'hypersphère.
Au début plus on voit loin et
plus l'horizon augmente ( on verrait de plus en plus
de galaxies si elles sont distribuées régulièrement), il passe par un maximum
pour diminuer, se réduire à 0 avec le fait qu'au antipodes les objets
paraîtraient très lumineux, comme s'ils étaient très proches ( sauf
absorption). Des théories prétendent que les quasars ne sont que des galaxies
ordinaires proches de l'antipode.
On
peut calculer sans problème son hypersurface : 2p².R3, et
son hypervolume: 1/2(p².R4)
Si
l'espace a la structure d'une hypersphère cela a des conséquences originales.
Le
ds² d'un tel espace 3D courbe ,
cf figure ci avant ou calcul analytique en posant:
x² + y² +z² = r² , x= r.sinq.cosj,y=r.sinq.sinj, z=r.cosq et w² = R²- r² dans l'équation (1),
vaut en coordonnées
"sphériques"
ds²= R²(dr²/(1-kr²) + r²( dq²+ sin²q.dj²)) avec k =1
Cette
expression se généralise aux courbures négatives ( k=-1)
et nulle ( k=0).
La
généralisation à l'espace temps conduit à la formule suivante ( on a posé c=1)
ds²= dt²
-R²(t)[(dr²/(1-kr²)
+ r²( dq²+ sin²q.dj²)]
La
contrainte d’homogénéité et d’isotropie de l’espace de l’Univers, conduit à prendre cette métrique pour l’espace dans
l’équation d’Einstein appliquée à la cosmologie.
C'est la formule de
Robertson Walker ( postérieure à l’équation de Friedman)
A noter que l’homogénéité et l’isotropie sont des conditions très contraignantes qui
imposent un degré de symétrie maximum, déterminant la métrique et permettant
une foliation de l’espace/temps par le temps qui apparaît
dans la formule de RW.
On sait définir un temps universel mesuré par exemple par la
température du RFC, ce qui permet de définir des hypersurfaces
3D synchrones. (suite)
Géométrie de la Relativité
Générale : l’approche contemporaine ref 13
<!DOCTYPE
HTML PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN"><!-- saved
from url=(0056)http://cdfinfo.in2p3.fr/Culture/Cosmologie/cosmorg3.html -->Variétés
Si l’espace-temps forme une variété, on dispose d’un "atlas de cartes"
(les coordonnées x ou x) et des "fonctions de transition" x=f(x) d’une carte à l’autre. L’espace tangent T en un
point de la variété définit alors les vecteurs (base ¶/¶xm) ou
tenseurs de type (0,1) qui se transforment comme ¶/¶xm = ¶xm/¶xm ¶/¶xm . Le dual T*
de l’espace tangent définit les formes monolinéaires
(base dxm) ou tenseurs de type (1,0). Les tenseurs de type (p,q) sont définis sur le produit tensoriel (T)pÄ(T*)q
, dont (dxm)pÄ(¶/¶xm)q forment une base (
ƒ dénote
le produit tensoriel).
Les tenseurs définis en un point de la variété n’ont a priori aucun
rapport avec ceux définis en un autre point. En particulier la dérivée
d’un tenseur n’est pas un tenseur (elle n’a pas les bonnes lois de
transformation sous changement de coordonnées).
On
définit alors la dérivée covariante Dm d’un vecteur Vn par :
Dm
Vn = ¶m Vn
+ Gmnr Vr , en
introduisant des connexions Gmnr avec des propriétés de transformation ad hoc
pour que Dm Vn soit un tenseur.
Du
coup, ces connexions ne sont pas elles-mêmes des tenseurs. Avec ces connexions,
on peut comparer des tenseurs pris à des points différents, c’est à dire
transporter un tenseur le long d’un chemin. Le transport est parallèle si la dérivée covariante est
nulle.
Géodésique
Une
géodésique est une courbe transportée parallèlement à elle-même, et elle est
donc la courbe la plus "droite" possible sur une variété. Si une
notion de longueur existe (donc une métrique, mais ce n'est pas une propriété
obligatoire pour une variété en général) la géodésique sera aussi la courbe la
plus courte ( ou la plus longue , en fait un extrémum).
Si
on transporte parallèlement un tenseur d'un point à un autre par deux chemins
différents, on n'obtient pas en général le
même tenseur à l'arrivée. Sur une courbe fermée, un tenseur peut ainsi ne pas
revenir identique à lui-même après transport parallèle.
On dit alors que la
variété possède une courbure, définie mathématiquement par le commutateur des
deux dérivées covariantes :
(Dr Ds - Ds Dr ) Vm = Rmnrs Vn
où = Rmnrs est le tenseur de courbure de
Riemann.
S’il
est nul en tout point, la variété est plate et il existe un système de
coordonnées (les coordonnées cartésiennes!) où les connexions sont nulles en
tout point.
Si
la connexion Gmnr n’est pas symétrique ,
on dit que la variété possède aussi une torsion.
Cartan avait étudié une généralisation de la relativité avec torsion pour
géométriser l'électrodynamique avec la gravité.
Les équations du mouvement étant symétriques, la
torsion ne les modifie pas.
Métrique
L’existence
d’une métrique sur une variété définit la notion de distance. La métrique g est
un tenseur (2,0) de composantes gmn . Un changement
de coordonnées change les composantes de la métrique, mais non sa signature (le
nombre de valeurs propres positives, négatives, ou nulles). Si toutes les
valeurs propres sont positives, on dit que la variété est riemannienne, si
certaines sont négatives, la variété est pseudo -riemannienne ou Lorentzienne comme l’espace-temps. Une métrique permet de
relier vecteurs Vm et formes monolinéaires car les {gmnVm} sont les composantes d’une forme
monolinéaire (notée Vn bien entendu) qui définit le produit scalaire de 2
vecteurs g(V,V’) = gmn
Vm
V’n = Vn
V’n.
La courbe la plus
« courte » possible allant d’un point à un autre est solution de
l’équation "des géodésiques" :
d²xm/ds²+ Gnmr
.(dxn/ds)(dxr/ds) =0
On définit les symboles
de Christoffel: Gnmr = 1/2(glm )( ¶grl/¶xn + ¶gnl/¶xr - ¶gnr/¶xl )
et on
retrouve l’équation de mouvement d’une particule dans un champ de gravitation si on choisit pour connexion les
symboles de Christoffel (qui ont les propriétés de transformations requises).
La courbe la plus courte est alors aussi la plus droite.
La dérivée covariante de la
métrique est automatiquement nulle et le produit scalaire invariant par
transport parallèle.
Courbure
Les
composantes de la métrique dépendent du système de coordonnées, mais il existe
des fonctions de g qui n’en dépendent pas et sont intrinsèques à la variété. A
1 dimension, il n’y en a pas : toutes les variétés sont plates. A 2
dimensions, Gauss a démontré qu’il n’existe qu’une fonction, la courbure
gaussienne K qui permet de classer les variétés : quand la courbure est
constante, cela se limite à l’espace de Gauss-Bolyai-Lobatchevski
(K = - 1/a2) qui n’est pas un sous-espace de l’espace euclidien, au plan (K =
0) et aux sphères (K = 1/a2).
On
ne peut construire aucun tenseur nouveau à partir de g et de ses dérivées
premières (puisque celles-ci s’annulent dans un repère inertiel). Il n’existe qu’un seul
tenseur construit à partir de g et de ses dérivées premières et
secondes qui soit linéaire dans ces dernières (ce qui
est nécessaire pour la physique), le
tenseur de
Riemann : Rnmrs =
¶sGmnr -
¶rGmns + Glnr.Gmsl
- Glns.Gmrl
L’annulation
du tenseur de courbure en tout point est la condition nécessaire et suffisante
pour que l’espace soit plat . Ce tenseur mesure
d’ailleurs la déviation des géodésiques. S’annulant en espace plat, on peut
l’ajouter multipliant n’importe quel tenseur, dans une expression correcte en
l’absence de gravitation, par exemple le mouvement d’une particule libre. C’est
une source d'ambiguïté (quelle est la "bonne" généralisation
gravitationnelle?) dont on se débarrasse en notant que le tenseur de courbure
possède une dérivée de plus que la connexion G, et que les termes où il figure sont a priori d’ordre
devant ceux où figure G.
Par
contraction, le tenseur de Riemann donne le tenseur de Ricci
Rns= Rmnms = ¶lGnls -
Gnlr .Gsrl
puis le scalaire de courbure R = gns Rns. Le tenseur de Riemann possède de nombreuses
symétries. En utilisant la forme complètement covariante Rmnrs = gmlRlnrs on a :
Rmnrs
= Rrsmn, Rmnrs
= - Rnmrs = -
Rmnsr = Rnmsr et Rmnrs
+ Rmsnr + Rmrsn = 0
Les
2 premières impliquent que le tenseur de Ricci est symétrique, et qu’il est
l’unique tenseur de rang 2 que l’on peut construire à partir du tenseur de
Riemann, les 2 dernières que le scalaire de courbure R est unique. En raison de
ces symétries, le tenseur de Riemann n’a que n2(n2-1)/12
composantes indépendantes en n dimensions. A 2 dimensions, la seule composante
indépendante s’exprime donc nécessairement en fonction du scalaire R. De fait, Rmnrs = R [gμρgνσ-gμσgνρ]/2 . En 3 dimensions, il y a 6 composantes indépendantes
que l’on peut exprimer en fonction des 6 composantes indépendantes du tenseur
de Ricci. En 4 dimensions, il y a 20 composantes indépendantes, les 10
composantes du tenseur de Ricci ne suffisent plus à absorber l’information, et
le reliquat définit le tenseur de Weyl (symboliquement, Riemann = R*g*g +
Ricci*g + Weyl).Ce n’est pas tout
Le tenseur de Riemann
étant le commutateur de 2 dérivées covariantes, sa dérivée covariante Di
est nulle. Plus exactement on obtient l’identité
de Bianchi :
Dδ
Rmnrs
+ Dσ Rmnδr + DρRmnsδ = 0
Celle-ci
joue un rôle essentiel dans la théorie de la relativité générale. Par
contraction, elle devient :
Dμ [ Rμν - gμν .R/2 ] = 0
ce qui suggère directement la forme des équations
d'Einstein de la gravitation :
Rμν-gμν.R/2= - 8p.G.Tμν , en
présence de matière,car DμTμν = 0
(conservation de l'énergie-impulsion). Plus
profondément, l'identité de Bianchi est reliée à
l'invariance des équations par changement de coordonnées.
Espaces symétriques
On
s’intéresse souvent à des espaces-temps possédant certaines symétries
(sphériques pour Schwarzschild, espace homogène et
isotrope pour Friedmann…). Dans un changement de coordonnées x ®
x’, la métrique se transforme suivant
gμν(x) = (¶x'r/¶xm )(¶x's/¶xn ).g’ρσ(x’) .
Si
sa forme fonctionnelle ne change pas, c’est à dire que g’ρσ(x’) = gρσ(x)
pour tout x, on dit qu’on a une isométrie. Pour une transformation
infinitésimale x’ = x + ex, cela se traduit par Dmxn
+ Dnxm = 0 (équation
de Killing).
Inversement,
il existe des isométries s’il existe des solutions de l’équation de Killing (les vecteurs de Killing xm). On montre que sur une variété de
dimension n il existe n(n+1)/2 isométries au maximum.
Si
la variété est isotrope en un point, on peut permuter tous les vecteurs de base
de l’espace tangent en ce point : en dimension n, il y a n(n-1)/2
permutations (qui sont des isométries). Le tenseur de Riemann prend
alors une forme particulièrement simple : Rmnrs
= K(gμρgνσ-gμσgνρ ) .
La
courbure gaussienne K peut varier d’un point à un autre, tout comme gmn. Si K º 0 (espace plat), les isométries sont des rotations (espace euclidien)
ou des transformations de Lorentz (espace de Minkowski).
Si
la variété est homogène, il existe des isométries transportant la métrique d’un
point à un autre : en dimension n, il y a n vecteurs de Killing
correspondants. Si l’espace est plat, ces isométries sont de simples
translations. Si la variété est homogène et isotrope, on totalise n(n+1)/2 isométries, la symétrie est maximale et K
est constant sur la variété. Dans ce cas, le tenseur de Ricci s’écrit Rmn
= K(n-1)gmn et le scalaire
R = Kn(n-1). La
valeur de n et de K (et la signature de la métrique) déterminent
entièrement la métrique.
Mais,
en général, on ne souhaite pas que l’espace-temps soit maximalement symétrique,
mais seulement qu’un sous-espace le soit. Séparons les coordonnées xm en {ui,va},
où les indices i = 1…m décrivent ce sous-espace, et
les indices a = m+1…n les dimensions complémentaires.
On
démontre alors que la métrique peut s’écrire sous la forme ds² = gab(v)
dvadvb + f(v) gij(u) duiduj, où la métrique gij a la forme déterminée par
la symétrie du sous-espace, qui dans tous les cas physiques est un espace (par
opposition à un espace-temps).
Par
exemple, pour un espace-temps à 4 dimensions possédant un sous-espace à 2
dimensions de symétrie sphérique, il y a 2 coordonnées v (appelées en général t
et r) et 2 coordonnées u (qui sont sinq.cosj
et sinqsinj).
Pour une courbure K positive, la métrique du
sous-espace est : dij +( Kuiuj./1-
Kuiuj.)
La
forme générale du ds² est alors :
ds² = gtt(t,r).
dt² + 2 gtr(t,r). dt.dr
+ grr(t,r). dr² - f(t,r) ( dq² + sin²q .dj² )
où gab(t,r) est une matrice 2
x 2 avec une valeur propre positive et une négative, et f(t,r) une fonction quelconque positive.
Par
changement de variable, on peut la ramener à la forme :
ds²
= A(t,r) dt² - B(t,r) dr² - r² ( dq² + sin²q
.dj² )
Cette
forme du ds² permet de calculer la métrique statique de Schwarzschild autour d’une masse ponctuelle. Elle sert
aussi à calculer la métrique autour d’une distribution de masse variable mais
sphérique.
En
dehors de cette distribution, on retrouve d’ailleurs la métrique statique de Schwarzschild (théorème de Birkhoff, analogue au théorème
de Newton qui permet de calculer le champ d’une distribution sphérique comme si
toute la masse était concentrée au centre).
Si le sous-espace de symétrie maximale est l’espace à 3 dimensions
lui-même, il n’y a qu’une coordonnée v et 3 coordonnées u (vecteur u), et le ds²
prend la forme :
ds² = g(v) dv² -
f(v)[ du² + K (u.du)²/1-Ku²)]
où f et g sont des fonctions positives de v. La forme
classique de Robertson et Walker est obtenue par un
astucieux changement de variables t = òdv/Ög(v) , u1 = r sinq cosj, u2
= r sinq sinj et u3 = r cosq :
ds² = dt² - a²(t) [(
dr²/1-kr²) +r² ( dq² +
sin²q.dj²)]
La
fonction arbitraire a(t)Öf(v) s’appelle le
paramètre d’échelle , et le paramètre k ne
prend que les valeurs 1, 0 ou -1. La courbure spatiale K3 = k/a2(t)
s’annule pour k = 0, mais pas la
courbure spatio-temporelle K4 = (k+2)/2a2 .
L’intérêt
de ces divers métriques est qu’elles ne reposent que
sur des hypothèses d’homogénéité et d’isotropie de l’espace, et sont totalement
indépendantes des équations d’Einstein de la gravitation. Elles restent donc
valables dans d’autres théories métriques de la gravitation que la relativité
générale.
Variété : C’est
un des concepts fondamentaux de la physique et des mathématiques.
La
notion de Variété procède de l’idée que l’espace peut être courbe et avoir une
topologie complexe, mais que localement , il peut être
assimilé à l’espace Euclien, caractérisé par ses n-tuples Rn
Vecteurs de Killing :
Champ de vecteurs sur la
variété qui caractérisent les isométries de la variété.Pour la métrique, ils
caractérisent son invariance par transformation par ce champ de vecteurs.
Ils impliquent la
conservation de quantités comme l’impulsion sur les géodésiques de particules
en mouvement « libre ».. Le vecteur tangent
à la géodésique est un vecteur de Killing.
Un espace de symétrie maximum
est celui qui contient le maximum de vecteurs de Killing
=< n(n+1)/2
8-Outils : Tenseurs, Calcul tensoriel
Quelques définitions.
Composantes contravariantes d'un vecteur X
(1) X= xi.ei , ( i de 0 à n-1) xi composantes
contravariantes, les ei
sont les vecteurs de la base de l’espace vectoriel En
Ces composantes sont les composantes
"habituelles" d'un vecteur, dans n'importe quel système de
coordonnées.
Sur un espace Vectoriel de dimension n, à partir d'une
"n" base et de n scalaires ( nombres) on construit un être
mathématique appelé vecteur d’un espace à n dimensions, qu'on représente comme
une « flèche » avec une origine s'il est lié.
Composantes covariantes d'un
vecteur X
xj=X.ej ( produit scalaire), xj composantes
covariantes.
En substituant à X sa valeur
dans (1) et en utilisant les propriété des déterminants et du fait que gij =ei.ej , on tire les relations
suivantes entre les composantes contra et covariantes qui sont utilisées en RG:
xi=gij.xj
xj=gij.xi
A noter que dans une base cartésienne orthonormée d'un
espace Euclidien, les composantes contra et
covariantes coïncident
De
façon plus mathématique, à partir d'un espace vectoriel qui contient les
vecteurs et leurs composantes contravariantes on sait
définir l' espace dual (qui a même structure) des
formes linéaires appliqué aux composantes de ces vecteurs. Le dual du dual est
l'original
Coordonnées curvilignes
Sur un espace ponctuel
Euclidien En ( éléments sont des points)
sur lequel est défini un repère (point O + une base e1,…,en)
si M appartient à En, OM= xi.ei
Si xi s'exprime en fonction
de n variables yi, par :
xi=fi (y1,y2,…yn), Les yi sont les coordonnées
curvilignes.
Si
un seul yi varie on obtient la courbe « coordonnée
yi »
Exemple
représentation du plan en coordonnées polaires et cartésiennes: X = r.cosq, Y= r.sinq
La
droite représentée X=cte s'écrit r.cosq = Cte soit r= Cte/cosq, ce qui n'est pas du tout linéaire
![]()
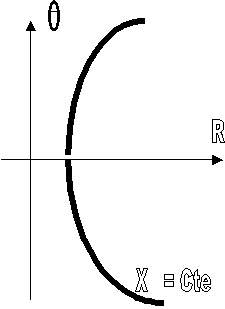
Repère naturel en M
Vecteurs
tangents aux courbes en M vecteurs base (ei)
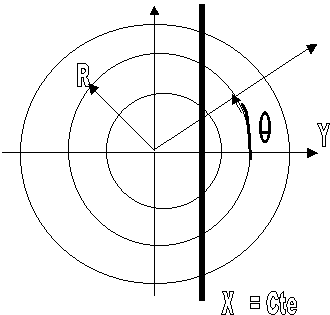
Changement de repère
en M (Changement de Coordonnées)
ê'j=Aij.êi
avec Aij = ¶yi/¶y'j
Elément linéaire de
l'espace
x.y= Gij.xi.xj avec Gij
= êi.êj
Problème
fondamental de l’analyse tensorielle
Connexion
métrique
En coordonnées curvilignes à
partir du repère naturel défini en M, elle définit comment déterminer le repère
naturel au point infiniment voisin M'
C'est un concept fondamental de l'analyse
tensorielle, la variation du repère,
variation des vecteurs de la base tangente au coordonnées
curvilignes va dépendre de la dérivée des Gij.
Par définition ei= dM/dyi
dei/dyk=d²M/dyi.dyk , dei est une combinaison linéaire des dy il vient :
(2) dei= Gkji.dyk.ej
Gkji. est le
symbole de Christoffel qui est symétrique en indices bas si la torsion est
nulle et qui n'est pas un tenseur mais
dont la différence est un tenseur
Sachant que ei.ej=Gij
en différentiant cette expression et en remplaçant dei par sa valeur définie
dans (2) au bout d'un calcul un peu laborieux il vient
(3) Gkji=1/2(¶Gij/¶Xk + ¶Gjk/¶Xi - ¶Gki/¶Xj) Symbole de
Christoffel de 1 ère espèce.
Celui de 2 ème espèce ( le plus utilisé) s'obtient par multiplication Gkhj par Gih.
(4)
Gikj = 1/2(Glk )( ¶Gjl/¶xi + ¶Gil/¶xj - ¶Gij/¶xl
)
Dérivée covariante
d'un vecteur
A la dérivée du vecteur ( covariant dans cet exemple) il faut soustraire ( ajouter
si contravariant) le
changement d'orientation qui est du à l'espace (courbe) (cf transport // d'un vecteur ci
dessous)
DVi/Ds=dVi/ds - Gjki.Vj.dxk/ds
Transport
parallèle d'un vecteur
En
coordonnées curvilignes le transport // d'un vecteur s'obtient en déplaçant le
vecteur de façon à conserver l'angle qu'il fait localement avec la courbe ( la tangente à la courbe).
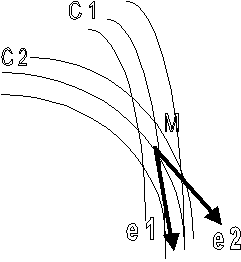
![]()
![]()
On
voit que si on situe ces coordonnées curvilignes dans un espace Euclidien
cadre, la direction dans cet espace change ( elle suit
la courbe)
C'est
pour cela que la dérivée covariante d'un vecteur s'obtient en calculant
localement la variation du vecteur et en retranchant la part de variation due à
la courbure de "l'espace" , c.a.d à la courbe
Equation Géodésique cf ref 4 & 2
Méthode
1 ( Géométrique la plus
simple)
Partant du fait que la
géodésique est une droite en RR on effectue le changement de coordonnées pour
trouver son équivalent dans un système quelconque. Cette méthode est la plus
immédiate mais le résultat ne met pas directement en évidence que cette
équation ne dépend que de la métrique du système quelconque. On va chercher une
autre méthode qui relate l'équation géodésique uniquement en termes de métrique
de l'espace temps concerné.
Méthode
2 ( Méthode « physique » originale
d’Einstein)
On
écrit que la géodésique est la courbe qui minimise l'intégrale du chemin (ds).
En
fait Einstein utilise sans le dire, le Lagrangien : L(x,dx/dp) = ½(gμν).
(dxμ/dp) (dxν/dp) qui est L= ½(ds²/dp²) qui correspond à
l’intervalle d’espace temps,
En
appliquant l'équation d'Euler Lagrange du mouvement qui exprime la condition
d’extremum: d/dp(¶L/¶(dxμ/dp)) = ¶L/¶xμ, On
arrive à: d²Xs/ds²+ Gmsn
.(dXm/ds)(dXn/ds) = 0
Rappellons que l'équation du mouvement ( géodésique) est contenue dans l'équation du champ.
Remarquons la
similitude avec l'équation du mouvement de Newton, (Courbure = Force)
Rappel:
Fonction de Lagrange du mouvement ( Lagrangien)
en mécanique classique
L (x,y,z,x',y',z',t) = ½. m ( x'²+y'²+z'² ) -
U (x,y,z,t ) = W-U avec W énergie cinétique
L'équation du mouvement
exprime que son intégrale òt0t1 L.dt ( intégrale d’action Hamiltonnienne)
est minimum sur la trajectoire réelle ce
qui implique:
d/dt(¶L/¶x') - ¶L/¶x
=0 ( idem en y et z)
Fonction de Hamilton en mécanique classique(pm)
H (x,y,z,x',y',z',t) = ½. m ( x'²+y'²+z'² ) + U (x,y,z ) = E « énergie totale »
Association d’un opérateur à
une grandeur physique pour généraliser l’équation classique à la mécanique
quantique par application sur la fonction d’onde y.
à E ( énergie) on associe i(h/2p).¶/¶t
à px = m x’ (quantité de mouvement ) on
associe (h/2pi)¶/¶x ( idem pour y,z)
Tenseurs
Scalaires
En établissant
l’expression de l’intervalle ds², dans un référentiel
arbitraire {Xi}, on a implicitement postulé l’invariance de la
valeur numérique du ds², lors d’un changement de
référentiel ( X’j au lieu de Xi).
L’intervalle ds² est un scalaire, c.a.d la donnée en chaque point de l’espace temps d’un nombre
indépendant du choix d’un référentiel particulier . Un
scalaire est un tenseur de rang 0. De façon générale on appelle scalaire tout
champ S(x) tel que dans un changement arbitraire de référentiel produisant S’
(x’) on ait : S(x) = S’
(x’)
Il faut bien distinguer cette notion de scalaire d’avec le
postulat de Relativité qui implique que non seulement la valeur numérique de
l’intervalle, mais surtout sa forme est la même dans tous les référentiels
inertiels.
Quadrivecteur contravariant
On suppose connu la notion de
vecteur défini dans un espace vectoriel , ensemble dont les éléments sont les
vecteurs muni d'une relation d'égalité, d'une
loi interne d'addition commutative, associative munie d'un élément
neutre et d'un inverse et d'une loi externe de multiplication par R, corps de
réels ( distributive,...).
Le qualificatif contravariant vient de ce que, lors d'un changement de base
les coordonnées (xi) varient selon la transformation inverse de celle des
vecteurs de la base (ei).
En physique, un champ de
(quadri)vecteurs a un caractère intrinsèque qui peut
être défini indépendamment du
référentiel ( exemple quadri vitesse Ui = dXi/dt avec dt invariant car
dt = ds²/c²).
Cas particulier: Un élément
linéaire est défini par ses 4 composantes dXi dont l'équation: dX'j=(¶X'j/¶Xi).dXi
exprime la loi de transformation linéaire et homogène .
Pour cette raison, on
considère les dXi
comme les composantes d'un quadrivecteur (tenseur de rang 1 )
qu'on appelle contravariant.
Tout objet défini par rapport
au système de coordonnées ( base d’un espace vectoriel
de dimension 4 dans ce cas) par 4 grandeurs Ai et qui se transforme
selon la loi:
Ai'= (¶X'i/¶Xj).Aj est aussi appelé quadrivecteur (
tenseur de rang 1) contravariant
Quadrivecteur
covariant
Si on définit l'ensemble des
formes linéaires fi(Vj)
telles que fi (Vj + Vk) = fi (Vj)+
fi (Vk) et fi(a.Vj) = a. fi(Vj) sur les vecteurs contravariants
de l'espace vectoriel associé aux vecteurs contravariants
, cet ensemble a également une structure d'espace vectoriel.
Il est appelé espace dual du
premier. Il contient les vecteurs covariants.
Le qualificatif de covariant
vient du fait que lors d'un changement de base, les composantes se transforment
comme les composantes des vecteurs de base, ceci implique alors.
Un ensemble de 4 grandeurs Ai
est appelé quadrivecteur covariant si pour n'importe quel choix
de vecteurs contravariants Bj
on a :
Ai.Bi= invariant ( par changement de
coordonnées).
On
en déduit la relation: A'i= (¶Xj/¶X'i).Aj
A noter la dualité entre
l’espace vectoriel des vecteurs contravariants et
covariants ( si l’un est un espace vectoriel de
référence, l’autre est l’espace vectoriel, dual, des formes linéaires sur ce
premier et vice versa, le dual du dual est l’original). Les vecteurs de base de
ces espaces vectoriels dont les grandeurs Ai représentent les composantes sont
notés respectivement ei et e*j.
Tenseur contravariant
Exemple tenseur de rang 2 : Notion de tenseur ( produit
tensoriel).
On forme les 16 produits Aij des composantes Ai et Bj de 2 quadrivecteurs contravariants:
Aij= Ai.Bj
On appelle cette
opération "produit tensoriel", les 16 composantes ainsi produites
sont les composantes du tenseur Aij , à noter que le tenseur résultant a ses
composantes i dans l'espace vectoriel associé au vecteur Ai et ses composantes j dans l'espace
vectoriel associé au vecteur Bj
Des propriétés des vecteurs on déduit: Aij'=(¶X'i/¶Xk)(¶X'j/¶Xl).Akl
Par extension, on
appelle tenseur contravariant de rang 2 tout objet de
composantes Akl qui satisfait
la relation ci dessus
C’est la définition fondamentale d’un
tenseur contravariant
A noter que ceci implique la notion de produit d’espaces
vectoriels, puisque le tenseur est
défini dans l’espace produit qui contient la « base »( qui correspond à ses composantes) .
Tenseur covariant
De
même, on appelle tenseur covariant d'ordre 2 un objet de composantes Aij qui satisfait la relation
A'kl=(¶Xi/¶X'k)(¶Xj/¶X'l)Aij
C’est la définition fondamentale d’un
tenseur covariant
Un tenseur covariant
d'ordre 2 prend un tenseur contravariant d'ordre 2 ( ou 2
vecteurs contravariants) en entrée et produit un
scalaire en sortie .Cela se généralise aux ordres supérieurs
A noter que ceci implique notion de produit d’espaces vectoriels duals dans lequel est défini le tenseur (ses composantes).
Le produit d’un
tenseur contravariant ( ou
de n vecteurs contravariants) par un tenseur covariant de même rang et
dimension produit un scalaire , c’est à dire quelque chose d’invariant par
rapport aux coordonnées.
Si
Tij se transforme en T’ij par changement de coordonnées xk en x’k
Si Tij
se transforme en T’ij par le même
changement de coordonnées xk en xk’
Alors Tij
.Tij = T’ij
.T’ij Ce qui exprime
l’invariance ! ! ! !
Tenseur mixte et de rang supérieur
à 2
C'est le tenseur de plus
général qui possède des composantes contravariantes
et covariantes dont les tenseurs présentés précédemment ne sont de des cas
particuliers.
La
loi à laquelle il obéit est évidente ( extension et
combinaison des lois précédentes)
A noter que ceci implique notion de produit mixte d’espaces
vectoriels et d’espaces vectoriels duals dans lequel est défini le tenseur (ses
composantes).
Une
autre présentation rigoureusement équivalente et plus "intuitive" est
la suivante cf ref
7
Un tenseur Tj,k ,
noté de rang (j,k), j fois contravariant et k fois covariant prend en entrée j
vecteurs covariants et k vecteurs contravariants et
génère un nombre. Ce nombre en sortie est une fonction linéaire des entrées.
Une autre manière est de
dire qu'il prend en entrée k vecteurs contravariants
et produit en sortie j vecteurs contravariants, ce
qui est équivalent car si on rajoute en entrée les j vecteurs covariants ils
"mangent "les j vecteurs contravariants
pour produire un nombre!!
Cette définition correspond à
la construction d’un tenseur ( l’autre à ses
propriétés).Cf ref
4
Exemples : le tenseur métrique Gij est un tenseur covariant de rang 2 et de dimension
4. Le tenseur métrique inverse Gij est un
tenseur contravariant de rang 2 et de dimension 4
Quelques
opérations utiles sur les tenseurs
On peut additionner ( soustraire)
des combinaisons linéaires de deux tenseurs de même nature, n fois contravariant et p fois covariants avec même dimension
d’indice.
On
peut multiplier des tenseurs par un scalaire
Multiplier de
façon externe deux tenseurs: T ijk = Aij.Bk par exemple ( on
multiplie deux à deux toutes les composantes du premier par toutes celles du second)
Le rang est la somme des
rangs
Contracter les tenseurs ( sommer sur un indice haut et bas ) Contraction de Rjikl
On fait i=k et on somme Rjiil
= Rjl
Elever /abaisser les indices à l’aide du tenseur métrique ou du
tenseur métrique inverse en particulier par exemple Rjikl
. Gih = Rjklh ,
à noter que les composantes du tenseur métrique inverse sont les cofacteurs de
celles du déterminant du tenseur métrique d’ou Gij.Gij = dii
= 4
Jacobien d’une transformation.
Il est parfois utile d’opérer des transformations sur
des objets non tensoriels. Un exemple important est le déterminant du tenseur
métrique G = det Gij,
qui se transforme en G’ tel que G’ =[det(¶x’i/¶xi)]-2.
G. Le facteur « det(¶x’i/¶xi) » est
le Jacobien.
Densité de
tenseur
Des objets avec une telle loi
de transformation ( impliquant des puissance du Jacobien) sont appelés
densité de tenseur
Un
autre exemple de densité de tenseur est le volume d4x
= dx0dx1dx2dx3
d4x’ =[det(¶x’i/¶xi)].
d4x . On peut définir un élément de volume
invariant
d4x
.(-G)1/2 qui
neutralise le facteur Jacobien.
Dérivée covariante
d'un tenseur
La dérivée classique d’un
tenseur n’étant pas un tenseur, pour conserver ce caractère tensoriel il faut
apporter un terme correctif et définir
par là une dérivée covariante.
A partir d'un tenseur
covariant de rang 1, Ai= dF/dxi,
on peut former par dérivation un tenseur covariant de
rang 2
Aij=
dAi/dXj - Gikj.Ak
Le
tenseur Aij est appelé extension de Ai
En fait pour un vecteur (
tenseur(0,1)) la dérivée covariante corrige la variation intrinsèque propre à
la courbure de la courbe sur laquelle on
opère la dérivation, et rend ainsi
compte uniquement de la variation relative du tenseur par rapport a la courbe.
Divergence covariante
d'un vecteur
Divergence de Vi,i = dVi/dxi + GiijVj
Divergence covariante d'un tenseur
Divergence de Tij = dTij/dXi + GiikTkj
+ GjlkTlk
Tenseurs
particulièrement utilisés en Relativité Générale
Tenseur de Riemann Cf Ref 8 & 2&4
Einstein a
cherché comment construire un tenseur ne contenant que les dérivées premières
et secondes des éléments du tenseur
métrique pour construire dans le domaine
tensoriel covariant l'équivalent de l'équation de Poisson. Il est tombé sur le
tenseur de Riemann ( solution unique ).
Ce tenseur
s'établit indépendamment , de façon théorique en faisant parcourir dans un système de coordonnées
curvilignes un parallélogramme infinitésimal et en comparant les orientations
de départ et d'arrivée d'un vecteur transporté parallèlement sur la courbe.

![]()
La différence traduit la
courbure et s'exprime par un tenseur assez compliqué: le tenseur de Riemann
mixte du 4éme ordre ( 3 fois covariant et une fois contravariant ) dont les éléments sont les dérivées
premières et secondes des éléments de la métrique.
A noter que cette courbure
est une quantité du deuxième ordre.
ddEi
- ddEi = Ej.Rijkl.dYk.dYl
L'espace
est supposé sans torsion (
le parallélogramme curviligne est fermé ).
Ce tenseur fondamental décrit complètement
la Courbure intrinsèque de l'espace temps au point considéré, mesurable
par des observateurs confinés dans cet l'espace. (
généralisation à N dimensions de la Courbure de Gauss ). Ne
pas confondre avec la courbure extrinsèque que pourrait avoir l'espace, s'il
était plongé dans un espace de dimensions supérieures et qui serait mesuré par
des observateurs vivant dans cet espace.
Tenseur de Riemann : Rnmrs = ¶sGmnr - ¶rGmns
+ Glnr.Gmsl
- Glns.Gmrl
Quelque chose de compliqué à calculer, combinaison de différences de dérivées de
Symboles de Christoffel et de différence de produits de ces symboles.
Ce tenseur possède de
nombreuses symétries ( 20 composantes différentes pour
256 possibilités) et décrit exhaustivement la
courbure locale de l'espace.
Si par un choix de coordonnées , les éléments du tenseur métrique sont
localement constants à un point P, (référentiel chute libre correspondant à un
espace tangent de Minkowski), alors le tenseur de Riemann est localement nul au
point P ( la dérivée première du tenseur métrique=0)
Et s'il est nul dans un référentiel
donné, il l'est dans tous, propriété fondamentale de la RG
En revenant à la définition intuitive des
tenseurs, le tenseur mixte de Riemann, 3 fois covariant et 1 fois contravariant ,
va prendre en entrée 3 vecteurs contravariants U,V,W
et produire en sortie un vecteur contravariant W' qui
est issu du transport de W le long du parallélogramme curviligne infinitésimal
défini par U,V , Cf ref 7
R(U,V,W)μ = Rνμρσ.Uν,Vρ,Wσ
Le
tenseur de Riemann possède de nombreuses (anti)symétries.
En utilisant la forme complètement covariante Rmnrs = gmlRlnrs on a :
Rmnrs
= Rrsmn, Rmnrs
= - Rnmrs = -
Rmnsr = Rnmsr et Rmnrs
+ Rmsnr + Rmrsn = 0
Ce
n’est pas tout : le tenseur de Riemann étant le commutateur de 2 dérivées covariantes,
sa dérivée covariante Di est nulle. Plus exactement on obtient l’identité
de Bianchi :
Dδ
Rmnrs
+ Dσ Rmnδr + DρRmnsδ = 0
Celle-ci
joue un rôle essentiel dans la théorie de la relativité générale. Par
contraction, elle devient :
Ou
on trouve les tenseurs et scalaire de RICCI
Cette forme suggère
directement le tenseur d’Einstein ( Seul tenseur
construit à partir des dérivées premières et seconde du tenseur métrique et à
divergence nulle )
Tenseur de
Ricci : cf ref 2
Par contraction de deux
indices on obtient le tenseur covariant d'ordre 2 de Ricci: Rij ( 10
composantes qui permettent de reconstituer 10 composantes du tenseur de
Riemann)
Ce
tenseur rend compte au deuxième ordre de la variation de volume dans son
parcours sur les géodésiques.
Rns= Rmnms = ¶lGnls -
Gnlr .Gsrl
Mais
où sont passées les 10 autres
composantes ?
Bonne question: D'abord on ne
peut pas annuler complètement le tenseur de Riemann, ce qui voudrait dire que
par un changement de référentiel on compenserait un champ de gravitation (on ne
le fait que très localement).
Par ailleurs le tenseur
Impulsion Energie ne contient pas toutes les informations au sujet de la courbure , le tenseur
de Weyl = Wabcd
contenant le complément lié à la courbure propre de l'espace.
si le
choix des coordonnées est tel que (-g) -1/2 = 1 avec g
"déterminant du tenseur métrique.
Le tenseur de Ricci (
Cf ref 7 )contrôle la
dérivée seconde du changement de volume, d'un petit volume lors de sa
trajectoire géodésique.
d²V/dXa,dXb= RA,b .Va.Vb
Le tenseur de Weyl
contrôle la déformation ( sphère/ellipsoïde)
C'est le tenseur de Ricci qui
figure dans l'équation, car la distribution de matière /énergie ne définit pas
complètement le tenseur de Riemann.
Scalaire de Ricci
On
l'appelle scalaire de courbure
Par
multiplication du tenseur de Ricci par gnsj
on obtient le scalaire de Ricci : R = gns Rns.
Ce scalaire qui résulte de contractions multiples du tenseur de
Riemann en synthétise les informations essentielles et est à ce titre très
important ( cf principe de moindre action)
Tenseur
d'Einstein
C'est
une combinaison du tenseur de Ricci, du scalaire de Ricci et du tenseur
métrique
Gμν=
Rμν-
1/2.(gμν.R)
Ce
tenseur est symétrique et à divergence
nulle par construction :cf
Identité
de Bianchi
Le tenseur d’Einstein qui va être utilisé dans l’équation de la
gravitation ne définit pas complètement la courbure de l’espace puisque alors
que le tenseur de Riemann a 20 composantes , le
tenseur symétrique d’Einstein n’en n’a que 10.
La
signification profonde est que le tenseur énergie Impulsion, qui décrit la
répartition de matière énergie, auquel le tenseur d’Einstein va être égalé ne
contrôle que 10 paramètres de cette courbure ( mais
pas n’importe lesquels cf tenseur de Ricci).
Les
autres paramètres sont « extérieurs « à l’équation de la gravitation
et apparaissent comme des degrés de liberté vis à vis de la solution.
Il
dépendent, par exemple de la métrique ( l’équation
d’Einstein est valable pour n’importe quelle métrique) ou de conditions
initiales, aux limites.
Tenseur
Impulsion Energie : Cf ref 7
Tij: Il traduit le flux d'énergie sous
toutes ses formes, au point P. Tij
correspond au flux de densité d'impulsion dans la direction xi s'écoulant dans
la direction xj.
Il s'agit de l'Impulsion relativiste ( quadrivecteur dont les composantes sont: E/c pour X0
(temps), et : m.V1 pour X1,m.V2 pour X2,m.V3 pour X3 , dimensions x,y,z
d'espace)
Pour la coordonnée 0 ( le temps ) cela s'interprète comme suit:
T00 : Densité d'énergie, car
Energie = Impulsion dans la direction du temps
et densité = flux dans la direction du temps
T01,T02,T03
: densité d'Impulsion dans les directions x, y, z,
T10,T20,T30
: flux d'énergie dans les directions x,y,z
Autres Tij
relatent le flux d'Impulsion de direction i dans la direction j
Ce tenseur est symétrique et
à divergence nulle, c'est pour cela que le tenseur d'Einstein doit avoir ces
propriétés.
Il
ne contient pas toutes les informations au sujet du tenseur de Riemann
Pour le modèle cosmologique ( Univers FLRW) on simplifie ( Cf ref 4), l'énergie étant assimilée à un fluide parfait
sans viscosité de densité d et de pression p dont le tenseur associé est : Tμν= ( p+r)uμ.uν
- p. gμν
9-Les Résultats
Equation
géodésique
Retour sur l'équation
de la gravitation d'Einstein
Rμν-1/2[gμν(R-2L)]=0 en
l'absence de matière ( mais pas de champ)
Rμν-1/2[gμν(R-2L)]= - 8pGTμν en présence de
matière
Einstein a obtenu cette
équation par " généralisation
"de l'équation de Poisson qui relie les dérivées secondes du potentiel
gravitationnel Newtonien à la densité
de masse gravitationnelle à partir des hypothèse suivantes: Cf ref 1
La généralisation relativiste
de r (
densité de matière ) est de façon unique le Tenseur Energie Impulsion à
cause des équivalences masse gravitationnelle = masse inertielle = énergie / c²
et de l'absence en RR de description par un scalaire ou un vecteur de la
distribution d'énergie.
Alors comme le choix du
référentiel est arbitraire Einstein s'est posé le problème de trouver un tenseur Sij
formé à partir du tenseur métrique et de ses dérivées premières et secondes qui
puisse être égalé au Tenseur énergie Impulsion ( à une constante d'ajustement
de dimension près)
Exigence de covariance
pour conserver la même forme par changement de coordonnées.
L'énergie est décrite par le membre de
droite par un tenseur à divergence nulle ( flux
conservatif ), donc la partie gauche de l'équation doit donc satisfaire
également à l'exigence de divergence nulle.
Ce doit être un tenseur
complètement déterminé par le tenseur métrique et ses dérivées
premières et secondes ( analogie avec
l’équation de Poisson : part d'arbitraire limitée)
-
à
noter que si on admet la présence de dérivées d'ordre supérieur à 2, il est
possible de trouver un tenseur avec beaucoup de constantes arbitraires
, faisant intervenir des termes non linéaires du tenseur de Riemann. Il
n'existe pas pour l'instant, de faits expérimentaux suggérant une telle
généralisation, mais les tentatives de quantification de la gravitation et son
unification prévoient de telles modifications aux courtes distances)
La limite en l'absence
de matière doit être la métrique de Minkowski
Hypothèse à été remise en
cause pour permettre l'introduction de la constante cosmologique.
Limite de Newton pour
champ faible , stationnaire et vitesse faibles (
équation de Poisson)
Il y a une solution
unique qui est le tenseur d'Einstein (cf identité de Bianchi).
En
effet, le tenseur de Riemann est trop contraignant ( 20
composantes indépendantes), car le tenseur énergie impulsion n'en comporte que
10.
Notons pourtant que la courbure de l'espace est
déterminée complètement par le tenseur de Riemann, qui est complètement
déterminé par la métrique (dont ses dérivées premières et secondes).
Lorsqu'on
à choisi la métrique, le tenseur de Riemann est donc
connu, on peut se demander à quoi sert alors l'équation de la gravitation,
sachant qu'elle s'applique à n'importe quelle métrique.
En
fait la plupart du temps la forme de la
métrique, correspondante à une situation particulière peut être déterminée,
indépendamment de l'équation, par des considérations de symétrie.
Les
éléments de l'équation de la gravitation ( tenseur de
Ricci, scalaire de Ricci qui sont dérivés du tenseur de Riemann) et
éventuellement les contraintes associées par l'équation permettent de
déterminer des paramètres non définis ( 10 équations , en fait 6 indépendantes:
identité Bianchi). Les autres peuvent l'être par des
conditions aux limites. L' équation permet de décrire
les relations entre les variables sous forme d'un
ensemble d'équations différentielles.
Les
autres paramètres de courbure ( 10) non explicitement
contenus dans l'équation, et pas contenus dans le tenseur ni le scalaire de
Ricci, sont implicitement contenus dans la métrique et explicitement dans le
tenseur de Weyl " l'autre partie du Tenseur de Riemann"
L'exemple
typique est l'application à la Cosmologie.
A
noter la complétude des
équations du champ. Elles contiennent les équations du mouvement de la
matière ( comme conséquence de la conservation de
l'énergie ÑmTmn ) à la différence de l’électromagnétisme ( force de
Lorentz postulée indépendamment des équations de Maxwell) ainsi que les champs
centrifuge ou de Coriolis ( ¹ Newton)
Ces
équations différentielles sont en général complexes à
résoudre ( solutions pour des métriques présentant des
symétries importantes) et sont non linéaires.
En
particulier la masse grave de deux masses en interaction
gravitationnelle n'est pas la somme des
masses graves individuelles pour
respecter le principe d’équivalence mg=mi.
Le champ gravitationnel se couple avec
lui même pour compenser ce défaut . Ayant une énergie,
il « gravite ».
C’est
pourquoi il est possible d’avoir des champs de gravitation qui sont leur propre source dans un espace vide et donc des
modèles d’Univers courbés sous l’effet de l’énergie
de gravitation résultant de leur courbure et vide de toute matière! ! !.
L’équation de la gravitation
qui n’annule que les 10 composantes du tenseur de Ricci quant le tenseur
Energie Impulsion est nul, n’annule pas le tenseur de courbure de Riemann
qui a 20 composantes, permet de telles solutions ( courbure
sans matière)
A noter que aujourd’hui on déduit l’équation
« d’Einstein » de la condition extrémale d’intégrale d’un Lagrangien
La métrique
associée à cette équation a une solution exacte dans le cas de masse à
répartition centrale (à l'extérieur de la masse) :
La métrique de Schwarzschild Cf
ref 4 ds²= dt²(1-rs/r) - dr²(1-rs/r)-1
- r²(dq²+
sin² q.dj²)
avec rs = 2G.M ( G: constante gravitation, M masse centrale
générant le champ de gravitation ): Pour
le Soleil par exemple rs = 3km ( le rayon réel du
soleil est supérieur à 600 000 km !!)
A noter que pour les corps
très denses ou le rayon serait < à rs ( trous noirs ) la signature des coordonnées de
temps et d'espace s'inversent quand r <rs ,
horizon évènementiel.
Deux singularités
apparentes : r = 0 qui est réelle et r = rs qui
peut être éliminée par changement de coordonnées (coordonnées de Kruskal par exemple).
Pour un observateur extérieur, une horloge
tombant vers un trou noir semblera battre de plus en plus lentement ( Il ne la verra jamais franchir l’horizon).
Pour un observateur qui tombe dans le trou
noir c’est différent, sa montre et lui étant dans le même référentiel, il est
très rapidement , inexorablement absorbé, comme projeté en avant dans l’espace vers la
singularité r=0 ( la coordonnée « r » devient de type temps !).
Et plus il lutte, plus c’est court !
Trous noirs de Schwarzschild :
Statique, neutres, un horizon, fontaine blanche, univers multiples, trous de
ver, censure cosmique, perte d'information, évaporation, cas des trous noirs
stellaires, théorème de singularité d'Hawking
Trous noirs
statiques chargés ( Reissner-Nordstrom) : Zéro,
deux, ou double horizons, univers multiples, singularité nue.
Trous noirs en
rotation chargés ou non ( Kerr-Newman):
trois horizons, ergosphère (extraction d'énergie),
singularité en anneau, univers multiples, boucles temporelles
Confirmations de la relativité générale
En l'appliquant la métrique de Schwarzschild
à la lumière (ds²=0)
on trouve la valeur de déviation des rayons lumineux par le soleil 1,7"( 2 fois la valeur classique) et pour le champ central du
soleil la rotation du périhélie de Mercure
43" 03 par siècle à comparer
à 43" 11 +/-0,45" mesuré .
En
RG dans la métrique de Schwarzschild,
le"potentiel central gravitationnel" vaut
V (
r ) =e(1/2 –Gm/r )+
L²/2r² - GmL²/r 3
(L moment
angulaire unitaire, e = 0 particule non massive ou 1 si massive )
Confirmations récentes
de la Relativité Générale (1997)
Ondes
gravitationnelles
Détection indirecte par
perte d’énergie de systèmes binaires relativiste lié à
l’émission d’ondes gravitationnelles.
Interféromètres Virgo et Ligo pour détection
directe ( sensibilité 10-22 ) expériences
prochaines
Précession de Lense Thirring
Entraînement du référentiel
par un corps massif en Rotation (conséquence de la RG), en 1997 observation (RayonsX) sur 3
étoiles à neutrons et 5 trous noirs. Satellite Gravity
Probe B à venir.
Effet Shapiro (
prédit en 1964)
Non seulement les ondes radio
sont déviées mais elles subissent un accroissement brutal (
200 mS en cas d’occultation de
Mars par le Soleil) du temps de trajet lors d’une occultation. Confirmation en
1976 par les réflecteurs laser posés sur
Mars par sonde Viking à 0,1%.
Précision de
confirmation de la Relativité générale.
Dans des expériences récentes
( pulsars binaires) la précision de confirmation
atteint 10-14 , limitation due à la précision des horloges
terrestres ( 10-17 à venir ). A titre d'exemple la théorie quantique
la mieux vérifiée l'electrodynamique quantique est
vérifiée avec une précision de 10-11
Annexe 3: cf ref 4
La solution de Schwarzschild s'obtient de
la façon suivante:
Par
raison de symétrie on suppose la solution de la forme
Ds²= A(r)dt² - B( r)dr² - r² (dq²+ sin²q.dj²)
a) On calcule la limite de A
et B pour r = l'infini sachant qu'on tend vers un espace plat. ( facile)
b) On calcule les connexions
métriques Gi,^k,j ( Pour les courageux, car si la plupart sont
nulles, il en reste !)
c) On utilise l'équation Rij =0 pour le champ à l'extérieur de la masse pour obtenir
un jeu d'équations A ( r), B ( r)
d) On combine les équations
obtenues en c) pour déduire A'( r).B( r) + B'( r). A( r) =0 c.a.d A(r).B( r) = Cte. A) est utilisé pour déterminer cette constante. On
montre que d²(r.A( r)/dr²=0
et on résout ce qui donne A(r ) =(1-rs/r) ou rs est
une constante.
e) Par utilisation de la
limite de Newton on montre que rs = 2Gn.M
10-L'élaboration laborieuse de la
théorie
L'élaboration
de la RG qui durée 10 ans n'a pas été sans erreurs et fausses pistes.
Après avoir tenté sans succès
d' adapter les équations de Newton à la RR (1907) ( le groupe de transformation
de Lorentz de la RR , est inadéquat du fait qu'il transforme tout le
référentiel, alors que la transformation ne peut être que locale), la
reconnaissance formelle du principe d'équivalence ( 1911) et un premier calcul (faux) de la déviation
des rayons lumineux par le soleil (0,83"), en 1912 Einstein tente de
généraliser l'équation de Poisson dans une théorie scalaire qui se révèle être
une impasse
En 1913, Einstein prenant
conscience de l'intérêt des travaux de Gauss et Riemann ,
avecl'aide de Grossmann,
s'est tourné vers une solution généralement covariante qu'il a délaissé pour
une covariance limitée aux transformations linéaires parce qu' il ne retrouvait
pas l'approximation de Newton aux champs faibles et qu'il pensait que cela
violait le principe de causalité.
Convaincu de tenir enfin la solution , il doit déchanter devant les prédictions fausses
de cette théorie (18" pour l'avance du périhélie de Mercure). Après cette épisode de covariance limitée des équations, il
revient à la covariance générale dans la synthèse finale de 1916 qui constitue
la version actuelle de la théorie.,
11-L'approximation Newtonnienne
11-1 Loi du mouvement
(équation géodésique)
La Loi de Newton qui traduit que
l'accélération ne dépend que du "champ de gravitation" cf ref 4
avec F = -GM/r : Potentiel gravitationnel
statique de Newton dont dérive la" force" et i de 1 à 3 ( x,y,z)
est en fait une équation géodésique et doit se comparer à l'équation Géodésique de la RG :
( L'équivalent de l'équation de la gravitation est
l'équation de Poisson)
d²xk/ds²
+ Gikj .(dxi/ds)(dxj/ds) =0 ou
d²xk/dt²
+ Gikj .(dxi/dt)(dxj/dt) =0 (2)
Avec t= temps propre , c.dt = ds et comme on a posé
c=1, en valeur dt = ds
Rappelons que dx0
est la coordonnée de temps ( en fait c.dt), les autres dxi étant
les coordonnées d'espace (x,y,z).
Dans l'approximation Newtonienne ( champs faibles et
statiques, vitesses faibles), on peut
alors ne retenir dans (2) que les expressions relatives à (dx0/ds).(dx0/ds) ( soit i=j=0 dans l'équation (2) qui sont très grandes par rapport aux autres ( car
c.dt>> dx,dy,dz) soit:
d²xk/dt²
~ - G0k0.(dx0/dt)(dx0/dt)
= - G0k0.(dt/dt)(dt/dt) (3)
Rappelons l'expression des symboles de
Christoffel ( connexion métrique) qui interviennent
dans l'équation géodésique
Gikj = 1/2(Glk )( ¶Gjl/¶xi + ¶Gil/¶xj - ¶Gij/¶xl
) (4)
Pour évaluer (3) à partir de l'expression générale (4) on voit
qu'il faut connaître les Gij
Dans
l'approximation champ faible stationnaire, la métrique étant quasi Minkowskienne,
on peut représenter les éléments de la métrique par
hij
étant le tenseur métrique de Minkowski* et Hij étant
un infiniment petit du premier ordre
considéré comme une perturbation.
*Attention , on rencontre 2 formulations de signe opposés de hij , nous avons pris la
convention +1,-1,-1,-1 dans cet
exposé
De plus, avec i=j=0, sachant que la
métrique de Minkowski est diagonale, Gjl , Gil sont nuls sauf pour l=i=j=0 soit:
G0k0 = 1/2( Glk)(
¶G0l/¶x0
+ ¶G0l/¶x0 - ¶G00/¶xl ) =
1/2( Glk)(
-¶G00/¶xl ) (5)
i,j,k,l
Les termes en rouge sont nuls ( dérivées par rapport au temps d'un phénomène statique)
G00=
1+H00 est l'élément de la métrique lié à la
coordonnée x0 ( temps) il vient:
¶G00/¶xl = ¶(1+H00)/¶xl = ¶(H00)/¶xl (6)
G0k0 = -1/2( Glk) ¶(H00)/¶xl (7)
Calculons le tenseur
métrique inverse les éléments non diagonaux sont négligeables ( perturbations), restent les éléments diagonaux
Glk
= 1-Hlk
~1, pour l=k
= 0 et Glk = -1-Hlk ~ -1 pour
l=k = 1,2,3 soit G0k0 = 1/2.¶(H00)/¶xk (8)
car Hll
est
une perturbation petite devant 1.
Glk sera utilisé pour l=k=1,2,3 ,car pour l=0 (
temps ) le produit par la dérivée
associée ¶G00/¶x0 est
nul
En
reportant dans (3) et en renommant les indices" l,k
"égaux " i " , en remplaçant dx0 par dt,
on obtient
d²xi/dt²=
-1/2(dt/dt)².dH00/dxi ( en renommant l'index k en i) (9)
Pour i= 0 c'est à dire pour la coordonnée dt
l'équation (6) s'annule car H00 est statique : d²t/dt²=
0
On
déduit dt/dt
= cte,
En divisant alors les deux membres de l'équation (9) par
(dt/dt)²
, facteur constant, on obtient
d²xi/dt²= - 1/2(dH00/dxi) =-
1/2(d(1+H00)/dxi)= - 1/2(dG00/dxi)=-dF/dxi
(1) (10)
ce qui est la loi de Newton en posant de
façon générale H00 = 2F
+cte , compte tenu que pour H00
= 0 le champ doit être Minkowskien , la constante est nulle.
On en déduit G00 = 1 +2F
Remarquons comment à la
notion classique de potentiel gravitationnel F, on fait correspondre en Relativité
Générale une Courbure de l'Espace Temps H00
11-1-b :
Approximation Newtonnienne (synthèse)
Trois conditions: (1)-Vitesse
des particules v <<c, (2)-Champ faible, (3)-Champ
statique.
Rappel
Newton :
d²xi/dt²= - dF/dxi : F = potentiel gravitationnel (-GM/r) (1)
Rappel
Equation géodésique (ds=dt)
d' Einstein: d²xs/d²t+
Gmsn
.(dxm/dt)(dxn/dt) =0 (2)
(1) dx0= cdt >>dxi on néglige ces
dernières: (2) devient: d²xs/d²t ~ - G0s0.(dt/dt)² (3)
Rappel
Connexion métrique:
Gmsn
= 1/2(Grs )( ¶Gnr/¶xm
+ ¶Gmr/¶xn - ¶Gmn/¶xr
) (4)
Calcul de G
en fonction des hypothèses précédentes m=n=0
G0s0 = 1/2( Grs)(
¶G0r/¶x0
+ ¶G0r/¶x0 - ¶G00/¶xr
) = 1/2(Grs)( ¶G00/¶xr) (3) (5)
Gmn=hmn+Hmn soit
G00 = 1+H00 et ¶G00/¶xr = ¶(1+H00)/¶xr = ¶(H00)/¶xr Métrique
quasi-RR (2) (6)
Grs=
-1-Hrs ~-1, Avec r=s=1,2,3 soit G0s0 =1/2¶H00/¶xs Calcul
avec métrique quasi-RR (2) (8)
d²xi/d²t=
-1/2(dt/dt)².dH00/dxi report dans (3) et
comme d²X0/dt²=0, dt/dt=cte (9)
d²xi/dt²= -1/2(dH00/dxi) =-dF/dxi (1) , H00= 2F, G00 = 1+2F, On a divisé (9) par (dt/dt)² (10)
11-2
Approximation de la loi de Poisson
On déduit la loi de Poisson
de l'équation de la gravitation par la même méthode.
Rappelons l'équation de la
gravitation de la RG
Rij-1/2Gij.R= - 8p.G.Tij elle
peut aussi s'écrire Rij= - 8p.G.(Tij -1/2(Gij.T)) (1)
Dans le cas de l'approximation de Newton,
le tenseur d'énergie de la matière est déterminé par r
densité de matière au sens étroit. Toutes les composantes de Tij s'annulent sauf pour T00 =r =T, Tij
= T = r (2)
Rappelons la formulation du tenseur de
Ricci Rij=
¶Gikj/¶xk-
GiklGjlk (3)
Pour les mêmes raisons que
précédemment les composantes Gij
autres que G00 sont négligées ainsi que les dérivées par
rapport au temps. Le terme GiklGjlk de
(3) est négligé car du second
ordre. Il reste en développant:
Rij
~ ¶Gikj/¶xk
= ¶Gi0j/¶x0 + ¶Gi1j/¶x1
+ ¶Gi2j/¶x2 + ¶Gi3j/¶x3
en développant G
en fonction des Gij pour i=j=0 il vient
¶Gikj/¶xk =-1/2( ¶²G00/¶X1²+ ¶²G00/¶X2²+¶²G00/¶X3²)
= (-1/2) DG00 (4)
En
reportant (2) et (4) dans (1) il vient: DG00
=DH00= 8pG.r
soit l'équation de Poisson DF= 4pG.r
avec G00 =1+2F , H00 =2F car D(1+2F)= 2DF=8pG.r
12- De la réalité physique des
coordonnées en Relativité générale
Ces coordonnées n'ont aucune
réalité physique, ce qui a troublé les physiciens dont Einstein, elles ne sont
pas mesurables par des procédés physiques. (cf ref 2)
Changement de coordonnées
"Il s'agissait donc
d'élaborer une théorie dont les équations conservent leur forme par une
transformation non linéaire des coordonnées. Savoir si cela devait être vrai
pour des coordonnées quelconques ( mais continues) ou seulement pour certaines
transformations , je l'ignorais pour le moment .Je me rendis bientôt compte
qu'avec la conception des transformations non linéaires requises par le
principe d'équivalence, c'en devait être fini de l'interprétation physique
directe des coordonnées: on ne pouvait plus exiger que les différences entre
coordonnées représentent des résultats immédiats de mesures effectuées à l'aide
de règles et d'horloges.
Ce point me tracassa beaucoup
car je restai longtemps incapable de comprendre ce que tout compte fait les
coordonnées doivent représenter en physique.
Je ne réussis à sortir de ce
dilemme qu'en 1912 grâce à la réflexion suivante:
Il fallait trouver une
nouvelle formulation de la loi de l'inertie, qui en l'absence de champ de
gravitation, et en utilisant un système inertiel comme système de coordonnées,
s'identifie avec la formulation galiléenne du principe d'inertie.
Formulation qui dit qu'un
point matériel sur lequel n'agit aucune force est représenté par une droite
dans l'espace temps (4D), c.a.d la ligne la plus
courte ou plus précisément une ligne extrémale.
Ce
concept présuppose celui de longueur
d'un élément de courbe, c.a.d d'une métrique.
En RR la métrique (ds²)quasi Euclidienne est une fonction bien déterminée des
éléments différentiels des coordonnées.
Si on introduit d'autres
coordonnées grâce à une transformation non linéaire , le ds²
reste une fonction homogène des éléments différentiels des coordonnées mais les
coefficients de cette fonction (Gij) ne sont plus des
constantes: Métrique Riemanniene
Les courbes extrémales du
genre temps de cette métrique donnent la loi du mouvement.
Les coefficients décrivent le
champ de gravitation par rapport au système de coordonnées choisi.
On
dispose ainsi d'une formulation naturelle du principe d'équivalence…
Ce ne sont pas aux éléments
différentiels des coordonnées ( qui sont de simples paramètres mathématiques),
mais seulement à la métrique de Riemann qui leur est associée qu'il faut
attribuer une signification physique" Conférence Glasgow 1933
Notons qu' il aura fallu 3 ans à Einstein pour admettre cette
conclusion que les coordonnées ne sont qu’un moyen de décrire qui n’a rien à
voir avec les objets à décrire. Cet état de chose n’est pleinement pris en
compte que par une formulation généralement covariante des lois de la nature.
Toute autre méthode mélange moyen de description et objet à décrire d’ou
confusion.
Une des conséquences est la
difficulté de définir les paramètres ( position,
vitesse etc..) des objets très éloignés.
Dans un espace de type
riemannien ou le référentiel galiléen est défini localement, les concepts
développés par Einstein pour arpenter et synchroniser un référentiel ne
s'appliquent que localement . Comment prolonger ce
référentiel local jusqu'aux points éloignés de l'univers auxquels on veut se
"connecter" pour faire des mesures physiques, comparaisons par
coïncidence de points évènements des deux référentiels. ( la
métrique dépend de nombreux paramètres, le temps ne s'écoule pas partout de la
même façon, la non linéarité est la règle )
En RR pas de problème la
transformation de Lorentz étant linéaire tout le référentiel est balisé en
espace et en heure ( on définit le synchronisme). On
peut alors faire coïncider les points évènements de deux référentiels quelque
soit leur position dans le référentiel même très éloignés, car il y aura un
point du référentiel au contact dont la position spatio-temporelle est définie
par rapport à l'observateur .On n'a rien de tel en RG. Tout ceci pour dire que
le mouvement de récession apparent des galaxies lié à l'expansion n'est
nullement en contradiction avec la limite de vitesse de la RR. Même pour les
formulations les plus récentes de la RG (dans un formalisme commun à la
mécanique quantique et à la théorie des cordes),ce
point est hors du cadre de leur portée, ce qui fait dire que la question est
grammaticalement incorrecte.
13- Conclusion
A partir de deux hypothèses très
simples ( comme
en RR)
- Généralisation du principe de Relativité aux
systèmes non inertiels
- Principe d'équivalence
Einstein ramène la gravitation à un
problème cinématique par le principe d'équivalence.
L'espace de Minkowski ou la RR s'applique est un des
référentiels les autres s'obtenant par "simple" changement de
coordonnées.
Pour satisfaire au principe de Relativité les
équations doivent garder la même forme quel que soit le référentiel.
Compte tenu du type de changement de coordonnées , pour satisfaire à ce critère les équations
doivent être écrites sous forme d'équations entre tenseurs covariants.
Elle se réduit à une seule
équation d'apparence très simple ( en fait très
synthétique puisque une égalité tensorielle suppose l'égalité de toutes ses
composantes), mais très complète.
R=T
qui signifie que localement la géométrie de
l'espace-temps ( cf Relativité Restreinte) est
conditionnée par l'énergie ( sous toutes ses formes , cf
RR) localement présente.
C'est en fait une théorie de la gravitation.
Le concept révolutionnaire ( se rappeler la révolution héliocentrique de
Galilée, contre les apparences)
exposé par EINSTEIN est que la gravitation n'est pas une force comme NEWTON
l'entendait mais la conséquence de la géométrie de l'espace temps. Les corps
qui suivent des trajectoires courbes au voisinage de masses (
s'ils ne sont soumis à aucune autre influence ), ne font que suivre les
géodésiques ( chemins naturels de moindre effort) de l'espace temps.
Ceci rend bien compte que
cette trajectoire est indépendante de la masse du corps ,
de sa nature et de sa forme
Cette théorie , force
l'admiration par sa puissance synthétique, et l'audace de ses concepts en même
temps que par la limpidité des idées développées.
Elle est la grande théorie rationaliste du vingtième siècle ( la mécanique quantique étant en rupture avec le
rationalisme) Elle prédit des phénomènes qui débordent son champ d'action (
force ou faiblesse ?)
Pour autant elle n’est pas une théorie du
passé, comme le montre les découvertes récentes
prédites.
La
formulation moderne de la RG dans un langage commun à la mécanique quantique
déduit l’équation de la RG, non pas d’une généralisation de l’équation de
Poisson, mais comme conséquence du principe de moindre action *caractérisée par le Lagrangien :
SH = òdnx. LH , avec LH ( densité de Lagrangien) = (-g)1/2.
R avec « g » déterminant du tenseur métrique et R scalaire de Ricci dérivant par contraction successives du
tenseur de Riemann contenant les informations de courbure, et extremum sur la trajectoire.(cf ref 12)
On sait que la Lagrangien , notion de mécanique
classique ( Energie potentielle - Energie cinétique :L= 1/2m( px²+py²+pz²) -U (x, y,z) à son équivalent
en mécanique quantique par l’intermédiaire d’ opérateurs ( i¶/¶x etc..) agissant sur la
fonction d’onde y permettant
une quantification.
Ce Lagrangien très simple peut être généralisé dans
différentes directions permettant de généraliser la théorie .
* Hilbert avait déduit
l’équation de la Gravitation par cette méthode, en s’appuyant sur les travaux
d’Einstein à peu près en même temps qu’Einstein.
Généralisation du
Lagrangien :
-
La
Constante cosmologique : LH= (-g)1/2.
(R - L) qui conduit par calcul de quantification de
l’énergie du vide, 2p. E0 = ½ hw à L~
m4p avec mp
= masse de Planck (valeur astronomique de cette constante, en désaccord énorme
avec l’observation ).
-
-
On
peut aussi introduire des ordres supérieurs à 2 dans la dérivée de la métrique
(difficultés liées au
conditions initiales et à la Re-normalisation
déjà pas résolue avant, et qui se complexifie encore)
-
On
peut introduire des tenseurs dans le Lagrangien qui conduit à une variation de
la « constante G » dans le temps.
-
On
peut considérer le cas d'une torsion non nulle ( ne
change pas la forme des équations)
-
Etc..
-
Enfin la « géométrisation » de la
théorie ( la RG rentre dans la classe des
théories qui n’ont pas de coordonnées préférentielles) permet d’en élargir la
portée et débouche sur la théorie des supercordes
développée dans ce même cadre rationaliste et qui est une tentative
d'unification des grandes théories
modernes.
14- Références Bibliographiques
(1) Encyclopédie
Univervalis ( Relativité
générale)**
(2)
Albert Einstein , Oeuvres choisies
Vol 2 ( Relativité 1) Seuil /CNRS***
(3) Albert Einstein , Oeuvres choisies Vol 3 ( Relativité 2) Seuil
/CNRS***
(4) Cosmology
and Particle astrophysics ( lars
Bergström) Wiley***
(5) Les
trois étapes de la Cosmologie ( J. Merleau Ponty, Bruno Morando) Laffont*
(6)
Astronomie & Astrophysique ( Marc
Séguin, Benoît Villeneuve ) Masson*
(7)
http://math.ucr.edu/home/baez/gr/outline2.html*
(8) Notes de
cours d'analyse tensorielle ( INSA Lyon 1966)**
(9) Temps ,Espace , Matière , Leçons sur la théorie de la
Relativité Générale (Herman Weyl - 1922) .
Blanchard****
(10) Les
trois premières minutes de l'univers . (S. Weinberg )Seuil*
(11) La
nature de l'espace et du temps ( S.Hawking
R. Penrose ) Gallimard****
(12)http://nedwww.ipac.caltech.edu/level5/march01/Carroll3/Carroll01.html****
(13) http://cdfinfo.in2p3.fr/culture/Cosmologie**
(14) Introduction à la
relativité générale ( Luc Blanchet)***
** moyen
*** difficile
****très difficile
15 – Glossaire
Fondement de la
Relativité générale
Impulsion-Energie
en RR
Métrique en Relativité restreinte
Métrique de Robertson Walker en Relativité Générale
Métrique de Schwartzschild
en Relativité Générale
Principe d’extension de Relativité



 .
.