#metrique, #newton, #pe, #post_n, #principe_r,
#quantif, #Rayonne, #redshift, #ref_ch_l, #rg,
#theorie_r, #TN, #TN1,
#TN2
RELATIVITÉ par Thibault DAMOUR, docteur ès
sciences, directeur de recherche au CNRS, membre correspondant de l'Académie
des sciences.
En physique, le vocable " relativité " recouvre deux concepts très différents. Celui de relativité
restreinte (qui a remplacé
la relativité galiléenne) spécifie la structure cinématique de l’espace-temps.
Cette structure, d’abord suggérée par l’étude de l’électromagnétisme, a fourni
un cadre général pour la description de toutes les autres lois fondamentales de
la nature, à l’exception de la gravitation, dont la formulation constitue le
domaine de la relativité générale. Cette dernière théorie apporte une modification profonde au
concept d’espace-temps, lequel cesse d’être une arène neutre, servant de simple
cadre de déploiement à l’existence et à l’évolution de la matière, pour devenir
une entité dynamique, influencée par et influençant la distribution d’énergie
qu’il contient, et évoluant au même titre que les autres champs physiques.
Cependant, la relativité générale est restée longtemps en marge du développement
général de la science, car elle apparaissait comme une théorie mal confirmée et
peu utile. Cette situation a changé depuis les années 1960 grâce à divers
facteurs : développement de
la gravitation expérimentale, découverte des quasars, des pulsars, etc.,
exploration théorique du régime des champs gravitationnels forts (objets
condensés, trous noirs) et de celui des champs gravitationnels rapidement
variables (rayonnement gravitationnel). De plus, les tentatives modernes d’unification
des interactions fondamentales dans le cadre de la théorie quantique des champs
ont suscité des recherches nouvelles sur les rapports entre la relativité générale,
la théorie quantique et les autres forces, stimulant par là la création, ou le
développement, de nouvelles théories physiques, comme la supergravité ou la théorie
des cordes.
1.
Relativité galiléenne et relativité restreinte
Principe de
relativité
Il convient d’abord de distinguer le
principe de relativité, qui est commun à Galilée et à Einstein, des théories de
la relativité. Le principe de relativité stipule l’existence d’une classe particulière
de systèmes de référence par rapport auxquels les lois de la physique locale (c’est-à-dire
les lois d’évolution des phénomènes expérimentaux dont on contrôle les
conditions initiales et les conditions aux limites dans un laboratoire de
taille finie) prennent exactement la même forme. Rappelons que par système de référence
(ou référentiel, ou repère, ou système de coordonnées) on entend une procédure
expérimentale, utilisant des corps solides et des horloges " de référence ", qui permet d’attribuer univoquement à
tout événement une date t
et une position spatiale (x , y , z ) = (x 1, x 2, x 3). Parmi les lois de la physique locale, on admet
la géométrie euclidienne pour décrire la juxtaposition des corps solides, ainsi
que le principe d’inertie. On admet aussi que la classe particulière des référentiels
où est valable le principe d’inertie (dits encore référentiels inertiels) est décrite
par dix paramètres, correspondant à des changements d’origine du temps et de l’espace,
à des rotations euclidiennes constantes et à des déplacements relatifs à
vitesse constante. Notons que le principe de relativité constate, sans l’expliquer,
l’existence de repères privilégiés où les lois de la physique revêtent une
forme simplifiée. Le fait empirique que ces repères sont, avec une bonne
approximation, non accélérés par rapport aux étoiles fixes reste incompris. Une
détermination théorique satisfaisante des repères inertiels eux-mêmes, en
fonction, par exemple, de la distribution de la matière dans l’univers
(principe de Mach), n’existe pas actuellement. La relativité générale améliore
cette situation théorique sans cependant apporter une réponse définitive.
Beaucoup d’expériences appuient le principe de relativité, depuis la pratique
journalière – on ne sent
aucun effet de la vitesse dans un train ou dans un avion en mouvement
rectiligne uniforme – jusqu’aux
répétitions modernes des expériences de Michelson-Morley ou de Hughes-Drever,
qui vérifient l’isotropie des lois de la physique locale avec une précision
inouïe.
Après le principe de relativité,
considérons maintenant les théories de la relativité, c’est-à-dire l’ensemble
des lois cinématiques (lois de transformation entre repères inertiels) et
dynamiques (physique locale) qui satisfont au principe de relativité. En ce qui
concerne les lois cinématiques, il est remarquable qu’elles soient presque
uniquement déterminées sous des hypothèses faibles et générales (homogénéité et
isotropie de l’espace-temps, absence de violations grossières de la causalité),
plus la remarque que l’ensemble des transformations entre repères d’inertie
doit avoir une structure de groupe (l’application de deux transformations
successives doit être équivalente à l’application d’une seule transformation).
En effet, il n’existe que deux solutions possibles.
La première est le groupe des
transformations de Galilée :
![]()
où Rij est une matrice orthogonale (dab Ria Rjb = dij ) représentant une rotation générale dépendant
de trois paramètres (indices latins i , j = 1, 2, 3 ; dij est le symbole de Kronecker qui vaut 1 si i = j et
0 si i ¹ j , et on utilise la convention de sommation d’Einstein sur tout
indice répété). Ce groupe est caractérisé par l’existence d’un temps absolu (c’est-à-dire indépendant du référentiel). La
théorie de la relativité correspondante est celle de Newton, avec des lois du
mouvement déterminant les accélérations des corps en fonction de la
configuration géométrique relative instantanée du système en interaction.
La seconde solution est le groupe des transformations
de Lorentz-Poincaré :
![]()
où habLmaLnb = hmn (indices grecs = 0, 1, 2, 3 ;
x 0 = ct ; hmn est une matrice diagonale dont les seuls éléments
non nuls sont h00 = - 1
et h11 = h22 = h33 = + 1). Ce groupe est caractérisé par l’existence d’une
vitesse absolue c (indépendante du référentiel). Avec une paramétrisation
convenable de Lmn (et a 0 = cb ),
la limite formelle quand c ® ¥ des transformations de Lorentz-Poincaré
redonne celles de Galilée (le processus formel de limite c ® ¥ est un exemple de ce qui s’appelle contraction
de groupe en mathématiques). C’est la réflexion d’Einstein, de 1895 à 1905, sur
l’incompatibilité entre la validité (attestée par beaucoup d’expériences) d’un
principe de relativité pour les phénomènes électromagnétiques, et la
non-invariance des équations de Maxwell sous les transformations de Galilée
(1), qui l’a conduit à remplacer ces dernières par les transformations de
Lorentz-Poincaré (2), considérées comme la base d’une nouvelle théorie de la
relativité (la vitesse absolue c étant identifiée par Einstein à la vitesse de la lumière). Pour l’étude
des conséquences cinématiques remarquables de (2) [relativité de la simultanéité,
dilatation des durées, contraction des longueurs, nouvelle structure causale,
loi non linéaire d’addition des vitesses], voir l’article ESPACE-TEMPS.
Contentons-nous ici de rappeler que le groupe de Lorentz-Poincaré est le groupe
des transformations qui laissent invariant l’intervalle d’espace-temps :
![]()
elles sont donc les analogues à quatre
dimensions (mais avec la présence d’un signe moins pour le temps) des rotations
de l’espace euclidien ordinaire, qui laissent invariant l’intervalle (carré) de
longueur ds ² = dij dxi dxj . Autrement dit, l’espace-temps de la relativité
restreinte est muni d’une structure géométrique absolue définie par la métrique
quadratique (3) [espace-temps de Minkowski à 4 dimensions]. Attention au fait que, malgré ce
que pourrait laisser croire la notation usuelle " ds²", la forme quadratique (3) n’est pas définie positive.
Depuis 1905, la physique s’est efforcée
de formuler ses lois sous une forme invariante sous les transformations (2).
Cette tâche s’est révélée très fructueuse, car elle a conduit à la découverte
de nouvelles lois et à la prédiction de nouveaux phénomènes, surtout dans le
domaine quantique. Citons, entre autres : la dynamique relativiste des particules, la théorie relativiste
des particules de spin 1/2 de Dirac, la prédiction de l’antimatière, la
relation E = mc² entre l’énergie
et la masse inertielle, la relation entre spin et statistique et le théorème
CPT. Ce dernier théorème exprime la symétrie de tout système sous le produit
simultané des trois transformations suivantes : conjugaison de Charge (remplacement matière ↔ antimatière), Parité (transformation dans un miroir) et
renversement de la direction du Temps. Nombre de conséquences de ces lois se vérifient
quotidiennement dans les collisions de particules élémentaires et dans les réactions
nucléaires (cf. chimie NUCLÉAIRE,
énergie NUCLÉAIRE, forces NUCLÉAIRES, PARTICULES ÉLÉMENTAIRES). À l’heure
actuelle, la cinématique de la relativité restreinte sert de cadre à la plupart
des modélisations théoriques de la physique microscopique (théories des
interactions électrofaibles et fortes). Seule la gravitation joue un rôle
particulier : d’une part,
parce que la généralisation directe, covariante sous le groupe de
Lorentz-Poincaré, de l’équation de Poisson DU = - 4 prG qui détermine
le potentiel newtonien, est inadéquate, d’autre part, pour des raisons plus
profondes liées, comme on va le voir, au principe d’équivalence. Il appartenait
à la théorie de la relativité générale d’Einstein (1915) de transcender ces
difficultés de manière imprévue.
Masse inertielle
et masse gravitationnelle
Le fait expérimental fondamental qui a
conduit à la relativité générale est l’égalité entre la masse inertielle et la
masse gravitationnelle (cf. DYNAMIQUE). Les expériences de Galilée sur la chute des
corps suggéraient déjà que l’accélération due au champ de gravitation de la
Terre est indépendante de la masse et de la nature des corps (cf. GRAVITATION). Les premières expériences
modernes démontrant cette égalité avec une haute précision sont celles du baron
Roland von Eötvös. La précision de ce type d’expérience a été considérablement
affinée par Robert H. Dicke
et Vladimir B. Braginskii
(qui utilisaient l’accélération due au champ de gravitation du Soleil) et, plus
récemment, par Eric G. Adelberger.
On sait maintenant, grâce à ces expériences extrêmement délicates, que le
rapport entre la masse inertielle et la masse gravitationnelle (qui est
constante pour chaque substance) est une constante universelle pour toute la
matière, la précision de mesure atteinte (de l’ordre de 10-12) étant l’une des meilleures de toute la
physique. Afin de comprendre la signification de ce résultat, il convient d’examiner
la définition des deux types de masse dans la dynamique galiléenne de Newton.
On y suppose que tout corps possède une masse inertielle spécifique m I qui mesure sa réponse à la sollicitation de n’importe quelle
force extérieure. Elle est déterminée de façon purement cinématique par la loi
d’action et de réaction, qui entraîne la loi de conservation de la quantité de
mouvement : Relativement à un
corps de référence (m 0I), le rapport m I/m 0I est l’inverse de celui des variations de leurs vitesses au cours
d’une collision élastique mutuelle ;
quant à la masse gravitationnelle mg , elle intervient dans l’expression du
mouvement d’une particule soumise à une force particulière, la gravitation.
Cette masse détermine l’intensité de l’attraction éprouvée par ce corps dans un
champ de potentiel gravitationnel U au moyen de l’équation de Newton :
![]()
Alors que m I et mg sont des propriétés intrinsèques du corps, U
est une propriété du milieu extérieur. (La description newtonienne, moins précise,
du phénomène de gravitation est provisoirement utilisée ici afin d’aider à
comprendre qualitativement celle de la relativité générale.)
La masse gravitationnelle est donc
tout à fait analogue à la charge électrique e d’une particule, laquelle détermine la réponse
d’un corps à la sollicitation d’un potentiel électrique extérieur V, d’après
:
![]()
Étant donné que le rapport e/m
I peut prendre des valeurs très différentes
selon les corps considérés (y compris la valeur zéro), il n’y a pas a priori de
raison implicite dans la gravitation de Newton de s’attendre à une valeur
constante du rapport mg /m I. Les résultats
de Eötvös-Dicke sont par conséquent remarquables, surtout si l’on considère que
la masse inertielle d’un corps macroscopique comprend non seulement la somme
des masses de ses constituants (nucléons et électrons), mais aussi, d’après E
= mc², la contribution
des diverses énergies de liaison et de mouvement de ces constituants. La précision
expérimentale actuellement obtenue permet de vérifier l’équivalence dans m I et mg des
contributions de l’énergie de liaison nucléaire, de l’énergie cinétique des
nucléons dans le noyau, de l’énergie électrostatique entre protons et de l’énergie
de liaison atomique entre électrons et noyau. Par ailleurs, une analyse très précise
du mouvement relatif Terre-Lune (utilisant des réflecteurs lasers laissés sur
la Lune par Apollo-11, -14 et -15, et par Lunakhod-2) a permis de vérifier que
même l’énergie de liaison gravitationnelle contribue de façon équivalente à m
I et à mg . Il existe aussi des preuves directes de la
validité de l’équivalence à l’échelle d’une particule élémentaire individuelle,
le neutron. Ces résultats constituent la base du principe d’équivalence : À des quantités égales d’énergie d’origine
quelconque correspondent des masses gravitationnelles identiques.
Référentiels
localement inertiels
L’universalité de l’équivalence entre
masse inertielle et masse gravitationnelle a des conséquences importantes pour
la notion de référentiel inertiel. La première conséquence est qu’il n’existe
pas de particules " neutres
" par rapport à l’interaction
gravitationnelle (même la lumière, puisqu’elle est un paquet d’énergie électromagnétique,
doit graviter, ce que l’expérience vérifie). Il est donc impossible, même en
principe, de construire des référentiels " non accélérés ", puisque tout dispositif physique sera
sensible à l’accélération gravitationnelle causée par toutes les masses extérieures
au système, même si elles sont très lointaines et invisibles. Une seconde conséquence
vient cependant tempérer cette conclusion négative. D’après l’équation (4), l’équivalence
de m I et mg signifie que tout corps (et tout paquet d’énergie)
tombe, dans un champ gravitationnel, avec exactement la même accélération a = ÑU.
Cette " universalité de
la chute libre "
implique que si l’on réalise, localement, un " repère en chute libre " en utilisant des solides et des horloges
de référence en chute libre, tous les corps dans le voisinage immédiat du repère
apparaîtront comme non accélérés par rapport à lui. Donc, par rapport à un tel
repère, tout champ gravitationnel extérieur est " effacé ". Toutefois, l’effet du champ de gravitation ne peut être éliminé
qu’à l’intérieur d’une région suffisamment petite pour que le champ y soit
uniforme : ainsi, il y a en réalité
une légère convergence latérale des occupants d’un ascenseur en chute libre,
chacun d’eux tombant vers le centre de la Terre.
L’analyse précédente conduit au
principe suivant : Puisque
tout champ de gravitation, si intense ou rapidement variable soit-il, est
pratiquement constant dans une région suffisamment petite de l’espace-temps, il
peut être effacé localement. Or on sait que, en l’absence de gravitation, les
autres lois de la physique sont valables dans les systèmes inertiels. Il est
donc raisonnable de postuler que les référentiels particuliers qui éliminent
localement la gravitation sont en même temps des systèmes inertiels, dans
lesquels les lois de la physique locale, auxquelles se réfère le principe de
relativité, sont valables. Cette assertion constitue le principe d’équivalence
généralisé, supposé applicable à tout système physique. Comme tous les
principes de la physique, celui-ci ne découle pas d’une nécessité logique, mais
doit être confronté à l’expérience. On pourrait en effet concevoir pour les
champs de gravitation des manifestations locales différentes de celles de la
gravitation newtonienne, susceptibles d’altérer les lois habituelles de la
relativité restreinte. Exprimé dans le langage usuel de la théorie des champs,
notre postulat suppose que le couplage gravitationnel est universel et minimal,
au moins à l’échelle macroscopique.
Décalage
vers le rouge ou dilatation gravitationnelle des durées
Les référentiels localement inertiels,
au voisinage de la Terre, par exemple, au lieu d’être attachés à la Terre, sont
donc des ascenseurs en chute libre; ce fait paradoxal a pour conséquence expérimentale
le décalage des fréquences des raies spectrales vers le rouge (ou red shift
) dans le champ de gravitation terrestre.
La prédiction de cet effet illustre clairement le principe d’équivalence généralisé
énoncé ci-dessus. Considérons deux observateurs, chacun instantanément au repos
par rapport à la Terre, l’un à la surface de la Terre, l’autre à l’altitude h . Une onde lumineuse est émise vers le haut et
sa fréquence est mesurée à l’altitude h (avec le résultat ωh ) et comparée à la fréquence ω0 mesurée à la surface de la Terre. Si le référentiel
attaché à la Terre était inertiel, deux observateurs dans ce référentiel n’observeraient
aucun changement de fréquence, car les équations de Maxwell, valables seulement
dans les systèmes inertiels, attribuent une fréquence constante à une telle
onde se propageant librement. Le principe d’équivalence affirme au contraire
que les équations de Maxwell sont valables dans des systèmes (accélérés)
tombant en chute libre. Dans un tel système, l’observateur à la surface de la
Terre tombe en chute libre, mais sa vitesse par rapport à la Terre est encore
nulle tandis qu’il mesure la fréquence ω0. Un troisième observateur qui serait situé à
la hauteur h dans le
même référentiel en chute libre n’observerait à l’arrivée de la lumière aucun déplacement
de fréquence, les lois de Maxwell étant également valables pour lui. Cependant,
lorsque la lumière atteint h, au bout d’un temps t
= h/c, cet observateur a atteint, par rapport à la Terre, la vitesse v
= gh/c, où g = 9,80 m
. s-2 est l’accélération locale près de la surface de la Terre. L’observation
réelle en h étant effectuée
par un appareil, également en chute libre mais à vitesse nulle par rapport à la
Terre en cet instant t ,
celui-ci possède par conséquent une vitesse - gh/c par
rapport au troisième observateur. Or, en relativité restreinte, les fréquences
mesurées par deux observateurs en mouvement relatif sont différentes (effet
Doppler-Fizeau). Pour une vitesse relative faible, l’effet Δω/ω est
égal à v/c .
On trouve ici :
![]()
soit un déplacement vers le rouge.
Numériquement, l’effet est extrêmement
faible :
![]()
il a cependant été mesuré au moyen de
l’effet Mössbauer (cf. effet
MÖSSBAUER), avec une précision de 1 p. 100, par Robert V. Pound
et ses collaborateurs. D’un point de vue plus général, puisque la fréquence d’une
raie spectrale définit une " horloge
" à l’échelle atomique, le principe
d’équivalence prédit l’existence d’une dilatation gravitationnelle des durées
lors de la comparaison de deux horloges situées à des niveaux de potentiel
gravitationnel différents. Une expérience très précise (2 p. 10 000)
de Robert F. C.
Vessot et ses collaborateurs utilisant
une horloge à maser à hydrogène emportée dans une fusée à une altitude de 10
000 kilomètres a ainsi donné une autre vérification directe du
principe d’équivalence généralisé.
Le principe d’équivalence permet de
formuler toutes les autres lois de la physique, en présence d’un champ de
gravitation, dans des régions infiniment petites. Il est cependant nécessaire,
afin de tirer les conséquences de ces lois en résolvant leurs équations, de
relier entre elles les régions possédant des référentiels d’inertie locaux différents.
Cette opération mettra en évidence les effets de la gravitation sur la matière
(le problème inverse, celui de la détermination des champs de gravitation, sera
traité plus loin, au chapitre 3,
lorsqu’on établira les équations d’Einstein de la relativité générale). Afin de
relier entre eux les différents référentiels, on peut introduire un système de
coordonnées unique, qui en général n’est pas partout inertiel, et exprimer les
lois de la physique dans ce système étendu.
Soit Xa les coordonnées d’un référentiel localement
inertiel. Dans un tel référentiel, les lois de la relativité restreinte s’appliquent.
En particulier, on y mesure l’intervalle d’espace-temps :
![]()
ainsi que, par exemple, les densités
et flux locaux d’énergie et d’impulsion qui se rassemblent dans les composantes
du tenseur d’énergie-impulsion Tab. Quand on change
de référentiel localement inertiel (au voisinage du même point de l’espace-temps)
par une transformation de Lorentz, ds² est invariant alors que Tab se
transforme comme un tenseur de Lorentz (T’ γδ
= Λγα Λδβ
Tab). En
revanche, les transformations qui conduisent au référentiel non inertiel étendu,
de coordonnées xµ, sont en général non linéaires
: Xa = Xa(xµ). La
valeur de l’invariant ds² calculée dans le système étendu xµ
s’obtient en écrivant, au voisinage de chaque point :
![]()
d’où :
![]()
où l’on a défini, point par point,
![]()
L’espace-temps apparaît ainsi comme
muni non plus simplement d’une métrique quadratique minkowskienne (3) avec des
coefficients constants, mais de la métrique quadratique plus générale (6). Ces
espaces métriques plus généraux ont été étudiés d’abord par Gauss puis par
Riemann et sont des géométries riemanniennes (cf. GÉOMÉTRIE, chap.
6, et VARIÉTÉS DIFFÉRENTIABLES). Ils sont munis d’une notion de différentiation
covariante ![]() µ qui
se réduit à la dérivation partielle usuelle ∂α = ∂/∂Xα dans
les référentiels localement inertiels [maintenant définis, de façon cohérente,
à partir de la structure riemannienne (6) comme les transformations X α = X α (x µ) qui réduisent,
autour d’un point donné x0, la forme (6) à la forme (5)
modulo des termes du second ordre
en X α
- X α(x
0)]. Cette notion
permet de reformuler les équations de la physique, connues dans les référentiels
locaux X α, dans le système étendu x µ (cf.
calcul TENSORIEL). Par exemple, la loi de
conservation locale de l’énergie, qui s’écrit en chaque point :
µ qui
se réduit à la dérivation partielle usuelle ∂α = ∂/∂Xα dans
les référentiels localement inertiels [maintenant définis, de façon cohérente,
à partir de la structure riemannienne (6) comme les transformations X α = X α (x µ) qui réduisent,
autour d’un point donné x0, la forme (6) à la forme (5)
modulo des termes du second ordre
en X α
- X α(x
0)]. Cette notion
permet de reformuler les équations de la physique, connues dans les référentiels
locaux X α, dans le système étendu x µ (cf.
calcul TENSORIEL). Par exemple, la loi de
conservation locale de l’énergie, qui s’écrit en chaque point :
![]()
se réécrit comme :
![]()
où l’on a défini Tμν comme
le transformé tensoriel de Tab
:
![]()
![]()
sont les coefficients de Christoffel
, ou coefficients de connexion
, qui permettent de calculer la dérivation
covariante ![]() µ connaissant
le champ gμν(x ). Notons
au passage que le fait que l’opérateur de différentiation covariante fasse
intervenir, en plus des dérivées partielles, les quantités Γλμν, est analogue à l’apparition du terme supplémentaire
proportionnel au quadripotentiel électromagnétique dans l’opérateur de dérivation
µ connaissant
le champ gμν(x ). Notons
au passage que le fait que l’opérateur de différentiation covariante fasse
intervenir, en plus des dérivées partielles, les quantités Γλμν, est analogue à l’apparition du terme supplémentaire
proportionnel au quadripotentiel électromagnétique dans l’opérateur de dérivation
![]() µ
= ∂μ
- i. Aμ, qui est utilisé
pour coupler, de façon invariante de jauge, un champ chargé au champ électromagnétique.
Du point de vue mathématique, ce sont là deux exemples du concept géométrique général
de connexion linéaire (cf.
VARIÉTÉS DIFFÉRENTIABLES). Cela montre que, dès le niveau classique, il
y a un élément géométrique commun entre la relativité générale et les théories
de jauge (c’est-à-dire la théorie
de Maxwell et ses généralisations non linéaires ; cf. théorie des CHAMPS), lesquelles constituent, à l’heure actuelle,
le cadre général de description des interactions non gravitationnelles (électrofaibles
et fortes).
µ
= ∂μ
- i. Aμ, qui est utilisé
pour coupler, de façon invariante de jauge, un champ chargé au champ électromagnétique.
Du point de vue mathématique, ce sont là deux exemples du concept géométrique général
de connexion linéaire (cf.
VARIÉTÉS DIFFÉRENTIABLES). Cela montre que, dès le niveau classique, il
y a un élément géométrique commun entre la relativité générale et les théories
de jauge (c’est-à-dire la théorie
de Maxwell et ses généralisations non linéaires ; cf. théorie des CHAMPS), lesquelles constituent, à l’heure actuelle,
le cadre général de description des interactions non gravitationnelles (électrofaibles
et fortes).
Comme on le voit sur l’exemple de (8),
la reformulation des lois physiques dans un référentiel non inertiel étendu n’implique
que les quantités physiques transformées et le champ gμν(x ) [mais non les coefficients ∂Xα / ∂xμ]. L’équation
(8) montre aussi que, par rapport au référentiel étendu [x ], l’impulsion
de la matière n’est pas conservée (∂νTμν ≠
0) et
donc que l’on peut interpréter les Γλμν comme
des " forces accélératrices
" agissant sur la matière.
On en conclut que gμν est
lié aux effets physiques de la gravitation. Contient-il cette seule
information, et celle-ci est-elle exhaustive ? Le champ gμν contient
évidemment aussi une information sur le système de coordonnées, puisqu’il est
possible de transformer gμν sans
modifier le contenu des lois physiques, en changeant de référentiel. Quant à la
seconde question, elle est de nature expérimentale et peut être mise à l’épreuve
après déduction des équations qui déterminent gμν, une
fois leurs conséquences mises en évidence (cf. Équations de champ ). Les équations d’Einstein supposent que seul
gμν est
nécessaire et elles sont en accord, comme on va le voir, avec toutes les expériences
de gravitation réalisées jusqu’à présent. Les propriétés de l’espace-temps,
entièrement déterminées par gμν sont
établies par ces équations en fonction de la distribution de la matière dans l’Univers.
Équations de
champ
Einstein a cherché à généraliser l’équation
de Poisson, ΔU
= - 4πGρg , qui relie les dérivées secondes du potentiel newtonien U à la
densité de masse gravitationnelle ρg . La généralisation relativiste de ρg est, de façon essentiellement unique, le
tenseur d’énergie-impulsion Tμν à
cause, d’une part, des équivalences masse gravitationnelle = masse inertielle =
énergie/c², d’autre part, de l’absence
en relativité restreinte d’une description par un scalaire, ou un vecteur, de
la distribution d’énergie. Alors, comme le choix du référentiel étendu [x]
est complètement arbitraire, Einstein s’est
posé le problème de trouver un tenseur Sμν, formé à partir de gμν et
de ses dérivées, qui puisse être égalé à Tμν, ce qui implique, pour être cohérent avec (8),
que Sμν satisfasse
identiquement ![]() Sμν = 0. Dans un
espace-temps à quatre dimensions, ce problème a une solution unique
, à un facteur près, Sμν
= χ-2 Gμν[g ], si l’on impose : (a ) que Sμν dépend
au plus de gμν et
de ses dérivées premières et secondes ; (b ) que la géométrie minkowskienne gμν
= ημν est
une solution en absence de matière (Tμν = 0).
Sμν = 0. Dans un
espace-temps à quatre dimensions, ce problème a une solution unique
, à un facteur près, Sμν
= χ-2 Gμν[g ], si l’on impose : (a ) que Sμν dépend
au plus de gμν et
de ses dérivées premières et secondes ; (b ) que la géométrie minkowskienne gμν
= ημν est
une solution en absence de matière (Tμν = 0).
Cette solution unique conduit aux équations
d’Einstein (où le symbole
: = signifie " par
définition égal à ")
:
![]()
où Rμν : = Rαμαν et R
: = gμν Rμν sont
des contractions du tenseur de courbure :
![]()
(gμν est le tenseur inverse de gμν ; Tμν = g μρ g νσ
Tρσ ; on rappelle que le tenseur de courbure est nul si et seulement
si l’espace-temps est plat [minkowskien] ; cf. VARIÉTÉS
DIFFÉRENTIABLES). La constante
χ, dont le carré apparaît dans (10), est une
constante de couplage dimensionnée qui permet de relier Gμν et
Tμν (qui
ont des dimensions physiques différentes) et qui doit être déterminée expérimentalement
(cf. Approximations
postnewtoniennes et confirmations expérimentales ). Si l’on relâche certaines des conditions
imposées ci-dessus au tenseur Sμν , on
peut écrire des équations de champ plus générales que (10).
Par exemple, si l’on impose (a) mais
pas (b), la solution générale devient Sμν= χ-2 ( Gμν+ λ gμν) , qui contient une autre constante arbitraire,
la constante cosmologique λ (cf. COSMOLOGIE). Et, si l’on
admet la présence de dérivées d’ordre supérieur à 2, il devient
possible d’écrire des Sμν contenant beaucoup de constantes arbitraires et
faisant intervenir, par exemple, des termes non linéaires en Rαβμν. Il n’existe pas,
à l’heure actuelle, d’indications expérimentales suggérant l’emploi de telles généralisations;
cependant, les tentatives de quantification de la gravitation, et de son
unification avec les autres forces, prévoient de telles modifications aux très
courtes distances (cf. Relativité
générale, théorie quantique et unification).
Il est remarquable que, indépendamment
de l’approche " géométrique
" que nous venons de rappeler, les équations
de champ de la relativité générale puissent être élaborées également à partir
des aspects dynamiques du principe d’équivalence, de la manière selon laquelle
on formule une théorie de champ dans le cadre de la relativité restreinte.
Cette approche " dynamique
" fut élaborée, entre autres, par
Robert H. Kraichnan, Richard
P. Feynman, Steven Weinberg
et Stanley Deser. Son point de départ consiste à décrire l’interaction
gravitationnelle comme étant transportée par un champ h
qui se propage dans l’espace-temps
minkowskien. Alors, le fait expérimental de la déflexion de la lumière par le
Soleil suffit pour conclure que le champ h , s’il est supposé irréductible, doit être un
champ tensoriel de portée infinie (ou champ de spin
2 et de masse nulle). Mais, si, ensuite, par
analogie avec les équations de Maxwell :
![]()
qui couplent le champ Aµ à la distribution de charge et de courant décrite
par Jµ, on essaie de coupler le champ hμν à la distribution d’énergie et d’impulsion de
la matière décrite par le tenseur Tμν :
![]()
on aboutit à une incohérence. En
effet, les membres de gauche de (12) et (13) sont identiquement conservés, ce
qui entraîne nécessairement la conservation des membres de droite. Dans le cas électromagnétique,
on obtient ainsi ∂µJµ = 0, qui
est la loi de conservation de l’électricité. Mais, dans le cas gravitationnel,
on obtient ∂ν Tμν = 0,
c’est-à-dire la conservation locale de l’énergie et de l’impulsion de la matière,
ce qui est incompatible avec le fait que, à cause du terme de couplage, hμν Tμν, dans
le lagrangien dont dérive (13), on a nécessairement ∂ν Tμν ≠ 0,
puisque la matière échange de l’énergie et de l’impulsion avec le champ h
. Cette incohérence est alors résolue
en complétant la source Tμν par des termes
non linéaires en h qui décrivent le tenseur d’énergie-impulsion du champ h
lui-même. Ce procédé doit être itéré
jusqu’à atteindre une cohérence complète. Le résultat final redonne alors les équations
d’Einstein (10) si l’on identifie ημν
+ hμν avec gμν. Dans
cette approche, la non-linéarité des équations de champ (10) est donc
intimement liée avec la condition que pose le principe d’équivalence d’inclure
toutes les formes d’énergie dans la source de la gravitation, y compris l’énergie
due au champ gravitationnel lui-même. On trouve de même que la matière (y compris
tous les champs non gravitationnels) doit se coupler de façon universelle au
champ gravitationnel. Au niveau des équations d’évolution de la matière, cette
dernière condition se traduit par le fait que, partant des équations d’évolution
en relativité restreinte, on doit y remplacer partout ημν par gμν =
ημν+ hμν et les dérivées partielles par des dérivées
covariantes. Ce couplage universel au champ gravitationnel implique alors que
l’espace-temps plat de départ ημν devient
totalement inobservable, et que seul l’espace-temps riemannien gμν a un sens opérationnel.
Comme toutes les généralisations théoriques
en physique, qui, tout en transcendant les théories précédentes, s’y ramènent
dans les domaines où celles-ci demeurent valables, la relativité générale
comprend la théorie de la gravitation de Newton comme un cas limite
particulier. Explicitement, on s’attend que la limite newtonienne entre en jeu
lorsque le champ gravitationnel est faible et lentement variable, et lorsque la
source se meut lentement et ne possède que de faibles tensions internes. On
exprime mathématiquement cette situation par les conditions hμν << 1, ∂0h <<∂ih , T0i << T00 et Tij<< T00 ,
qui présupposent que l’on emploie un système de coordonnées adapté à cette
limite newtonienne (l’existence de telles coordonnées adaptées étant a
posteriori justifiée par la construction de solutions approchées).
On démontre d’abord, en utilisant l’équation
(8), qui exprime de façon covariante les équations du mouvement local de la
matière en présence de gravitation, et en considérant le cas limite d’une
distribution d’énergie concentrée en un point, qu’une particule d’épreuve se
meut sur une géodésique de l’espace de Riemann, soit :
![]()
où dτ² = -ds²/c² est
l’intervalle de temps propre. Pour de faibles vitesses et un champ
gravitationnel faible et lentement variable, cette équation se réduit, à l’ordre
le plus bas, à :
![]()
On doit donc identifier le potentiel
newtonien U avec c² h00/2.
Notons au passage que l’égalité
de m I
et mg s’est trouvée automatiquement incorporée dans l’équation
du mouvement d’une particule [au niveau exact (14), comme dans la limite
newtonienne (15)]. Contrairement à la théorie de Newton, en relativité générale
cette égalité découle de la structure même de la théorie puisque (14) se déduit
de (8) qui, elle-même, est une conséquence des équations de champ (10), puisque
![]() Gμν est
identiquement nul.
Gμν est
identiquement nul.
Reste à retrouver l’équation de
Poisson liant le potentiel newtonien à la densité de masse. D’abord, pour un
champ gravitationnel faible, on trouve que les équations d’Einstein (10) se réduisent
au premier ordre aux équations (13). Dans l’hypothèse supplémentaire d’un champ
lentement variable, ces dernières impliquent :
![]()
Si les pressions à l’intérieur de la
source sont faibles, ainsi que les vitesses, la " source " (T00 + Tii ) est dominée par
la densité de masse au repos ρc². On retrouve
donc l’équation de Poisson ΔU = - 4π Gρ, à
condition d’identifier la constante de couplage de la gravitation χ
à racine carrée de 8π
G/c4, où
G est la constante newtonienne de gravitation.
Approximations
post-newtoniennes et confirmations expérimentales
La très grande précision de certaines
mesures de distances et de durées actuellement réalisées dans le système
solaire nécessite de tenir compte très soigneusement des modifications que la
relativité générale apporte à la description newtonienne de l’espace-temps. Par
conséquent, la relativité générale est utilisée dans un grand nombre de
situations, depuis la recherche astronomique ou géophysique (interférométrie
radio à très longue base, poursuite radar des planètes, poursuite laser de la
Lune ou de satellites artificiels), en passant par les applications métrologiques
ou géodésiques (définition du temps atomique international, cartographie de précision),
jusqu’au vaste spectre d’applications pratiques des systèmes de positionnement
global par satellites (G.P.S.), allant de la construction du tunnel sous la
Manche aux systèmes de navigation maritimes, aériens, ou même automobiles
! Pour ce faire, une méthode d’approximation,
dite postnewtonienne , a été
développée qui consiste à compléter la limite newtonienne esquissée ci-dessus
en gardant les termes d’ordre supérieur dans le petit paramètre :
![]()
La description relativiste approchée
ainsi obtenue est ensuite utilisée pour ajuster de façon globale un très grand nombre de mesures. Ce caractère
global rend caduque la distinction traditionnelle de certains "
tests classiques " de la relativité générale (comme la déflexion
de la lumière ou l’avance relativiste des périhélies). Il est aujourd’hui plus
approprié de distinguer, au sein de l’ajustement global entre la théorie et l’expérience,
des effets physiques typiquement relativistes en utilisant une paramétrisation
adéquate de la métrique postnewtonienne.
Ce procédé de paramétrisation postnewtonienne (introduit par Arthur S.
Eddington dès 1923 et généralisé à la fin
des années 1960 par Kenneth Nordtvedt et Clifford M. Will) permet aussi de comparer les données expérimentales
brutes avec les prédictions faites par d’autres théories relativistes de la
gravitation qui ont été proposées comme alternatives à la relativité générale.
Par exemple, la relativité générale prévoit que l’écart hij=gij - δij entre la métrique d’espace et la métrique
euclidienne vaut (dans un système de coordonnées adéquat) 2U δij /c², alors que d’autres
théories prévoient pour hij une expression de même type mais affectée en général
d’un coefficient différent de 2. On utilise alors hij =2γU δij /c² où on laisse
libre le paramètre γ qui sera ajusté
au même titre que les autres paramètres inconnus lors de la comparaison globale
entre théories et expérience. Parmi la dizaine de paramètres postnewtoniens que
l’on peut ainsi introduire, deux jouent un rôle clé : γ, que
l’on vient d’introduire, et le paramètre β, qui
mesure certaines des non-linéarités de la gravitation relativiste, c’est-à-dire,
physiquement, le fait que l’énergie du champ gravitationnel est elle-même
source de gravitation (β = γ = 1 en relativité générale). Un autre paramètre ξ mesure
l’impossibilité de découpler le système solaire du champ gravitationnel crée
par la galaxie ( ξ = 0 en relativité générale, où
ce découplage est possible). Notons que les égalités ξ=0
et β=1 expriment chacune
un des aspects que prend le principe d’équivalence en relativité générale.
Le
caractère privilégié de γ et β vient
de ce qu’ils paramétrisent complètement le régime postnewtonien des
alternatives les plus simples à la relativité générale : les théories tenseur-scalaires de la
gravitation. Dans ces théories, l’interaction gravitationnelle est transportée
par deux champs à la fois : un
champ tensoriel (spin 2) de masse nulle
hμν couplé
à Tμν, et
un champ scalaire (spin 0) de masse nulle Φ
couplé à la trace Tαα.
Toutes les expériences réalisées à ce
jour dans le système solaire ont permis de déterminer, avec une précision
atteignant le millième, les valeurs des paramètres postnewtoniens.
Par exemple l’analyse de variations de
la gravité à la surface de la Terre a donné | ξ| < 10-3. Citons en particulier la mesure du retard,
causé par le champ gravitationnel du Soleil, dans les échos radars sur la
station Viking posée sur Mars, l’analyse globale de la dynamique du système
solaire (incluant l’avance des périhélies planétaires), et la mesure très fine
du mouvement relatif Terre-Lune obtenue à partir d’échos lasers sur les réflecteurs
déposés sur la Lune. Le résultat global donne :
![]()
Notons au passage que la déflexion des
rayons lumineux par le Soleil est proportionnelle à (1+ γ)/2 et permet donc de déterminer directement le paramètre γ. Mais
la précision ainsi obtenue, même avec les meilleures techniques modernes
utilisant des ondes radio, est seulement de l’ordre de 2 p.
100. Une
telle précision est cependant suffisante pour déterminer, comme on y a fait
allusion ci-dessus, que le champ qui propage l’interaction gravitationnelle à l’approximation
linéarisée doit être de spin 2 et de masse nulle, si l’on suppose qu’il est irréductible. Tous les résultats ainsi
obtenus sont compatibles avec la relativité générale (où ξ
= β - 1 = γ - 1 = 0), et en
constituent donc une excellente confirmation quantitative , au niveau de précision du millième. De plus,
toute théorie alternative de la gravitation est fortement contrainte. Par
exemple, dans les théories tenseur-scalaires le coefficient de couplage du
champ scalaire à la matière doit être mille fois plus petit que celui du champ
tensoriel einsteinien. Cependant, au niveau qualitatif, les expériences dans le
système solaire n’explorent qu’un petit domaine de l’ensemble des
manifestations de la gravitation :
celui des champs gravitationnels faibles et quasi stationnaires. Des
confirmations plus profondes de la relativité générale viendront de l’exploration
des autres domaines de manifestation de la gravitation, notamment des champs
gravitationnels forts et/ou rapidement variables. Nous ne discuterons pas ici
les aspects cosmologiques de la gravitation relativiste (cf.
COSMOLOGIE).
Champs
gravitationnels forts. Trous noirs
Le régime des champs gravitationnels
forts se rencontre dans la physique des corps gravitationnellement condensés.
Cette dénomination désigne les états
finals de l’évolution des étoiles. Après épuisement de leurs sources d’énergie
nucléaire, les étoiles finissent par condenser une masse énorme dans un rayon
très petit, conduisant, selon la masse initiale, à une naine blanche, à une étoile
à neutrons ou à un trou noir (cf. ÉTOILES et GRAVI-
TATION - Gravitation et astrophysique). Particulièrement
importante est l’existence d’une borne supérieure à la masse d’une naine
blanche ou d’une étoile à neutrons (cette borne supérieure ayant une origine
profonde dans la théorie quantique – principe de Pauli –
et dans la relativité restreinte – "
adoucissement " de l’équation d’état d’un gaz ultra relativiste).
Alors, quand une étoile froide excède cette borne supérieure (de l’ordre de
deux fois la masse du Soleil), rien ne peut l’empêcher de s’effondrer complètement
sur elle-même. Ce processus catastrophique conduit très vraisemblablement à la
formation d’un trou noir , c’est-à-dire
une structure particulière d’espace-temps courbe caractérisée par l’existence d’une
frontière (dite " horizon
" ou surface du trou noir) entre une
région extérieure, d’où il est possible d’émettre des signaux à l’infini, et
une région intérieure, où tout signal émis reste piégé (fig. 1). Notons que le développement temporel de la
région intérieure est limité, se terminant par une singularité où la courbure
devient infinie et où la description classique de l’espace et du temps perd son
sens. L’apparition d’une singularité associée à des régions de champ
gravitationnel fort est d’ailleurs un phénomène générique de la théorie d’Einstein,
comme le montrent des théorèmes dus à Roger Penrose et Stephen W.
Hawking. Dans le cas de la formation d’un
trou noir, cette singularité n’est pas " visible " de l’extérieur. La conjecture de " censure cosmique ", due à Penrose, affirme que le processus
d’effondrement d’un amas de matière conduit toujours à une telle singularité
" cachée ".
Les trous noirs ont
des propriétés remarquables. En particulier, un trou noir stationnaire isolé
est complètement décrit par trois paramètres (sa masse M, son moment cinétique J
: = Ma , et sa charge électrique Q) satisfaisant l’inégalité M²>
a² + Q², en unités où G = c = 1 ; il s’agit du " théorème
d’unicité " dû à Werner
Israel, Brandon Carter, David C. Robinson, Gary Bunting et Pawel O. Mazur. La géométrie d’espace-temps à l’extérieur
d’un tel trou noir est donnée par :
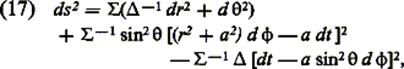
où D
= r² - 2Mr
+ a² + Q² et S
= r² + a² cos²q. La surface de ce
trou noir est située en r = r+ = M
+ (M²- a²- Q² )1/2. Cette
valeur de r apparaît comme singulière dans (17) puisque D s’y annule, mais la géométrie est pourtant
tout à fait régulière en r = r +, cette
singularité apparente provient du caractère inadéquat du système de coordonnées
r, q, f, t quand r tend vers r+. Cette
inadéquation n’est d’ailleurs pas accidentelle (et due par exemple à un mauvais
choix de la coordonnée radiale r) mais correspond à une caractéristique
physique fondamentale des trous noirs.
En effet, si la région
extérieure à un trou noir est bien stationnaire au sens usuel (c’est-à-dire
admet un groupe d’invariance de la métrique correspondant à des translations
" dans le temps
"), la région intérieure, quant à
elle, admet (par prolongement) un groupe d’invariance de la métrique, mais ce groupe
y correspond maintenant à des translations " dans l’espace " (ce qui veut dire que la région intérieure
est homogène mais non stationnaire). Ce changement profond de caractère de la
symétrie temporelle de l’espace-temps à la traversée de l’hypersurface r
= r +, et le fait que
cette dernière est une membrane unidirectionnelle que l’on ne peut traverser
que dans un sens, a été d’abord clairement reconnu à la fin des années 1950, grâce
notamment aux travaux de David Finkelstein, Christian Fronsdal et Martin
Kruskal, sur le cas particulier a = Q = 0 de (17), c’est-à-dire
sur la métrique dont la forme extérieure (trouvée par Karl Schwarzschild dès
1916) est :
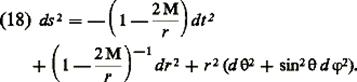
Le caractère régulier de l’horizon r
= 2M de (18) se vérifie
par exemple en introduisant (à l’extérieur r
> 2M,
puis en prolongeant aux r < 2M) les nouvelles
coordonnées :
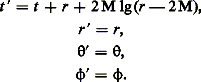
D’un intérêt particulier est aussi la
région (dite " ergosphère
") comprise entre r
= r + et
r = M
+ (M2 - a² cos²q - Q²)1/2. Dans cette région
(qui n’existe que si a > 0, c’est-à-dire
pour un trou noir " tournant
"), les effets de type "
magnétique " de la gravitation du trou noir
(initialement créés par les courants de matière dans l’étoile en rotation qui s’est
effondrée) sont si intenses qu’ils entraînent nécessairement, tel un maelström,
tout corps qui y pénètre dans un mouvement de rotation autour du trou noir.
Dans cette région encore, il est possible pour une particule tombant depuis l’infini
de s’y désintégrer de telle sorte que l’un de ses fragments reparte à l’infini
en emportant plus d’énergie que la particule incidente. Ce phénomène
remarquable (d’abord noté par Penrose) montre qu’un trou noir est non seulement
un puits de potentiel gravitationnel mais aussi un objet physique possédant une
énergie libre importante qu’il est possible, en principe, d’extraire. L’énergétique
des trous noirs est résumée dans leur " formule de masse " (due à Demetrios Christodoulou et Remo
Ruffini) :
![]()
où Mirr désigne
la masse irréductible du
trou noir, une quantité qui ne peut qu’augmenter de manière irréversible. Comme
l’aire totale de la surface du trou noir (laquelle a la topologie d’une sphère)
vaut A = 16p
M²irr, l’irréversibilité
fondamentale de l’évolution d’un trou noir peut encore s’exprimer en disant que
A ne peut que croître (théorème de Hawking). Ce résultat a suggéré à Jacob D.
Bekenstein d’interpréter l’aire de l’horizon,
A, comme étant proportionnelle à l’" entropie "
du trou noir. Une telle interprétation thermodynamique est renforcée par l’étude
de l’accroissement de A sous l’influence de perturbations externes, accroissement
que l’on peut en effet attribuer à des propriétés dissipatives locales de la
surface du trou noir :
notamment une viscosité surfacique et une résistivité électrique surfacique
(égale à 377 ohms). Ces interprétations " thermodynamiques "
des propriétés des trous noirs restent de simples analogies au niveau de la
physique classique, mais un résultat remarquable de Hawking a montré qu’elles
avaient un contenu réel au niveau de la physique quantique. En 1974, Hawking a étudié
l’aspect le plus simple de l’interaction entre la gravité et la théorie
quantique, le comportement d’un champ quantique se propageant dans l’espace-temps
classique de fond d’un trou noir. Il a trouvé que la présence d’un horizon,
au-delà duquel la géométrie d’espace-temps n’est plus stationnaire au vrai sens
du terme, avait des conséquences importantes pour la notion de particule
quantique. Il trouva en particulier qu’un trou noir devait émettre de façon
continue un flux de particules ayant le spectre caractéristique (spectre de
Planck pour les bosons de masse nulle) d’une émission thermique de température T
= 4h ∂M / ∂A. À une telle
" température d’émission
du trou noir "
correspond, par la relation thermodynamique T = ∂E / ∂S, une entropie
S =
A / (4h ). Ce résultat
confirme la réalité du concept d’entropie d’un trou noir et révèle une
connexion inattendue – et
peut-être profonde – entre
gravitation, thermodynamique et théorie quantique.
Signalons enfin, en revenant au niveau
classique, que la formule de masse (19) montre que les trous noirs sont les
plus grands réservoirs d’énergie libre de l’Univers, puisque 29 p.
100 de leur énergie de masse peut être stockée
sous forme de rotation, et même 50 p. 100 sous forme d’énergie électrique (on comparera ces valeurs aux
quelques pour-cent d’énergie de liaison nucléaire qui correspondent pourtant à
toute la lumière émise par les étoiles pendant leur vie). Cela suggère que les
trous noirs peuvent constituer le moteur central de certains des phénomènes les
plus énergétiques de l’Univers, en particulier les quasars (cf. QUASARS).
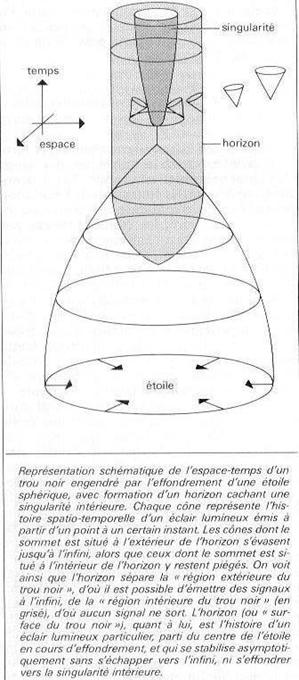
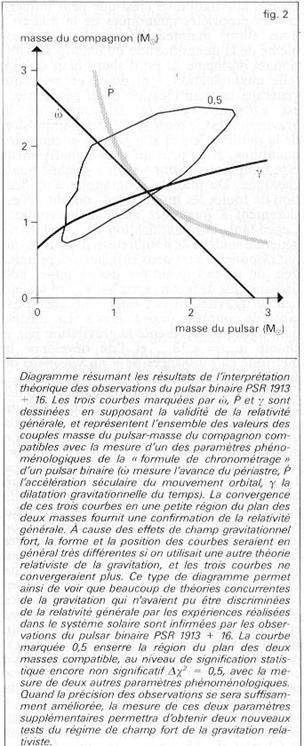
Figure 1 Figure
2
Un autre domaine de la relativité générale
qui suscite des recherches très actives, tant du point de vue théorique que du
point de vue expérimental, est celui des champs gravitationnels rapidement
variables, lesquels, une fois engendrés dans la source, s’en éloignent sous la
forme d’ondes gravitationnelles. D’où
trois problèmes séparés :
celui de la génération, celui de la propagation et, enfin, celui de la détection
du rayonnement gravitationnel. Dans le cas le plus simple d’ondes gravitationnelles
très faibles, considérées très loin de leur source, la géométrie d’espace-temps
associée peut s’écrire sous la forme gμν
= ημν
+ hμν , avec |
h μν
| <<
1. Alors,
les équations de propagation de
hμν
sont
données (à l’ordre linéarisé) par l’équation (13), où l’on remplace le membre
de droite par zéro. Dans un système de coordonnées adéquat, de telles ondes
gravitationnelles satisfont h00TT = 0 = h0i TT et
:
![]()
ce qui veut dire que ce sont, à l’instar
des ondes électromagnétiques, des ondes transverses et sans traces (TT), décrites par deux polarisations indépendantes
dans le plan orthogonal à la direction de propagation, et qui se propagent à la
vitesse c , comme le montre
la présence du d’alembertien □ : = ∆- c²∂²/∂t², dans les équations
(20).
Le problème de la génération
consiste à chercher le lien entre l’amplitude
tensorielle hijTT du rayonnement gravitationnel dans la zone d’ondes,
et le mouvement et la structure de la source. Si l’on considère le cas le plus
simple d’une source suffisamment peu condensée pour n’engendrer que des ondes
partout faibles (hμν << 1), on peut
utiliser l’approximation linéarisée des équations d’Einstein (10), c’est-à-dire
(13). Si l’on choisit un système de coordonnées tel que ∂αhαμ
– (∂μhαα /2)
= 0, on trouve que
hμν est donné par :
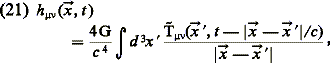
où![]() = Tμν - 1/2 ημν Tαα. La formule (21), qui décrit comment une
source faible Tμν engendre le champ hμν ,
est l’analogue gravitationnel de la génération d’un champ électromagnétique Aµ (en
jauge de Lorentz ∂αAα =
0) par sa source Jµ [cf. (12)] :
= Tμν - 1/2 ημν Tαα. La formule (21), qui décrit comment une
source faible Tμν engendre le champ hμν ,
est l’analogue gravitationnel de la génération d’un champ électromagnétique Aµ (en
jauge de Lorentz ∂αAα =
0) par sa source Jµ [cf. (12)] :
![]()
On trouve alors que, de même que la
conservation de la charge implique qu’il n’y a pas d’émission électrique de
type monopolaire, mais seulement dipolaire ou d’un ordre de polarité plus élevé,
de même la conservation de l’énergie-impulsion implique l’absence de
rayonnements gravitationnels monopolaires et dipolaires. Pour une source
lentement variable, le rayonnement gravitationnel dominant sera donc
quadrupolaire ; il est donné,
dans la zone d’ondes, par l’expression :
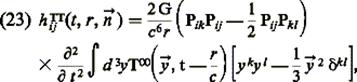
où Pij = δij - ninj est le projecteur dans le plan orthogonal à la
direction n de propagation. On montre que le résultat (23)
est encore valable pour une source lente et faiblement autogravitante, pour
laquelle on doit faire intervenir certains aspects non linéaires des équations
d’Einstein. Le cas, plus intéressant car plus efficace pour engendrer du
rayonnement, d’une source rapidement variable et fortement autogravitante,
donne lieu aujourd’hui à d’intensives études théoriques fondées en
partie sur l’utilisation de gros ordinateurs.
Enfin, le problème de la détection
, dont le pionnier fut Joseph Weber dans
les années soixante, suscite de nos jours de très actives recherches expérimentales.
Le principe de tous les détecteurs repose sur le fait qu’une onde
gravitationnelle d’amplitude h induit, lors de son passage, un déplacement de
l’ordre de δL ≈
h . L
entre deux corps distants de L. Le problème est donc de détecter
un très petit déplacement relatif δL/L ≈ h . Les détecteurs qui semblent aujourd’hui les plus prometteurs
sont de grands interféromètres, du type Michelson ou Fabry-Pérot, ayant des
bras kilométriques et dans lesquels est injecté un faisceau laser monochromatique
très puissant. De tels systèmes sont étudiés en Allemagne, en Australie, aux États-Unis,
en France, en Italie, au Japon et au Royaume-Uni. Deux projets de détecteurs
kilométriques ont été approuvés et sont en cours de construction : le projet américain L.I.G.O. (Laser
Interferometer Gravitational Wawe Observatory) et le projet Virgo
(collaboration France-Italie). Ils devraient mesurer des amplitudes h
aussi faibles que 10-22, et ainsi permettre de détecter le rayonnement gravitationnel émis
lors des étapes ultimes d’évolution de systèmes doubles d’étoiles à neutrons,
comme les pulsars binaires décrits ci-dessous, situés dans des galaxies
lointaines (jusqu’à 600 millions
d’années de lumière de nous). La détection des ondes gravitationnelles apportera
des renseignements inestimables pour l’astronomie en ouvrant une nouvelle
" fenêtre " sur l’Univers.
Pour conclure ce survol des aspects
classiques de la relativité générale, parlons brièvement des "
pulsars binaires ", c’est-à-dire des systèmes doubles
constitués d’un pulsar (étoile à neutrons en rotation rapide sur elle-même) et
d’une étoile compagnon très dense (étoile à neutrons ou naine blanche). Le
premier système de ce type, nommé PSR 1913 + 16,
a été découvert par Russell A. Hulse
et Joseph H. Taylor en 1974.
Grâce aux observations régulières réalisées par Joseph H. Taylor et ses collaborateurs depuis sa découverte,
il a été possible de suivre avec une précision remarquable le mouvement orbital
du pulsar. Ce qui rend ce système si intéressant du point de vue théorique, c’est
qu’il contient des régions où le champ gravitationnel est très intense. En
effet, la courbure de l’espace-temps à l’intérieur et au voisinage immédiat du
corps gravitationnellement condensé qu’est le pulsar (et sans doute aussi
son compagnon) est grande (avec | hμν | de l’ordre de 0,40, au lieu de 10-6 dans le système solaire). De plus, le fait que l’interaction gravitationnelle se propage à
la vitesse de la lumière entre le pulsar et son compagnon joue un rôle
important. L’étude théorique de ce système a nécessité le développement d’une
nouvelle méthode capable de tenir compte de la présence de régions de champ
fort, et de traiter avec soin le phénomène de propagation de l’interaction
gravitationnelle. Cette méthode a d’abord permis de démontrer que, en relativité
générale, tous les effets de champ gravitationnel fort pouvaient être absorbés
dans la définition d’une " masse
observable " pour
chaque objet. Cette propriété, qui est encore un des aspects du principe d’équivalence,
est caractéristique de la relativité générale et n’est pas vraie dans les
autres théories de la gravitation (notamment les théories tenseur-scalaires où
les effets de champ gravitationnel fort peuvent introduire d’importantes
modifications dans l’interaction gravitationnelle de deux étoiles à neutrons).
On voit là comment les mesures faites sur les pulsars binaires permettent d’aller
au-delà des expériences effectuées dans le système solaire en sondant le régime
des champs gravitationnels forts. Pour ce faire, il faut pouvoir effectuer une
comparaison détaillée entre les données observationnelles brutes (qui
consistent en une série discrète de temps d’arrivée sur Terre des impulsions électromagnétiques
en provenance du pulsar en mouvement orbital) et une classe générale de théories
de la gravitation. De façon un peu similaire à ce qui a été dit plus haut à
propos des tests dans le système solaire, une telle comparaison est possible
par un processus de paramétrisation appelé " postképlérien ". Mais, dans ce cas, ce n’est pas la métrique
d’espace-temps que l’on paramétrise, mais directement la " formule de chronométrage " qui donne les temps d’arrivée théoriques
des signaux sur Terre en fonction d’une vingtaine de " paramètres phénoménologiques ". On obtient alors des tests de la
relativité générale (ainsi que d’une large classe d’autres théories de la
gravitation) si l’on mesure plus de paramètres phénoménologiques que le nombre
minimal de paramètres dynamiques qui suffisent à caractériser intrinsèquement
le système. Dans le cas du système PSR 1913 + 16,
il a été possible de mesurer trois paramètres phénoménologiques orbitaux (ou
paramètres postképlériens) :
ω, qui mesure l’avance
du périastre, γ (à ne pas confondre avec le paramètre
postnewtonien introduit ci-dessus), qui mesure la dilatation gravitationnelle
de la fréquence de rotation du pulsar sur lui-même, et P,
qui mesure la variation séculaire de la période orbitale. La physique des
champs gravitationnels intenses entre dans la détermination de ω,
γ et P.
De plus, l’origine physique de P peut être directement attribuée au fait que l’interaction
gravitationnelle entre le pulsar et son compagnon se propage à la vitesse de la
lumière (cf. équation 21).
Cette propagation à vitesse finie produit, dans la force gravitationnelle
agissant sur le pulsar, une composante opposée à sa vitesse orbitale qui fait
progressivement " tomber
" le pulsar sur une orbite plus
basse autour de son compagnon, causant ainsi une diminution progressive de la période
orbitale (P S 0).
Notons que, dans quelque 300 millions
d’années, cette " chute
" progressive du pulsar et de son
compagnon l’un vers l’autre conduira à un système binaire extrêmement serré, en
mouvement spiral convergent, émettant, lors des derniers milliers d’orbites, un
rayonnement gravitationnel très intense qui est le prototype des sources d’ondes
gravitationnelles que les projets L.I.G.O. et Virgo
cherchent à détecter dans d’autres galaxies. La mesure simultanée de ω,
γ, et P
dans PSR 1913 +
16 donne lieu à un test combiné du régime de
champ fort et des propriétés de propagation de la gravitation (fig.
2). La relativité générale passe ce test
avec une précision de 3,5. 10-3.
Un autre pulsar binaire, PSR
1534 + 12,
découvert par Aleksander Wolszczan en 1991, a permis quant à lui de mesurer
cinq paramètres postképlériens :
ω, γ et
P et deux nouveaux paramètres r et s, qui
mesurent l’amplitude et la forme du retard gravitationnel des signaux du pulsar
causé par la présence du compagnon. Ces cinq mesures simultanées donnent lieu à
deux tests " purs
" du régime de champ fort, et un
test combiné du régime de champ fort et des aspects radiatifs de la
gravitation. Là encore, la relativité générale passe ces trois nouveaux tests
avec un complet succès.
En conclusion, l’étude des pulsars
binaires a permis de confirmer pour la première fois que la théorie d’Einstein
décrit correctement le régime des champs gravitationnels intenses, et de
prouver observationnellement que l’interaction gravitationnelle se propage à
vitesse finie (ce qui démontre la réalité des ondes gravitationnelles).
4.
Relativité générale, théorie quantique et unification
Nous n’avons jusqu’ici examiné que la
relativité générale classique, qui est pertinente pour décrire la gravitation à
l’échelle macroscopique, mais insuffisante pour étudier l’interaction
gravitationnelle à l’échelle microscopique, où entre en jeu le caractère
quantique des particules élémentaires. Nous avons déjà noté, à propos de la radiation
thermique des trous noirs de Hawking, qu’un champ gravitationnel classique peut
influencer les propriétés quantiques de la matière ; nous allons maintenant considérer le problème
de la quantification du champ gravitationnel lui-même. Il est d’abord clair qu’une
telle quantification – et
donc, en relativité générale, la quantification de la géométrie – est nécessaire puisque la source de la
gravitation est le tenseur d’énergie-impulsion de la matière, lequel a, a
priori, un caractère quantique, et ne peut qu’approximativement être remplacé
par une valeur moyenne quasi classique. De plus, le programme d’unification de
toutes les interactions conduit nécessairement à quantifier aussi la
gravitation. Cependant, la quantification de la relativité générale soulève de
nombreuses difficultés qui ont essentiellement deux origines : en premier lieu, on ne sait quantifier des
systèmes non linéaires que de façon perturbative; en second lieu, la
gravitation fait intervenir une constante de couplage dimensionnée. En théorie
quantique, on représente la gravitation par le champ φμν
= χ -1
hμν ,
et l’on développe la métrique en puissances de χ au voisinage de sa valeur minkowskienne
: g μν = ημν
+ χφμν. Or,
comme l’avait remarqué Planck, immédiatement après la découverte du quantum d’action
(constante de Planck = 2 πh ), la
quantité l0 = χ(hc /8 π)1/2 a
la dimension d’une longueur ( l0 ≈ 1,6.10 -33 cm, correspondant à une énergie E0 = hc /l
0
≈ 1,2.1028
eV). Mais
une théorie de champ quantique faisant intervenir une constante de couplage
ayant la dimension d’une longueur n’est pas renormalisable, ce qui veut dire
que le calcul des effets quantiques non linéaires fait apparaître des quantités
infinies qui enlèvent tout caractère prédictif à cette théorie au-delà de l’ordre
linéaire (lequel reste une théorie bien définie de particules quantiques libres
: " gravitons " de spin 2
et de masse nulle dans le cas gravitationnel). En outre, l’invariance de la
relativité générale par rapport à toutes les transformations de coordonnées
(qui est analogue à l’invariance de jauge des théories de jauge) implique la présence
de contraintes compliquées entre les variables de champ. Les travaux de Paul
Dirac et de Richard Arnowitt, Stanley Deser et Charles W. Misner ont cependant permis de construire une
formulation hamiltonienne de la relativité générale classique, mais la
quantification de cette dernière est loin d’être évidente. D’autres tentatives
de quantification ont été faites (par exemple les formulations "
covariantes de Lorentz ", étudiées en particulier par Bryce S.
DeWitt), mais elles se sont toutes heurtées
à de graves difficultés. En somme, la quantification directe de la théorie d’Einstein
pose problème. Peut-être faut-il alors considérer que la relativité générale n’est
pas une théorie fondamentale, mais seulement une théorie effective qui découle,
comme approximation macroscopique, d’une théorie unifiée sous-jacente. Cette
ambitieuse vision unificatrice est devenue dominante depuis le début des années
soixante-dix, après le succès de l’unification des forces non
gravitationnelles, sous l’influence conjuguée de nouvelles idées (supersymétrie,
cordes) et de l’idée plus ancienne (due à Theodor Kaluza et Oskar Klein) que l’espace-temps
a peut-être plus de quatre dimensions.
Historiquement, les premières
tentatives d’unification ne comprenaient que la relativité générale et l’électromagnétisme,
décrit par le quadripotentiel Aµ. Kaluza
et Klein réalisèrent que les champs gμν et Aµ, qui
apparaissent séparés dans l’espace-temps à quatre dimensions (D
= 4),
pouvaient être unifiés dans la métrique riemannienne d’un espace-temps à cinq
dimensions (D = 5) : gMN = (gμν ,
gµ5, g55) ;
ce procédé fait apparaître un
champ scalaire supplémentaire en D = 4. Afin d’expliquer
pourquoi on ne voit pas la cinquième dimension, on peut alors supposer qu’elle
se referme sur elle-même en cercles de rayon ≈
l0. Une
telle périodicité par rapport à la cinquième dimension permettrait aussi d’expliquer
la quantification de la charge électrique. (Ces idées peuvent se généraliser à
l’unification de la relativité générale avec les théories de jauge non abéliennes
de Yang-Mills.) De telles tentatives d’unification " géométrique " furent abandonnées (sauf par Einstein
lui-même) quand furent découvertes de plus en plus de particules "
élémentaires ", comprenant notamment des particules de
spin 1/2 (électron, neutrino, quark...) qui sont décrites par des champs fermioniques
de nature essentiellement quantique, sans analogues classiques. À la place fut
entrepris un programme d’unification " dynamique " des interactions non gravitationnelles qui conduisit à la
théorie électrofaible, à la chromodynamique quantique (théorie des interactions
fortes), ainsi qu’aux essais de " grande unification ".
Toutes ces théories représentent les interactions comme dues à l’échange de
particules bosoniques de jauge. En 1974, après en particulier un travail de
Julius Wess et Bruno Zumino, la supersymétrie , c’est-à-dire une sorte de rotation globale
transformant les bosons en fermions et réciproquement, permit de
concevoir une unification plus profonde entre champs bosoniques (interactions)
et champs fermioniques (matière). Assez rapidement, la supersymétrie globale
fut généralisée à une supersymétrie locale, ce qui conduisit à la théorie de la
supergravité, découverte en 1976 par Daniel Z. Freedman, Peter Van Nieuwenhuizen et Sergio
Ferrara, et par Stanley Deser et Bruno Zumino. Cette théorie unifie la relativité
générale dans un supermultiplet de jauge contenant, en plus du graviton, un
fermion sans masse, de spin 3/2. La supergravité fut étendue à d’autres multiplets et fut formulée
dans des espaces-temps ayant plus de quatre dimensions (notamment D
= 10 et 11). Mais, comme ces théories contiennent toujours la constante de
couplage dimensionnée χ, elles restent
non renormalisables, et le seul espoir de leur donner un sens au niveau
quantique est que les interactions non linéaires infinies entre bosons puissent
être compensées par les interactions (également infinies, mais en général de
signes opposés) entre fermions. Malheureusement, bien que de telles
compensations existent pour les premiers ordres d’interaction non linéaire, on
s’aperçut rapidement que ce n’allait probablement pas être le cas pour les
ordres élevés d’interaction (la vérification explicite de ce fait est cependant
si ardue qu’elle semble impossible sans le recours à de puissants ordinateurs,
comme cela a été fait pour le calcul des termes infinis du deuxième ordre d’approximation
de la gravitation quantique).
Pendant ce temps, pour des raisons
tout à fait différentes (et qui restent en grande partie mystérieuses), les théories
des cordes commencèrent à manifester une affinité avec la gravitation.
Initialement formulées (notamment par Gabriele Veneziano, Yoshiro Nambu et T.
Goto) comme modèles des interactions
fortes, les théories des cordes, fondées sur la quantification de la dynamique
relativiste d’un objet étendu selon une dimension spatiale, montrèrent deux
propriétés remarquables : une
grande unicité (même la dimension de l’espace-temps où elles sont formulées est
fixée) et la présence d’excitations quantiques ayant les propriétés du graviton
(Joël Scherk et John H. Schwarz, et Tamiaki Yonea, 1974). Une troisième propriété remarquable (possibilité
naturelle de l’absence d’" anomalies
quantiques " des
invariances de jauge) stimula, après sa découverte, par Michael B.
Green et John H. Schwarz, à l’automne de 1984, une intense
recherche sur les théories de cordes. Comme ces théories incluent non seulement
la gravitation mais aussi des champs de jauge et des fermions, et qu’il semble
qu’elles donnent lieu, à tous les ordres de non-linéarité, à des interactions
finies, elles apparaissent comme d’intéressants candidats pour réaliser le
programme d’unification de toutes les forces. De plus, elles ne contiennent qu’un
seul paramètre ajustable, ayant la dimension d’une longueur au carré, qui est
relié à l²0.
Avant cependant de pouvoir comparer les théories des cordes à l’expérience,
deux problèmes fondamentaux doivent être résolus. Le premier est celui de la
" compactification
" : comment se fait-il que, parmi les dix (par
exemple) dimensions des espaces-temps où sont définies certaines de ces théories,
six se referment sur elles-mêmes sur des distances très courtes pour ne laisser
que quatre dimensions apparentes ?
Le second est celui de la " brisure
de symétrie " : comment les particules originairement sans
masse de ces théories engendrent-elles les particules massives que l’on observe
? Lié à ce deuxième problème est celui de
la constante cosmologique Λ : comment se fait-il que la gravitation
macroscopique ne fasse pas intervenir de terme en Λ dans les équations d’Einstein (ou tout au
moins un terme extrêmement petit, s’il existe ; l’expérience indiquant que Λ
< 6 . 10-56 cm-2)
alors que la brisure de symétrie engendre en général un Λ quelque
120 ordres de grandeur plus
grand (Λ ≈ l0 -2 ≈ 4.10 65 cm-2) ! Ce dernier problème est central dans tout essai de
quantification de la gravitation couplée à la matière, et suscite actuellement
d’intenses recherches.
Esquissons maintenant brièvement la
structure des théories de supergravité et des cordes. La supergravité peut être
motivée, d’une tout autre façon que via le concept de supersymétrie, en se
posant le problème de coupler à la gravité, de façon cohérente, des champs de
jauge de spin strictement plus grand que 1 (notamment s
= 3/2). En absence de
gravité, c’est-à-dire dans l’espace-temps plat de Minkowski, l’équation de
propagation d’un champ de spin 3/2, décrit par un vecteur-spineur
réel ψµ, est
:
![]()
où ε est
le symbole totalement antisymétrique de Levi-Civita, et où les γ désignent
les matrices de Dirac. Cette équation de propagation satisfait clairement l’identité
∂μRμ ≡ 0, laquelle est nécessaire
à la cohérence de la théorie d’un champ de spin 3/2. En présence
de gravité maintenant, c’est-à-dire dans un espace-temps courbe, on peut
toujours introduire la notion de champ de vecteurs-spineurs ψµ à
condition d’utiliser en chaque point un repère orthonormé. Introduisant alors l’opérateur
de dérivation covariante d’un spineur ▼µ [qui
fait intervenir les coefficients de la connexion linéaire par rapport au champ
de repères orthonormés, et non plus simplement les coefficients (9) qui correspondaient au champ de repères
affines associé à un système de coordonnées], on écrira pour la propagation de
ψµ :
![]()
Mais, alors, la non-commutativité des
dérivées covariantes (qui est l’indice de la présence d’une courbure) fait que
l’équation ▼μRμ =
0, nécessaire à la cohérence n’est plus satisfaite
identiquement mais implique la contrainte suivante sur le tenseur d’Einstein
: Gμνγμψν = 0. En général,
cette contrainte ne peut être satisfaite que dans le vide (Gμν
= 0)
et semble donc incompatible avec le fait que le tenseur d’énergie-impulsion du
champ ψ, Tμν(ψ), soit une source
du champ gravitationnel [Gμν
= χ²
Tμν(ψ)]. Cependant, la
supergravité arrive à éviter cet écueil, grâce notamment aux propriétés d’anticommutation
des champs spinoriels quantiques qui permettent d’avoir identiquement Tμν(ψ) γμψν ≡0. De plus, un tel
lien de cohérence entre les équations de propagation du vecteur-spineur et de
la gravité signifie qu’il existe une nouvelle invariance locale de la théorie,
associée à un paramètre fermionique α(x ) qui
transforme simultanément en chaque point ψ et
γ :
![]()
Cette invariance locale (c’est-à-dire
différente d’un point à l’autre) généralise l’invariance globale (la même en
chaque point) de supersymétrie qui existe en espace-temps plat. La supergravité,
par le point de vue plus général qu’elle apporte, a permis de découvrir des
propriétés nouvelles de la relativité générale classique. En particulier, à peu
près au même sens où l’équation de Dirac a montré que l’équation des ondes était
le " carré
" d’une autre équation, la
supergravité a montré qu’un déplacement dans l’espace-temps pouvait être écrit
comme le produit de deux transformations de supersymétrie, ce qui implique que
l’énergie totale d’un système gravitant était un carré (E
= Q², où Q
est une " supercharge
" conservée associée à la
superinvariance). Ce résultat
a indiqué une voie pour démontrer que l’énergie totale d’un système
autogravitant était toujours non négative (et nulle seulement pour l’espace-temps
plat), une propriété fondamentale pour la stabilité de la relativité générale
classique. La supergravité " simple
" que nous venons d’esquisser a été
" étendue " dans plusieurs directions : plus de champs, plus de supersymétries, plus
de dimensions d’espace-temps. Toutes ces extensions ont des limitations
naturelles : il ne peut pas
y avoir de champs de spin supérieur à celui du graviton (ce qui est en accord
avec l’expérience), et il n’est pas possible de dépasser onze dimensions d’espace-temps
(cette dernière dimension n’admettant plus qu’une seule supersymétrie).
Malgré leur élégance et leurs
remarquables propriétés géométriques, les théories de supergravité ne semblent
pas physiquement viables, car elles ne sont pas renormalisables. C’est là un
problème que la théorie des cordes semble éviter de façon radicale en
quantifiant non plus des particules ponctuelles (qui donnent lieu à des champs
quantifiés), mais des " cordes
", c’est-à-dire des objets étendus
dans une dimension spatiale, qui peuvent être " ouvertes " ou refermées sur elles-mêmes en boucles. La dynamique
relativiste classique d’un tel objet est définie en extrémisant l’aire de la
2-surface tracée dans l’espace-temps par le mouvement de la corde.
Ensuite, la quantification de cette dynamique classique fait apparaître des
propriétés nouvelles. D’abord, l’espace-temps de fond où est plongée la corde
doit avoir 26 dimensions pour
les théories originales des cordes dites " bosoniques ", et 10 pour les cordes " supersymétriques ". Ensuite, la quantification des modes de
vibration de la corde engendre un spectre infini de particules. En effet, à
chaque " instant
", la configuration de la corde
classique est décrite par des fonctions xμ (σ), exprimant les
coordonnées de chaque point de la corde en fonction d’une abscisse curviligne σ. La décomposition
de Fourier de xμ (σ) en sinus et
cosinus définit alors un ensemble discret d’amplitudes αμn (n=
0, + 1, + 2,...) qui, après
quantification, deviendront des opérateurs de création ou d’annihilation d’états
quantiques correspondant à des particules quantiques de spin et de masse déterminés.
Il se trouve (miraculeusement ?)
que l’exigence de cohérence quantique de la théorie implique nécessairement la
présence, entre autres, d’une particule sans masse de spin
2 dans les excitations quantiques des cordes
fermées, alors que les cordes ouvertes donnent lieu à une particule sans masse
de spin 1. De plus,
la théorie des cordes ouvertes contient nécessairement des cordes fermées (en
gros parce qu’elles peuvent toujours se refermer en joignant leurs extrémités).
Nous avons indiqué plus haut que toute théorie cohérente de particules sans
masse de spin 2
devait conduire à la relativité générale, ou à ses généralisations contenant
des termes non linéaires dans le tenseur de courbure (11). Et on peut en effet construire une théorie
effective classique de la gravitation en 26 dimensions engendrée
par la théorie quantique des cordes bosoniques qui contient la relativité générale
plus une série de corrections non linéaires du type l02n
(courbure)n . Les cordes
supersymétriques, les seules physiquement intéressantes car ne donnant probablement
lieu à aucun infini, engendrent quant à elles, à l’ordre le plus bas, la
supergravité en 10 dimensions. Ces
corrections d’origine quantique à la relativité générale sont, bien entendu, négligeables
à l’échelle macroscopique où l0 ² (courbure) ≈ [l0/ (longueur macroscopique)]² <<
1. Dans
cette approche, on voit que la relativité générale classique n’a pas à être
quantifiée, puisqu’elle émerge comme l’approximation effective classique d’une
théorie quantique des cordes.
En conclusion, quoi qu’il
advienne de l’espoir que les théories quantiques des cordes (ou d’autres objets
étendus) contiennent la clef du problème de l’unification des forces, l’étude
de ces théories a déjà élargi notre horizon et ne pourra que continuer à
enrichir notre compréhension du rôle de la relativité générale au sein de la
physique.