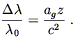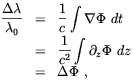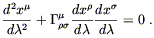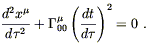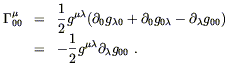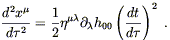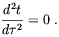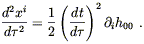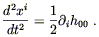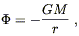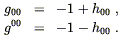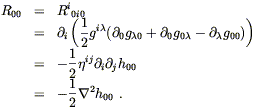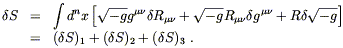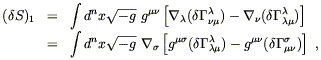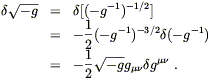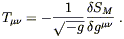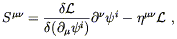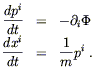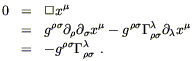lhttp://pancake.uchicago.edu/~carroll/notes/ : J. Fric endosse toute responsabilité pour les erreurs que sa traduction (qui n’a pas été vérifiée par l’auteur) aurait pu ajouter. En cas de doute, veuillez vous rapporter à la version originale.
Table des matières
Introduction 4
Principe d’équivalence 4
Principe d’équivalence faible 4
Principe d’équivalence d’Einstein 6
Principe d’équivalence fort 7
De la définition et de la mesure de l’accélération gravitationnelle 7
Définition du mouvement chute libre dans un champ gravitationnel 7
De la difficulté de construire un référentiel étendu à l’espace-temps entier en Relativité générale 8
Faute de mieux, construisons un référentiel local 8
Premières conséquences 8
La gravitation est la manifestation de la courbure de l’espace-temps 9
Décalage spectral comme conséquence directe du PEE 9
La courbure nécessaire de l’espace-temps 10
Un peu de formalisme mathématique 12
La courbure de l’espace-temps est suffisante 12
Limite Newtonienne 13
Vers les équations du champ 14
“Principe de covariance”: Comment les lois se conservent quand on passe d’un référentiel à un autre 15
Exemples pratiques d’application du principe de covariance 15
L’application du principe de covariance peut conduire à des ambiguïtés 16
Limites du principe d’équivalence 17
Exemple de l’introduction d’une constante de couplage entre champs 17
À l’échelle macroscopique la constante de couplage peut être négligée 18
Établissement de l’équation d’Einstein 18
Première méthode d’établissement des équations d’Einstein : par généralisation de l’équation de Poisson 18
La limite Newtonienne 20
L’équation d’Einstein 21
La signification de l’équation d’Einstein et ses contraintes 21
Non linéarité du champ gravitationnel : la version mécanique quantique 22
Établissement des équations d’Einstein : Deuxième méthode par application du principe de moindre action d’Hilbert 23
L’action d’Hilbert 24
Le Lagrangien choisi 24
L’équation d’Einstein dans le vide 26
Y a-t-il des conditions sur le Tenseur énergie-impulsion ? 27
Déclinaisons modernes de l’équation d’Einstein par utilisation de variantes de l’action 28
L’introduction d’une constante Cosmologique 28
Des termes de dérivation de la métrique d’ordre supérieur à deux dans l’action 29
Champs scalaires gravitationnels 30
Un tenseur de torsion non nul. 31
Solutions de l’équation d’Einstein 31
Problème des conditions initiales et de leur évolution en Relativité générale 32
Contraintes sur les données initiales 33
Choix d’une jauge 33
Le problème possède toutes les données nécessaires à sa résolution 35
Discussion sur l’existence de solutions 35
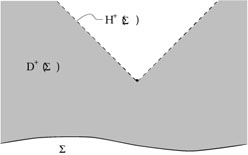
Domaines de dépendance 36
Difficultés qu’on peut rencontrer 36
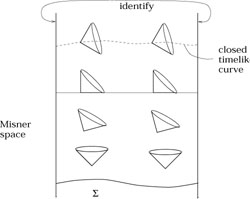
Espace de Misner 37
Singularités 38
Synthèse des difficultés 38
4 – GRAVITATION 5
Introduction 5
Principe d’équivalence d’Einstein
De la définition et de la mesure de l’accélération gravitationnelle
Définition du mouvement chute libre dans un champ gravitationnel
De la difficulté de construire un référentiel étendu à l’espace-temps entier en Relativité générale.10
Faute de mieux, construisons un référentiel local
Premières conséquences
La gravitation est la manifestation de la courbure de l’espace-temps
Décalage spectral comme conséquence directe du PEE
La courbure nécessaire de l’espace-temps
Un peu de formalisme mathématique
La courbure de l’espace-temps est suffisante
Vers les équations du champ.
Exemples pratiques d’application du principe de covariance
L’application du principe de covariance peut conduire à des ambiguïtés
Limites du principe d’équivalence
Exemple de l’introduction d’une constante de couplage entre champs.
À l’échelle macroscopique la constante de couplage peut être négligée.
Etablissement de l’équation d’Einstein
Première méthode d’établissement des équations d’Einstein: par généralisation de l’équation de Poisson
La limite Newtonienne
L’équation d’Einstein
La signification de l’équation d’Einstein et ses contraintes
Non linéarité du champ gravitationnel : la version mécanique quantique
L’action d’Hilbert
Le Lagrangien choisi
L’équation d’Einstein dans le vide
L’équation complète, Contraintes sur le tenseur énergie-impulsion
Déclinaisons modernes de l’équation d’Einstein par utilisation de variantes de l’action
L’introduction d’une constante Cosmologique
Des termes de dérivation de la métrique d’ordre supérieur à deux dans l’action
Champs scalaires gravitationnels
Solutions de l’équation d’Einstein
Problème des conditions initiales et de leur évolution en Relativité générale
Contraintes sur les données initiales
Le problème possède toutes les données nécessaires à sa résolution
Discussion sur l’existence de solutions
Difficultés qu’on peut rencontrer
4
- GRAVITATION
Introduction
La physique de la gravitation dans le cadre de la relativité générale présente deux aspects en interaction profonde.
La courbure de l’espace-temps, manifestation de la gravité, agit sur la matière et l’énergie sous toutes ces formes.
La matière et l’énergie, représentées par le tenseur énergie-impulsion influe sur l’espace-temps et génère une courbure.
Dans un cours magistral classique, il paraîtrait logique de commencer par le premier point en établissant les lois gouvernant la physique dans un espace courbe et en déduisant leurs conséquences.
Nonobstant la logique, nous allons essayer une approche plus motivante, partant des principes de base de la physique, en essayant de montrer qu’ils conduisent naturellement à pratiquement une seule théorie physique.
Principe d’équivalence
L’essentiel de ces principes physiques se résume au principe d’équivalence qui se décline en plusieurs versions.
Principe d’équivalence faible
La plus ancienne de ces versions est due à Galilée et Newton est appelée le principe d’équivalence faible (PEF).
Il stipule l’égalité de la masse inerte et de la masse pesante. La deuxième loi de Newton (1) nous indique la signification de la masse inerte.
L’accélération prise par un objet soumis à une force est proportionnelle à
la force, le coefficient de proportionnalité étant la masse inerte mi :
|
(1) |
La masse inerte a un caractère universel, traduisant la “résistance” au changement d’état d’un objet (modifiant son énergie par rapport au référentiel considéré), quand on exerce une action sur lui, quelle qu’en soit la nature..
La Relativité Restreinte nous éclaire sur la signification de cette résistance puisque la variation d’énergie qui correspond à celle transférée par l’action de la force pendant un temps t dépend de la masse.
dE = d (mc²) = d (m0.c².(1-v²/c²)-1/2) = m0.c².d(1-v²/c²)-1/2
La masse inerte apparaît comme le coefficient d’ajustement de l’accroissement de vitesse compte tenu de l’énergie transférée. Elle correspond à la quantité d’énergie de l’objet
Par ailleurs, la gravitation agissant sur ce même
objet, produit une force proportionnelle au gradient du champ scalaire
, appelé potentiel
gravitationnel. Cette constante de proportionnalité est appelée masse
gravitationnelle ou masse grave mg :
|
(2) |
De ces définitions, on voit que rien ne relie l’une à l’autre. L’une, mi, traduit la quantité d’énergie de l’objet, l’autre son coefficient de couplage avec le champ gravitationnel, sa charge gravitationnelle (cf interaction électromagnétique par exemple).
Par ses expériences à la tour de Pise, Galilée a montré que, curieusement tous les corps, quelle que soit leur nature, leur masse, tombaient de la même manière (accélération constante) dans le champ de gravitation terrestre (abstraction faite de la résistance de l’air).
En mécanique newtonienne ceci s’exprime simplement.
|
(3) |
||
|
|
et |
|
|
(4) |
||
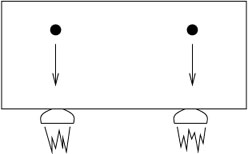
L’universalité de la gravitation conformément au PEF, implique qu’un observateur, enfermé dans un laboratoire sans fenêtres, coupé du monde, et faisant des observations sur la chute des corps, les verra tous tomber avec la même accélération où qu’il soit. La valeur de cette accélération sera différente selon l’endroit où il se trouve (Sur Terre, sur Jupiter, sur la Lune ou loin de tout corps céleste en apesanteur). Mais localement elle sera la même pour tous les corps, éventuellement nulle dans le dernier cas.
Mais le résultat de la chute des corps, serait différent si l’observateur était soumis simultanément à une accélération constante, cela changerait la valeur l’accélération des particules en chute libre dans le champ gravitationnel, dans le laboratoire (Une accélération de même valeur et direction que celle résultant du champ gravitationnel, “annule” l’action de ce dernier, transformant le laboratoire en référentiel inertiel).
Le PEF implique donc qu’il n’y a pas moyen de distinguer “l’accélération a” produite par un champ de gravitation d’une accélération pure de la même valeur "a". (hors d’un champ de gravitation)
Ceci résulte de l’universalité de la gravitation. On peut distinguer ces deux états dans le cas d’une accélération produit par un champ électromagnétique en observant le comportement de charges différentes en intensité en signe et de même masse inertielle, mais cela n’est pas possible avec la gravitation car la charge gravitationnelle est nécessairement proportionnelle à ma masse inerte.
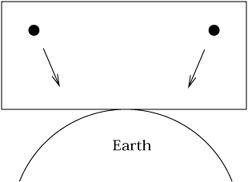
Un bémol cependant, remarquons que cela s’applique à des régions de l’espace
ou le champ gravitationnel est quasi constant, ce qui n’est pas le cas, à
proximité d’une planète par exemple, où à grande échelle on observerait une
convergence des trajectoires vers le centre dans le cas de l’effet
gravitationnel, permettant de le distinguer d’une accélération pure.
|
|
|
|
En conséquence le PEF statuant qu’une force de gravitation est équivalente à un mouvement accéléré, est valide pour des domaines de l’espace, limités ou le champ de gravitation est (quasi) constant.
Autrement des forces de marée liées à l’inhomogénéité du champ peuvent être détectées.
Principe d’équivalence
d’Einstein
Avec la Relativité restreinte, le concept de masse s’est généralisé en celui d’énergie et de quantité de mouvement (E = mc2 etc.). Einstein a trouvé donc naturel de généraliser le PEF dans ce contexte.
L’idée est que le même observateur que précédemment dans le même contexte, n’a aucun moyen de distinguer l’action d’un champ gravitationnel (constant) d’une accélération constante (correspondante) quelles que soient les expériences qu’il fait (pas seulement la chute des corps).
Cette extension porte le nom de principe d’équivalence d’Einstein (PEE).
Dans des régions d’espace suffisamment petites, les lois de la physique se ramènent celles de la Relativité Restreinte, ce qui fait qu’il est impossible de détecter un champ gravitationnel. En fait il est difficile d’imaginer une théorie conforme au PEF qui violerait le PEE.
Si on prend un atome d’hydrogène où le proton et l’électron sont liés par l’interaction électromagnétique. Sa masse est inférieure à la somme des masses du proton et de l’électron non liés du fait de l’énergie de liaison négative (il faut fournir de l’énergie pour arracher l’électron à l’atome).
D'après le PEF la masse grave de l’atome est donc inférieure à la somme des masses de ses constituants, ce qui veut dire que le champ électromagnétique de liaison se couple avec le champ gravitationnel de façon à effacer le défaut de masse. Ceci confirme que la gravitation se couple avec toutes les formes d’énergie et d’impulsion et pas seulement avec la masse au repos ce qui correspond aux revendications du PEE.
On peut bien sur imaginer des contre exemples comme une théorie de la gravitation obéissant aux mêmes règles mais qui ferait en plus tourner les particules lorsqu’elles tombent. Cette théorie obéirait au PEF mais pas au PEE, puisqu’on pourrait détecter la présence d’un champ de gravitation.
De telles théories paraissent hautement spéculatives, mais aucune loi de la nature ne semble s’y opposer.
Quelquefois on distingue les lois y compris les lois gravitationnelles de la physique et les lois non compris les lois gravitationnelles de la physique et le PEE est censé ne s’appliquer qu’à ces dernières.
Principe d’équivalence fort
On définit donc le principe d’équivalence fort (PEF) qui explicitement inclut tout (en particulier le couplage de la gravitation avec elle-même). Dans la suite de ce cours il n’est pas fait de distinguo entre les deux.
Le PEE implique (ou du moins suggère) que la courbure de l’espace résulte de l’action de la gravitation.
De la définition et de la mesure de l’accélération gravitationnelle
Rappelons qu’en RR les référentiels inertiels jouent un rôle essentiel, sans qu’il soit possible de désigner l’un d’entre eux comme référence absolue (au repos). On ne peut définir qu’une famille (en mouvement relatif uniforme les uns par rapport aux autres).
L’accélération d’une particule chargée dans un champ électromagnétique est définie uniquement par rapport à ces référentiels.
Le PEE implique qu’on échappe pas à la gravitation pour peu qu’on ait une masse ou une énergie (qu’on existe en quelque sorte).
Comme la charge gravitationnelle nulle n’existe pas, on n’a pas de référence pour mesurer l’action de la seule gravitation sur un objet.
L’accélération due à la gravitation est donc quelque chose qui ne peut pas être définie avec fiabilité, et n’est par conséquent de peu d’ utilité.
Définition du mouvement chute
libre dans un champ gravitationnel
Par contre, il est plus pertinent de bien définir les propriétés " non accéléré " et " chute libre", ce que nous allons faire.
Ce point de vue est à l’origine de l’idée que la gravité n’est pas une force.
Une force est quelque chose qui produit une accélération.
Dans notre cas, nous avons vu la difficulté d’isoler l’accélération due à la seule gravitation, du fait de l’absence de charge nulle, permettant sa mesure directe.
.
À la place, nous définissons l’accélération zéro comme le fait de se mouvoir librement comme dans un référentiel inertiel, concept connu de la RR, mais ceci, qu’un champ gravitationnel soit présent ou non.
Cette proposition apparemment anodine a de profondes implications sur la nature de l’espace-temps.
De la difficulté de
construire un référentiel étendu à l’espace-temps entier en Relativité générale
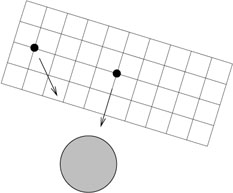
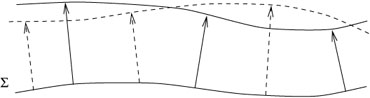
En RR, nous avions un procédé qui partant d’un point permettait de construire un référentiel couvrant tout l’espace-temps, en arpentant le référentiel à l’aide de règles rigides et en y attachant des horloges que l’on sait synchroniser.
Maintenant du fait de l’inhomogénéité du champ gravitationnel, ce n’est plus possible.
Si on commence à partir d’un référentiel local chute libre à construire une structure étendue à base de règles rigides, les objets en chute libre à une certaine distance du point de départ vont être animés d’un mouvement accéléré vis-à-vis du référentiel de départ comme l’indique la figure suivante.
|
|
Faute de mieux, construisons un référentiel local
La solution est de retenir la notion de référentiel inertiel local, mais d’abandonner l’espoir qu’il puisse s’étendre de façon unique dans l’espace-temps.
À la place, définissons des référentiels inertiels locaux dans lesquels le mouvement chute libre des particules est respecté dans des domaines suffisamment petits d’espace-temps (en pratique, pas nécessairement très petits si le champ varie peu, mais, à la limite infiniment petits, si nécessaire pour le calcul) :
Premières conséquences
C’est ce qu’on peut faire de mieux, mais cela n’est pas sans conséquences.
Par exemple, comment parler avec certitude de la vitesse d’objets éloignés, alors que le référentiel inertiel auquel ils sont attachés est indépendant du nôtre ?
Pour l’instant nous n’avons parlé que de physique, sans aller à la conclusion que l’espace-temps doit être décrit par une variété différentiable courbée. Pourtant une telle conclusion est bien appropriée.
L’idée que les lois de la RR sont respectées dans des régions suffisamment petites de l’espace-temps et qu’en conséquence des référentiels locaux inertiels peuvent être construits dans de telles régions correspond à la possibilité de définir un système de coordonnées normales de Riemann en n’importe quel point de la variété, coordonnées dans lesquelles la métrique revêt sa forme canonique et les symboles de Christoffel s’annulent.
L’impossibilité de comparer des vitesses (vecteurs) pour des régions très éloignées correspond à la dépendance du chemin de transport parallèle dans une variété courbée.
La gravitation est la
manifestation de la courbure de l’espace-temps
Ces considérations suffirent à Einstein pour affirmer l’idée que la gravitation était une manifestation de la courbure de l’espace-temps.
En fait on peut être encore plus convaincant (même si on ne peut pas le prouver, les théories scientifiques ne pouvant pas être prouvées, seulement mises en défaut et encore pas vraiment selon Thomas Kuhn).
Ne boudons pas les arguments convaincants plausibles, surtout s’ils conduisent à des théories empiriquement satisfaisantes.
Décalage spectral comme
conséquence directe du PEE
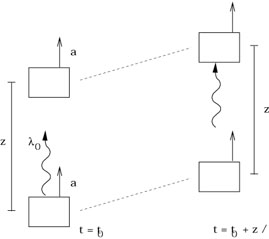
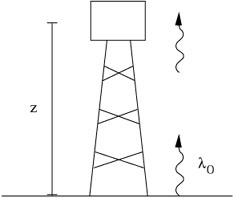
Considérons la prédiction célèbre du PEE du décalage gravitationnel vers le rouge.
Soit deux boites séparées par une distance z, se déplaçant loin de toute matière (en l’absence de champ gravitationnel) avec une accélération constante a.
Au temps t0, la boite de traîne émet un photon de longueur d’ondel0
Les boites restent à distance constante, donc le
photon atteint la boite de tête après un temps
t
= z/c dans le système de référence des boites.
Pendant ce temps les
boites ont acquis une vitesse additionnellev
= at = az/c
En conséquence le photon atteignant la boite de tête subit un décalage vers
le rouge, lié à l’effet Doppler classique, de :
|
(5) |
On supposev/c petit, pour
travailler au premier ordre.
Conformément au PEE, le même phénomène doit se produire dans un champ de gravitation uniforme.
La courbure nécessaire de
l’espace-temps
Imaginons une tour de hauteur z située sur une planète, munie d’un champ de gravitation d’intensité ag(accélération due à la gravitation en mécanique classique)
Cette situation est réputée non distinguable de la précédente, du point de vue d’un observateur dans une boite au sommet de la tour (capable de détecter le photon, mais coupé du monde extérieur)
En conséquence, le photon émis depuis le sol avec une longueur d’onde l0 doit être décalée vers le rouge
de :
|
(6) |
C’est le fameux décalage vers le rouge gravitationnel, conséquence directe du PEE, sans avoir besoin des équations de la Relativité générale. Il a été vérifié expérimentalement d’abord par Pound et Rebka en 1960. Ils ont utilisé l’effet Mössbauer pour mesurer le changement de fréquence de rayons γ dans cette configuration au Jefferson Labs à Harvard.
La formule pour le décalage vers le rouge utilise
souvent le potentiel Newtonien , où ag= 
. (Le signe est l’inverse de la
convention du fait ag est l’accélération du
référentiel, pas de la particule dans ce référentiel!. Un gradient variable
de est l’équivalent d’une accélération
dépendant du temps, et la vitesse moyenne équivalente est donnée par
intégration entre le temps d’émission et de détection du photon. Cela
donne :
|
(7) |
Où est la variation du potentiel
gravitationnel où on a posé c =1.
Cette formule simple pour le décalage vers le rouge gravitationnel reste valable dans un cas plus général.
Bien sur en utilisant le potentiel gravitationnel, on se réduit aux cas des champs faibles, mais c’est suffisant dans bien des cas, pour en observer les effets.
L’effet gravitationnel de décalage vers le rouge amène un autre argument en faveur de la courbure de l’espace.
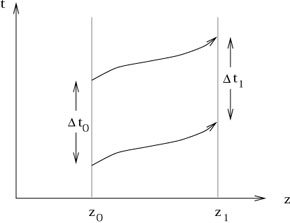
Représentons un diagramme spatio- temporel de l’expérience précédente.
|
|
Le physicien au sol émet un rayon lumineux de longueur d’onde l0 d’une altitude z0, qui voyage vers le sommet de la tour d’altitude z1.
Le temps entre deux
crêtes de l’onde émise est t0 =l0 /c, et le
même intervalle pour la détection estt1 = l1 /c. Comme
le champ est statique les chemins spatio-temporels du début et de la fin
de l’intervalle sont strictement parallèles (ne dépend pas du temps d’émission)
On l’a représenté par une courbe quelconque ne représentant pas nécessairement le chemin réel, car là n’est pas le propos.
(La géométrie
élémentaire voudrait que les tempst0 et
t1
soient les mêmes.
Ce n’est pas le cas,
du fait du décalage gravitationnel vers le rouge qui implique que
t1
> t0, que l’on peut
interpréter comme le fait que l’horloge au sommet bat plus vite
Où est l’erreur ?
Notre géométrie simple (Euclidienne) ne s’applique pas et on doit appliquer une géométrie correspondant à un espace courbé (l’échelle de temps n’est pas uniforme sur le diagramme, elle dépend de z).
Tout ceci nous incite à penser qu’en présence de la gravitation, l’espace-temps doit être pensé en termes de variété courbe.
Supposons ceci exact et regardons comment la physique s’applique dans un tel espace-temps.
Le PEE nous indique que dans des régions suffisamment petites les lois de la RR s’appliquent.
Un peu de formalisme
mathématique
Dans le langage mathématique spécifique aux variétés ceci doit être interprété comme suit:
Les lois, lorsqu’elles sont formulées dans des coordonnées normales Riemanniennes (CNR) xm à un point p, sont décrites par les équations qui ont la même forme que dans un espace plat (Euclidien).
L’exemple le plus simple est celui des particules en chute libre (non accélérées).
Dans un espace Euclidien elles suivent une
trajectoire rectiligne ce qui est exprimé par les équations par l’annulation de
la dérivée seconde du chemin paramétré xm (
) :
|
(8) |
Selon le PEE cette équation doit être valide dans un espace courbé a condition qu’elle soit exprimée en coordonnées CNR.
Mais qu’advient-il de cette équation dans les autres systèmes de coordonnées.
Telle quelle, (8) n’est pas une équation entre tenseurs.
Il n’y a qu’une équation tensorielle qui se ramène à (8) quand le symbole de
Christoffel s’annule c’est :
|
(9) |
Bien sûr c’est l’équation géodésique. En Relativité Générale, les particules en chute libre suivent les géodésiques de l’espace-temps courbé comme nous l’avons déjà mentionné, mais nous voyons maintenant pourquoi.
Du fait du mouvement chute libre nous avons déduit que la courbure de l’espace-temps était nécessaire pour décrire la gravitation, nous n’avons pas montré que c’était suffisant.
La courbure de l’espace-temps est suffisante
Pour ce faire, montrons comment les résultats de la gravitation de Newton s’inscrivent dans ce schéma.
Limite Newtonienne
Définissons la limite Newtonienne par trois conditions :
La vitesse des particules est faible devant celle de la lumière,
le Champ gravitationnel est faible (considéré comme une perturbation de l’espace de Minkowski),
le champ est statique (ne dépend pas du temps)
Voyons l’effet de ces conditions lorsque appliqué à l’équation géodésique en prenant le temps propre τ comme paramètre affine.
“Vitesse faible” signifie :
|
(10) |
L’équation géodésique devient :
|
(11) |
Comme le champ est statique, les symboles de Christoffel concernés Gm00 se simplifient :
|
(12) |
Enfin la faiblesse du champ gravitationnel nous autorise a écrire la métrique
sous la forme Minkowskienne entachée d’une petite perturbation :
|
(13) |
On travaille en coordonnées cartésiennes donc hmn est la forme canonique de la métrique. La faiblesse de la perturbation n’a pas de sens dans d’autres coordonnées.
Par définition la métrique inverse est gmn telle que
gmngns =dsm. Au premier ordre en
h, cela donne
|
(14) |
En fait on peut utiliser la métrique de Minkowski pour élever ou abaisser les indices de n’importe quel objet de n’importe quel ordre en h, car les corrections ne vont affecter que les ordres supérieurs.
En synthèse il vient :
|
(15) |
L’équation géodésique (11) devient :
|
(16) |
Comme ¶0h00 =
0, la composante m= 0 est alors :
|
(17) |
Ceci indique que dt/dt est constant. Considérons les composantes d’espace de (16), On rappelle que les composantes d’espace de hmn sont juste celles de la matrice identité 3 × 3.
Il vient :
|
(18) |
Divisons les deux membres par (dt/dt)². Ceci a pour effet de changer
la dérivation du membre de gauche de
par t,
il nous reste :
|
(19) |
Cela commence à ressembler à la théorie de la gravitation de Newton (4.4),
surtout si on pose :
|
(20) |
Soit encore :
|
(21) |
Nous avons donc montré que la courbure de l’espace est suffisante pour décrire la gravitation dans le cas de la limite Newtonienne, tant que la métrique est de la forme (21).
On remarque qu’au potentiel gravitationnel F (notion de mécanique classique) correspond, dans l’approximation newtonienne, une “courbure” - h00 /2 de la géométrie de l’espace-temps (notion de Relativité générale).
Vers les équations du champ
Il reste à établir les équations du champ pour cette métrique. Ces
équations, dans les mêmes conditions de l’approximation Newtonienne devront
produire,
|
(22) |
dans le cas d’un champ gravitationnel généré par une masse unique ponctuelle. Nous verrons cela bientôt.
“Principe de
covariance”: Comment les lois se conservent quand on passe d’un référentiel à
un autre
Notre prochaine tâche est de montrer comment les autres lois de la physique, autres que celles gouvernant la chute libre des corps sont affectées par la courbure de l’espace-temps.
Le paradigme suivant est utilisé. Puisque les particules en chute libre (non soumises à d’autres interactions que le champ gravitationnel) suivent les géodésiques de l’espace-temps, prenez les lois de la physique dans un espace Euclidien écrites classiquement en termes de dérivées partielles et comme conformément au principe d’équivalence, cette loi doit toujours être valable si exposée en coordonnées Normales Riemanniennes (CNR), traduisez la loi en termes de relations entre tenseurs en changeant par exemple les dérivées partielles en dérivées covariantes.
En CNR, la version de la loi va se ramener à celle d’origine relative à l’espace-temps plat (RR).
Mais comme les tenseurs sont des objets indépendants des coordonnées, cette version sera valide dans n’importe quel système de coordonnées.
Cette procédure est quelquefois appelée le principe de covariance, ce qui est un peu excessif, car c’est en fait une pure conséquence du PEE, avec la condition mathématique complémentaire que ces lois doivent être indépendantes du système de coordonnées. Un autre nom pour cette règle est le point virgule remplace la virgule, du fait des conventions utilisées pour les dérivées partielles "," et les dérivées covariantes";"
L’exigence d’avoir des lois indépendantes du système de coordonnées est impératif.
Pour toute théorie raisonnable, son non respect est inconcevable.
Si on réalise une expérience, les résultats de cette même expérience vus par deux observateurs utilisant des systèmes de coordonnées différents, pour la décrire, doivent être les mêmes.
Nous avons implicitement utilisé le principe de covariance (quel que soit son appellation) quand nous avons dit que les particules libres suivaient les géodésiques. La plupart du temps, c’est très simple de l’appliquer aux cas intéressants.
Exemples pratiques d’application du principe de covariance
Considérons par exemple la formule de conservation de l’énergie dans
l’espace plat ¶mTmn
= 0. L’adaptation à un espace courbe est immédiate :
|
(23) |
Cette équation exprime la conservation de l’énergie en présence d’un champ gravitationnel. Malheureusement ce n’est pas toujours aussi immédiat.
Prenons les équations de Maxwell de la RR, où il semble que l’on puisse appliquer le principe de covariance directement, appliquons-le :
L’équation non homogène ¶mFmn
= 4
Jn, devient :
|
(24) |
Tandis que l’équation homogène ¶[mFnl
] = 0
devient :
|
(25) |
D'autre part, on peut aussi écrire les équations de Maxwell en espace plat
en termes de formes différentielles comme suit :
|
(26) |
et
|
(27) |
Celles-ci sont déjà sous forme tensorielle, puisque nous avons montré que la dérivée externe est un opérateur de tenseur parfaitement défini, quel que soit la connexion métrique.
L’application du
principe de covariance peut conduire à des ambiguïtés
On peut légitimement se demander si l’écriture des lois de la physique sous forme tensorielle ne permet d’obtenir qu’une seule réponse. De fait nous avons déjà mentionné précédemment que ce sont les versions des formes différentielles des équations de Maxwell qui doivent être considérées comme fondamentales. Dans cas, il se trouve qu’il n’y a aucune différence du fait qu’en l’absence de torsion (26) est identique à (24) et (27) à (25), le terme symétrique de la connexion métrique n’intervient pas.
Itou en ce qui concerne la définition du tenseur d’intensité de champ en
termes de potentiel Am, il peut être écrit :
|
(28) |
et tout aussi bien :
|
(29) |
Le souci d’unicité est donc réel., Imaginons que deux champs de
vecteurs Xm et Yn suivent une loi dans un espace
plat donnée par :
|
(30) |
Cela pose un problème d’écriture sous forme tensorielle. Les dérivées
partielles sont commutatives alors que les dérivées covariantes ne le sont pas.
Une substitution bestiale dans (30) conduit à deux réponses différentes selon
l’ordre des dérivées partielles, ordre auquel n’est pas sensible l’équation
dans l’espace plat. La différence est :
|
(31) |
Les règles de transposition des lois d’un espace plat à un espace courbé ne nous renseignent pas sur l’ordre des dérivées à prendre en compte et ne nous indique donc pas si un terme tel que (31) va apparaître en présence de gravitation.
Cette ambiguïté liée à l’ordre des dérivées covariantes est similaire à celle liée à l’ordre des opérateurs (non commutatifs) en mécanique quantique.
On trouve dans la littérature diverses règles pour traiter ces ambiguïtés, la plupart tournant autour de recommandations pertinentes concernant la conservation de l’invariance de jauge de l’électromagnétisme.
Mais si on creuse un peu, on s’aperçoit qu’il n’y a pas de règle théorique pour résoudre ce problème. En fait, il peut y avoir plusieurs manières d’adapter les lois de la physique à un espace courbe et in fine c’est l’expérience qui permettra de trancher entre les alternatives.
Limites du principe
d’équivalence
Pour être complètement honnête, il faut reconnaître que le principe d’équivalence malgré sa puissance heuristique indiscutable ne mérite pas d’être érigé en principe fondamental de la nature.
Les travaux les plus récents mettent en doute l’exactitude absolue du PEE.
Exemple de l’introduction d’une constante de couplage entre
champs
Considérons la variante suivante de (24) :
|
(32) |
Où R est le scalaire de Ricci et α une constante de couplage. Si cette équation décrit correctement l’électromagnétisme dans un espace-temps courbé, on pourra mesurer R dans une zone même arbitrairement petite en faisant des expériences avec des particules chargées.
Le principe d’équivalence impose donc α = 0.
Pourtant (32) a tous les attributs d’une équation plausible, qui respecte la conservation de la charge, toutes les autres contraintes de l’électromagnétisme, qui se ramène à l’équation bien connue dans un espace plat (R=0).
Au royaume de la mécanique quantique, tous les couplages des différents champs (tels que la gravitation et l’électromagnétisme) cohérents avec les symétries de la théorie (dans ce cas l’invariance de jauge) sont permis.
Pourquoi alors est on amené à poser α = 0 ? Pour une raison d’échelle.
Remarquons que le tenseur de Rici contient les dérivées secondes de la métrique, grandeur sans dimension donc R a les dimensions d’une (longueur) -2 (avec c = 1). Donc α doit avoir les dimensions d’une (longueur)2.
À l’échelle
macroscopique la constante de couplage peut être négligée
Mais comme le couplage représenté par
est d’origine gravitationnelle la
seule possibilité plausible pour l’échelle de longueur est :
|
(33) |
où lP est la longueur de Planck :
|
(34) |
où 
est évidemment la constante de Planck.
On voit que l’échelle de longueur correspondant à ce couplage est très petite,
et dans n’importe quelle expérience réalisable l’échelle de variation du champ
gravitationnel va être considérablement plus grande.
On peut donc ignorer sans sourciller le terme qui
viole le PEE, du fait queR est
probablement un nombre extraordinairement petit complètement hors de portée de
toute expérimentation.
Mais gardons présent ce fait à l’esprit, la théorie ne devant pas toujours être limitée par les possibilités d’observations
Établissement de
l’équation d’Einstein
Maintenant que nous avons établi comment les lois de la physique de l’espace Euclidien peuvent être transposées dans un espace Courbé, nous sommes en mesure de finir d’établir la théorie de la Relativité en introduisant les équations du champ d’Einstein qui régissent l’action de l’énergie et de la quantité de mouvement sur la métrique.
Nous allons utiliser deux méthodes différentes pour cela.
Première méthode d’établissement des équations
d’Einstein : par généralisation de l’équation de Poisson
La première repose sur l’approche originale d’Einstein, plus intuitive que formelle et la seconde plus formelle sur la minimisation de l’action.
Einstein cherchait à généraliser l’équation de Poisson valable en mécanique
Newtonienne, rappelée ci-dessous :
|
(35) |
Où Ѳ= dij¶i¶j est le Laplacien
(espace) et
r est la densité de masse. (La forme
explicite de donnée en (22) est une
solution de (35), dans le cas de distribution de masse " ponctuelle")
Quelles autres caractéristiques, l’équation que nous recherchons doit-elle posséder ?
Dans le terme de gauche de (35) nous avons un opérateur différentiel au deuxième ordre du potentiel gravitationnel et le terme de droite décrit la répartition de masse.
La généralisation Relativiste doit s’exprimer en termes de relations entre tenseurs.
Nous savons que la généralisation tensorielle d’une densité de masse est le tenseur énergie-impulsion Tmn, alors que le potentiel gravitationnel doit être remplacé par un tenseur dépendant de la métrique.
Il est alors naturel de poser Tmn proportionnel à un tenseur contenant des dérivées d’ordre deux de la métrique.
En utilisant (21) pour la métrique pour la limite Newtonienne et T00
=
r, on voit que, dans les
conditions de cette limite, l’équation doit donner :
|
(36) |
Mais bien sûr, cette équation doit être tensorielle.
Le membre de gauche de (36) ne se généralise pas de façon évidente à un tenseur.
Une première tentative consiste à appliquer le
d’alembertien 
= ÑmÑm
sur la métrique gmn,
mais cela donne identiquement zéro, par principe, compte tenu de la nature du
tenseur métrique.
Par chance, nous connaissons le tenseur de Riemann Rrsmn. construit à partir des dérivées premières et secondes de la Métrique et qui, lui, n’est pas identiquement nul. Il n’a pas le bon nombre d’indices mais on peut le contracter pour former le tenseur de Ricci Rmn qui convient et est de plus symétrique.
Àce point on peut raisonnablement penser que les équations du champ
sont :
|
|
(37) |
Avec une constante d’ajustement
.
En fait Einstein proposa cette équation. Un problème de taille pourtant
concernant la conservation de l’énergie. Conformément au principe d’équivalence
la conservation de l’énergie Impulsion dans un espace courbe s’écrit :
|
|
(38) |
Ce qui implique :
|
|
(39) |
Ce qui n’est certainement pas vrai dans une géométrie arbitraire. Rappelons
que l’identité de Bianchi implique :
|
|
(40) |
Si (39) est exact alors (40) implique ÑnR = 0 (40 bis)
Comme l’équation (37) que nous proposons implique (en la multipliant par gmn) que :
R =
gmnTmn = T, en prenant aussi en
compte les contraintes (39) et (40 bis), nous avons :
|
|
(41) |
La dérivée covariante d’un scalaire est égale à sa dérivée partielle, donc (41) nous dit que T est constant dans l’espace-temps, ce qui est hautement non plausible, car T = 0 dans le vide et T > 0 en présence de matière. Il faut trouver autre chose.
(En fait, on triche un peu en prenant l’équation ÑmT mn = 0, à la lettre. Si, comme on l’a dit, le principe d’équivalence n’est vrai qu’en première approximation, on peut imaginer qu’il y a des termes non nuls dans le membre de droite concernant le tenseur de courbure. Nous préciserons ce point ultérieurement pour montrer qu’ils doivent être strictement nuls.)
En fait la solution saute aux yeux puisqu’on connaît un tenseur (0,2)
symétrique construit à partir du tenseur de Ricci qui est conservé par
construction: le tenseur d’Einstein :
|
|
(42) |
Qui satisfait toujours ÑmGmn = 0. Nous sommes conduits à
proposer :
|
|
(43) |
comme équation du champ pour la métrique..
Cette équation remplit toutes les conditions requises: Le terme de droite est l’expression covariante de la densité d’énergie-impulsion sous forme d’un tenseur (0,2) symétrique et satisfaisant au principe de conservation, tandis que le membre de gauche est aussi un tenseur (0,2) symétrique et satisfaisant au même principe de conservation construit sur les dérivées premières et secondes de la métrique.
Regardons comment cela rend compte de la gravitation telle que nous la connaissons.
Pour ce faire contractons les deux membres. (43) donne (en quatre
dimensions) :
|
|
(44) |
Utilisons ce résultat et reportons dans (43) alors :
|
|
(45) |
C’est la même équation, juste écrite différemment
La limite Newtonienne
On aimerait vérifier que cela prédit bien la loi de la gravitation de Newton dans les hypothèses idoines.
Dans ces conditions l’énergie de la matière au
repos r = T00 est
très supérieure aux autres termes de Tmn on va se focaliser sur le composant m = 0, 
= 0 de (45). Dans la limite du champ
faible on écrit conformément à (13) et (14)) :
|
|
(46) |
La trace du tenseur énergie-impulsion au premier ordre est :
|
|
(47) |
Reportons la dans (45),on obtient :
|
|
(48) |
Cette équation relie les dérivées de la métrique à la densité d’énergie.
Pour trouver l’expression explicite en termes de métrique nous devons évaluer R00
= Rl0l 0. En fait nous n’avons besoin
que de Ri0i0, car R0000
= 0. Ce qui donne :
|
|
(49) |
Le second terme est une dérivée par rapport au temps qui est nulle pour le
champ statique. Le troisième et quatrième sont d’ordre supérieur et peuvent
être négligés. Il nous reste Ri0j0= ¶jGi00. De ceci on tire :
|
(50) |
En comparant à (48), on voit que la composante 00 de (43) en limite
newtonienne prédit :
|
|
(51) |
Et c’est
exactement (36), si on pose = 8G.
Notre intuition nous a guidée utilement. Avec cette normalisation liée aux conditions aux limites Newtoniennes, nous avons maintenant complètement déterminé l’équation d’Einstein
L’équation
d’Einstein
|
|
(52) |
Elle nous dit comment la courbure de l’espace-temps réagit en présence d’énergie-impulsion.
Einstein trouvait le membre de gauche géométrique de l’équation sympathique tandis que celui de droite paraissait quelque chose de moins contraignant.
La signification de
l’équation d’Einstein et ses contraintes
On peut voir les équations d’Einstein comme des équations différentielles du second ordre sur le tenseur de champ métrique gmn. Il y a en principe dix équations indépendantes (tous les tenseurs à deux indices de l’équation sont symétriques), ce qui parait bien correspondre aux 10 fonctions inconnues de la métrique à déterminer (sur les vingt du tenseur de Riemann).
Mais comme l’identité de Bianchi ÑmGmn= 0 représente quatre contraintes sur les fonctions Rmn, il n’y a en réalité que six équations indépendantes dans (52). Ce n’est pas fortuit, car si une métrique est solution de l’équation d’Einstein dans un système de coordonnées xm, elle le sera dans tous
Cela signifie qu’il y a 4 degrés de liberté non physiques dans gmn représentés par les 4 fonctions xm'(xm), et nous que devons escompter que l’équation d’Einstein ne va contraindre que 6 degrés de liberté.
Ces équations différentielles sont en général cauchemardesques à résoudre, les scalaires et tenseurs de Ricci sont des contractions du tenseur de Riemann, qui incluent les dérivées et les produits des symboles de Christoffel, qui eux-mêmes sont construits sur le tenseur métrique inverse et sur les dérivées du tenseur métrique. Pour corser le tout, le tenseur énergie-impulsion Tmn va généralement invoquer également la métrique.
En prime, les équations sont non linéaires, ce qui fait que si on connaît deux solutions, pas question d’espérer en trouver une troisième à partir d’elles.
Il est donc très difficile de résoudre les équations d’Einstein dans le cas général et on doit souvent s’appuyer sur des hypothèses simplificatrices.
Même dans le vide ou le tenseur énergie-impulsion est nul, l’équation
correspondante tirée de (45),
|
|
(53) |
, peut être très difficile à résoudre. Les simplifications les plus courantes invoquent un degré de symétrie significatif, et nous verrons comment cela peut permettre de trouver une solution analytique exacte.
Non linéarité du champ
gravitationnel : la version mécanique quantique
La non linéarité des équations de la Relativité générale est remarquable. Si, en mécanique Newtonienne, le potentiel dû à deux masses ponctuelles est simplement la somme des potentiels de chacune, ceci n’est pas vrai en relativité générale (hors approximation Newtonienne).
La raison physique est que en Relativité Générale le champ gravitationnel se couple avec lui-même.
Cela peut être vu comme une conséquence du principe d’équivalence, si ce n’était pas le cas, un “atome” gravitationnel (deux particules liées par leur attraction mutuelle) aurait une masse inerte (inférieure à la somme des deux masses du fait de l’énergie de liaison négative) différente de la masse pesante.
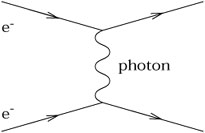
Du point de vue de la physique des particules on peut représenter cela par un diagramme de Feynman.
Rappelons que selon cette représentation, l’interaction électromagnétique de deux électrons peut être vue comme un couplage par échange de photons virtuels.
|
|
Mais comme il n’existe pas de diagramme correspondant à l’échange de photons virtuels entre deux photons, l’électromagnétisme est linéaire.
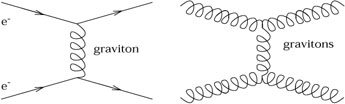
L’interaction gravitationnelle peut être représentée par l’échange de gravitons virtuels (le graviton est le quantum de perturbation de la métrique).
La non linéarité se manifeste par le fait que et les électrons et les gravitons eux-mêmes et tout autre particule se couplent par échange de gravitons virtuels vecteurs de l’interaction gravitationnelle
|
|
Cette particularité n’a rien de caractéristique, elle est partagée par la plupart des théories de jauge, comme la chromodynamique, théorie de l’interaction forte. L’électromagnétisme serait plutôt l’exception, sa linéarité étant caractéristique de la commutativité du groupe (abélien) de jauge U(1) associé
Mais cela est en totale rupture avec la théorie de Newton!.
Pour être honnête, le langage de la mécanique quantique des diagrammes de Feynman n’est pas vraiment approprié à la description de la Relativité générale du fait qu’à ce jour les tentatives de quantification n’ont pas abouti.
Mais ces diagrammes sont un raccourci utile pour se remémorer les interactions qui existent dans la théorie.
Établissement des
équations d’Einstein : Deuxième méthode par application du principe de moindre
action d’Hilbert
Pour conforter notre confiance en les équations d’Einstein que nous avons établies, comme lui, intuitivement, et s’assurer qu’elles sont les bonnes équations du champ pour la métrique, montrons comment on procède aujourd’hui dans le contexte de la physique moderne. On les dérive simplement du principe de moindre action (d’Hilbert).
Historiquement, il y a eu une dispute “en paternité des équations”, Hilbert revendiquant d’être le premier à avoir établi “les équations d’Einstein” en utilisant ce principe de moindre action. Ce point, qui a été contesté par les historiens, semble effectivement inexact. Mais de toute façon, comme ses travaux s’appuyaient sur ceux qu’Einstein avait publiés précédemment et que de son côté Einstein avait aussi indépendamment dérivé ces équations par une autre méthode, c’est à juste titre qu’elles ont été attribuées à Einstein, ce que Hilbert a fini également par reconnaître.
L’action d’Hilbert
Cette action, fort justement appelée action d’Hilbert est l’intégrale sur
l’espace-temps de la densité de Lagrange ("Lagrangien en abrégé, ce
qui est un abus de langage, puisque que pour être précis le Lagrangien
est l’intégrale sur l’espace-temps de la densité de Lagrange).
|
|
(54) |
La densité de Lagrange est une densité de tenseur, type d’objet mathématique qui s’obtient en multipliant (-g)1/2 (g est le déterminant du tenseur) par un scalaire. Quel scalaire dérivant de la métrique doit-on prendre ? Comme nous savons que les dérivées premières de la métrique peuvent être annulées en la mettant sous sa forme canonique, le scalaire en question, pour être utile, doit invoquer au moins les dérivées secondes de cette métrique. Rappelons que le tenseur de Riemann décrit complètement la courbure de l’espace-temps (hors torsion, que nous ne considérons pas dans cette équation). Il est construit sur les dérivées premières et secondes de cette métrique. Le scalaire de Ricci R est le seul scalaire indépendant dérivant de ce tenseur. Il résulte d’une double contraction de ce tenseur. Il paraît tout indiqué.
Ce que nous n’avons pas démontré, mais qui est cependant vrai est que tout tenseur “non dégénéré”, c’est-à-dire qui ne peut pas se ramener à une forme identiquement nulle, construit sur la métrique et ses dérivées premières et secondes peut être exprimé en termes de métrique et du tenseur de Riemann et en est donc linéairement dépendant. Le scalaire de Ricci est bien le seul scalaire indépendant que nous cherchons. Hilbert a donc pensé que ce serait le choix le plus simple pour le Lagrangien.
Le Lagrangien choisi
|
|
(55) |
Les équations du mouvement vont résulter de la variation de l’action dans le
cadre de la métrique. Considérons en fait ces variations dans le cadre de la
métrique inverse gmn,
qui sont plus simples et qui conduisent aux mêmes équations. Comme R = gmnRmn en général on a :
|
|
(56) |
Le second terme
(δS)2 est
dans la forme d’une expression multipliée par
gmn;
regardons de plus près les autres.
Rappelons que le tenseur de Ricci est la contraction du tenseur de Riemann
qui vaut :
|
|
(57) |
La variation de ceci par rapport à la métrique, peut être trouvée en commençant par la variation de la connexion par rapport à la métrique et en la reportant dans cette expression.
Considérons une variation arbitraire de la métrique. En remplaçant :
|
|
(58) |
La variation
Grnm est la
différence entre deux connexions, et est donc un tenseur. Prenons sa dérivée
covariante :
|
|
(59) |
Partant de cette expression (avec un peu de travail) on peut montrer
aisément :
|
|
(60) |
Ce que vous pouvez vérifier.
La contribution du premier terme àS dans (56)
peut alors s’écrire :
|
|
(61) |
Ou nous avons utilisé la compatibilité de la métrique et renommé certains indices neutres.
Maintenant nous avons l’intégrale respectant l’élément de volume naturel associé à la divergence covariante d’un vecteur, qui d’après le théorème de Stockes se ramène à la contribution limite à l’infini qui peut être annulée en annulant la variation à l’infini.(En fait, nous n’avons pas montré que le théorème de Stockes mentionné précédemment en termes de formes différentielles peut être interprété de cette manière, mais vous pouvez vous convaincre facilement que c’est vrai).
Donc ce terme ne contribue en rien à la variation totale
Pour interpréter le terme (δS)3
nous devons utiliser le fait suivant, vrai pour n’importe quelle matrice M :
|
|
(62) |
Ici, ln M est défini par e(ln M) = M. (Pour
les nombres c’est évident, pour les matrices ça l’est un peu moins.) La
variation de cette identité donne :
|
|
(63) |
Ici nous avons utilisé la propriété cyclique de
la trace pour ignorer le fait que M-1 et
M peuvent ne
pas commuter.
Maintenant nous voudrions appliquer cela à la métrique inverse, M = gmn.
Alors det M = g-1 (où g = det gmn),
et :
|
|
(64) |
Substituons dans :
|
|
(65) |
Retournons à (56), et rappelons-nous que (S)1 ne contribue
pas, on trouve :
|
|
(66) |
Comme ceci doit s’annuler pour n’importe quelle variation arbitraire, on est conduit à poser
L’équation
d’Einstein dans le vide
|
|
(67) |
Ce qui correspond à l’équation d’Einstein dans le vide
Le fait que l’application du principe de moindre action conduise à la même équation de champ dans le vide que celle qu’Einstein avait trouvé de façon plus informelle, nous conforte dans notre démarche.
Nous aimerions aller jusqu’au bout et trouver également les équations générales du champ.
Cela signifie que nous devons considérer une action de la forme :
|
|
(68) |
où SM est l’action de la matière, et où nous avons
précédemment normalisé l’action de la gravitation (bien que à proprement
parler, cette normalisation est quelque chose qui dépend des conventions). Si
on suit la même démarche que ci-dessus on arrive à :
|
|
(69) |
Ce qui permet de retrouver l’équation d’Einstein si on pose :
|
|
(70) |
Qu’est ce qui nous permet de procéder à une telle identification? En fait (70) se révèle être le meilleur moyen de définir un tenseur énérgie impulsion symétrique. La partie délicate consiste à montrer qu’il est conservé, ce qui est en fait automatiquement vrai, mais que nous ne justifierons qu’au prochain chapitre.
Si nous disons que (70) produit la meilleure définition du tenseur énergie-impulsion, c’est parce que ce n’est pas la seule qu’on puisse trouver.
Dans l’espace plat de Minkowski, il y a une autre
définition qu’on trouve parfois dans les livres d’électromagnétisme ou de
théorie des champs. Dans ce contexte la conservation de l’énergie-impulsion est
la conséquence de la symétrie du Lagrangien par rapport aux translations de
l’espace-temps. Le théorème de Noether stipule que toute symétrie d’un Lagrangien
engendre une loi de conservation, à l’invariance par rapport aux quatre
translations d’espace-temps correspond un tenseur Smn
tel que ¶mSmn
= 0 (quatre relations, une pour chaque valeur de ). Pour les détails voir Wald ou de
nombreux ouvrages sur la théorie des champs
En appliquant la procédure de Noether pour un Lagrangien qui dépend de
champs Yi et de leurs dérivées
premières ¶mYi, on
obtient :
|
|
(71) |
Où on doit sommer sur i. Vous pouvez vérifier que ce tenseur est conservé en vertu des équations du mouvement d’un champ de matière.
Smn est souvent appelé le “tenseur énergie-impulsion canonique”, mais nous avons de bonnes raisons d’utiliser (70). D'abord et principalement, (70) est en fait ce qui apparaît au membre de droite de l’équation quand nous la dérivons d’une action. Alors qu’il n’est pas toujours possible de généraliser (71) dans un espace courbé.
Et même dans un espace plat, (70) a des avantages; il est manifestement symétrique et garantit l’invariance de jauge, alors que (71) faillit sur ces deux points. Nous nous en tiendrons donc à (70) comme définition du tenseur énergie-impulsion
Y a-t-il des conditions sur le Tenseur
énergie-impulsion ?
Il est quelquefois utile de considérer l’équation d’Einstein sans se référer à la théorie de la matière dont dépend Tmn. Cela nous laisse une bonne dose d’arbitraire. Considérons par exemple la question :
À quelle métrique obéissent les équations d’Einstein ? En l’absence de contraintes sur Tmn, la réponse est " n’importe laquelle ". Simplement choisissez votre métrique, calculez le tenseur d’Einstein Gmn pour cette métrique et posez Tmn égal à Gmn. (Il va être automatiquement conservé du fait de l’identité de Bianchi.) Notre seul souci est l’existence de solutions à l’équation d’Einstein en présence de sources d’énergie et d’impulsion réalistes, quelles qu’elles soient.
La propriété la plus commune demandée à Tmn est qu’il représente des densités d’énergie positive, les masses négatives ne sont pas admises.
Dans un référentiel local inertiel cette condition s’exprime par r = T00 ³ 0. Pour le convertir en expression indépendante des coordonnées nous demandons :
TμνVμVν ≥ 0 pour tous les vecteurs de type temps. (72)
Ceci porte le nom de condition d’énergie faible (Weak Energy Condition soit WEC).
Cette condition parait raisonnable et beaucoup de théorèmes importants au sujet des solutions de la Relativité générale (tel que les théorèmes de singularité de Hawking et Penrose), s’appuient sur cette condition ou quelque chose d’approchant.
Malheureusement, ceci n’est pas gravé dans le marbre, et en fait il est simple d’inventer une autre théorie classique des champs respectable qui viole le WEC de même qu’il est presque impossible d’inventer une théorie quantique des champs qui y soit conforme.
Malgré cela, il est légitime de penser que le WEC tient bon mais dans toutes les conditions sauf les plus extrêmes. (Il y a aussi des conditions d’énergie plus fortes, mais elles plutôt sont moins vraies que le WEC, donc nous ne les considérerons pas….)
Nous avons donc justifié les équations d’Einstein par deux moyens différents:
Comme généralisation de l’équation de Poisson du potentiel gravitationnel Newtonien et comme résultat de variation de l’action la plus simple que nous avons pu inventer pour la métrique.
Déclinaisons modernes de
l’équation d’Einstein par utilisation de variantes de l’action
Le reste du cours va consister à explorer les conséquences de ces équations, mais avant de s’engager dans cette voie regardons de quelle manière ces équations peuvent être modifiées.
Il y a d’innombrables manières de faire, mais nous allons en considérer quatre :
L’introduction d’une constante Cosmologique
Des termes d’ordre supérieur à deux dans l’action
Champs scalaires gravitationnels
Un tenseur de torsion non nul.
L’introduction
d’une constante Cosmologique
La première possibilité est l’introduction d’une constante cosmologique. George Gamow a relevé qu’Einstein l’avait qualifié de plus grande erreur de sa vie. Rappelons que dans notre quête de scalaire pour représenter l’action la plus simple pour la gravitation, nous avons noté que tout scalaire non dégénéré devait contenir au moins des dérivées secondes de la métrique, tout ordre inférieur ne pouvant conduire qu’à des constantes. Bien qu’une constante seule ne soit d’aucun intérêt, son adjonction à l’action conventionnelle de Hilbert a des effets très conséquents.
Considérons donc une action de la forme :
|
|
(73) |
où Λ est une constante. Les
équations du champ résultantes sont :
|
|
(74) |
Et bien sûr, il y aurait eu un tenseur énergie-impulsion dans le membre de droite si nous avions inclus l’action pour la matière.
Λ est la constante cosmologique. Elle a été originellement introduite par Einstein quand il lui apparut clairement que ses équations n’avaient pas de solution correspondant à une cosmologie statique (Univers matériel immuable) s’il n’était pas vide de matière. En ajustant la constante cosmologique, il est possible de trouver une solution statique, mais elle est instable vis-à-vis de petites perturbations. De plus quand Hubble, montra que l’Univers était en expansion, la recherche de solutions statiques devint moins cruciale et Einstein répudia cette hypothèse. Peine perdue, car la suite montra que la constante cosmologique avait la peau dure.
On peut si on le désire faire passer le terme additionnel de (74) à droite de l’équation et le considérer comme une sorte de tenseur énergie-impulsion avec Tmn = - Λgmn (il est évidemment conservé du fait que la métrique l’est).
Donc Λ peut être interprété comme la “densité d’énergie du vide”, une source d’énergie-impulsion présente même en l’absence de champs matériels. Cette interprétation est importante car la théorie quantique des champs prédit que le vide doit avoir une sorte d’énergie-impulsion
En
mécanique quantique classique, un oscillateur harmonique de fréquence
et d’énergie minimum classique E0
= 0, lorsqu’il est quantifié, a un état de base qui correspond à une énergie E0
= (1/2).. Un champ quantifié peut être
représenté par une série comprenant une infinité d’oscillateurs harmoniques
dont chaque mode contribue à l’énergie de l’état de base. Le résultat est bien
sûr infini, et il doit être borné de façon appropriée, par exemple en
introduisant une fréquence de coupure aux hautes fréquences. L’énergie du vide
résultante, qui est la somme bornée des énergies des oscillateurs des états de
base de tous les champs de la théorie, n’a aucune raison particulière d’être
nulle et en fait on peut escompter que son facteur d’échelle naturel doit être
du type :
|
|
(75) |
Où la masse de Planck mP est
approximativement 1019 GeV, soit 10-5 grammes. Force est
de constater que les observations de l’Univers à large échelle nous
donnent pour 
, à une valeur qui se révèle plus
petite que ce que prédit (75) par un facteur d’au moins 10120.
Du jamais vu en la matière (si l’on peut dire, s’agissant du vide)!
C’est la discordance la plus importante entre la théorie et l’observation, ce qui fait dire à certains que le problème de la constante cosmologique est un des plus importants problèmes non résolus aujourd’hui.
Pour autant, les observations ne nous assurent pas d’une valeur strictement nulle, ce qui n’est pas sans conséquences sur le destin de l’Univers.
Cette erreur d’Einstein n’en finit pas de traumatiser à la fois et les physiciens qui voudraient comprendre pourquoi elle est si faible et les astronomes qui voudraient savoir si elle est suffisamment petite pour être ignorée.
Des termes de dérivation de
la métrique d’ordre supérieur à deux dans l’action
Une généralisation de l’action de Hilbert moins problématique consiste
à y inclure des scalaires contenant des dérivées de la métrique
d’ordre supérieur à deux. On peut imaginer une action de la forme :
|
|
(76) |
Où les α's sont des constantes de couplage et les points de suspension représentent les autres scalaires qu’on peut construire à partir du tenseur de courbure, ses contractions et ses dérivées. Traditionnellement, de tels termes ont été négligés sur l’argument raisonnable qu’ils compliquent plutôt une théorie dont l’esthétique est appréciée et qui donne des résultats conformes à l’expérience (avec une excellente précision) Trois raisons complémentaires confortent ce peu d’intérêt.
D'abord, le problème des conditions initiales. Comme on va le voir plus loin, dans les équations d’Einstein il suffit juste de connaître les valeurs initiales des coordonnées et de l’impulsion, pour prédire l’évolution du système.
Avec des dérivées d’ordre supérieur, nous nécessitons ces valeurs mais aussi d’autres dont les dérivées de l’impulsion.
Deuxièmement, comme la source principale de frustration pour les physiciens des particules vis-à-vis de cette théorie est qu’elle ne peut pas être “renormalisable” (pour autant qu’on le sache), et que les lagrangiens comportant des dérivées d’ordre supérieur conduisent à des théories qui ne font qu’aggraver cette situation, on imagine leur peu d’enthousiasme pour cette généralisation.
Troisièmement, par les mêmes types d’arguments que ceux développés auparavant lorsque nous avons introduit une constante de couplage entre les champs, pour montrer les limites du principe d’équivalence, les termes supplémentaires de (76) ne sont pas négligeables par rapport au terme de Hilbert habituel, que dans un contexte de très haute énergie (la masse de Planck intervient comme facteur d’échelle naturel) et donc ne sont d’aucune importance pratique dans notre monde de basse énergie.
Aucune de ces raisons n’est vraiment décisive, et certains continuent à explorer cette voie mais sans susciter un gros intérêt.
Champs scalaires
gravitationnels
Une catégorie de modèles qui suscite de l’intérêt est ce qu’on appelle les
théories de la gravitation scalo-tensorielles, du fait qu’elles invoquent et le
tenseur métrique gmn
et un champ scalaire fondamental l.
L’action peut être écrite :
|
|
(77) |
où f () et V() sont des fonctions qui
définissent la théorie
Rappelons que selon (68) le coefficient du scalaire de Ricci en relativité générale classique est proportionnel à l’inverse de la constante de Newton G
Dans les théories scalo-tensorielles, ce coefficient est remplacé par une fonction d’un champ qui peut varier dans l’espace-temps. L’intensité de la gravitation mesurée par la valeur locale de la “constante” de Newton va dépendre du lieu et du temps. En fait la théorie scalaire la plus célèbre, inventée par Brans et Dicke et ainsi nommée s’est inspirée d’une suggestion de Dirac supputant la possibilité de variation de la “constante” de la gravitation dans le temps.
Dirac avait été frappé par des coïncidences
numériques intéressantes qui apparaissent par combinaisons de paramètres
cosmologiques telles que la constante de Hubble H0 (mesure du taux
d’expansion de l’univers) et des paramètres de la physique des particules
comme la masse du pion mπ. Par exemple :
|
|
(78) |
Supposons un instant que cette coïncidence ne soit pas fortuite. Comme la “constante” de Hubble varie dans le temps (dans le modèle cosmologique standard), alors que les autres quantités par convention, ne varient pas, Dirac suggéra que G pourrait varier dans le temps pour conserver la relation (78). Brans et Dicke emboîtèrent le pas à Dirac dans cette voie.
Les expériences que l’on sait réaliser aujourd’hui pour vérifier la Relativité générale sont suffisamment précises pour dire que si la théorie de Brans-Dicke est correcte, la variation de G en fonction de l’espace et du temps qu’elle doit prédire ne peut être que très petite, beaucoup plus petite que ce qu’exigerait la satisfaction de l’Hypothèse de Dirac (voir Weinberg pour les détails sur la théorie de Brans-Dicke et les expériences associées).
Malgré cela une grande effervescence règne dans ce domaine et les domaines connexes, du fait de son importance vitale dans la théorie des supercordes et de ses conséquences permettant de mieux comprendre la physique des tous premiers instants de l’Univers.
Un tenseur de torsion non
nul.
La dernière variante pour la Relativité générale que nous allons mentionner concerne la possibilité que la connexion ne dérive pas de la métrique mais a une existence propre en tant que champ fondamental. À titre de d’exercice, vous pourrez vérifier que l’action que nous avons considérée pour la Relativité générale peut aussi être vue comme et une fonction de la métrique gmn et d’une connexion sans torsion Glrs, et que les équations du mouvement dérivées de la variation de cette action par rapport à la connexion impliquent que Glrs soit le symbole de Christoffel associé à gmn.
Si on lève la contrainte de torsion identiquement nulle, le tenseur de torsion peut apporter quelques degrés de liberté supplémentaires.
Sans rentrer dans les détails, la raison principale qui fait que de telles théories ne suscitent pas beaucoup d’intérêt est que la torsion étant elle même un tenseur, il n’y a rien qui la distingue des autres tenseurs non gravitationnels.
Donc considérer la torsion nulle plus un nombre quelconque de champs tensoriels qu’on peut appeler comme bon nous semble, ce qui est le cas de la Relativité générale, n’entame en rien la généralité de la théorie.
En gardant à l’esprit que l’une de ces possibilités ou plus probablement quelque chose auquel nous n’avons pas encore pensé puisse être effectivement réalisé dans la nature, pour le reste du cours nous nous en tiendrons à la version classique de la Relativité Générale basée sur les équations d’Einstein ou l’action d’Hilbert et nous en tirerons les conséquences.
Solutions de l’équation
d’Einstein
Ces conséquences sont constituées des solutions de l’équation d’Einstein pour diverses sources d’énergie et d’impulsion et le comportement de particules test dans ces solutions.
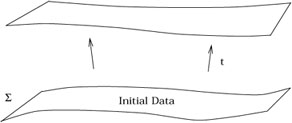
Avant de rentrer dans les détails, regardons de plus près le problème des conditions initiales en Relativité générale.
En mécanique classique de Newton, le comportement d’une particule est régi par
f
= ma. Si la particule est soumise à un potentiel
(champ d’énergie) (x), alors la force est
= -
, et la particule obéit à :
|
|
(79) |
C’est une équation différentielle du deuxième ordre pour xi(t),
qu’on peut réécrire comme un système de deux équations du premier ordre en
introduisant l’impulsion p :
|
|
(80) |
Le problème des valeurs initiales est simplement la procédure spécifiant l’état de départ (xi, pi) qui sert de condition aux limites et pour qui (80) doit avoir une solution unique.
On peut considérer que (80) permet lorsqu’on a
les coordonnées et l’impulsion à l’instant t, d’évoluer de façon
infinitésimale dans le temps vers l’état à t +
t, et par
itération de cette procédure obtenir la solution complète.
Problème des conditions
initiales et de leur évolution en Relativité générale
Essayons de formuler le problème correspondant en Relativité Générale.
Les équations d’Einstein Gmn
= 8GTmn
sont bien sûr covariantes. Elles ne particularisent pas une notion de temps
préférentiel qui servirait de base à l’évolution du système. Cependant nous
pouvons identifier une hypersurface de type espace (une “tranche”)
, spécifier les données initiales sur
cette hypersurface et voir si on peut évoluer uniquement à partir d’elles vers
l’hypersurface du futur.(Hypersurface, car l’espace-temps étant à quatre
dimensions, une tranche d’espace à temps constant, sera à trois dimensions, le
terme surface étant réservé habituellement aux surfaces à deux dimensions).
Ce procédé violente quelque peu la covariance manifeste de la théorie, mais si nous sommes prudents on peut s’en sortir avec une formulation qui est équivalente à résoudre les équations d’Einstein d’un coup pour l’espace-temps
Comme la métrique est
notre variable fondamentale, notre premier propos sera de considérer les
valeurs gmn/
de la métrique sur notre
hypersurface comme les coordonnées et les dérivées par rapport au temps ¶tgmn| (conformément à certaines
coordonnées de temps spécifiées) comme étant l’impulsion, tous deux définissant
l’état. (Il y a aussi des coordonnées et une impulsion pour les champs
matériels que nous ne considérerons pas explicitement.)
En fait les équations Gmn
= 8GTmn
invoquent les dérivées secondes de la métrique par rapport au temps (La
connexion invoque les dérivées premières de la métrique et le tenseur
d’Einstein les dérivées premières de la connexion), donc il semble qu’on soit
sur la bonne voie. Par ailleurs l’identité de Bianchi nous dit que ÑmGmn
= 0.
On peut réécrire cette équation comme suit
|
|
(81) |
Un examen attentif du membre de droite ne révèle aucune dérivée du troisième ordre par rapport au temps, donc il ne peut pas y en avoir dans l’autre membre.
Donc bien que Gmn
dans sa généralité invoque des dérivées secondes par rapport au temps, pas la
composante spécifique G0n. Sur les dix équations correspondant
aux dix composantes indépendantes de l’équation d’Einstein, les quatre
représentées par :
|
|
(82) |
ne peuvent pas être utilisées pour calculer
l’évolution des données initiales (gmn,¶t
gmn).
Contraintes sur les données initiales
Elles sont en fait des contraintes sur les
données initiales. Nous ne sommes pas libres de spécifier n’importe quelle
combinaison de la métrique et de ses dérivées par rapport au temps sur
l’.hypersurface , car elles doivent satisfaire les
relations (82). Les équations restantes :
|
|
(83) |
représentent les équations d’évolution dynamique pour la métrique. Bien sur nous n’avons que six équations pour les dix fonctions inconnues gmn (xs), donc la solution va inévitablement impliquer une quadruple indétermination. Elle correspond aux quatre degrés de liberté que nous avons préalablement évoqués correspondant au choix des quatre fonctions de coordonnées de l’espace-temps.
Creuser (83) pour trouver que toutes les dérivées
secondes par rapport au temps n’apparaissent pas, est un exercice immédiat mais
plutôt laborieux En fait on trouve des termes ¶²tgij
dans (83), mais pas de termes ¶²tg0n.
Donc un "état" en Relativité générale va consister en une
spécification des composantes de type espace de la métrique gij| et de leurs dérivées premières
par rapport au temps ¶tgij| sur l’ hypersurface
, à partir de
laquelle nous allons déterminer la future évolution en utilisant (83), limitée
par une ambiguïté incontournable concernant les composantes g0n.. Cette situation est
précisément analogue à celle de l’électromagnétisme, où nous savons qu’ils n’y
a pas suffisamment de données initiales pour déterminer l’évolution de façon
unique, car il y a toujours la possibilité de réaliser la transformation
de jauge A
A + ¶m.
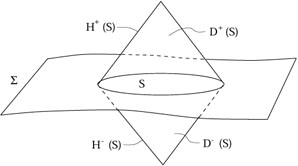
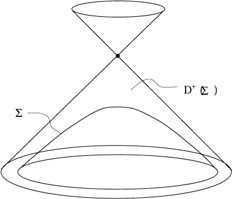
Choix d’une jauge
En Relativité générale, les transformations de coordonnées jouent un rôle qui rappelle celui de la transformation de jauge en électromagnétisme en cela qu’elles introduisent une indétermination dans l’évolution temporelle. Une manière de traiter le problème consiste à choisir une jauge. En électromagnétisme cela signifie fixer une condition sur le potentiel Vecteur Am, qui va contraindre notre liberté de transformation de jauge. Par exemple on peut choisir la jauge de Lorentz qui impose Ñm Am = 0, ou une jauge temporelle où A0 = 0.
On peut faire une chose similaire en Relativité générale en fixant notre
système de coordonnées. Prenons la jauge harmonique (également connue sous le
nom de jauge de Lorentz et quelques autres vocables) qui recueille un large
consensus, elle s’exprime :
|
|
(84) |
Ici =ÑmÑm
est le D'Alembertien covariant, et il est crucial de réaliser que lorsque nous
prenons la dérivée covariante que les quatre fonctions xm ne sont que des
fonctions et pas du tout les composantes d’un vecteur. La condition
est alors :
|
|
(85) |
Dans l’espace Euclidien, les coordonnées
cartésiennes (dans lesquelles Glrs=
0) sont des coordonnées harmoniques. Par principe toute fonction qui
f = 0 est
appelée une fonction harmonique.
Pour vérifier que ce choix de coordonnées fixe bien notre liberté de jauge,
réécrivons la condition (84) sous une forme plus simple. Nous avons
|
(86) |
D’après la définition des symboles de Christoffel. Parallèlement de ¶r
(gmngsn) =¶r
dsm
= 0, nous tirons :
|
|
(87) |
Et, en utilisant le résultat de nos investigations antérieures sur la
variation du déterminant de la métrique (65) nous avons :
|
|
(88) |
En mettant tout cela ensemble, il vient (en général) :
|
|
(89) |
La condition de jauge harmonique (85) est donc équivalente à :
|
|
(90) |
En prenant la dérivée partielle sachant que t = x0
ce qui donne :
|
|
(91) |
Cette condition représente une équation différentielle du deuxième ordre sur les composantes libres de la métrique g0n, en fonction des données initiales fournies. Nous avons donc réussi à fixer les degrés de liberté de jauge et nous pouvons maintenant résoudre l’évolution de la métrique dans sa totalité en coordonnées harmoniques.
Le problème possède toutes
les données nécessaires à sa résolution
Du moins localement, car nous avons discrètement glissé
sur le fait que notre choix de jauge peut ne pas être bien défini globalement,
et que nous pourrions être amenés à travailler sur les “pièces” de la
variété comme d’habitude. Le même problème est présent dans les théories de
jauge de la physique des particules. Remarquons qu’il nous reste quelques
degrés de liberté; notre condition de jauge (84) ne restreint que les
coordonnées qui s’étendent à partir de la surface initiale
à travers l’espace-temps,
mais on peut toujours choisir librement des coordonnées xi
sur . Ceci correspond à la au fait qu’une
transformation de coordonnée xm
xm + dm,
avec dm
= 0, est compatible avec la condition de jauge harmonique.
Nous avons maintenant bien défini les conditions
initiales pour ce problème de Relativité générale, un état est spécifié par ses
composantes d’espace de la métrique et de leurs dérivées par rapport au temps
sur une hypersurface de type espace
; Ceci étant donné
les composantes de type espace (83) des équations d’Einstein nous permettent de
faire évoluer la métrique dans le temps, sous réserve d’une ambiguïté dans le
choix des coordonnées que nous pouvons lever par un choix de jauge. Gardons à
l’esprit que les données de départ ne peuvent pas être arbitraires mais doivent
satisfaire les contraintes (82). Une fois satisfaites sur une hypersurface de
type espace, les équations du mouvement garantissent qu’elles le resteront
comme vous pouvez vérifier.
Ces
contraintes garantissent que le résultat restera covariant dans l’espace-temps
après avoir découpé notre variété selon temps et l’espace. En particulier la
contrainte Gi0 = 8GTi0 implique que
l’évolution est indépendante de notre choix de coordonnées
, alors que G00
= 8GT00 force
l’invariance vis-à-vis des différentes façons de découper l’espace-temps
et en hypersurfaces de type espace :
|
|
Discussion sur l’existence de solutions
Une fois vu comment traiter le problème d’initialisation des équations d’Einstein, un élément d’importance cruciale est l’existence de solutions à ce problème.
Autrement dit, une fois spécifiée une hypersurface de type espace avec ses données initiales, jusqu’à quelle distance un espace-temps unique peut-il être déterminé.
Bien la réponse précise à cette question soit plutôt ardue, il est assez simple d’examiner les conditions de non existence d’une solution bien définie, ce que nous allons faire.
Il est plus simple de
considérer l’évolution de champs de matière dans un cadre fixe, que l’évolution
de la métrique elle-même. Considérons donc une hypersurface de type espace dans une variété M avec
une métrique fixe gmn,
et de surcroît examinons un sous ensemble connecté S dans
. Notre ligne de
conduite sera qu’aucun signal ne se propage plus vite que la lumière, donc
l’information ne va s’écouler que sur des chemins de type temps ou lumière (pas
nécessairement des géodésiques).
Domaines de dépendance
Nous définissons le domaine de dépendance du futur de S, noté D+(S), comme l’ensemble des points p tels que toutes les courbes infinies correspondant à un chemin vers le passé à partir de p coupent S.
Interprétons cette définition de façon à ce que S lui-même soit un sous ensemble de D+(S). (Certes une formulation rigoureuse nous dispenserait d’interprétation supplémentaire sur les définitions, mais soyons maintenant plus rigoureux que nous ne l’avons été par le passé). De même définissons le domaine de dépendance du passé D-(S) de la même manière, mais en remplaçant chemin vers le passé par chemin vers le futur
Généralement certains points de M vont être dans un des domaines de dépendances et d’autres n’y seront pas. Définissons la frontière de D+(S) comme horizon de Cauchy du futur H+(S), et de même la frontière de D-(S) comme l’horizon de Cauchy du passé H-(S). Vous pouvez vous convaincre que les deux sont des surfaces nulles.
|
|
L’utilité de ces définitions saute aux yeux, comme rien ne va plus vite que la lumière, les signaux ne peuvent pas se propager à l’extérieur du cône de lumière associé à p. Donc si chaque courbe qui reste à l’intérieur du cône coupe S, alors l’information spécifié sur S sera suffisante pour prédire quelle sera la situation à p (Les données initiales du champ de matière de S peuvent être utilisées pour calculer la valeur des champs en p)
L’ensemble des points pour lesquels on peut
prédire l’état, en connaissant celui de S est simplement l’union D+(S)
D-(S).
On peut facilement étendre ces idées développées
pour le sous ensemble S à l’hypersurface
dans son intégralité.
Le point important est que D+()
D-() peut ne pas être M dans
son intégralité, même si
lui-même semble être
une hypersurface bien honnête s’étendant à travers l’espace.
Difficultés qu’on peut rencontrer
Cela peut arriver de bien des façons. L’une d’entre elle est de choisir une “mauvaise hypersurface”, encore qu’il soit difficile de dire quand une hypersurface est mauvaise pour cet usage.
Considérons l’espace de Minkowski et une hypersurface de type espace, qui reste dans le passé du cône de
lumière d’un certain point.
|
|
Dans
ce cas est une bonne surface de type espace,
mais il est clair que D+() s’arrête au cône de lumière, et
qu’on ne peut pas utiliser l’information sur pour prédire ce qui se passe dans
l’espace de Minkowski..
Naturellement, nous aurions pu prendre d’autres hypersurfaces dont le domaine de dépendance aurait été la variété en entier. Aussi ceci ne nous traumatise pas trop.
Espace de Misner
Un exemple moins trivial est l’espace de Misner. C’est un espace bi dimensionnel avec la topologie R1× S1, et une métrique pour laquelle le cône de lumière s’incline progressivement au fur et à mesure qu’on avance dans le temps.
|
|
Passé
un certain point, il est possible de voyager sur des trajectoires de type temps
qui s’enroulent autour de S1 et se referment sur
elles-mêmes. On les appelle des boucles temporelles. Si nous avions
spécifié une surface dans le passé de ce point, alors
aucun des points de la région contenant des boucles temporelles n’est dans le
domaine de dépendance de , puisque les boucles
temporelles ne coupent pas . C’est assurément un problème
plus sérieux que le précédent, puisqu’il ne semble pas exister dans ce type
d’espace-temps de solution au problème de prédiction de l’évolution en
partant de valeurs initiales bien définies. À vrai dire les problèmes de ce
type sont toujours en investigation, donc je ne dirai pas que cette énigme est
réglée.
Singularités
Le dernier exemple est fourni par l’existence de singularités, points qui ne sont pas dans la variété, bien qu’ils puissent être atteint en voyageant sur une géodésique sur une distance finie. Typiquement, elles apparaissent quand la courbure devient infinie en un point, si cela arrive, le point ne peut plus être considéré comme appartenant à l’espace-temps. Une telle occurrence peut mener à l’émergence d’un horizon de Cauchy, un point p qui est dans le futur de la singularité ne peut pas être dans le domaine de dépendance d’une hypersurface qui est dans le passé de la singularité, car il y aura des courbes passant par p qui se terminent à la singularité.
|
|
Tous ces obstacles peuvent aussi se produire dans le problème des valeurs initiales en Relativité Générale, quand on essaie de faire évoluer la métrique elle-même depuis des valeurs initiales.
Pourtant il y a différents degrés dans l’horreur.
Synthèse des difficultés
La possibilité de prendre une mauvaise hypersurface n’est pas fréquente, d’autant que la plupart des solutions sont trouvées globalement (en résolvant l’équation d’Einstein pour tout l’espace-temps). Il faut être attentif en cas de résolution numérique de l’équation d’Einstein où un mauvais choix d’hypersurface peut conduire à des calculs inextricables même si en principe une solution complète existe.
La Relativité générale s’efforce d’éviter les boucles temporelles, il y a sûrement des solutions qui les incluent mais elles ne résultent pas d’une évolution à partir de données initiales.
Les singularités sont par contre incontournables. Le simple fait que la gravitation soit toujours attractive génère une concentration de matière, augmentant la courbure et qui peut dégénérer en une singularité.
Il faut apprendre à vivre avec, d'autant qu’on peut espérer qu’une théorie quantique de la gravitation bien définie pourra éliminer les singularités de la Relativité Générale “classique”