-
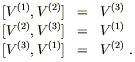
(1)
Original : http://pancake.uchicago.edu/~carroll/notes/ : Ce document est la traduction (avec la permission de l’auteur) du chapitre 7 de " Lecture notes on General relativity" de Sean. M. Carroll. J. Fric endosse toute responsabilité pour les erreurs que sa traduction (qui n’a pas été vérifiée par l’auteur) aurait pu ajouter. En cas de doute, veuillez vous rapporter à la version originale.
Chapitre 7 : Les trous noirs sphériques, sphériques chargés et en rotation.
Table des matières
Métrique de Schwarzschild 4
Métrique à symétrie sphérique 4
Vecteurs de Killing 4
Exemple d’espace temps à symétrie sphérique 5
Forme générale d’une métrique à symétrie sphérique 6
Forme générale d’un espace temps à quatre dimensions à symétrie sphérique 7
Métrique à symétrie sphérique particulière : Cas de la Relativité générale 9
Calcul des symboles de Christoffel non nuls 9
Calcul des composantes non nulles du tenseur de Riemann 9
Calcul des composantes non nulles du tenseur de Ricci : 9
Forme intermédiaire de la métrique 10
Vecteur de Killing de type temps associé à la métrique 10
Métrique stationnaire 11
Métrique statique 11
Forme quasi définitive de la métrique à symétrie sphérique relativiste 12
La limite de la métrique à l’infini 12
Le résultat final : la métrique de Schwarzschild. 13
Singularités de la métrique 13
Singularités de coordonnées, singularités vraies 13
Critère de singularité vraie 14
La singularité à r = 0 est une vraie singularité 14
La singularité à r = 2GM est une singularité de coordonnées 14
Cas de r £ 2GM 14
Équation géodésique en métrique de Schwarzschild 15
Résolution indirecte de l’équation géodésique par les vecteurs de Killing 16
Invariants associés aux vecteurs de Killing 16
Invariant métrique 16
Signification des invariants 16
Invariance dans le temps : conservation de l’énergie 16
Invariance dans l’espace : conservation du moment cinétique 17
Orbites des particules en métrique de Schwarzschild 17
Équation géodésique : forme 1 18
Équation géodésique : forme 2 18
“Potentiel” gravitationnel en Relativité Générale en métrique de Schwarzschild 18
Trajectoires typiques 18
Comparaison avec la mécanique Newtonienne 18
Influence du terme supplémentaire de la métrique de Schwarzschild 19
Conditions associées à une orbite circulaire 19
Cas mécanique Newtonienne 19
Cas Relativité générale 20
Synthèse sur les orbites circulaires 22
Validation expérimentale de la Relativité générale 22
La précession du périhélie de Mercure 22
Décalage vers le rouge en métrique de Schwarzschild 23
Autres tests de la Relativité générale 25
Pulsar binaire 25
Effet Shapiro 25
Entraînement du référentiel de Lense-Thirring. 25
Géométrie des trous noirs 25
Où à nouveau il est question de la pseudo-singularité à r = 2GM 26
Comment effacer la pseudo-singularité par un changement de coordonnées ? 27
Coordonnées de Eddington-Finkelstein 28
L’Horizon événementiel 29
Première extension du domaine de la variété accessible par la métrique 30
Recherche de la forme d’extension maximum 30
Finalisation du changement de coordonnées 31
Le but recherché : les coordonnées de Kruskal 32
Diagramme de Kruskal 33
Régions définies par le diagramme de Kruskal 34
La nature étrange de l’espace temps des trous noirs révélée par ces coordonnées 35
Trous de ver 36
Diagramme de Kruskal d’un trou noir astrophysique résultant d’un effondrement stellaire 37
Formation des trous noirs astrophysiques 37
Diagramme de Penrose 38
Diagramme de Penrose de l’espace de Minkowski 38
Métrique Minkowski " conforme" avec coordonnée temporelle h et coordonnée spatiale c 41
Représentation de Penrose de la métrique de Minkowski 41
Diagramme de Penrose de la métrique de Minkowski en coordonnées cylindriques 42
Diagramme de Penrose de la métrique de Minkowski en coordonnées planes 42
Diagramme de Penrose d’un trou noir de Schwarzschild 43
Diagramme de Penrose relatif à l’effondrement d’une étoile en trou noir 45
Les trous noirs sont imberbes 45
L’évaporation des trous noirs, le rayonnement de Hawking 45
Le mystère de la perte d’information dans les trous noirs 46
Trous noirs statiques électriquement chargés 47
Métrique générique des trous noirs statiques chargés 47
Le tenseur énergie-impulsion de la charge 47
Métrique de Reissner-Nordstrøm 48
Singularités en métrique de Reissner-Nordstrøm 49
Singularité vraie 49
Singularité de coordonnées 49
Métrique du premier type : GM2 < p2 + q2 50
Singularité nue : Trous noirs chargés de type 1 : Pas d’horizon des événements 50
Diagramme de Penrose pour trou noir statique chargé de type 1 50
Conjecture de censure Cosmique 51
Réalité physique de tels trous noirs 51
Trous noirs statiques chargés de type 2 : GM2 > p2 + q2 51
Trous noirs chargés de type 2 : les deux Horizons 51
Diagramme de Penrose des trous noirs de type 2 52
Voyage dans les univers miroirs des trous noirs de type deux 52
L’horizon extérieur 52
L’horizon intérieur 53
Les fontaines blanches (trous blancs) 53
Réalité physique de tels trous noirs 53
Trous noirs statiques chargés de type trois : GM2 = p2 + q2 53
Diagramme de Penrose pour trou noir statique chargé de type trois 54
L’horizon double se comporte comme pas d’horizon 54
Trous noirs en rotation 54
Établissement de la métrique 54
La métrique de Kerr 55
La métrique de Kerr-Newman 55
Les coordonnées de Boyer-Lindquist 55
Les vecteurs de Killing sont de nouveau d’un grand secours 56
Un tenseur de Killing en renfort 56
Les trois types de trous noirs en rotation 57
Singularités : Les horizons d’un trou noir en rotation de type 1 58
Horizons extérieur et intérieur des événements 58
Une hypersurface remarquable : L’hypersurface où le vecteur de Killing ∂t, de type temps s’annule 59
L’ergosphère 59
La vraie singularité a la forme d’un anneau 60
Voyage au travers de l’anneau singulier 60
Diagramme de Penrose des trous noirs en rotation 60
61
La machine à remonter le temps 61
Réalité physique de telles solutions 62
Du bon usage de l’ergosphère 62
Définition de la vitesse angulaire du trou noir 62
Entraînement du référentiel par le trou noir en rotation 63
Mouvement géodésique dans l’ergosphère 63
Extraction d’énergie d’un trou noir en rotation : Le procédé de Penrose 64
On ne peut extraire que de l’énergie du moment cinétique du trou noir en le ralentissant 66
On ne peut pas faire décroître l’aire de l’horizon des événements 66
La masse irréductible d’un trou noir en rotation 67
On peut extraire jusqu’à 29% de l’énergie d’un trou noir jusqu’à provoquer son arrêt 67
Gravité de surface du trou noir 68
Analogie avec la thermodynamique 68
Température du trou noir 68
Entropie du trou noir 69
Zéro absolu et censure cosmique 69
Nous quittons le domaine des solutions dans la limite en champ faible pour explorer celui des solutions générales non linéaires de l’équation d’Einstein. Si on excepte l’espace de Minkowski, la solution générale la plus importante est celle établie par Schwarzschild qui décrit les espaces temps vides à symétrie centrale. Comme nous sommes dans le vide, l’équation d’Einstein s’écrit Rmn= 0.
Puisque nous avons une proposition de solution au jeu d’équations différentielles, il nous suffirait de l’appliquer pour la vérifier, mais nous voudrions faire mieux.
En fait nous allons esquisser une preuve du théorème de Birkhoff, qui stipule que la solution de Schwarzschild est la seule solution aux équations d’Einstein dans le vide correspondante à une symétrie sphérique.
La démarche va d’abord s’appuyer sur une argumentation intuitive non rigoureuse relative à la forme que doit prendre une métrique à symétrie sphérique, qu’elle soit ou ne soit pas solution de l’équation d’Einstein et à partir de là déduire méthodiquement la bonne solution dans ce cas.
La symétrie sphérique est caractérisée par la symétrie de la sphère (dans ce contexte, il s’agit de sphère S² classique). Comme notre recherche porte sur la métrique d’une variété différentiable, nous allons nous intéresser à celles qui possèdent cette symétrie. Nous savons que les symétries, d’une métrique, sont caractérisées par l’existence de vecteurs de Killing.
Plus, nous connaissons les vecteurs de Killing associés à S². Il y en a trois. Donc une variété à symétrie sphérique aura trois vecteurs de Killing, juste comme ceux de la sphère S². Nous voulons dire par-là que le commutateur des vecteurs de Killing sera le même dans les deux cas, soit en langage plus savant que l’algèbre générée par les vecteurs sera la même. Quelque chose que nous n’ayons pas montré, mais qui est vrai, est que nous pouvons choisir nos trois vecteurs de Killing de S²(V(1), V(2), V(3)), tels que :
|
|
(1) |
Les relations des commutations sont celles de SO(3), le groupe des rotations en trois dimensions.
Ce n’est pas une coïncidence, mais nous ne développerons pas ce point. Ce qui nous intéresse c’est qu’une variété à symétrie sphérique doit posséder trois champs de Vecteurs de Killing obéissant aux relations ci-dessus.
Auparavant nous avions mentionné le théorème de Frobénius, qui dit que si nous avons un ensemble de champs vectoriels qui commutent, alors il existe un jeu de fonctions de coordonnées tels que ces champs de vecteurs en sont les dérivées partielles. (En fait le théorème ne s’arrête pas là mais stipule que si on a des champs de vecteurs qui ne commutent pas, mais dont le commutateur “ferme”, le commutateur de deux champs quelconques dans l’ensemble est une combinaison linéaire d’autres champs dans l’ensemble, alors les courbes intégrales de ces champs de vecteurs, s’assemblent pour décrire une sous variété de la variété dans laquelle ils sont tous définis).
La dimension de la sous variété peut être inférieure ou égale au nombre de vecteurs, mais évidemment pas supérieure.
Les champs de Vecteurs qui satisfont (1) vont bien sûr générer des sphères S².
Comme les champs de vecteurs s’étendent à travers l’espace, chaque point va être exactement sur une de ces sphères. (Nous devrions dire presque tous les points, car nous allons voir plus loin, comment il peut y avoir des exceptions). Alors nous dirons que la variété à symétrie sphérique peut être foliotée en sphères.
Redescendons sur terre et considérons l’exemple le plus simple de l’espace Euclidien tridimensionnel.
Si on choisit une origine alors R3 présente manifestement une symétrie sphérique par rapport aux rotations ayant pour centre cette origine. Par ces rotations (c.a.d par le flux des champs de vecteurs de Killing), les points se transforment en restant sur la même Sphère S² à distance fixe de l’origine.
|
|
Ce sont ces sphères qui stratifient tout R3 sauf le centre de symétrie qui reste invariant sous ces rotations. L’espace est donc pratiquement complètement stratifié en sphères concentriques autour de son origine, ce qui est de nature à nous satisfaire.
Il existe des solutions à symétrie sphérique qui ne possèdent pas d’origine autour de laquelle on réalise les rotations. Le “trou de ver” de topologie R x S² en est un exemple. Il est représenté ci-dessous avec une dimension de moins S² -> S.
Dans ce cas, la foliation de la variété tout entière en sphères est réalisable, sans point “singulier”.
La découpe en couches concentriques suggère de structurer les coordonnées de la variété. C’est-à-dire structurer notre variété de dimension n, en tenant compte des symétries de la sous variété de dimension m. Nous utiliserons un jeu de m fonctions de coordonnées ui dans la sous variété, et un jeu de n - m fonctions des coordonnées vI pour repérer la sous variété concernée (i de 1 à m, I de 1 à n-m). La combinaison de ces deux jeux de sous-coordonnées permet de baliser la variété entière. Si la sous variété est à symétrie spatiale maximum (ce qui est le cas des sphères), nous pouvons utiliser le théorème qui stipule qu’il est possible de choisir les coordonnées u de telle sorte que la métrique de la variété complète soit de la forme :
|
|
(2) |
Dans cette expression, gij (u) est la métrique de la sous variété. Ce théorème nous enseigne deux choses : Il n’y a pas de termes croisés dvIduj, et gIJ(v) et f (v) sont, tous deux, fonction de vI seulement, indépendants des ui. Démontrer le théorème est plutôt laborieux, mais les courageux sont invités à consulter le chapitre 13 de Weinberg. Néanmoins c’est un résultat très probant. En gros, la symétrie du problème nous a permis de séparer les variables. Les coefficients de la métrique gIJ(v) et f (v) sont invariants vis-à-vis de ui, quand on se déplace dans la sous variété à coordonnées vI constantes, du fait de la symétrie.
Les termes croisés, peuvent être évités
en choisissant les vecteurs tangents
![]() /
/![]() vI orthogonaux à la sous variété,
ce qui veut dire, en d’autres termes, que nous avons bien
découpé nos sous variétés de la même
manière partout dans l’espace.
vI orthogonaux à la sous variété,
ce qui veut dire, en d’autres termes, que nous avons bien
découpé nos sous variétés de la même
manière partout dans l’espace.
Maintenant que nous avons fini ces considérations
formelles, nous pouvons commencer nos calculs. Dans notre cas, les
sous variétés sont des sphères. Nous sommes donc
amenés naturellement à choisir les coordonnées
sphériques (![]() ,F) dans lesquelles la métrique
prend la forme :
,F) dans lesquelles la métrique
prend la forme :
|
|
(3) |
Comme nous nous intéressons à un espace temps à quatre dimensions, nous nécessitons deux coordonnées additionnelles que nous appellerons a et b. Le théorème (2) nous indique que la métrique d’un espace temps à symétrie sphérique peut être mise sous la forme :
|
|
(4) |
Où r(a, b) est une fonction pas encore déterminée à laquelle nous avons juste donné un nom prémonitoire. Nous pouvons ad libitum changer les coordonnées (a, b) en (a, r), en inversant r(a, b) puisque r n’est pas une fonction de a seul. Nous pourrions tout aussi bien le permuter avec (b, r), compte tenu du rôle symétrique de a, b. Nous ne considérerons pas cette situation séparément. La métrique est alors :
|
|
(5) |
La prochaine étape consiste à trouver une fonction t(a, r) telle que dans le système de coordonnées (t, r) il n’y ait pas de termes croisés dtdr + drdt dans la métrique.
Remarquons que :
|
|
(6) |
Donc :
|
|
(7) |
Nous aimerions remplacer les trois premiers termes de la métrique (5) par :
|
|
(8) |
Pour des fonctions de m et n. Ceci est équivalent aux conditions :
 (9)
(9)
|
|
|
|
|
(10) |
et
|
|
(11) |
On obtient ces équations en calculant m.dt² + n.dr² à partir de (7) et en identifiant à (5) les coefficients de (da², da.dr+dr.da, dr²)
Cela fait trois équations pour les trois inconnues t(a, r), m(a, r), et n(a, r), ce qui suffit à notre bonheur (sous réserve des conditions initiales pour t). Certes elles sont déterminées par rapport aux autres fonctions gaa, gar, et grr, inconnues elles-mêmes, donc à ce titre restent indéterminées. Pourtant cela ne nous empêche pas de poser notre métrique comme étant de la forme :
|
|
(12) |
À ce point, la seule différence entre les deux coordonnées t et r est que nous avons choisi r comme le coefficient multiplicateur de la métrique de la sphère. Le choix était motivé par notre connaissance de la métrique de Minkowski qui s’écrit : ds2 = - dt2 + dr2 + r2dW². Nous savons que l’espace temps que nous considérons est Lorentzien, donc soit m soit n est négatif.
Choisissons m, coefficient de dt² négatif. Ce choix est arbitraire et peut se révéler inapproprié, mais assumons-le pour l’instant.
Cette assertion n’est pas absurde, du fait que l’espace de Minkowski possède lui-même une symétrie sphérique et peut donc être décrit par (12).
Ce choix étant fait, changeons les fonctions m, n en a,b de sorte que :
|
|
(13) |
C’est la forme la plus achevée que nous pouvons tirer des seules considérations de symétrie de l’espace.
Pour particulariser cette métrique dans le
cadre de la Relativité Générale, nous devons
maintenant résoudre les équations d’Einstein
qui vont nous permettre de déterminer les fonctions
![]() (t,
r) et b(t, r).
(t,
r) et b(t, r).
On ne coupe pas à calculer les symboles de Christoffel avec la métrique (13) nécessaires au calcul du tenseur de Courbure et de là, du tenseur de Ricci. Si on désigne par les indices (0,1,2,3) les coordonnées (t, r, q, F) de façon classique, alors les symboles de Christoffel sont donnés par :
|
|
(14) |
Les symboles ne figurant pas explicitement sont supposés égaux à zéro ou implicitement désignés par symétrie.
Les composantes non nulles du tenseur de Riemann sont alors :
|
|
(15) |
En le contractant comme d’habitude, on obtient les composantes non nulles du tenseur de Ricci :
|
|
(16) |
Étant dans le vide, toutes les composantes du tenseur de Ricci sont nulles (Rmn = 0). De R01 = 0, nous tirons :
|
|
(17) |
Si nous considérons la dérivée par rapport au temps de la composante R22, elle est nulle. (car R22= 0). En utilisant ¶0b= 0, nous tirons aisément :
|
|
(18) |
Nous pouvons alors écrire :
|
|
(19) |
Le premier terme de la métrique (13) est
alors - e2f(r)e2g(t)dt2.
Mais nous pouvons redéfinir notre coordonnée de temps
en remplaçant dt
![]() e-g(t)dt,
nous sommes en effet libres de choisir t de sorte que g(t)
=0, d’où
e-g(t)dt,
nous sommes en effet libres de choisir t de sorte que g(t)
=0, d’où
![]() (t,
r) = f (r). nous avons donc
(t,
r) = f (r). nous avons donc
|
|
(20) |
Toutes les composantes de la métrique sont indépendantes de la coordonnée t. Nous venons de prouver un résultat crucial :
Toute métrique du vide à symétrie sphérique possède un vecteur de Killing de type temps.
Cette propriété est tellement importante qu’elle a son propre nom.
Une métrique qui possède un vecteur de Killing de type temps est appelée stationnaire.
Il y a une propriété encore plus restrictive : Une métrique est appelée statique si elle possède un vecteur de Killing de type temps qui est orthogonal à une famille d’hypersurfaces. Une hypersurface d’une variété à n dimensions est simplement une sous variété à (n-1) dimensions.
La métrique de (20) n’est pas seulement stationnaire, elle est aussi statique, le champ de vecteurs de Killing ¶0 est orthogonal aux surfaces t = constante (du fait de l’absence de termes croisés dtdr)
En résumé, dans une métrique statique, rien ne bouge alors que dans une métrique stationnaire les choses peuvent bouger, mais en conservant la symétrie sphérique. Par exemple une métrique à symétrie statique va décrire des étoiles ou des trous noirs qui ne sont pas en rotation alors que les mêmes systèmes en rotation vont être décrits par une métrique stationnaire.
Encore que les mots soient assez clairs, ils peuvent prêter à confusion, mais la distinction entre les deux concepts est compréhensible.
Continuons dans notre recherche de la solution précise.
Comme R00 et R11 s’annulent on peut écrire :
|
|
(21) |
Ce qui implique
![]() =
- b+ constante. Nous
pouvons nous débarrasser de la constante par ajustement des
coordonnées, donc nous avons :
=
- b+ constante. Nous
pouvons nous débarrasser de la constante par ajustement des
coordonnées, donc nous avons :
|
|
(22) |
Penchons-nous sur R22 = 0, il devient :
|
|
(23) |
Ceci est équivalent à :
|
|
(24) |
On peut le résoudre et on obtient :
|
|
(25) |
Où m est une constante indéterminée. Avec (22) et (25) notre métrique devient :
|
|
(26) |
Tous les paramètres ont été fixés sauf la constante m. Nous pouvons vérifier que cette forme satisfait les équations restantes R00 = 0 et R11 = 0, quel que soit m
Il reste à donner une signification physique à m. Le cas le plus important d’utilisation de cette métrique à symétrie sphérique est la représentation de l’espace temps autour (à l’extérieur) d’une étoile, d’une planète.
Dans ce cas on doit retrouver les conditions de
champ faible à l’infini quand r
![]()
![]() .
Dans cette limite (26) implique :
.
Dans cette limite (26) implique :
|
|
(27) |
La limite en champ faible vaut par ailleurs :
|
|
(28) |
avec le potentiel gravitationnel
![]() =
- GM/r.
=
- GM/r.
Comme la métrique doit tendre vers cette limite nous devons poser : m = - 2GM.
Le résultat final est alors la célèbre métrique de Schwarzschild.
|
|
(29) |
Elle est valable pour n’importe quelle
solution à symétrie sphérique dans le vide de
l’équation d’Einstein, M étant un paramètre
qui doit être interprété comme la masse
conventionnelle en mécanique Newtonienne qu’on
peut mesurer en étudiant les orbites à grande distance
de la source gravitationnelle. Quand M
![]() 0
nous retrouvons la métrique de Minkowski comme escompté.
Remarquons que quand r
0
nous retrouvons la métrique de Minkowski comme escompté.
Remarquons que quand r
![]()
![]() ,
nous retrouvons asymptotiquement également cette métrique.
Cette propriété est appelée courbure nulle
asymptotique.
,
nous retrouvons asymptotiquement également cette métrique.
Cette propriété est appelée courbure nulle
asymptotique.
Le théorème de Birkhoff stipule que non seulement la métrique de Schwarzschild est une bonne solution, mais que c’est la seule. Il est intéressant de noter que le résultat est une métrique statique alors que nous n’avons rien imposé à la source sinon la symétrie sphérique. En particulier, nous n’avons pas imposé que la source soit elle-même statique, cela peut donc être une étoile en cours d’effondrement sous réserve que cet effondrement préserve la symétrie sphérique. Ainsi un événement tel que l’explosion d’une supernova typiquement à symétrie sphérique devrait générer très peu d’ondes gravitationnelles, eu égard à l’énergie considérable libérée par ailleurs. Nous avons le même résultat en électromagnétisme pour les champs générés par des distributions de charges à symétrie sphérique qui ne dépendent pas de la distribution radiale
Avant d’étudier le comportement de particules de test dans la géométrie de Schwarzschild, nous devons parler des singularités. De la forme de la métrique (29), on voit que les coefficients deviennent infinis pour r = 0 et r = 2GM : Un signe plutôt inquiétant.
Mais les coefficients de la métrique
dépendent des coordonnées, nous devons donc examiner
leur comportement avec circonspection.. Il est possible de rencontrer
des singularités de coordonnées qui résultent
d’une discontinuité de la coordonnée mais pas de
la variété où elle s’applique. Un exemple
classique est celui de l’origine en coordonnées polaires
planes où la métrique ds2 = dr2
+ r2dq²
dégénère et où la composante g![]()
![]() =
r-2 de la métrique inverse explose, même
si ce point ne diffère en rien des autres dans la variété.
=
r-2 de la métrique inverse explose, même
si ce point ne diffère en rien des autres dans la variété.
Quel indicateur indépendant des coordonnées pourrait nous signaler une singularité de la géométrie? Cette question n’a pas de réponse simple et des livres entiers ont été écrits sur la nature des singularités en Relativité Générale. Sans rentrer dans les détails, un critère simple qui caractérise un problème sérieux est une courbure qui devient infinie. Nous savons quelle est mesurée par le tenseur de Riemann et il n’est pas simple de dire quand un tenseur diverge, car ses composantes dépendent des coordonnées. Mais nous pouvons construire des scalaires à partir du tenseur de courbure et comme les scalaires ne dépendent pas des coordonnées il sera instructif de considérer leur comportement.
Le plus simple est une vielle connaissance :le scalaire de Ricci R = gmnRµn , mais on peut en construire d’ordre supérieur tels que Rmn. Rµn , Rmnrs. Rµnrs , etc. Si l’un de ces scalaires (pas nécessairement tous) tend vers l’infini quand nous approchons un certain point, cela sent la singularité. Il faut aussi vérifier que ce point est à distance fini, qu’il peut être atteint au terme d’un voyage de distance finie sur une courbe. Nous avons là une condition suffisante de définition de singularité, mais pas de condition nécessaire. Comme c’est difficile de montrer qu’un point donné n’est pas singulier, pour notre propos nous allons étudier si une géodésique se comporte bien au point en question et si oui, nous considérerons le point non singulier. Dans le cas de la métrique de Schwarzschild (29), le calcul direct révèle que :
|
|
(30) |
Cela suffit à nous convaincre que r = 0 est une vraie singularité.
Mais pour, r = 2GM, rien de compromettant ne se passe, nous en concluons que cette pseudo-singularité résulte d’un choix inapproprié des coordonnées. Il nous reste à opérer une transformation pour travailler avec des coordonnées appropriées, si c’est possible. Nous verrons bientôt que oui et que la surface r = 2GM se comporte régulièrement (quoiqu’elle présente quelques particularités intéressantes) dans la métrique de Schwarzschild.
Ayant éclairci ce problème de singularités, faisons remarquer que ce qui se passe à r £ 2GM mérite qu’on s’y attarde un petit peu. La solution que nous avons établie n’est valide que dans le vide et nous supposons qu’elle s’applique à l’extérieur d’un corps sphérique tel qu’une étoile. Dans le cas du Soleil ceci concernerait une étoile d’un rayon de :
|
|
(31) |
Mais, r = 2GMsoleil est bien à l’intérieur du soleil où la métrique de Schwarzschild ne s’applique pas. En fait les solutions réalistes à l’intérieur d’une étoile, sont de la forme :
|
|
(32) |
Voir Schutz pour les détails. Ici m(r) est une fonction de r qui tend vers zéro plus vite que r lui-même, donc nous n’avons pas de singularités à r = 0 dans ce cas. Cependant il y a des objets, comme les trous noirs, pour qui la métrique de Schwarzschild complète est requise. Laissons donc notre imagination vagabonder bien loin de notre système solaire pour considérer ce qui suit.
Pour comprendre cette métrique étudions le comportement des géodésiques. Calculons les symboles de Christoffel non nuls pour cette métrique de Schwarzschild :
|
|
(33) |
L’équation géodésique
va être représentée par ces quatre équations
ou
![]() est
un paramètre affine :
est
un paramètre affine :
|
|
(34) |
|
|
(35) |
|
|
(36) |
et
|
|
(37) |
À première vue, il n’y a pas beaucoup d’espoir de résoudre simplement ce jeu d’équations couplées.
Mais notre tâche va se simplifier sérieusement du fait du haut degré de symétrie de la métrique de Schwarzschild. Nous savons qu’il y a quatre vecteurs de Killing, trois pour la symétrie sphérique et un pour les translations dans le temps.
Chacun d’eux correspond à une constante du mouvement pour une particule libre. Si Km est un vecteur de Killing nous savons que :
|
|
(38) |
De plus, il y a une autre constante associée au mouvement sur une géodésique. La compatibilité avec la métrique implique que le long de la trajectoire la quantité :
|
|
(39) |
est constante. Naturellement pour une particule
massive nous choisirons
![]() =
=
![]() ,
et cette relation devient
,
et cette relation devient
![]() =
- gmnUmUn
= + 1. Pour une particule sans masse nous aurons toujours
=
- gmnUmUn
= + 1. Pour une particule sans masse nous aurons toujours
![]() =
0. Considérons aussi le cas de géodésiques de
type espace (bien qu’elles ne correspondent pas à des
chemins pour des particules), pour elles nous choisirons
=
0. Considérons aussi le cas de géodésiques de
type espace (bien qu’elles ne correspondent pas à des
chemins pour des particules), pour elles nous choisirons
![]() =
- 1.
=
- 1.
Plutôt que d’écrire maintenant les expressions explicites des quatre quantités conservées associées aux vecteurs de Killing, penchons-nous sur leur signification. Remarquons que les symétries qu’elles représentent sont aussi présentes dans l’espace temps de Minkowski, où les quantités conservées en question sont bien connues.
L’invariance dans le temps conduit à la conservation de l’énergie, tandis que les trois invariances sous les trois rotations d’espace conduisent à la conservation des trois composantes du moment cinétique. Ceci s’applique également dans la métrique de Schwarzschild.
Au moment cinétique sont associés les trois vecteurs d’espace, l’un représente l’amplitude et les deux autres la direction. La conservation de la direction signifie que la particule se meut dans un plan que nous pouvons choisir comme étant le plan équatorial de notre système de coordonnées.
Si une particule n’est pas dans ce plan, nous pouvons opérer une rotation sur les coordonnées jusqu’à ce qu’elle y soit.
Donc les deux vecteurs de Killing qui conduisent à la conservation de la direction du moment cinétique impliquent :
|
|
(40) |
Les deux vecteurs restants correspondent à l’énergie et à l’amplitude du moment cinétique. L’énergie provient du vecteur de Killing de type temps K = ¶t, soit :
|
|
(41) |
Le vecteur de Killing contrôlant la conservation de l’amplitude du moment cinétique est L = ¶F, soit :
|
|
(42) |
Comme (40) implique sin![]() = 1 sur les géodésiques qui nous intéressent,
les deux quantités conservées sont alors (cf 38) :
= 1 sur les géodésiques qui nous intéressent,
les deux quantités conservées sont alors (cf 38) :
|
|
(43) |
et
|
|
(44) |
Pour les particules sans masse on peut les interpréter comme l’énergie et le moment cinétique. Pour les particules massives elles seront l’énergie et le moment cinétique par unité de masse de la particule. À noter que l’invariance de (44) correspond à la deuxième loi de Kepler (Aires égales balayées dans des temps égaux).
Ensemble, ces quantités conservées
nous procurent un moyen convenable pour comprendre les orbites des
particules dans la géométrie de Schwarzschild.
Développons l’expression (39) pour
![]() on
obtient :
on
obtient :
|
|
(45) |
Si nous multiplions ceci par (1 - 2GM/r) et utilisons nos expressions de E et L, nous obtenons :
|
|
(46) |
Notre équation unique en r(![]() )
est un réel progrès, si nous considérons le
système complexe d’équations couplées du
départ, mais elle peut avoir encore meilleure allure écrite
comme.
)
est un réel progrès, si nous considérons le
système complexe d’équations couplées du
départ, mais elle peut avoir encore meilleure allure écrite
comme.
|
|
(47) |
où
|
|
(48) |
L’équation (47) est précisément celle du mouvement classique d’une particule de masse unité et d’énergie 1/2(E²) dans un potentiel unidimensionnel défini par V(r), (l’énergie réelle de la particule par unité de masse est E, mais le potentiel effectif pour la coordonnée r est en rapport avec ½ E²).
Notre situation est un peu différente de celle du mouvement classique.
Les trajectoires considérées sont des orbites autour d’une étoile ou tout autre corps massif
Nous nous intéressons non seulement aux
relations r(![]() ),
mais aussi à t(
),
mais aussi à t(![]() )
et f (
)
et f (![]() ).
Cependant, il n’est pas évident de bien comprendre la
structure des orbites uniquement à partir du comportement de
leur rayon, il est donc très instructif de nous ramener à
un problème que nous savons résoudre.
).
Cependant, il n’est pas évident de bien comprendre la
structure des orbites uniquement à partir du comportement de
leur rayon, il est donc très instructif de nous ramener à
un problème que nous savons résoudre.
Les similitudes avec la gravitation Newtonienne que révèle la forme de (47) vont nous aider. La différence dans notre cas réside dans l’expression du potentiel (48) ou nous avons un terme supplémentaire. Notons que notre équation est exacte, elle n’est pas une approximation en série de 1/r.
Dans le potentiel décrit par (48), le premier terme est une constante, le deuxième terme correspond exactement au potentiel Newtonien, le troisième terme est une contribution du moment cinétique qui prend la même forme en gravitation Newtonienne et en Relativité Générale.
Le dernier terme en 1/r3, propre à la Relativité Générale fait toute la différence surtout quand r est petit
Regardons les différents types possibles d’orbites illustrés sur la figure. Il y a différentes courbes V(r) correspondant aux différentes valeurs de L. Pour chacune de ces courbes le comportement de l’orbite peut s’évaluer en comparant 1/2(E²) à V(r).
Sous l’effet du potentiel, la particule va se rapprocher de la source de gravitation et lorsque le potentiel s’est réduit à V(r) = 1/2(E2), elle recommence à s’en éloigner. Selon les cas la particule peut s’échapper, sa trajectoire étant simplement déviée ou elle peut être capturée par la source de gravitation orbitant alors autour d’elle. L’orbite peut être circulaire rc = constante, si cela arrive le potentiel est constant, dV/dr = 0.
En différenciant (48), nous trouvons que les conditions associées à une orbite circulaire sont :
|
|
(49) |
où g= 0 en gravitation Newtonienne et g= 1 en Relativité Générale. Les orbites circulaires sont stables si elles correspondent à un minimum du potentiel et instable si elles correspondent à un maximum. Les orbites captives qui ne sont pas circulaires vont osciller autour du rayon de l’orbite circulaire stable.
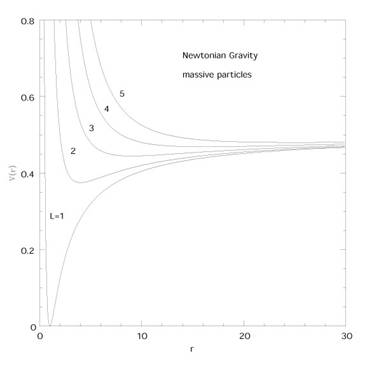
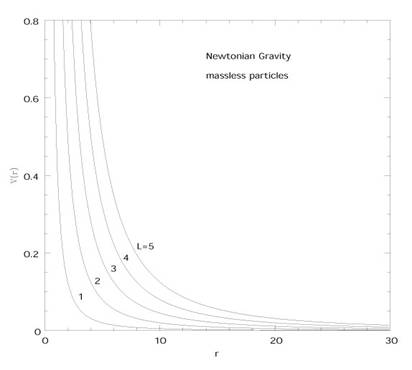
En gravitation Newtonienne, les orbites circulaires sont définies par :
|
|
(50) |
Pour les particules sans masse, il n’existe pas d’orbite circulaire, c’est conforme à la figure, qui montre qu’il n’y a pas d’orbites captives quelles qu’elles soient. Bien que ce ne soit pas évident dans ce système de coordonnées, les particules sans masse se meuvent en ligne droite en mécanique Newtonienne, la force sur une masse nulle valant zéro (Glissons sur le problème de la particule de masse nulle en mécanique Newtonienne).
Un photon d’énergie E venant de r
=
![]() va
progressivement "ralentir " (en fait dr/d
va
progressivement "ralentir " (en fait dr/d![]() va décroître sans que cela ne change la vitesse de la
lumière) jusqu’au point le plus près et puis il
va s’éloigner de nouveau vers r =
va décroître sans que cela ne change la vitesse de la
lumière) jusqu’au point le plus près et puis il
va s’éloigner de nouveau vers r =
![]() .
.
Les valeurs les plus basses de L pour lesquelles le photon se rapproche puis s’éloigne, sont celles correspondant aux trajectoires qui se dirigeaient initialement au plus près du corps générant le champ.
Pour les particules massives ces trajectoires vont être des orbites circulaires stables de rayon (50) ou des orbites captives qui vont osciller autour de ce rayon. Si l’énergie est supérieure à la valeur asymptotique E=1, les orbites seront non captives, la particule s’approchant puis s’éloignant indéfiniment. Nous savons qu’en mécanique Newtonienne, ces orbites sont des sections coniques. Les orbites captives sont soit des cercles soit des ellipses, tandis que les orbites non captives sont des hyperboles ou paraboles (nous ne le montrerons pas ici).
En Relativité générale il en va
tout autrement mais seulement pour les faibles valeurs de r.
Comme la différence réside dans le terme - GML2/r3,
quand r
![]()
![]() les
comportements sont les mêmes dans les deux théories.
Mais quand r
les
comportements sont les mêmes dans les deux théories.
Mais quand r
![]() 0
le potentiel tend vers -
0
le potentiel tend vers -
![]() au
lieu de +
au
lieu de +
![]() dans
le cas Newtonien. A r = 2GM le potentiel vaut zéro.
En deçà de ce rayon c’est un trou noir, dont nous
parlerons plus loin. Pour les particules sans masse, il y a toujours
une barrière (sauf pour L =0 où le potentiel est
identiquement nul), mais un photon suffisamment énergétique
va néanmoins franchir cette barrière et être
aspiré vers le centre (Suffisamment énergétique
se rapporte au moment cinétique- en fait la fréquence
du photon est immatérielle, seule compte la direction dans
laquelle il pointe). Au sommet de la barrière les orbites
circulaires sont instables. Pour
dans
le cas Newtonien. A r = 2GM le potentiel vaut zéro.
En deçà de ce rayon c’est un trou noir, dont nous
parlerons plus loin. Pour les particules sans masse, il y a toujours
une barrière (sauf pour L =0 où le potentiel est
identiquement nul), mais un photon suffisamment énergétique
va néanmoins franchir cette barrière et être
aspiré vers le centre (Suffisamment énergétique
se rapporte au moment cinétique- en fait la fréquence
du photon est immatérielle, seule compte la direction dans
laquelle il pointe). Au sommet de la barrière les orbites
circulaires sont instables. Pour![]() = 0, g= 1, on peut facilement
résoudre (49) : on obtient :
= 0, g= 1, on peut facilement
résoudre (49) : on obtient :
|
|
(51) |
Ceci est représenté sur la figure qui
montre un maximum de V(r) à r = 3GM
pour chaque L. Cela veut dire qu’un photon peut orbiter
ad vitam eternam à ce rayon, mais que la moindre perturbation
l’éjecte soit à r = 0 soit à
r =
![]() .
.
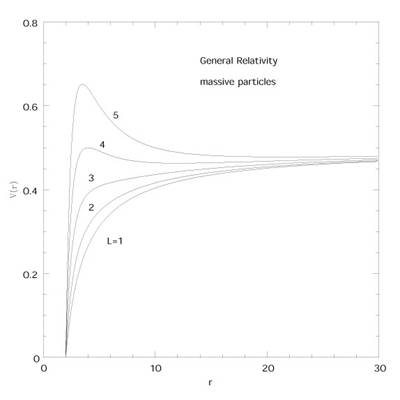
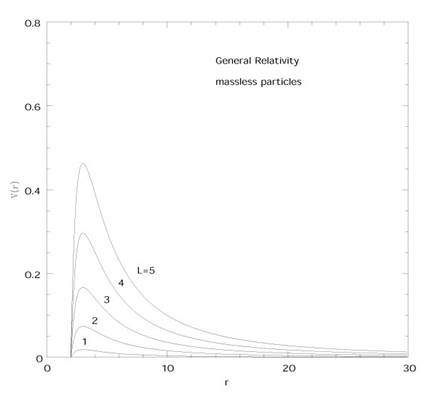
Pour les particules massives, il y a également différentes possibilités en fonction du moment cinétique. Les orbites circulaires sont :
|
|
(52) |
Pour les grandes valeurs de L, il y a deux orbites
circulaires, une stable et une instable, dans le cas où
L
![]()
![]() leurs
rayons sont :
leurs
rayons sont :
|
|
(53) |
Dans cette limite, l’orbite circulaire stable devient de plus en plus grande quand L croît, tandis que l’autre se rapproche de 3GM, situation qui rappelle le cas sans masse.
Quand L décroît les deux orbites circulaires se rapprochent, elles coïncident quand le discriminant de (52) s’annule pour :
|
|
(54) |
pour lequel :
|
|
(55) |
Il n’y a plus d’orbite circulaire stable sous cette valeur 6GM qui est le plus petit rayon possible pour une orbite stable dans la métrique de Schwarzschild.
Il y a aussi des orbites non captives, venant de l’infini et y retournant après avoir négocié un virage et des orbites captives mais non circulaires qui vont osciller autour du rayon de l’orbite circulaire stable. De telles orbites décrites exactement par des sections coniques en mécanique newtonienne auront des solutions différentes en Relativité générale, encore que nous allons avoir à résoudre l’équation dF/dt pour le démontrer.
Finalement, il y a des orbites venant de l’infini qui se terminent à r = 0. Ceci arrive si l’énergie est supérieure à la barrière ou pour L < Ö12 GM, quand la barrière disparaît totalement.
Nous avons donc trouvé que la solution de Schwarzschild comporte des orbites circulaires stables pour r > 6GM et des orbites circulaires instables pour 3GM < r < 6GM. Il est important de rappeler que tout ceci ne concerne que les géodésiques. Rien n’empêche d’arrêter une particule plongeant sous r = 3GM et la faire émerger aussi longtemps qu’elle reste au-delà de r = 2GM.
La plupart des expériences de Relativité générale concernent le mouvement des particules de test dans le système solaire et par-là même les géodésiques de la métrique de Schwarzschild, arrêtons-nous un instant sur ces tests.
Einstein proposa trois tests : La déviation des rayons lumineux, la précession du périhélie de Mercure et le décalage vers le rouge. La déviation des rayons lumineux est vérifiable dans le contexte de la limite du champ faible et n’est pas un bon exemple pour vérifier la forme exacte de la géométrie de Schwarzschild. Les observations effectuées pendant les éclipses ont confirmé la prédiction de la Relativité Générale (Encore qu’il y aurait à redire à certaines conditions expérimentales).
La précession du périhélie vient du fait que les orbites non circulaires ne sont pas des ellipses fermées, elles peuvent être approximativement décrites par des ellipses qui précèdent, décrivant un genre de motif floral.
En utilisant nos équations géodésiques,
nous pouvons les résoudre en dF/d![]() en termes d’une série de l’excentricité e
de l’orbite et de là obtenir la fréquence de
précession wa,
définie par 2
en termes d’une série de l’excentricité e
de l’orbite et de là obtenir la fréquence de
précession wa,
définie par 2![]() divisé par le temps mis à réaliser cette
précession d’un tour complet. Pour les détails
voir Weinberg comme d’habitude. La réponse est :
divisé par le temps mis à réaliser cette
précession d’un tour complet. Pour les détails
voir Weinberg comme d’habitude. La réponse est :
|
|
(56) |
Où nous avons réintroduit "c" pour faciliter la comparaison avec l’observation. (Vous pouvez à titre d’exercice établir cette relation au premier terme en e non nul). Historiquement la précession de Mercure à été le premier test de la Relativité Générale (Il faut dire que les données expérimentales existaient). Les données pour Mercure sont les suivantes :
|
|
(57) |
Et c = 3.00 × 1010 cm/sec. Ceci donne wa = 2.35 × 10-14 sec-1. Autrement dit, le grand axe de l’orbite de Mercure précède à un rythme de 42.9'' (42,9 secondes d’arc) par siècle. La valeur observée est 5601''/100 ans. De ceci il faut soustraire la précession des équinoxes de notre système de coordonnées géocentrique, soit 5025''/100 ans, pour être précis. Les perturbations gravitationnelles des autres planètes contribuent pour 532 ''/100 ans en sus, laissant les 43 ''/100 ans de contribution à la Relativité générale, conformes au calcul.
Le décalage vers le rouge est un autre effet qui est déjà sensible dans la limite du champ faible. Cet effet sera prédit par n’importe quelle théorie qui inclut le principe d’équivalence. Cependant comme il s’applique à des régions limitées de l’espace temps, son effet à grande échelle va dépendre de la métrique et donc de la théorie en question. Cela vaut donc la peine de le calculer dans la métrique de Schwarzschild. Considérons deux observateurs fixes aux coordonnées d’espace (r1,q1, F1) et (r2,q2,F2). Selon (45), le temps propre de l’observateur i va être relié à la coordonnée de temps t par :
|
|
(58) |
Supposons que l’observateur
![]() 1
émette une impulsion lumineuse qui voyage jusqu’à
l’observateur
1
émette une impulsion lumineuse qui voyage jusqu’à
l’observateur
![]() 2,
telle que
2,
telle que
![]() 1
mesure que l’intervalle entre deux crêtes consécutives
de l’onde lumineuse est
1
mesure que l’intervalle entre deux crêtes consécutives
de l’onde lumineuse est
![]() t1.
Chaque crête suit le même chemin vers
t1.
Chaque crête suit le même chemin vers![]() 2 séparée seulement par la coordonnée
de temps :
2 séparée seulement par la coordonnée
de temps :
|
|
(59) |
Cette séparation en coordonnée temps ne change pas le long de la trajectoire du photon, mais le deuxième observateur mesure un intervalle entre crêtes successives de :
|
|
(60) |
Comme ces intervalles
![]() t1
mesurent le temps propre entre deux crêtes d’une
onde électromagnétique, les fréquences observées
vont donc être :
t1
mesurent le temps propre entre deux crêtes d’une
onde électromagnétique, les fréquences observées
vont donc être :
|
|
(61) |
C’est un résultat exact pour le décalage de fréquence, dans la limite r >> 2GM nous avons :
|
|
(62) |
Ceci indique que la fréquence décroît
quand le potentiel
![]() croît,
ce qui se produit quand nous grimpons dans un champ gravitationnel,
d’où un décalage vers le rouge, ce qui est bien
conforme à ce que nous avions déduit du principe
d’équivalence.
croît,
ce qui se produit quand nous grimpons dans un champ gravitationnel,
d’où un décalage vers le rouge, ce qui est bien
conforme à ce que nous avions déduit du principe
d’équivalence.
[Note JF : Dans son livre « Space
time and Geometry » Sean M. Carroll a remplacé
cette démonstration par une démonstration plus
« physique » utilisant la conservation de
l’énergie d’un photon sur une géodésique
radiale. L’énergie (égale à la fréquence,
si on pose h =1) mesurée vaut :
ω = gμν Uµdxν/dλ,
relation qui définit en fait la normalisation de λ.
La 4-vitesse associée à l’observateur
statique de Schwarzschild vaut U0 =
(1-2GM/r)-1/2, ce qui donne U0
= (1-2GM/r)1/2 et donc : ω =
(1-2GM/r)1/2 dx0/dλ
= (1-2GM/r)1/2 dt/dλ = (1-2GM/r)-1/2
E, en utilisant la conservation de l’énergie E
donnée par (43). Dans ces conditions, avec les mêmes
conventions que ci-dessus on retrouve les équations (61) et
(62) mais établies de façon plus « physique ».]
Le pulsar binaire PSR 1913+16 découvert par Taylor en 1974 voit sa période orbitale décroître par émission de rayonnement gravitationnel. Cette décroissance minime, est conforme à la prédiction de théorie de la relativité générale avec une précision record de 10 -14
Un autre est le retard temporel gravitationnel avant une occultation, découvert et observé par Shapiro. C’est juste le fait que le temps écoulé sur deux géodésiques lumière différentes entre deux événements spatialement “identiques” mais à des moments différents où les conditions sur ces géodésiques sont différentes n’est pas forcément le même. Il a été mesuré par réflexion sur Vénus et Mars de signaux Radar avant occultation par le Soleil et est conforme à la prédiction de la RG.
Un autre effet qui n’a pas encore été observé directement est l’effet d’entraînement du référentiel de Lense-Thirring. Cependant, en 1997 une équipe américaine et une équipe italienne ont observé le phénomène d’entraînement du référentiel dans le voisinage d’étoiles à neutrons et de trous noirs, en étudiant l’énergie en rayons X émise lorsqu’ils absorbent de la matière. La quantité d’énergie émise et sa fréquence correspondent une précession de Lense-Thirring pour 3 des 15 étoiles à neutrons observées et pour les 5 trous noirs. Les scientifiques ont rappelé que ce ne sont pas des preuves définitives. La mesure directe de l’entraînement du référentiel par le champ terrestre (effet extrêmement faible) fait l’objet d’un projet, de lancement d’un satellite Gravity probe B qui utiliserait des gyroscopes d’extrême précision dont on mesurerait la précession en en extrayant la part due à la RG. A priori un tel projet n’est pas pour demain et peut être remis en cause à tout moment.
Nous connaissons maintenant le comportement des géodésiques à l’extérieur du rayon critique r = 2GM, ce qui concerne la situation dans notre système solaire et la plupart des objets astrophysiques.
Penchons- nous maintenant sur l’étude des objets dans le cadre de la métrique de Schwarzschild pour des valeurs de r inférieures à 2GM : les trous noirs. (Nous utiliserons le terme trou noir, même si nous n’avons pas encore bien défini ces objets).
Une façon de comprendre une géométrie
est d’explorer sa structure causale définie par ses
cônes de lumière. Nous allons considérer des
courbes radiales, donc
![]() et
f sont constants et ds2
= 0 :
et
f sont constants et ds2
= 0 :
|
|
(63) |
duquel on tire :
|
|
(64) |
Ceci mesure la pente des cônes de lumière,
sur un diagramme d’espace temps dans le plan t-r.
Si r est grand la pente vaut ±1, et ce sera
un espace Euclidien, quand nous approchons r = 2GM,
dt/dr
![]() ±
±![]() , et les cônes de lumière se ferment :
, et les cônes de lumière se ferment :
Ainsi, un rayon lumineux qui approche r = 2GM parait ne jamais l’atteindre du moins dans ce système de coordonnées, au lieu de cela, il semble s’en approcher asymptotiquement. Comme nous allons le voir, c’est une illusion, et le rayon de lumière (ainsi qu’une particule massive) n’a aucun problème à atteindre r = 2GM. Mais un observateur éloigné, ne s’en rendra pas compte. Si nous restions à l’extérieur, à bonne distance du trou noir, tandis qu’un observateur intrépide plongeait dans le trou noir, en nous envoyant des signaux régulièrement espacés dans son référentiel, nous recevrions ses signaux de plus en plus espacés :
Ceci apparaît clairement sur la figure et est
confirmé par le calcul de
![]() t1/
t1/![]() t2 que nous avons fait lorsque
nous nous intéressions au décalage spectral
gravitationnel (61).). Au fur et à mesure que l’astronaute
tombe vers r = 2GM, chaque intervalle fixe
t2 que nous avons fait lorsque
nous nous intéressions au décalage spectral
gravitationnel (61).). Au fur et à mesure que l’astronaute
tombe vers r = 2GM, chaque intervalle fixe
![]() t1
de son temps propre correspond à un temps de plus en
plus long
t1
de son temps propre correspond à un temps de plus en
plus long
![]() t2
de notre point de vue. Ceci continue à jamais, et
nous ne verrons jamais l’astronaute atteindre r = 2GM,
nous le verrons se déplacer de plus en plus lentement et
rougir à vue d’œil ce qui est bien normal quand on
est assez stupide pour se jeter dans un trou noir.
t2
de notre point de vue. Ceci continue à jamais, et
nous ne verrons jamais l’astronaute atteindre r = 2GM,
nous le verrons se déplacer de plus en plus lentement et
rougir à vue d’œil ce qui est bien normal quand on
est assez stupide pour se jeter dans un trou noir.
Le fait que nous ne le verrons jamais atteindre r = 2GM est une proposition sensée, mais le fait que sa trajectoire dans le plan t-r ne l’atteint pas, n’est pas fondée. Cette situation dépend de notre système de coordonnées et nous voudrions poser une question indépendante du système de coordonnées, telle que : l’astronaute atteint-il ce rayon critique en un temps fini de son temps propre ?
La meilleure façon est de changer de coordonnées pour un système qui n’est pas sujet à des bizarreries à r = 2GM. Puisque que nous avons montré la nature “référentielle” de la singularité, il y a des solutions pour la faire disparaître, et nous allons nous attacher à les trouver.
Il n’y a pas de moyen systématique pour trouver ces solutions, nous allons décrire notre démarche intuitive et l’appliquer. Nous allons procéder par étapes, en espérant faire les choix qui paraissent conformes aux objectifs que nous poursuivons.
Le problème avec notre système est
que dt/dr
![]()
![]() le
long des géodésiques radiales nulles quand nous
approchons r = 2GM, la progression dans la
direction de r devient de plus en plus lente selon la
coordonnée de temps t. On peut essayer de palier ce
problème en remplaçant t par une
coordonnée qui se meut elle aussi de plus en plus lentement le
long des géodésiques nulles.
le
long des géodésiques radiales nulles quand nous
approchons r = 2GM, la progression dans la
direction de r devient de plus en plus lente selon la
coordonnée de temps t. On peut essayer de palier ce
problème en remplaçant t par une
coordonnée qui se meut elle aussi de plus en plus lentement le
long des géodésiques nulles.
D’abord remarquons que l’on peut résoudre explicitement la condition (64) caractérisant les courbes nulles radiales pour obtenir :
|
|
(65) |
où la coordonnée de la tortue r* est définie par :
|
|
(66) |
La coordonnée de la tortue n’est valide que quand r ³ 2GM, car en deçà elle n’est pas définie (logarithme d’un nombre négatif). En termes de coordonnées de la tortue, la métrique de Schwarzschild devient :
|
|
(67) |
Où r est supposé une fonction de r*. Il y a un mieux, maintenant les cônes de lumière ne se referment plus, et de plus aucun des coefficients de la métrique n’explose pour r = 2GM (bien que gtt et gr*r* s’annulent). Le prix à payer pourtant est que la surface qui nous intéresse à r = 2GM a été rejetée à l’infini
Notre prochaine étape va être de définir des coordonnées naturellement adaptées aux géodésiques nulles. Si nous posons :
|
|
(68) |
Alors les géodésiques radiales nulles
entrantes sont caractérisées par
![]() =
constante, tandis que celles sortantes satisfont
=
constante, tandis que celles sortantes satisfont
![]() =
constante (cf 65). Revenons à la coordonnée
initiale r, mais remplaçons la coordonnées de
temps t par la nouvelle coordonnée
=
constante (cf 65). Revenons à la coordonnée
initiale r, mais remplaçons la coordonnées de
temps t par la nouvelle coordonnée
![]() .
.
Nous définissons ainsi les coordonnées de Eddington-Finkelstein. En ces termes la métrique est :
|
|
(69) |
Nous voyons là un réel signe de
progrès. Même si le coefficient de la métrique
g![]()
![]() s’annule
pour r = 2GM, il n’y a pas dégénérescence,
le déterminant de la métrique vaut :
s’annule
pour r = 2GM, il n’y a pas dégénérescence,
le déterminant de la métrique vaut :
|
|
(70) |
Ce qui est tout ce qu’il y a de plus régulier
à r = 2GM. Donc la métrique est
inversible et nous voyons une fois pour toutes que r = 2GM
est simplement une singularité de coordonnées de notre
système original (t, r,![]() ,f) En coordonnées
Eddington-Finkelstein la condition de courbe radiale nulle
s’exprime :
,f) En coordonnées
Eddington-Finkelstein la condition de courbe radiale nulle
s’exprime :
|
|
(71) |
Nous voyons que la transformation préserve un cône de lumière régulier à r = 2GM, et que la coordonnée de cette surface est à une distance finie. Il n’y a pas non plus de problème pour les chemins de type lumière ou temps au-delà de la surface. Poursuivons notre démarche.
Certes les cônes de lumière ne se ferment pas, mais ils s’inclinent progressivement ce qui fait que pour r < 2GM tous les chemins pointant vers le futur correspondent à r décroissant.
La surface r = 2GM, tout en étant régulière localement se comporte comme un point de non-retour, une particule qui passe ce point ne reviendra jamais. Pour cela r = 2GM est appelé l’horizon, événementiel, aucun événement à r £ 2GM ne peut influencer un autre événement à r > 2GM.
Remarquons que l’horizon, événementiel est une surface de type nul, pas de type temps. Remarquons également que comme rien ne peut s’en échapper par cet horizon, il est impossible de voir à l’intérieur d’où le nom de trou noir.
Revenons sur ce que nous avons fait. Du fait que
notre système de coordonnées original n’était
pas approprié à la description de notre variété
en son entier, nous avons changé la cordonnée t en
une nouvelle
![]() ,
dont la qualité essentielle est de ne pas présenter
de singularité lorsque nous faisons décroître r
le long d’une courbe de type lumière
,
dont la qualité essentielle est de ne pas présenter
de singularité lorsque nous faisons décroître r
le long d’une courbe de type lumière
![]() =
constante, nous permettant d’atteindre l’horizon sans
souci. Un observateur local traverserait l’horizon sans
s’en apercevoir, la géométrie n’étant
pas différente d’ailleurs.
=
constante, nous permettant d’atteindre l’horizon sans
souci. Un observateur local traverserait l’horizon sans
s’en apercevoir, la géométrie n’étant
pas différente d’ailleurs.
Nous concluons que nos soupçons étaient fondés et que le système de coordonnées initial n’était pas approprié pour décrire au mieux la variété en son entier. La région r £ 2GM doit appartenir à notre espace temps puisque des particules physiques peuvent y accéder normalement.
Rien ne prouve que nous en avons terminé, il y a peut être d’autres directions vers lesquelles nous pouvons étendre notre variété.
En fait, il y en a. Remarquons que dans le système
de coordonnées (![]() , r) nous pouvons traverser l’horizon événementiel
dans le sens du futur, mais pas dans celui du passé.
, r) nous pouvons traverser l’horizon événementiel
dans le sens du futur, mais pas dans celui du passé.
Ceci semble déraisonnable, puisque nous
sommes partis d’une solution indépendante du temps. Si
on avait choisi
![]() à
la place de
à
la place de
![]() ,
dans ce cas la métrique aurait été :
,
dans ce cas la métrique aurait été :
|
|
(72) |
On pourrait toujours traverser l’horizon, mais dans le sens du passé cette fois : on ne peut que ressortir.
C’est quand même surprenant, nous
pouvons soit avoir des chemins dirigés vers le futur, soit
vers le passé pour traverser l’horizon r = 2GM,
mais nous arrivons à différents endroits. On pouvait
s’en douter du fait de la définition de (68) puisque
![]() constant
et r décroissant, t
constant
et r décroissant, t
![]() +
+
![]() ,
tandis que à
,
tandis que à
![]() constant
r décroissant t
constant
r décroissant t
![]() -
-
![]() .
Les coordonnées de la tortue r* tendent vers
-
.
Les coordonnées de la tortue r* tendent vers
-
![]() quand
r
quand
r
![]() 2GM.
Donc nous avons étendu l’espace temps dans deux
directions différentes, une vers le passé, une vers le
futur.
2GM.
Donc nous avons étendu l’espace temps dans deux
directions différentes, une vers le passé, une vers le
futur.
Poursuivons, maintenant en examinant si en suivant
des géodésiques de type espace, nous allons couvrir
d’autres régions. Effectivement cela permet explorer
d’autres régions de l’espace temps. Pour gagner du
temps allons droit au but et définissons des coordonnées
satisfaisantes partout. La première idée qui vient à
l’esprit est d’utiliser
![]()
![]() à
la place de t et r. Cela conduit à :
à
la place de t et r. Cela conduit à :
|
|
(73) |
Avec r défini implicitement en termes
de
![]() et
et
![]() par :
par :
|
|
(74) |
Ce faisant nous avons réintroduit la
dégénérescence de départ, dans ces
coordonnées r = 2GM est rejeté à
l’infini (soit à
![]() =
-
=
-
![]() soit
à
soit
à
![]() =
+
=
+
![]() ).
Changeons donc ces coordonnées de façon à
ramener ces points à distance finie. Un bon choix est :
).
Changeons donc ces coordonnées de façon à
ramener ces points à distance finie. Un bon choix est :
|
|
(75) |
Par rapport aux coordonnées initiales (t, r) cela donne :
|
|
(76) |
Dans le système de coordonnées (u’,
v',![]() ,F) la métrique de Schwarzschild
est :
,F) la métrique de Schwarzschild
est :
|
|
(77) |
Ainsi toute forme de singularité de la métrique à r = 2GM disparaît complètement, les coefficients restant bien sages à l’horizon événementiel.
Les coordonnées u’ et v'
sont toutes deux de type " nul ", car leur dérivées
partielles
![]() /
/![]() u’ et
u’ et
![]() /
/![]() v' sont des vecteurs nuls. Cela ne gène en rien
du fait que les quatre vecteurs dérivées
partielles (deux nuls et deux de type espace) de ce système
peuvent servir valablement de base à l’espace tangent.
v' sont des vecteurs nuls. Cela ne gène en rien
du fait que les quatre vecteurs dérivées
partielles (deux nuls et deux de type espace) de ce système
peuvent servir valablement de base à l’espace tangent.
Néanmoins il est plus aisé de travailler dans un système dont une coordonnée est de type temps et les autres de type espace. Nous définissons donc :
|
|
(78) |
et
|
|
(79) |
En ces termes la métrique devient :
|
|
(80) |
où r est implicitement défini par :
|
|
(81) |
Les coordonnées (v, u,![]() ,F) sont dénommées
coordonnées de Kruskal ou quelquefois coordonnées
de Kruskal-Szekeres. Notons que v est la coordonnée de
type temps.
,F) sont dénommées
coordonnées de Kruskal ou quelquefois coordonnées
de Kruskal-Szekeres. Notons que v est la coordonnée de
type temps.
L’intervalle de variation de u, v peut, être étendue comme suit : - ¥ < u, v < + ¥ avec v² < u² +1, sur la base de l’équation (81). Ce qui permet de couvrir les quatres régions délimitées par le diagramme de Kruskal. La relation " v² < u² + 1 " vient du fait que la valeur minimum de (81), qui est obtenue lorsque r = 0, vaut " -1".
Pour obtenir les valeurs de t, r à partir de u, v et réciproquement, à partir des équations (78) et (79) on voit qu’il faut généraliser leur expression en les écrivant :
u = +/- ç (r/2GM) - 1ç1/2 e r/4GM . cosh (t/4GM) (78 ')
v = +/- ç (r/2GM) - 1ç1/2 e r/4GM . sinh (t/4GM) (79 ')
La valeur entre " ç" signifiant " valeur absolue" (sinon on pourrait prendre la racine carrée d’un nombre négatif) les signes "+ et -" étant une conséquence de (81) si u, v sont solutions de (81) alors -u et -v le sont également. Ceci s’applique rétroactivement à certaines expressions intermédiaires.
Il faut quand même remarquer que malgré cette généralisation (78') et (79') "t" n’est pas défini quand r < 2GM (Zones II et III du diagramme qui suit).
Les coordonnées de Kruskal possèdent certaines propriétés “miraculeuses”. A l’instar des coordonnées (t, r*) les courbes nulles radiales (cf 80) ont la même forme que dans un espace Euclidien.
|
|
(82) |
À la différence des coordonnées (t, r*) pourtant, l’horizon événementiel, r = 2GM n’est pas à l’infini, il est défini par (cf 81) :
|
|
(83) |
Compatible avec son état de surface nulle. Plus généralement, si on considère les surfaces r = constant, de (81) elles satisfont :
|
|
(84) |
Ce qui correspond à une hyperbole dans le plan u- v. De plus les surfaces à t = constante sont données par :
|
|
(85) |
Ce qui correspond à des droites passant par
l’origine et de pente tanh (t/4GM). Remarquons
que quand t
![]() ±
±![]() (tanh ±
(tanh ±![]()
![]() 1)
ceci converge vers la valeur définie dans (83) donc ces
surfaces sont les mêmes que pour r = 2GM et
remarquons que t n’est pas défini pour une
pente supérieure à 1, (Zones II et III du
diagramme qui suit) puisque v/u = tanh
t/4GM £
1.
1)
ceci converge vers la valeur définie dans (83) donc ces
surfaces sont les mêmes que pour r = 2GM et
remarquons que t n’est pas défini pour une
pente supérieure à 1, (Zones II et III du
diagramme qui suit) puisque v/u = tanh
t/4GM £
1.
Maintenant nos coordonnées (v,
u) peuvent prendre n’importe quelles valeurs sans se
heurter à la singularité à r =
2GM. La région autorisée est donc -
![]() £
u £
£
u £
![]() et
v2 < u2
+ 1. Nous pouvons tracer un diagramme de l’espace temps
dans le plan u, v (sans s’intéresser à q,
F, ce qui compte tenu de la symétrie
sphérique n’enlève rien à l’intérêt
de la discussion), appelé le diagramme de Kruskal, qui
représente l’espace temps entier correspondant à
la métrique de Schwarzschild.
et
v2 < u2
+ 1. Nous pouvons tracer un diagramme de l’espace temps
dans le plan u, v (sans s’intéresser à q,
F, ce qui compte tenu de la symétrie
sphérique n’enlève rien à l’intérêt
de la discussion), appelé le diagramme de Kruskal, qui
représente l’espace temps entier correspondant à
la métrique de Schwarzschild.

Chaque point du diagramme est une sphère S².
Nos coordonnées originales (t, r) étaient uniquement pertinentes pour r > 2GM, ce qui ne représente qu’une partie de la variété représentée par le diagramme de Kruskal, mais nous avons fait les extensions nécessaires (78' et 79').
Il est pratique de diviser le diagramme en quatre régions.
La métrique de Schwarzschild n’est valide que dans la région I. Nous sommes donc partis de la région I, en suivant des rayons “nuls” pointés vers le futur et grâce à la première transformation de coordonnées (Eddington-Finkelstein), nous avons pu franchir la barrière à r = 2GM et nous avons atteint la région II, puis, avec les mêmes coordonnées, en suivant les rayons pointés vers le passé nous avons atteint la région III. Nous avons, de nouveau, changé de coordonnées (Kruskal) pour étendre encore notre exploration sur les géodésiques de type espace et cela nous a conduit à la région IV.
Les définitions (78) et (79) qui relient (u, v) à (t, r) ne sont valables que dans la région I. Dans les autres régions il est nécessaire d’introduire des “valeurs absolues” et des signes “plus” ou “moins” de façon appropriée pour que les coordonnées ne deviennent pas imaginaires (malgré cela "t" n’est pas défini dans les zones II et III).
Ayant étendu la géométrie de Schwarzschild aussi loin que possible, nous avons décrit un espace temps remarquable.
La Région II, bien sûr que nous identifions à un trou noir. Quand quelque chose voyage de la région I vers II, il ne revient jamais. En fait tout chemin pointé vers le futur en région deux se termine inexorablement à la singularité r = 0.
Cela vaut la peine d’insister, non seulement, on ne peut pas s’échapper pour retourner à la région I, mais on ne peut même pas s’arrêter de se rapprocher de r = 0, car la coordonnée r décroissante correspond à la flèche du temps. (Ceci était déjà évident dans notre système de coordonnées initial, car pour r < 2GM, t devient de type espace et r devient de type temps).
Alors vous ne pouvez pas plus arrêter votre voyage fatal vers la singularité que d’arrêter de vieillir.
Pire, comme le temps est maximum le long de la géodésique, si vous tentez de lutter contre cette aspiration, vous ne faites que précipiter votre fin (effet sables mouvants).
Le mieux est d’envisager la situation avec sérénité, d’autant que l’issue finale est très proche. Les forces de marée qui deviennent infinies à l’approche de la singularité auront tôt fait de vous réduire en pièces. Si vous êtes amateur de sensations fortes, tous les détails, dans Misner, Thorne, et Wheeler, section 32.6. Bien qu’ils utilisent des repères orthonormés, cela ne rend pas le voyage plus attrayant.
Les régions III et IV étaient plutôt inattendues.
La région III est similaire à la région II, mais où on remonterait le temps, une partie de l’espace temps dont les objets peuvent s’échapper mais ne peuvent pas y pénétrer.
On peut voir cela comme une fontaine blanche. Il y a une singularité dans le passé et une partie de l’univers semble sortir “ex nihilo” de l’horizon de la région III vers la région IV. Cet horizon est quelquefois appelée l’horizon événementiel du passé alors que celui de la région II est appelée l’horizon événementiel du futur.
La région IV, ne peut pas être atteinte depuis notre région I soit du passé soit vers le futur. Réciproquement un observateur logeant à cet endroit ne peut pas nous atteindre. C’est une autre région asymptotiquement plate de l’espace temps, comme une image dans un miroir de la nôtre.
On va voir qu’elle est cependant connectée à la région I par un trou de ver, un goulot d’étranglement spatio-temporel reliant deux régions distinctes. Examinons le diagramme de Kruskal en le découpant en surfaces de type espace à v constant :
Dessinons chaque tranche en restaurant une des coordonnées angulaires pour clarifier.
Le diagramme ci-dessus est spatio-temporel.
Chaque cercle horizontal de rayon "r" (cf hyperboles à r = constante) est en fait une sphère, l’axe des "u" est vertical,
Donc la géométrie de Schwarzschild décrit vraiment deux régions asymptotiquement plates qui mènent l’une vers l’autre, se connectent via un trou de ver pendant très un court instant puis se déconnectent. Mais les trous de vers se ferment trop rapidement pour qu’un observateur puisse passer d’une région à l’autre.
Cette histoire de deux espaces temps miroirs, séparés communiquant pendant un court instant puis se refermant parait assez invraisemblable. Il n’est pas sûr que cela se passe vraiment ainsi dans le monde physique, car la métrique de Schwarzschild ne modélise pas avec précision l’univers entier. N’oublions pas qu’elle n’est valide que dans le vide, à l’extérieur des étoiles par exemple. Si cette étoile a un rayon supérieur à 2GM, nous n’aurons pas à nous soucier d’horizons événementiels.
Mais nous pensons que des étoiles qui s’effondrent sous l’action de leur propre contraction gravitationnelle jusqu’à un rayon inférieur à r = 2GM peuvent finir en singularité et produire un trou noir. On ne connaît pas de cause physique aux fontaines blanches, et on n’en a pas observé à ce jour, mais comme le passé d’un tel espace temps est conforme à la solution complète de Schwarzschild, rien ne s’y oppose en théorie.
Grosso modo un diagramme de Kruskal pour un effondrement d’étoile va ressembler à :
La région ombrée n’est pas décrite par Schwarzschild, donc il n’y a pas de place pour les fontaines blanches et trous de ver associés.
Pendant que nous y sommes disons un mot de la formation des trous noirs astrophysiques par effondrement d’étoiles massives. La vie d’une étoile résulte d’un équilibre entre la pression générée par les réactions nucléaires en son noyau et sa contraction liée à la gravitation. Tant que l’étoile dispose d’assez d’hydrogène, il y a rayon qui correspond à une situation stable. En fin de vie, malgré d’autres réactions, lorsque le combustible nucléaire s’épuise, la pression n’arrive plus à compenser l’action de la gravitation et l’étoile commence à s’effondrer, ceci peut être accompagné d’éjection violente d’une grande quantité de matière (nova, supernova), mais si la matière restante est suffisante le processus continue. Le phénomène peut être stoppé par le phénomène quantique d’exclusion de Pauli (auquel cas on obtient une naine blanche). Si la masse est suffisamment importante la pression de dégénérescence ne suffit pas et les électrons se combinent avec les protons en neutrons, en une transition de phase très énergétique. La densité d’une telle étoile est de 1015 g/cm3, très proche de la densité critique1016 g/cm3 de formation des trous noirs. La pression du gaz dégénéré de neutrons peut stopper la contraction et on peut obtenir une étoile à neutrons qui serait pratiquement entièrement constitué de neutrons (L’intérieur des étoiles à neutrons n’est pas très bien connu). Les conditions au centre d’une étoile à neutrons, sont très différentes de ce que nous observons sur terre, aussi nous ne connaissons pas bien l’équation d’état associée. Cependant nous pensons, qu’une étoile à neutron suffisamment massive, ne devrait pas pouvoir résister à l’effondrement gravitationnel. Comme un fluide de neutrons, est le matériau le plus dense que nous connaissions, on peut raisonnablement penser que le résultat de son effondrement doit générer un trou noir.
Le processus est résumé sur le diagramme ci-dessous : rayon en fonction de la masse.
Ce diagramme montre que pour une masse donnée M, le rayon va décroître en suivant la courbe jusqu’au point d’équilibre. Les naines blanches se trouvent entre A et B, les étoiles à neutrons entre C et D. Le point B est à une ordonnée de 1,4 Masses solaires, le point D bien que moins certain, probablement un peu en dessous de 2 masses solaires.
Le processus d’effondrement n’est pas simple (la masse pouvant varier fortement en cours de ce processus) comme indiqué précédemment, aussi le point final d’évolution d’une étoile est difficile à prédire.
Mais, les naines blanches sont monnaie courante, les étoiles à neutrons ne sont pas rares et nous avons repéré certains systèmes où il y a de fortes présomptions de présence de trous noirs.
Bien sûr nous ne pouvons pas les voir directement. Mais on peut détecter le rayonnement résultant de l’accrétion de matière dans le trou, qui la chauffe et la fait rayonner. On peut aussi détecter ses effets gravitationnels.
Nous avons vu que le système de coordonnées de Kruskal nous offre une représentation très utile de la géométrie de Schwarzschild
Avant de nous intéresser à d’autres types de trous noirs, introduisons une nouvelle manière de penser l’espace temps, Le diagramme de Penrose (où de Carter-Penrose, où diagramme conforme).
L’idée consiste à opérer une transformation conforme qui ramène la variété entière, qui peut être infinie, à une figure géométrique finie, de telle sorte que nous puissions la représenter sur une simple feuille de papier, ceci facilitant, au prix d’une petite gymnastique intellectuelle, la discussion des solutions d’espace temps obtenues.
Faisons-nous la main sur l’espace de Minkowski pour voir comment ça marche. La métrique en coordonnées polaires est :
|
|
(86) |
Les coordonnées
![]() ,F
ne posent pas de problème de représentation, mais les
deux autres sortent manifestement de la feuille de papier.
,F
ne posent pas de problème de représentation, mais les
deux autres sortent manifestement de la feuille de papier.
|
|
(87) |
La ligne d’univers r = 0 qui représente une singularité de coordonnées devrait être couverte spécifiquement, mais comme nous connaissons ce qui s’y passe, nous allons faire comme si tout était normal à r = 0.
Simplifions-nous la vie en utilisant les coordonnées nulles.
|
|
(88) |
Dont l’intervalle de variation est :
|
|
(89) |
Cette portée est représentée sur la figure, dans laquelle chaque point représente une sphère S² de rayon r = u - v. La métrique dans ces coordonnées, est donnée par :
|
|
(90) |
Nous voulons maintenant opérer un changement de coordonnées qui ramène l’infini à une distance finie. Un bon choix est :
|
|
(91) |
L’intervalle est maintenant :
|
|
(92) |
Pour obtenir la métrique nous utiliserons :
|
|
(93) |
et
|
|
(94) |
et de même pour v. Nous sommes conduits à :
|
|
(95) |
Tandis que :
|
|
(96) |
Donc la métrique de Minkowski dans ces coordonnées, est :
|
|
(97) |
L’expression est sympathique, la métrique apparaissant comme une expression assez simple multiplié par un facteur global.
On peut améliorer en réintroduisant une coordonnée temporelle het une coordonnée spatiale c via :
|
|
(98) |
avec un intervalle :
|
|
(99) |
Maintenant la métrique est :
|
|
(100) |
où :
|
|
(101) |
La métrique de Minkowski peut donc être représentée par la métrique “non physique” résultant d’une transformation conforme.
|
|
(102) |
Elle correspond à une variété
![]() ×
S3, où l’hypersphère
S3 est à symétrie maximale et est statique.
Cette métrique est courbée et elle n’est pas une
solution aux équations d’Einstein dans le vide. Ne nous
formalisons pas, cette métrique n’est pas physique. La
vraie métrique obtenue par la transformation conforme inverse
est la métrique d’un espace plat. En fait cette métrique
est celle de l’univers statique (mais instable)
d’Einstein, solution de ses équations pour un fluide
parfait et une constante cosmologique. L’intervalle complet des
coordonnées sur
×
S3, où l’hypersphère
S3 est à symétrie maximale et est statique.
Cette métrique est courbée et elle n’est pas une
solution aux équations d’Einstein dans le vide. Ne nous
formalisons pas, cette métrique n’est pas physique. La
vraie métrique obtenue par la transformation conforme inverse
est la métrique d’un espace plat. En fait cette métrique
est celle de l’univers statique (mais instable)
d’Einstein, solution de ses équations pour un fluide
parfait et une constante cosmologique. L’intervalle complet des
coordonnées sur
![]() ×
S3 est :
×
S3 est :
![]() <
h< +
<
h< +
![]() ,
0 £ c £
p.
,
0 £ c £
p.
![]() ×
S3 dans son entier est donc représenté
par un cylindre, dans lequel chaque cercle est une hypersphère
comme montré ci après. L’espace de Minkowski est
plus restreint, car limité au sous espace défini par
(99).
×
S3 dans son entier est donc représenté
par un cylindre, dans lequel chaque cercle est une hypersphère
comme montré ci après. L’espace de Minkowski est
plus restreint, car limité au sous espace défini par
(99).
Les régions ombrées représentent l’espace de Minkowski Remarquons que chaque point (h, c) sur ce cylindre est la moitié d’une sphère S² alors que l’autre moitié correspond au point (h, -c).
Si on déroule la région ombrée on peut représenter l’espace de Minkowski comme un triangle, comme la figure ci après le montre :
C’est le diagramme de Penrose. Chaque point représente une sphère S². En fait l’espace temps de Minkowski est seulement l’intérieur du diagramme ci-dessus incluant c = 0. Les limites n’en font pas partie. Ensemble elles sont référencées comme infinité conforme. La structure du diagramme de Penrose nous permet de subdiviser l’infinité conforme en différentes régions :
Notons que :
i + : infini temporel du futur (h=p, c = 0),
i0 : infini spatial (h = 0, c = p) et,
i - : infini temporel du passé ( h = - p, c = 0) sont vraiment des points, car c = 0 et c = π sont les pôles Nord et Sud de l’hypersphère S3.
Tandis que :
I + :(h = p - c où 0 < c < p) : surface nulle de l’infini du futur et,
I - :(h = - p + c où 0 < c < p): surface nulle de l’infini du passé, sont vraiment des surfaces nulles avec la topologie R×S2.
Le diagramme de Penrose rassemble un nombre important de caractéristiques pour l’espace temps de Minkowski.
On peut imaginer que les points i+, et i- sont les limites de surfaces spatiales dont les normales sont temporelles, et vice versa pour i0. Toutes les géodésiques radiales nulles sont à ±45° dans le diagramme. Toutes les géodésiques temporelles commencent à i- et finissent à i+, toutes les géodésiques nulles commencent à I - et finissent à I +, toutes les géodésiques spatiales commencent et finissent à i0. Par ailleurs, il peut y avoir des courbes de type temps non géodésiques qui se terminent à l’infinité nulle (si elles deviennent “asymptotiquement” nulles).
Il est agréable de représenter tout l’espace de Minkowski sur une feuille de papier, mais cela ne nous apprend rien que nous ne sachions déjà. Le diagramme de Penrose est plus utile quand nous voulons représenter des espaces temps plus complexes, tels que ceux relatifs aux trous noirs. L’utilisation première du diagramme de Penrose a été la comparaison d’espaces temps à l’infini avec l’espace temps de Minkowski. La définition rigoureuse de "asymptotiquement plat " est " possédant une infinité conforme identique à celle de l’espace temps de Minkowski."
Nous ne rentrerons pas plus dans les détails, car nous allons plutôt nous intéresser à l’analyse des trous noirs à l’aide du diagramme de Penrose.
Nous éluderons certaines opérations intermédiaires, car le parallèle avec la métrique de Minkowski est d’une grande complexité algébrique. Partons de la version des coordonnées nulles de Kruskal (77) dans laquelle la métrique prend la forme :
|
|
(103) |
où r est défini implicitement via :
|
|
(104) |
Alors la même transformation de coordonnées que celle utilisée pour l’espace plat suffisent à ramener l’infini à distance raisonnable.
|
|
(105) |
Dans les intervalles :
|
|
La partie de la métrique dépendant de (u", v") (qui est à coordonnées angulaires constantes) est maintenant en relation conforme avec l’espace de Minkowski. Dans ces nouvelles coordonnées les singularités à r = 0 sont des lignes droites qui s’étendent de l’infini temporel dans une région asymptotique à l’infini temporel dans l’autre. Le diagramme de Penrose pour la solution de Schwarzschild la plus complète a cette allure :
La seule difficulté de compréhension de ce diagramme est que i+ et i- n’appartiennent pas à r = 0 (Il y a de nombreux chemins de type temps qui ne rencontrent pas la singularité). Remarquons aussi la structure de l’infini conforme identique à celui de l’espace de Minkowski, cohérent avec la nature asymptotiquement plate de la métrique de Schwarzschild.
Le diagramme de Penrose relatif à l’effondrement d’une étoile en trou noir est bien conforme à ce que l’on peut escompter comme montré ci après.
Là encore, le diagramme de Penrose ne nous apprend rien de neuf, son intérêt va apparaître lorsque nous allons considérer des trous noirs plus généraux.
Il devrait y avoir en principe une grande diversité de trous noirs, dépendant de leur processus de formation. Il n’en est rien, nonobstant ses origines, il évolue (rapidement) vers un état caractérisé uniquement par sa masse, sa charge et son moment cinétique. Cette propriété qui doit être démontrée pour les diverses configurations de champ qui conduisent à la formation d’un trou noir a conduit les physiciens à déclarer dans un élan poétique que “les trous noirs n’ont pas de poils”. On peut montrer par exemple qu’un trou qui se forme à partir d’un effondrement inhomogène, se débarrasse des inhomogénéités en émettant un rayonnement gravitationnel. C’est un exemple du théorème " pas de poils".
Nous allons nous intéresser à la forme que prend un trou noir (supposé déjà existant), dans le cas des trous chargés et en rotation. Il existe de solutions exactes dans les deux cas et nous allons les examiner.
Au passage faisons un petit crochet par
l’évaporation des trous noirs. Cela parait plutôt
étrange qu un trou noir puisse s’évaporer, mais
en notre monde imparfait les trous noirs ne sont pas complètement
noirs, ils rayonnent de l’énergie comme s’ils
étaient un corps noir à une température de T
=
![]() /8
/8![]() kGM, où M est la masse du trou et k
la constante de Boltzmann.
kGM, où M est la masse du trou et k
la constante de Boltzmann.
Cet effet qui est appelé rayonnement de Hawking, s’appuie sur la théorie du champ quantifié dans les espaces courbes est en dehors de notre champ d’investigation actuel.
L’idée de base est par contre tout à fait compréhensible.
|
|
En théorie des champs quantique, on doit tenir compte des “fluctuations du vide”, matérialisés par les créations / annihilations de particules / antiparticules virtuelles dans le vide. Ces fluctuations sont semblables aux oscillations autour de zéro d’un oscillateur harmonique. Dans des conditions normales, ces fluctuations sont indétectables leur moyenne correspondant à une énergie nulle (ce que personne ne comprend, c’est le problème de la constante cosmologique). En présence de l’horizon d’un trou noir pourtant, il se peut qu’un des membres de la paire tombe et soit piégé dans le trou noir, alors que l’autre s’échappe vers l’infini. La particule qui va vers l’infini aura une énergie positive et comme l’énergie doit être conservée, le trou doit perdre de l’énergie donc de la masse. On peut aussi dire que la particule capturée par le trou noir a une masse négative. Les particules s’échappant de l’horizon constituent le rayonnement d’Hawking. Ce n’est pas un effet très important, et comme la température baisse quand la masse croît, pour des trous noirs de masses voisines de celles du soleil, il est complètement négligeable. N’empêche qu’en principe, le trou noir peut perdre toute sa masse et se réduire à néant dans le processus. Le diagramme de Penrose correspondant devrait ressembler à :
Il pourrait tout autant ne pas y ressembler. Le problème avec ce diagramme est que de l’information est perdue. Si nous traçons une surface de type espace dans le passé de la singularité et la faisons évoluer vers le futur, une partie vient s’écraser sur la singularité et est détruite. Ce qui fait que le rayonnement lui- même contient moins d’information qu’il n’y en avait à l’origine dans l’espace temps.
C’est pire que le manque de poils sur le trou noir En effet s’il est contrariant de penser que l’information a pu être piégée dans le trou noir derrière l’horizon événementiel, il est désolant de penser qu’elle a pu disparaître corps et biens. Un tel processus viole la conservation de l’information, qui est implicite en relativité générale et en mécanique quantique. Ce paradoxe est pris très au sérieux, et de nombreux travaux s’efforcent de comprendre comment l’information pourrait être retrouvée. Une explication en vogue s’appuie sur la théorie des cordes, qui stipule que les trous noirs ont en fait des tas de poils sous la forme d’états de cordes virtuelles nichant près de l’horizon événementiel. Nous arrêterons là nos investigations, tout en nous rappelant l’intense activité que ces problèmes suscitent.
Ceci étant dit tournons-nous maintenant vers les trous noirs chargés. Il parait raisonnable de considérer de tels objets, puisque nous avons admis l’existence de trous noirs, et que rien ne nous empêche de les supposer chargés électriquement. En astrophysique pourtant, on rencontre rarement des charges importantes (l’univers est supposé globalement électriquement neutre), donc nous la supposerons très faible par rapport à la masse en termes d’effets des champs générés. Toutefois les trous noirs chargés nous offrent des possibilités intéressantes d’expériences de pensée, donc nous allons nous y intéresser.
La symétrie sphérique s’applique toujours, nous savons que nous pouvons écrire la métrique :
|
|
(106) |
Mais nous ne sommes plus dans le vide, car le trou a un champ électromagnétique non nul, qui est une source d’énergie et d’impulsion.
Le tenseur énergie-impulsion s’écrit :
|
|
(107) |
où Fmn est le tenseur d’intensité du champ électromagnétique. En symétrie sphérique le tenseur intensité du champ le plus général va avoir les composantes suivantes :
|
|
(108) |
où f (r, t) et g(r,
t) sont des fonctions à déterminer par les
équations du champ et où les composantes non écrites
sont réputées nulles. Ftr correspond
au champ électrique radial tandis que F![]() F correspond
au champ magnétique radial. (Pour ceux qui s’étonnent
de la présence de sin
F correspond
au champ magnétique radial. (Pour ceux qui s’étonnent
de la présence de sin![]() , je rappelle que ce qui doit être indépendant de
, je rappelle que ce qui doit être indépendant de
![]() et
de F c’est la composante radiale du
champ magnétique, Br =e01mnFmn.
En symétrie sphérique ersmn
=
et
de F c’est la composante radiale du
champ magnétique, Br =e01mnFmn.
En symétrie sphérique ersmn
=
![]()
![]() est
proportionnel à (sin
est
proportionnel à (sin![]() )-1,
donc nous nécessitons un facteur sin
)-1,
donc nous nécessitons un facteur sin![]() dans F(
dans F(![]() F). Les équations
du champ dans ce cas sont les équations d’Einstein et
celles de Maxwell :
F). Les équations
du champ dans ce cas sont les équations d’Einstein et
celles de Maxwell :
|
|
(109) |
Les deux jeux d’équations sont couplés puisque le tenseur électromagnétique intervient en tant que tenseur énergie Impulsion de l’équation d’Einstein tandis que la métrique intervient dans l’équation de Maxwell. Les difficultés ne sont pas insurmontables et la même méthode que celle utilisée avec succès pour les équations du vide conduit à la solution pour le cas chargé. Pour faire court nous allons sauter directement au résultat final.
La solution est connue sous le nom de métrique de Reissner-Nordstrøm et est donnée par :
|
|
(110) |
où
|
|
(111) |
M est la masse du trou noir, q est la charge électrique totale et p est la charge magnétique totale.. Les charges magnétiques isolées (monopoles) n’ont jamais été observées, mais cela ne nous gênera pas d’écrire la métrique qu’elles généreraient si elles existaient. Nous avons de bonnes raisons de penser que les monopoles existent, mais qu’ils sont extrêmement rares. (De toutes façons, un trou noir peut avoir une charge magnétique même sans monopoles). En fait les charges électriques et magnétiques interviennent dans la métrique de la même façon, donc cela ne complique rien de garder p dans nos expressions. Les champs électromagnétiques associés à ces solutions sont donnés par :
|
|
(112) |
Mais, les irréductibles peuvent poser p = 0.
La structure des singularités et des horizons
événementiels est plus complexe dans cette métrique
que dans celle de Schwarzschild, du fait du terme supplémentaire
dans la fonction
![]() (r)
(qui peut être interprétée comme mesurant
l’inclinaison du cône de lumière).
(r)
(qui peut être interprétée comme mesurant
l’inclinaison du cône de lumière).
Ce qui reste identique c’est qu’à r = 0, il y a une vraie singularité de courbure comme on peut le vérifier en calculant le scalaire RmnrsRmnrs.
L’équivalent dans cette métrique
de r = 2GM est le rayon pour lequel
![]() s’annule.
Cela arrive pour :
s’annule.
Cela arrive pour :
|
|
(113) |
On peut avoir deux, une ou zéro solutions en fonction des valeurs relatives de GM2 et p2 + q2. Nous allons considérer les cas séparément.
|
|
Dans ce cas le coefficient
![]() est
toujours positif donc la métrique est régulière
en coordonnées (t, r,
est
toujours positif donc la métrique est régulière
en coordonnées (t, r,
![]() ,F)
sur tous les chemins qui mènent à r = 0.
La coordonnée t est toujours de type temps et r
est toujours de type espace. Mais il y a toujours la singularité
à r = 0, qui est maintenant une ligne de type temps.
,F)
sur tous les chemins qui mènent à r = 0.
La coordonnée t est toujours de type temps et r
est toujours de type espace. Mais il y a toujours la singularité
à r = 0, qui est maintenant une ligne de type temps.
Comme il n’y a pas d’horizon des événements, un observateur peut voyager vers la singularité, revenir et raconter ce qu’il a vu. On connaît ce phénomène sous le nom de singularité nue, du fait qu’elle n’est pas cachée par un horizon. Un examen plus attentif des géodésiques révèle pourtant que la singularité est répulsive.
Les géodésiques de type temps
n’atteignent jamais r = 0, au contraire quand elles
s’approchent, passé un point, elles rebroussent chemin
et repartent en sens contraire. Les géodésiques de type
lumière peuvent atteindre la singularité, ainsi que des
courbes de type temps non géodésiques. Quand r
![]()
![]() ,
la solution se rapproche de l’espace temps plat et nous avons
vu que la structure causale est normale partout.
,
la solution se rapproche de l’espace temps plat et nous avons
vu que la structure causale est normale partout.
Le diagramme de Penrose va donc ressembler à celui de l’espace de Minkowski, sauf pour r = 0 qui est une singularité.
La nudité de la singularité offense et notre pudeur et la conjecture de censure Cosmique qui établit qu’un effondrement gravitationnel de configurations physiques de matière, ne produit jamais de singularités nues.
Ce n’est qu’une conjecture et elle peut être fausse.
Certaines simulations semblent montrer que l’effondrement de configuration “en fuseau” peut conduire à des singularités nues.
En fait, il y n’a pas d’espoir de trouver un trou noir résultant d’un effondrement gravitationnel avec GM2 < p2 + q2. Cette condition conduisant à une énergie totale du trou noir inférieure à l’énergie purement électromagnétique, ce qui voudrait dire que la masse générant le champ électromagnétique serait négative.
Cette solution est donc réputée ne pas avoir de signification physique.
À noter également qu’il n’y a pas de surface de Cauchy convenables (tranches de type espace qui sont coupées par toutes les lignes infinies de type temps) dans cet espace temps, car les lignes de type temps peuvent commencer et finir à la singularité.
C’est une situation qui peut physiquement résulter d’un effondrement gravitationnel. L’énergie électromagnétique est inférieure à l’énergie totale.
Dans ce cas le coefficient de la métrique,![]() (r) est positif pour r grand et r petit et
négatif dans l’intervalle r± =
GM±(G²M²-G(p²+q²))1/2.
(r) est positif pour r grand et r petit et
négatif dans l’intervalle r± =
GM±(G²M²-G(p²+q²))1/2.
La métrique a des singularités de coordonnées à r+ et r-, dans les deux cas elles peuvent être éliminées par un changement de coordonnées comme dans le cas précédent de la métrique de Schwarzschild.

Les surfaces définies par r = r± sont toutes deux nulles et sont en fait des horizons événementiels comme nous allons le préciser.
La singularité à r = 0 est une ligne de type temps, pas une surface de type espace comme dans Schwarzschild.
Pour un observateur tombant de loin dans le trou noir,, r+ joue le rôle de r = 2GM dans la métrique de Schwarzschild : à ce rayon r devient une coordonnée de type temps, et on est aspiré dans la direction des r décroissants.
Des témoins à l’extérieur du trou noir vont observer le même phénomène que dans le cas d’un trou noir non chargé, l’observateur se meut de moins en moins vite et rougit à vue d’œil.
Mais la chute inexorable vers la singularité s’arrête quand on atteint la surface nulle r = r-, où r redevient une coordonnée d’espace et ou le mouvement vers les r décroissants peut être arrêté. Donc nous pouvons éviter la chute fatale vers la singularité r = 0, ce qui était prévisible, car r = 0 est une ligne de type temps et est donc nécessairement dans notre futur. En fait, on a le choix de continuer vers r = 0, où de continuer son chemin dans la direction des r croissants, traverser la surface nulle à r = r-. Alors r va de nouveau être une coordonnée de type temps mais avec une orientation inverse ce qui fait que vous allez être propulsé vers les r croissants.
Vous allez être recraché au-delà de r = r+ émergeant de nulle part, dans le reste de l’univers. De là vous pouvez décider de retourner dans le trou noir (on y prend goût !), un trou noir différent de celui dans lequel vous êtes entré la première fois et répéter le voyage autant de fois que vous voulez. Cette histoire est illustrée par le diagramme de Penrose correspondant, construit en utilisant les coordonnées appropriées et en étendant analytiquement la métrique de Reissner-Nordstrøm aussi loin que possible.
Quelle part la science prend-elle dans ce qui ressemble à de la science-fiction ? Probablement pas beaucoup. Si on imagine le monde, tel que vu de l’intérieur du trou noir par un observateur sur le point de traverser l’horizon à r, vous remarquerez qu’il peut regarder dans le passé et voir l’histoire entière de l’univers externe asymptotiquement plat, du moins vu du trou noir. Mais voir ceci (infiniment long) dans un temps fini de son temps propre, car tout signal qu’il en obtient est infiniment décalé vers le bleu quand il approche de r. Il est donc raisonnable de penser (bien que nous n’en ayons pas la preuve) que toute perturbation qui ne respecte pas la symétrie sphérique dans ce type de trou noir va violemment perturber la métrique et la géométrie de Reissner-Nordstrøm que nous avons décrites. Il est difficile de dire à quoi ressemble vraiment la géométrie, mais nous n’avons pas de raisons valables de penser qu’elle contient une infinité de régions asymptotiquement plates connectées les unes aux autres par divers trous de ver.
Ce cas est appelé la solution extrémale de Reissner-Nordstrøm (ou simplement trou noir extrémal). On peut dire que la masse est contrebalancée par la charge et on peut construire des solutions exactes constituées de trous noirs extrémaux qui restent stationnaires les uns vis-à-vis des autres. D’un côté, un trou noir extrémal est un gadget théorique amusant, ses solutions sont souvent examinées dans le cadre du paradoxe de la perte d’information et dans le rôle des trous noirs en gravité quantique, par contre ces trous noirs sont hautement instables puisqu’une adjonction minime de matière les transforment en catégorie deux.
Les trous noirs extrémaux ne possèdent
qu’un seul rayon, r = GM, car
![]() (r)
= 0.
(r)
= 0.
Ceci représente un horizon événementiel, mais la coordonnée r n’est jamais de type temps, toujours de type espace des deux côtés de l’horizon. La singularité à r = 0 est une ligne de type temps comme dans les autres cas. De ce fait, pour ce type de trou noir, nous pouvons éviter la singularité et continuer notre voyage dans le futur vers d’autres copies de la région asymptotiquement plate, mais avec la singularité toujours sur notre “gauche” comme le montre le diagramme de Penrose.
Nous pourrions encore passer un bon moment en entrant dans les détails des solutions chargées, mais il est temps maintenant de nous intéresser à la catégorie des trous noirs en rotation.
La solution exacte de la métrique est plus complexe, du fait que nous ne pouvons plus utiliser la symétrie sphérique qui permettait de bien simplifier le problème. Ici nous n’avons plus qu’une symétrie axiale (autour de l’axe de rotation), mais cela peut quand même donner des solutions stationnaires (Un vecteur de Killing de type temps). Alors que les solutions de Schwarzschild et Reissner-Nordstrøm ont été découvertes peu de temps après l’établissement de la Relativité générale, la solution pour un trou noir en rotation a été trouvée par Kerr seulement en 1963.
Le résultat, la métrique de Kerr, est donné par la formule un peu plus complexe suivante :
|
|
(114) |
où on a les deux relations :
|
|
|
(115) |
|
|
(116) |
|
Ici a = J/M mesure la rotation du trou (a est le moment cinétique par unité de masse), J est le moment cinétique et M est la masse.
Cela ne pose pas de problème d’introduire des charges électriques et magnétiques q et p, on remplace simplement 2GMr par 2GMr - (q2 + p2) / G. Le résultat est la métrique de kerr-newman. Comme les charges n’apportent pas de phénomènes particuliers, nous poserons q = p = 0 pour l’instant.
Les coordonnées (t, r,![]() ,F) sont appelées coordonnées
de Boyer-Lindquist. C’est direct de vérifier
que quand a
,F) sont appelées coordonnées
de Boyer-Lindquist. C’est direct de vérifier
que quand a
![]() 0,
elles se réduisent aux coordonnées de Schwarzschild. A
"a "constant si M
0,
elles se réduisent aux coordonnées de Schwarzschild. A
"a "constant si M
![]() 0,
nous retrouvons les coordonnées d’un espace temps plat,
mais pas dans les coordonnées polaires habituelles. La
métrique devient :
0,
nous retrouvons les coordonnées d’un espace temps plat,
mais pas dans les coordonnées polaires habituelles. La
métrique devient :
|
|
(117) |
Nous reconnaissons la partie spatiale de cet espace plat en coordonnées ellipsoïdales
Le diagramme ci-dessous montre les coordonnées “ellipsoïdales”. L’axe des "f" est vertical.
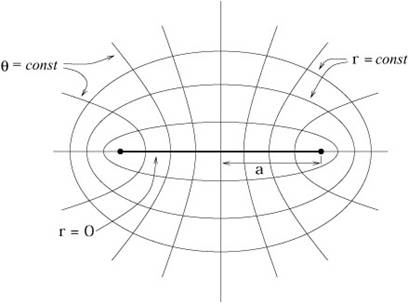
Elles sont reliées aux coordonnées cartésiennes d’un espace 3D par :
|
|
(118) |
Il y a deux vecteurs de Killing de la métrique (114), chacun étant évident, car les coefficients de la métrique sont indépendants de t f, donc zm = ¶t et hm =¶F sont des vecteurs de Killing. Le vecteur hm exprime bien sûr la symétrie axiale de la solution. Le vecteur zm n’est pas orthogonal aux hypersurfaces à t = constante, et n’est en fait orthogonal à aucune hyper surface, la métrique étant stationnaire et non pas statique, (ne change pas avec le temps, mais est en rotation).
De plus la métrique possède ce que nous appellerons un tenseur de Killing C’est un tenseur xm1…mn (0, n) symétrique qui satisfait à :
|
|
(119) |
La métrique elle-même est un exemple de tenseur de Killing ainsi que les produits symétrisés de vecteurs de Killing. Un vecteur de Killing implique un invariant sur le mouvement sur une géodésique, s’il existe un tenseur de Killing sur une géodésique nous allons avoir :
|
|
(120) |
À la différence des vecteurs de Killing, les tenseurs de Killing de rang plus élevé, ne correspondent pas à des symétries de la métrique. En géométrie de Kerr, nous pouvons définir le tenseur (0, 2) :
|
|
(121) |
Dans cette expression les deux vecteurs l et n sont donnés par (on a élevé les indices) :
|
|
(122) |
Les deux vecteurs sont nuls et satisfont :
|
|
(123) |
Signalons, qu’ils sont les vecteurs nuls spéciaux de la classification de Petrov pour cette espace temps. Avec ces définitions, vous pouvez vérifier que xmn est un tenseur de Killing. Réfléchissons sur ce que doit être la structure d’une solution complète de Kerr.
Les singularités semblent apparaître à
la fois à
![]() =
0 et r= 0. Commençons
par
=
0 et r= 0. Commençons
par
![]() =
0. Comme dans la solution de Reissner-Nordstrøm solution il y
a trois possibilités : le type 1 correspondant à
G2M2 > a2,
le type 2 correspondant à G2M2
= a2, et aussi le type 3 correspondant à
G2M2 < a2.
=
0. Comme dans la solution de Reissner-Nordstrøm solution il y
a trois possibilités : le type 1 correspondant à
G2M2 > a2,
le type 2 correspondant à G2M2
= a2, et aussi le type 3 correspondant à
G2M2 < a2.
La dernière caractérise une singularité nue et le cas extrémal G2M2 = a2 est instable comme Reissner-Nordstrøm.
Comme ces cas présentent peu d’intérêt,
et que le temps est compté, focalisons-nous sur le type
1 : G2M2 > a2.
Le terme
![]() s’annule
pour deux valeurs de r, données par :
s’annule
pour deux valeurs de r, données par :
|
|
(7.124) |
Chacun d’eux correspond à une surface nulle qui apparaît comme un horizon des événements. En analysant ces surfaces en s’inspirant du cas Reissner-Nordstrøm, il est facile de trouver des coordonnées qui s’étendent au-delà de l’horizon.
En plus des horizons des événements à r±, la solution de Kerr nous propose une autre surface intéressante. Rappelons-nous que dans les solutions à symétrie sphérique le vecteur de Killing de type temps zm = ¶t s’annule sur l’horizon externe des événements et est de type espace à l’intérieur. Pour vérifier si cela se produit aussi pour la métrique de Kerr nous calculons :
|
|
(125) |
Ceci ne s’annule pas à l’horizon
externe événementiel. En fait à r = r+
(où
![]() =
0), nous avons :
=
0), nous avons :
|
|
(126) |
Donc le vecteur de Killing est toujours de type
espace à l’horizon externe, excepté aux pôles
Nord et Sud (![]() = 0) où il est nul.
= 0) où il est nul.
Le lieu des points ou zm zm = 0 est appelé ergosurface ou surface de limite de staticité, et est donné par :
|
|
(127) |
Tandis que l’horizon externe des événements est donné par :
|
|
(128) |
L’ergosurface apparaît comme la limite
de l’espace temps “statique” à l’approche
du trou. Ce n’est pas un
horizon des évènements, car cette
hypersurface n’est pas de type « nul » :
Un horizon des évènements
est une hypersurface de type nul où un champ de vecteurs de
Killing, s’annule. Dans la métrique de
Kerr, les vecteurs de Killing qui s’annulent sur l’horizon
externe sont (
![]() ) ,
avec zm
= ¶t
et hm
=¶F
et la vitesse angulaire du trou noir à l’horizon
externe,
) ,
avec zm
= ¶t
et hm
=¶F
et la vitesse angulaire du trou noir à l’horizon
externe,
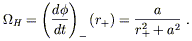
comme cela est décrit, plus loin. Rappelons qu’une combinaison linéaire de vecteurs de Killing est un vecteur de Killing.
Il y a donc une région entre ces deux surfaces, appelée ergosphère (vecteur de Killing ∂t est de type « espace » dans l’ergosphère). A l’intérieur de l’ergosphère, nous nous déplaçons impérativement dans le sens de la rotation du trou noir (la direction F), car il est impossible de rester immobile, mais nous pouvons toujours nous approcher ou nous éloigner de l’horizon des événements (et nous pouvons sortir de l’ergosphère sans problème).
Cet endroit nous réserve quelques surprises que nous passerons en revue plus loin.
Avant de se jeter sur l’étude des
diagrammes de Penrose, essayons de comprendre la nature de la vraie
singularité de courbure, qui n’intervient pas à r
= 0 dans cet espace temps, mais à r=
0. Et comme r² = r2
+ a2cos2![]() est la somme de deux quantités non négative,
elle ne sera nulle que si les deux le sont, soit :
est la somme de deux quantités non négative,
elle ne sera nulle que si les deux le sont, soit :
|
|
(129) |
Ainsi libellé, cela peut paraître
étrange, mais rappelons-nous que r = 0 n’est pas
un point dans l’espace mais un disque. L’ensemble des
points r = 0,
![]() =
=
![]() /2
est en fait un anneau à la périphérie du disque.
/2
est en fait un anneau à la périphérie du disque.
La rotation a modifié la singularité de Schwarzschild en lui donnant la forme d’un anneau.
Étant curieux, nous nous demandons ce qui passe si nous entrons à l’intérieur de l’anneau.
Une analyse minutieuse (que nous ne ferons pas) nous révélerait que nous en sortirions vers un autre univers asymptotiquement plat mais, pas une copie identique à celui dont nous venons.
Le nouvel espace temps est décrit par une
métrique de Kerr avec r < 0. Il en résulte
![]() ne
s’annule jamais et qu’il n’y a donc pas d’horizons
(des événements).
ne
s’annule jamais et qu’il n’y a donc pas d’horizons
(des événements).
Le diagramme de Penrose associé ressemble à celui de Reissner-Nordstrøm, sauf qu’on peut traverser la singularité.

Cette fois ci en plus des étranges régions
asymptotiquement plates distinctes de la nôtre, mais connectées
à la nôtre par notre trou noir, nous avons droit à
une pathologie très particulière dans la région
voisine de la singularité en anneau : l’existence
de courbes de type temps
fermées. Si on considère des trajectoires
qui tournent selon la coordonnée F,
à
![]() et
t constants et pour r une valeur négative
faible, alors le ds² le long d’un tel chemin vaut :
et
t constants et pour r une valeur négative
faible, alors le ds² le long d’un tel chemin vaut :
|
|
(130) |
Il peut être négatif pour r petit et négatif. Comme ces chemins sont fermés, ce sont évidemment des boucles temporelles, ce qui veut dire que vous pouvez vous rencontrer vous-même dans le passé avec tout ce qui s’ensuit2.
Certes, tout ce que nous disons au sujet de l’extension analytique de Kerr est sujet aux mêmes objections que celles que nous avons mentionnées pour Schwarzschild et Reissner-Nordstrøm. Il paraît hautement improbable qu’un effondrement gravitationnel réel puisse conduire à ces espaces-temps pour le moins bizarres. Néanmoins, il est toujours utile de considérer ces solutions exactes.
De plus pour la métrique de Kerr, il se passe des choses également étranges, même si nous restons à l’extérieur de l’horizon des événements, regardons cela de plus près.
Commençons par nous intéresser à
la vitesse angulaire du trou. Évidemment, la définition
conventionnelle doit être modifiée, avant d’appliquer
quoi que ce soit à quelque chose d’aussi abstrait que la
métrique de l’espace temps. Considérons le sort
d’un photon, émis dans la direction F,
à un rayon r dans le plan équatorial (![]() =
=
![]() /2)
d’un trou noir de Kerr. A l’instant d’émission
son impulsion ne comporte pas de composantes dans les directions r
et
/2)
d’un trou noir de Kerr. A l’instant d’émission
son impulsion ne comporte pas de composantes dans les directions r
et
![]() ,
cette condition (composantes r et
,
cette condition (composantes r et
![]() =0),
s’écrit :
=0),
s’écrit :
|
|
(131) |
Si on résout, on obtient :
|
|
(132) |
Si nous évaluons l’expression sur l’hypersurface externe de l’ergosphère de la métrique de Kerr, nous avons gtt = 0 et les deux solutions sont :
|
|
(133) |
La solution non nulle a le même signe que a. Nous pouvons l’interpréter comme le fait que le photon tourne dans le même sens que le trou noir. La solution zéro montre que le photon à contre courant est immobile dans ce système de coordonnées. (Ce n’est pas la solution complète de la trajectoire, seulement le constat que la vitesse instantanée est nulle).
Ceci est un exemple de l’entraînement des référentiels inertiels auquel nous avons fait allusion avant. Cet exercice a pour but de montrer que les particules massives qui se déplacent à une vitesse inférieure à celle de la lumière sont entraînées par la rotation du trou noir dès qu’elles sont derrière l’horizon de Killing. Cet entraînement se poursuit quand nous nous approchons de l’horizon des événements à r+. Nous pouvons définir la vitesse angulaire de l’horizon des événements lui-même, WH, comme étant la vitesse angulaire minimum d’une particule à l’horizon. De (132) nous trouvons que :
|
|
(134) |
Penchons-nous maintenant sur le mouvement géodésique, notre approche peut être simplifiée en considérant les quantités conservées associées aux vecteurs de Killing zm= ¶tet hm= ¶f. Pour notre propos, nous nous limiterons au cas des particules massives, dont nous considérerons la quadri-impulsion :
|
|
(135) |
Où m est la masse au repos de la particule : Appliquons la condition de conservation à l’énergie réelle et au moment cinétique de la particule :
|
|
(136) |
et
|
|
(137) |
Elles diffèrent des définitions précédentes des quantités conservées où E et L étaient l’énergie et le moment cinétique par unité de masse. La conservation s’applique naturellement dans les deux cas. Le signe moins de la définition de E est justifié par le fait qu’à l’infini et zmet pm sont de type temps, donc leur produit scalaire est négatif, et que nous voulons une énergie positive.
A l’intérieur de l’ergosphère cependant, zm devient de type espace on peut imaginer une particule pour qui :
|
|
(138) |
Cet état négatif qui paraît contrariant, peut se retourner à notre avantage en considérant que si toutes les particules à l’extérieur de l’horizon de Killing doivent avoir des énergies positives et si une particule à l’intérieur de l’ergosphère a une énergie négative soit, elle reste à l’intérieur de l’horizon de Killing sur une géodésique soit, elle va être accélérée jusqu’à acquérir une énergie positive et dans ce cas s’échapper.
Ceci nous procure un moyen d’extraire de l’énergie d’un trou noir en rotation. La méthode est appelée procédé de Penrose. L’idée est simple (la réalisation pratique l’est moins). Partant de l’extérieur de l’ergosphère, vous vous munissez d’un objet lourd et encombrant, dont vous souhaitez vous débarrasser définitivement. Muni de cet accessoire, vous bondissez vers le trou noir. Si la quadri-impulsion du système formé de vous et du rocher est p(0)m, alors l’énergie E(0) = - zm p(0)m est certainement positive et conservée sur la géodésique. Dès que vous entrez dans l’ergosphère, débarrassez-vous de ce rocher en en le projetant violemment, de toutes vos forces d’une certaine manière très particulière. Si nous appelons votre impulsion p(1)m et p(2)m, celle du gros rocher, à l’instant où vous projetez le rocher, l’impulsion globale est conservée (cf relativité restreinte) :
|
|
(139) |
En contractant avec le vecteur de Killing zm il résulte :
|
|
(140) |
Si nous supposons que vous êtes arbitrairement fort et adroit, vous pouvez vous arranger pour que votre lancer soit tel que E(2) < 0, conformément à (158).
|
|
Penrose put donc montrer que si vous suivez une trajectoire initiale bien particulière et opérez un lancer comme indiqué, vous allez ressortir de l’ergosphère selon une géodésique et comme l’énergie est conservée tout le long du chemin finalement vous allez avoir :
|
|
(141) |
C’est-à-dire plus d’énergie (mais un rocher en moins) que quand vous êtes rentré.
Mais les trous noirs rasent gratis (rappelons qu’ils n’ont pas de poils), car l’énergie acquise a été empruntée au trou noir. En fait le procédé de Penrose permet d’extraire de l’énergie au trou noir en l’empruntant à son moment cinétique (ce qui fait décroître son moment cinétique). Il faut jeter l’objet dans le sens contraire de la rotation pour que ça marche.
Plus précisément, définissons un nouveau vecteur de Killing :
|
|
(142) |
Sur l’horizon externe cm est nul et tangent à l’horizon. Cela découle de zm = ¶t, hm = ¶F, et de la définition (134) de WH. Le fait que la particule d’impulsion p(2)m traverse l’horizon vers le futur s’exprime simplement par :
|
|
(143) |
En le substituant dans les définitions de E et L, nous voyons que cette condition est équivalente à :
|
|
(144) |
Comme nous nous sommes arrangés pour que E(2) soit négative et WH positif, nous voyons que la particule doit avoir un mouvement angulaire négatif, tourner en sens contraire du trou. Une fois que vous êtes sorti du trou, le rocher largué vers l’horizon événementiel, la masse et le moment cinétique du trou se voient modifiés par la contribution négative du rocher.
|
|
(145) |
J représente le moment cinétique du trou noir, il vaut :
|
|
(146) |
Nous ne le justifierons pas (voir Wald pour l’explication). Du coup (144) nous indique la limite maximum de décroissance du moment cinétique du trou noir :
|
|
(147) |
Si nous atteignons cette limite, tandis que
le très gros rocher que nous jetons devient de plus en
plus “nul”, nous atteignons l’optimum dans lequel
![]() J
=
J
=
![]() M/WH.
M/WH.
Nous allons maintenant utiliser ces idées pour prouver un résultat très important. Même si on peut utiliser le procédé de Penrose pour extraire de l’énergie d’un trou noir on ne peut jamais faire décroître l’aire de l’horizon des événements. Pour la métrique de Kerr, on peut par un calcul immédiat (projection l’élément linéaire et le volume métrique,..) calculer l’aire de l’horizon des événements.
|
|
(148) |
Pour montrer qu’il ne peut pas décroître, il est plus adapté de travailler en termes de masse irréductible du trou noir défini par :
|
|
(149) |
On peut différentier cette expression et on obtient après un peu de transpiration :
|
|
(150) |
Nous pensons que les facteurs de G sont corrects, mais cela ne ferait pas de mal de vérifier. Alors la limite (147) devient :
|
|
(151) |
La masse irréductible, comme son nom l’indique, ne peut pas être réduite. Il s’ensuit que l’énergie maximum que nous pouvons extraire d’un trou noir en rotation jusqu’à provoquer son arrêt est :
|
|
(152) |
Cette énergie extraite on obtient un trou noir de Schwarzschild de masse Mirr. Le mieux qu’on puisse espérer avec le trou noir extrémal de Kerr est d’environ 29% de son énergie totale (ce qui est appréciable).
L’irréductibilité de Mirr implique que l’aire A ne peut jamais décroître. De (149) et (150) nous tirons :
|
|
(153) |
qui peut être réécrit :
|
|
(154) |
où nous avons introduit :
|
|
(155) |
La quantité![]() est appelée la gravité de surface du trou
noir.
est appelée la gravité de surface du trou
noir.
C’est en partant d’équations comme (154), qu’on a commencé à faire le rapprochement entre les trous noirs et la thermodynamique. Considérons la première loi de la thermodynamique :
|
|
(156) |
Il est naturel d’interpréter le terme
WH![]() J comme le travail que nous produisons dans le trou noir
en y jetant des objets.
J comme le travail que nous produisons dans le trou noir
en y jetant des objets.
Ainsi l’analogie avec la thermodynamique
commence à prendre forme si nous assimilons l 'aire A
à l’entropie S, et la gravité de surface
![]() à
8
à
8![]() G fois la température T. En fait
dans le contexte de la Relativité générale
l’analogie est essentiellement parfaite.
G fois la température T. En fait
dans le contexte de la Relativité générale
l’analogie est essentiellement parfaite.
La loi zéro de la thermodynamique dit qu’en équilibre thermique la température est la même partout dans le système. La proposition équivalente, pour les trous noirs, est que la gravité de surface est constante sur l’horizon entier (vrai). Nous avons vu que la première loi (156) est équivalente à (154).
La seconde loi, qui stipule que l’entropie ne décroît jamais, correspond au fait que l’horizon ne décroît jamais.
Enfin la troisième loi qui stipule qu’il
est impossible d’atteindre T = 0 dans n’importe
quel processus physique doit impliquer qu’il est impossible
d’atteindre
![]() =
0 dans n’importe quel processus physique. Il apparaît
que
=
0 dans n’importe quel processus physique. Il apparaît
que![]() = 0 correspond aux trous noirs extrémaux (soit de Kerr où
de Reissner-Nordstrøm) laissant apparaître des
singularités nues. Par cela la troisième loi se réfère
à la censure cosmique
= 0 correspond aux trous noirs extrémaux (soit de Kerr où
de Reissner-Nordstrøm) laissant apparaître des
singularités nues. Par cela la troisième loi se réfère
à la censure cosmique
Le chaînon manquant était que les corps noirs thermodynamiques réels devaient produire le rayonnement du corps noir caractéristique, fonction de leur température. Avant la découverte de Hawking on pensait que les trous noirs ne rayonnaient pas du tout, qu’ils étaient vraiment noirs.
Historiquement c’est Bekenstein qui le premier a eu l’idée que les trous noirs pouvaient se comporter en honnêtes corps noirs, avec leur rayonnement dépendant de leur température, à la clé. Ceci chagrinait Hawking qui, en voulant prouver que c’était faux, établit le contraire. L’analogie thermodynamique se confirme être plus actuelle que jamais, même si pour être honnête personne ne sait très bien pourquoi.
1En fait nous nous référons à l’ergosurface « externe », il en existe une autre interne qui présente un intérêt moindre.
2Note
J. Fric: Le ds² de l’équation (130) est très
incomplet (vous pouvez le vérifier sur la métrique de
Kerr). Il ne prend-on compte que les termes prépondérants
au premier ordre quand r est petit et négatif pour
![]() voisin
de
voisin
de
![]() /2.
Une analyse plus détaillée montre que la région
où on trouve des boucles temporelles correspond à gφφ
≤ 0. Cette région à une forme torique (à
section non circulaire) dont l’équateur intérieur
est la singularité. Une conséquence de l’existence
de cette région est que dans toute la région(en
général appelée région III) sous
l’horizon intérieur, y compris toute la région
où les « r » sont négatifs, la
causalité est violée de façon non triviale
(voir article de B. Carter, Physical Review 1968).
/2.
Une analyse plus détaillée montre que la région
où on trouve des boucles temporelles correspond à gφφ
≤ 0. Cette région à une forme torique (à
section non circulaire) dont l’équateur intérieur
est la singularité. Une conséquence de l’existence
de cette région est que dans toute la région(en
général appelée région III) sous
l’horizon intérieur, y compris toute la région
où les « r » sont négatifs, la
causalité est violée de façon non triviale
(voir article de B. Carter, Physical Review 1968).