Des Défauts dans l’Univers

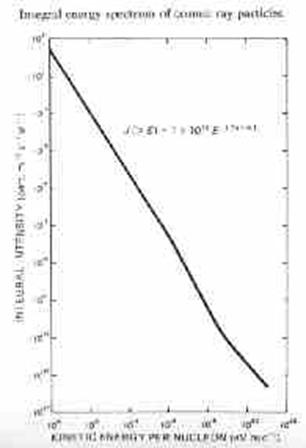
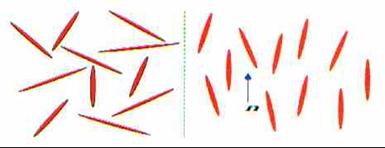1. PRELIMINAIRES

1.1 Les particules standards.

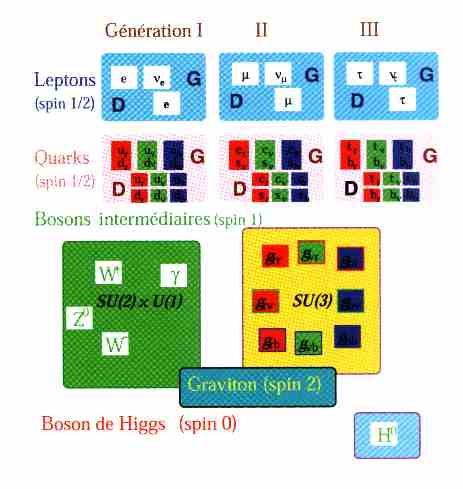
Résumé de l’ensemble de toutes les particules qui composent le modèle standard, incluant les trois familles (générations), les quatre interactions, ainsi que la particule de Higgs responsable de la brisure de symétrie.

Les trois familles de particules, à part les neutrinos, apparaissent sous deux formes notées “D”et “G” (pour Droite et Gauche), ce qui correspond à l’une des symétries de la nature (une autre est l’hélicité).

Cette présentation de l’ensemble des particules de la nature est due originellement à G. T’Hooft.

1.2 Energies

Dans un système physique, chaque particule possède une quantité d’énergie qui peut être sous l’une ou l’autre des deux formes suivantes, ou un mélange des deux :

Energie cinétique (agitation thermique, mouvement)

Energie potentielle (interactions électromagnétique, faible, forte, gravitationnelle et du champ de Higgs)

1.3 Phases et symétries

Lorsque l’énergie cinétique devient faible devant l’énergie potentielle les forces d’interaction entre les particules dominent les forces de mouvement et l’ensemble du système se “fige” --> changement de phase + brisure de symétrie.

1.4 Transitions et défauts

Le changement de phase prend un certain temps et ne se fait pas partout simultanément. Il démarre en différents endroits dans le système et se propage. Aux endroits ou il y a rencontre, il peut y avoir des incompatibilités (une même particule peut être sollicité de deux façons antagonistes), ce qui forme des défauts.

1.5 Le vide

Définitions : “Absence de tout objet”. (Littéraire)

“C’est l’état possédant le moins d’énergie possible”. (physique des particules)

1.7 Super-symétrie

Les bosons messagers des interactions, sont grégaires, ils tendent à se placer tous dans le même état.

Les fermions, constituants de la matière, n’acceptent pas de partager un même niveau d’énergie.

La super-symétrie entraîne l’association d’un boson et d’un fermion.

Comme les deux partenaires doivent avoir la même masse, les particules actuellement connues ne font pas l’affaire. Il faut donc supposer que cette symétrie est brisée et qu’il existe dans la nature des particules que nous ne connaissons pas encore.

2. LES MECANISMES DE HIGGS ET DE KIBBLE.

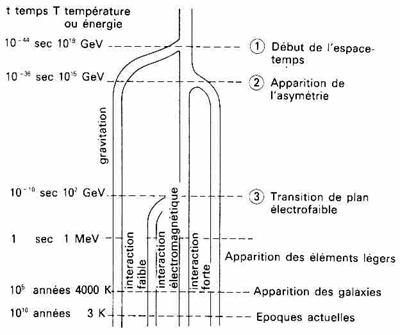
Au temps de Planck, la température de l’Univers est celle de Planck ( 10²⁰ GeV ). Elle décroît ensuite (par l’expansion de l’Univers) entraînant une succession de transitions de phases.

2.1 Le mécanisme de Peter HIGGS

P. HIGGS a proposé un mécanisme qui permet d’attribuer une masse aux vecteurs d’une interaction.

2.1.1 Analogie avec les cristaux liquides

Les molécules allongées des cristaux liquides sont orientés au hasard à haute température et s’alignent à basse température dans la phase nématique.

Dans le cas le plus simple, un seul axe moléculaire détermine l’orientation. Cette direction est appelée le “directeur” et noté “n” sur la figure.

Dans ce type de cristal, la taille de chaque molécule ne varie pas, par contre leur orientation peut changer d’un point à un autre. La moyenne des orientations peut être nulle ou privilégier une direction. L’alignement est caractérisé par deux nombres : l’angle de l’alignement et l’amplitude moyenne. Ceci est un champ de type “complexe” représenté par une flèche variable d’un point à un autre.

A très haute température, les molécules ne s’alignent pas : l’amplitude moyenne est nulle (flèche de taille 0, sans orientation).

A plus basse température, l’énergie potentielle (force d’interaction entre molécules) domine l’énergie cinétique : les molécules s’alignent et la flèche devient maximale. Par contre l’angle de l’alignement est quelconque. Pour le potentiel, cela se traduit par une vallée à la même hauteur pour toutes les valeurs de l’angle, avec une bosse pour une orientation nulle.

En physique des particules, les molécules et leurs orientations sont remplacées par un champ dit : champ de Higgs.

Son potentiel mesure l’énergie qu’il contient.

L’analogue d’une particule dans un cristal est une onde sonore. Elle se propage d’autant plus facilement que les molécules sont moins bien alignées. Lorsque l’orientation est nulle (molécules dans toutes les directions) la propagation se fait sans résistance (cas de la haute température). Après la transition de phase, il y a une orientation importante (couplage entre molécules) entraînant une résistance à la propagation c’est à dire une inertie.

L’inertie donne une mesure de la masse de l’objet qui se propage. On peut donc dire que dés que la symétrie est brisée, la masse n’est plus nulle puisqu’il y a résistance au mouvement.

De la même façon, toutes les particules qui interagissent avec le champ de HIGGS, acquièrent une masse dès que celui-ci n’est plus nul.

2.1.2 La transition de phase vue dans l’espace du champ de Higgs.

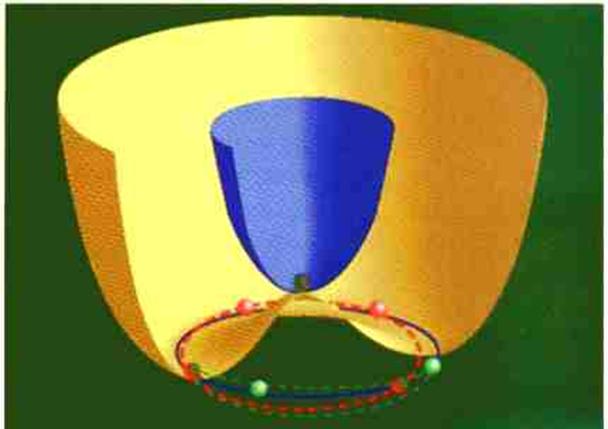
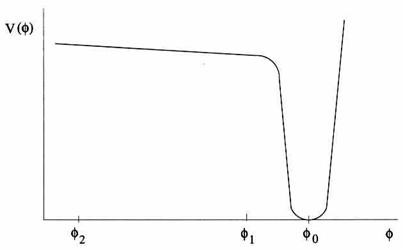
En bleu, le potentiel du champ de Higgs pour T > T_c.

En jaune, le potentiel du champ de Higgs pour T < T_c.

A haute température le champ prend une valeur nulle (bille grise au centre). C’est un état à haut degré de symétrie.

Pour minimiser son énergie, le champ cherche à rester au minimum du potentiel.

Durant la transition de phase, l’Univers entier se refroidit, et le potentiel prend une nouvelle forme (surface jaune).

Cette surface possède un cercle de minima (cercle bleu).

Pour minimiser son énergie, le champ doit choisir une position sur ce cercle. Cette position impose une orientation particulière qui brise la symétrie.

2.2 Le mécanisme de KIBBLE

Au cours de l’évolution de l’Univers, des domaines non corrélés ont dû apparaître où le champ de HIGGS a pris des valeurs de vide différentes. La taille de ces domaines a augmenté jusqu’à leur rencontre.

KIBBLE a mis en évidence que les vides différents de ces domaines ne pouvaient pas se raccorder. Cela génère des défauts aux interfaces ou le champ de HIGGS ne peut pas minimiser son énergie.

Ces interfaces sont constituées de “faux vide” (le vrai vide étant celui qui existe de chaque côté de l’interface).

La nature des défauts dépend des symétries du champ de Higgs initial.

Si le champ de HIGGS a une symétrie circulaire, il va s’ajuster en concentrant les discontinuités le long de lignes, plutôt que de murs. C’est ce qu’on appel les “cordes cosmiques”. Elles sont extrêmement fines et constituées de faux vide.

La structure du champ de HIGGS peut être encore beaucoup plus compliquée et amener d’autres types de défauts comme des défauts ponctuels appelés “monopôles” , ou même des défauts dits “semi-topologiques” appelés “textures”.

A part les “textures”, les défauts préservent l’état de symétrie non brisée, c’est à dire le faux vide qui régnait avant le transition de phase. Ces régions devraient contenir d’énormes quantités d’énergie.

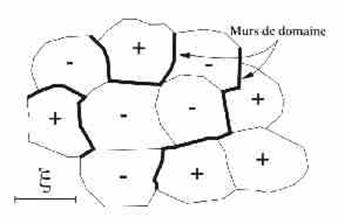
2.3 La longueur de corrélation (Ksi)

Un état de vide est caractérisé par le fait que le champ de HIGGS prend, dans cet état, une valeur qui correspond à un minimum du potentiel. Si les minima ont des énergies différentes on parle de minima locaux. Dans cette situation le vrai vide sera l’état dans lequel l’énergie est minimisée de façon globale (il ne doit pas exister de configuration d’énergie moindre).

2.3.1 Transition de phase discontinue

Pour une température inférieure à la température critique, des bulles de vrai vide apparaissent dans un environnement de faux vide (nucléation). La phase du champ de HIGGS est différente d’une bulle à l’autre. Les bulles vont croître et finir par se rencontrer (leur vitesse de croissance est au moins égale à celle de l’expansion de l’Univers avant l’inflation). Lorsqu’elles se rencontrent des défauts (monopôles, cordes, domain walls) peuvent apparaître.

2.3.2 Transition de phase continue

Le champ de Higgs change de valeur de manière continue quand la température décroît, mais le phénomène étant aléatoire, les valeurs peuvent être différentes dans des régions éloignées d’ou là encore création de défauts.

La longueur de corrélation est la longueur caractéristique du réseau de cordes ainsi formé. Elle dépend de :

- la distance typique entre deux bulles au moment où celles-ci apparaissent;

- la probabilité de nucléation;

- la vitesse d’expansion des bulles;

- la probabilité que les orientations s’ajustent de manière à former un défaut.

3. ILLUSTRATIONS EN LABORATOIRE

On considère habituellement que la matière peut se présenter sous trois phases : solide, liquide, gazeuse. Il y a cependant des états qui ne répondent pas à cette classification : la mayonnaise, le lait concentré etc.

3.1 Les cristaux liquides

Ce sont des composés organiques avec des phases intermédiaires entre le solide et le liquide : ils peuvent couler comme un liquide tout en ayant les propriétés des solides, telle une structure moléculaire orientée. Par exemple le cholestéryl de benzoate présente deux points de fusion : à 145,5 °C il passe de l’état solide à l’état de liquide brumeux et à 178,5 °C il devient un liquide clair.

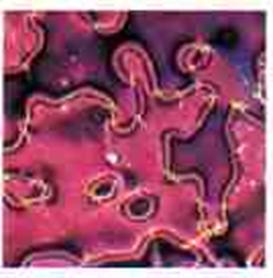
3.1.1. Echantillon de cristal liquide nématique

(Image obtenue au microscope à polarisation croisée.)

Au voisinage d’un défaut le directeur change de façon très abrupte puisqu’au lieu même du défaut il ne peut être défini.

L’absence de directeur est un défaut. De même, le lieu de localisation d’une corde cosmique (le défaut), est l’endroit où il n’y a pas d’orientation du champ de HIGGS définie puisque celui-ci doit rester dans le faux vide ou son amplitude est nulle (phase symétrique).

Dans un cristal comme en cosmologie, les défauts peuvent se présenter sous plusieurs formes : ponctuels, linéiques ou plus complexes.

L’omniprésence des défauts linéiques dans les cristaux liquides, est à l’origine de la dénomination “nématique” (fil).

Sur la photo, on voit les bosses de Schlieren. Les défauts ponctuels sont souvent reliés par des lignes ou le directeur n’est pas non plus défini. Ce sont les équivalents des monopôles reliés par des cordes cosmiques. Ces différents défauts peuvent interagir entre eux et même s’annihiler.

Les défauts d’un cristal liquide ne sont pas des objets rigides. Ils peuvent se mouvoir et être influencés par des sources extérieures (champ magnétique, gravitation ...). Ils peuvent aussi interagir entre eux.

Le nombre de défauts produits dans chaque bulle de nématique issue de la transition a été mesuré. Les résultats obtenus sont tout à fait en accord avec la théorie pour la production de cordes et de boucles cosmiques.

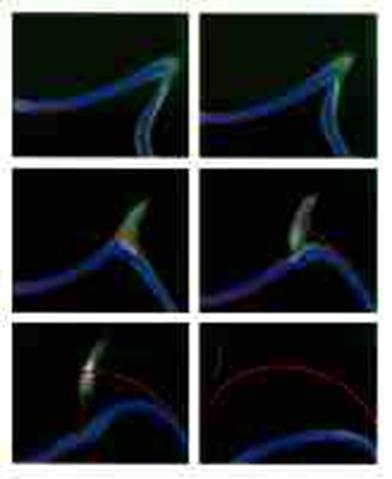
3.1.2. Intercommutation de deux défauts linéiques dans un cristal liquide nématique.

Cette séquence montre deux défauts qui s’approchent, fusionnent, formant un noeud qui, étant topologiquement instable, se désintègre, conduisant à deux défauts ayant échangé leurs extrémités.

4. DEFAUTS COSMIQUES

4.1 Les rideaux (membranes cosmiques)

La plupart des théories actuelles n’en prédisent pas.

Si la brisure de symétrie permet de former des membranes, alors on en trouvera une par volume d’horizon.

Leur densité surfacique, est caractérisée par l’énergie (température) au moment de la transition de phase ( 10⁵³ gr/cm² )

Leur densité est toujours très supérieure à la densité critique de l’Univers.

4.2 Les cordes

Ce sont les seuls défauts compatibles avec l’ensemble des observations actuelles. Elles peuvent exister sous la forme de petites boucles, qui satisfont aux critères requis pour la matière noire.

4.2.1. Apparition des cordes cosmiques.

Dans chaque région de l’espace, la direction de la flèche du champ de HIGGS prend des valeurs comprises entre 0 et 360°.

Lorsque le champ à le choix parmi toutes les valeurs, c’est qu’on est resté en ce point, dans l’état d’avant la transition de phase (champ nul, symétrie totale).

A haute température, le champ de HIGGS est nul partout.

Lorsque la température décroît en dessous du niveau critique, il choisit une orientation parmi celles qui sont possibles. Il existe une longueur de corrélation qui définie la distance supérieure ou cette valeur du champ va s’imposer, indépendamment de celle choisie dans les régions voisines. Il se forme ainsi un ensemble de domaines de tailles équivalentes ou le champ de HIGGS à des valeurs différentes. Lorsque ces domaines se rencontrent, au minimum 3 par 3, ils forment des arêtes aux interfaces. Ces arêtes ne pouvant adopter les valeurs des domaines adjacents, la transition n’a pas lieu pour elles et elles restent dans l’état énergétique du faux vide. Elles possèdent donc beaucoup plus d’énergie que les domaines qui sont passés par la transition de phase.

L’épaisseur d’une corde est approximativement l’inverse de la masse de la particule de HIGGS (10^-30 m ).

L’énergie par unité de longueur, vaut environ le carré de cette masse (10¹⁹ tonnes / m)

La force gravitationnelle qu’exerce une corde est au pire 10^{-6 .}

Cordes locales : leur énergie est confinée dans un coeur très fin.

Cordes globales: plus épaisses elles génèrent une interaction à longue portée entre les cordes elles-mêmes.

4.2.2. Modèle de cordes cosmiques

Comme tout objet contenant de l’énergie, elles peuvent agir par gravitation sur la matière.

Plongeons un fil dans de l’eau :

- Immobile, il ne se passe rien.

- Lorsqu’il se déplace, il se forme un sillage.

Si une corde traverse une région contenant de la matière, elle forme un sillage. Cela conduit à la formation de régions en forme de plan. Les catalogues de galaxies peuvent s’interpréter avec de tels feuillets.

Les cordes sont des objets très curieux : bien que très massives, elles ne produisent pas de champ gravitationnel statique. L’interaction entre deux cordes produit un phénomène de reconnexion : deux objets distincts deviennent indiscernables. Ce mécanisme permet de produire des boucles dotées d’une grande énergie cinétique (reconnexion). Ce processus permet aussi au réseau de perdre de l’énergie.

Les cordes cosmiques sont les analogues des lignes de vortex dans les cristaux liquides. Elles sont prédites par la physique des particules (très hautes énergies).

Lorsqu’une particule s’approche d’une corde, elle se trouve piégée. Si la particule est chargée, alors il peut se créer un courant électrique. La masse des particules provient de leur couplage au champ de Higgs qui forme la corde. On s’attend à ce que cette masse soit comparable à celle du champ de Higgs. Donc le courant doit être de l’ordre de grandeur de la masse de la particule de Higgs (10²⁰ A). Malgré son importance, cette intensité ne semble pas modifier le comportement des cordes.

La génération de champs magnétiques dans le plasma primordial par ces cordes n’a été que très peu étudiée.

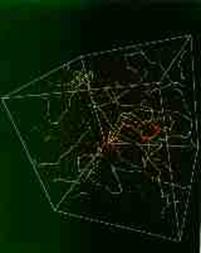
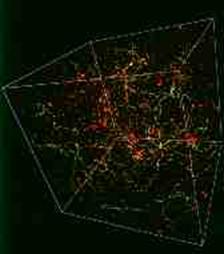
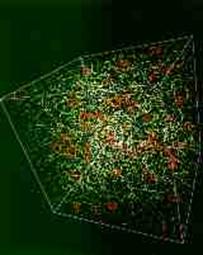
4.2.3. Distribution des cordes

Quand la transition de phase se termine, les phases prennent des valeurs aléatoires dans des régions séparées d’au moins la longueur de corrélation ( l ). Les simulations numériques montrent que les cordes se distribuent au hasard suivant un pas égal à l . Elles se présentent sous la forme de lignes brisées erratiques. En conséquence, si une corde passe par deux points de l’espace séparés d’une distance R, la longueur de corde qui les relie sera : R² / l . La longueur de corrélation est donc importante pour calculer la densité d’énergie due aux cordes.

Distribution initiale Univers jeune Univers actuel

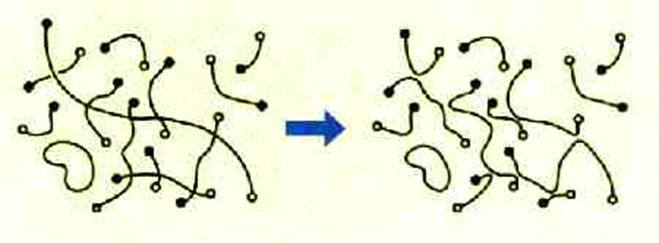
Les cordes évoluent par reconnexions, formant ainsi des boucles de plus en plus petites. Il arrive un moment ou la taille et la densité sont telles qu’elles ne peuvent plus se rencontrer.

Elle se contracte sous l’effet de sa tension, oscille (elle n’était pas circulaire au départ) et perd une quantité importante d’énergie par rayonnement gravitationnel. Elle se désintègre par rayonnement gravitationnel.

Lors de l’expansion, la structure des cordes sera “lissée” sur des échelles plus petites que celle de l’horizon. Les simulations montrent que les cordes infinies contribuent pour 80% à l’énergie du réseau. Cela veut dire qu’au moins 20% du total est sous forme de boucles dont la distribution en taille se trouve indépendante de la longueur de corrélation l.

Le réseau de cordes obtenu est “invariant d’échelle”, c’est à dire qu’il reste identique lorsqu’on modifie la longueur de corrélation l .

L’évolution du système de cordes est régulé par deux effets :

- l’interaction entre cordes conduit à la production de boucles ( “inter commutation” ).

- Comme ces boucles sont oscillantes, elles perdent leur énergie sous forme de rayonnement gravitationnel.

4.2.4 Les vortons

Les cordes qui portent des courants produisent de nouveaux objets appelés vortons.

Si la corde est initialement parcourue par un courant, le début est le même. Lorsque la taille de la corde diminue, le courant augmente, il a pour effet de réduire la tension de la corde et de l’entraîner en rotation. La rotation induit une force centrifuge qui va augmenter en même temps que la tension de la corde va diminuer. La force centrifuge va devenir plus importante que la tension et la corde va finir par arrêter sa contraction. Cet état d’équilibre de la boucle constitue un vorton. Il ne se distingue en rien d’une particule élémentaire quoique beaucoup plus lourd et plus petit. Il a une charge et il se comporte comme de la matière ordinaire non baryonique.

Si ces objets ont été produits,, alors ils ont dominés l’Univers du fait de leur stabilité.

Ce dernier point en fait un obstacle majeur aux modèles cosmologiques utilisant des cordes supraconductrices pour la formation des grandes structures.

4.3 Les monopôles

Les champs électriques et magnétiques ne sont pas symétriques :

- une charge électrique peut exister seule.

- une charge magnétique n’a jamais été observée. Il y a toujours une paire de pôles.

Dans les théories de grande unification, cette symétrie absente des équations de Maxwell, réapparaît. Les pôles nord et sud sont particule et anti-particule l’un de l’autre. Ils peuvent s’annihiler. Ils sont topologiquement stables : ce sont des défauts topologiques.

Ils ne sont produits que sous certaines conditions comme par exemple :

- Si la symétrie qui reste après la transition de phase est circulaire (c’est celle de l’électromagnétisme !)

- Aux très hautes températures de l’Univers primordial, les conditions étaient remplies, il y a donc eut formation de monopôles.

Malheureusement ils sont produits en très grande quantité, ce qui pose un problème cosmologique.

- Dès leur formation les monopôles deviennent non relativistes car ils sont très lourds et interagissent fortement avec la matière. Leur densité décroît donc comme celle de la matière; soit comme l’inverse du cube du facteur d’échelle de l’Univers.

La solution à ce problème, envisagée aujourd’hui, est une période d’inflation cosmique qui a permis de diluer (jusqu’aux valeurs observées) tous les vestiges primordiaux et en particulier les monopôles.

- D’autres scénarios permettent de combattre la surpopulation des monopôles en particulier : les monopôles ne sont pas formés seuls mais ils sont liés à des cordes cosmiques. Ou bien ils peuvent cohabiter avec des membranes cosmiques qui les ramassent en les absorbant.

4.4 Défauts hybrides

Dans les modèles de grande unification, ce n’est en général pas une, mais plusieurs brisures de symétrie qui se produisent. On peut donc s’attendre à deux situations :

- des défauts de types différents sont produits à chaque transition.

- des défauts vont être produits accrochés les uns aux autres au fur et à mesure que les transitions de phase se succèdent. Dans ce cas il s’agit de défauts hybrides. Exemple : une corde et deux monopôles . Ceci veut dire que les cordes qui vont se former peuvent être instables pour que la probabilité pour qu’une corde soit cassée par l’apparition d’une paire de monopôles existe.

- de la même façon il peut y avoir des schémas de brisure de symétrie au cours desquels des membranes et des cordes sont produites successivement. Dans ce cas nous rencontrerons des morceaux de membranes bordés par des cordes. Les membranes pouvant être trouées par l’apparition de boucles de cordes.

Toutes ces configurations sont transitoires et finalement il ne reste plus rien à condition que ça se passe assez vite.

4.5 Interactions entre défauts différents

4.5.1. Cas des défauts produits au cours de deux transitions différentes :

- première transition > génération de monopôles ;

- deuxième transition > le flux magnétique de ces monopôles se confine à l’intérieur de tubes de flux, c’est à dire des cordes cosmiques locales.

Les cordes s’effondrent sur elles-mêmes du fait de leur tension et les monopôles sont annihilés.

Evolution du réseau de cordes reliant des monopôles.

4.5.2. Cas des défauts produits au cours de la même transition de phase

Si des membranes sont formées accompagnées de monopôles, la tension superficielle des membranes les fera se déplacer. Elles rencontreront des monopôles. Lorsqu’ils sont mis en présence, le monopôle est absorbé par le mur. Le monopôle forme un état lié avec le mur. Or à l’intérieur du mur le monopôle n’a plus de raison topologique d’être stable : il se désintègre. Rapidement le réseau de murs va faire disparaître tous les monopôles.

Les murs disparaissent lorsqu’ils proviennent d’une brisure de symétrie imparfaite. Dans ce cas, l’énergie est différente des deux côtés du mur ce qui entraîne une différence de pression. Le mur se déplace alors d’une façon extrêmement rapide et disparaît de l’Univers observable (rempli alors par la configuration de moindre énergie).

Ces phénomènes peuvent être simulés dans l’hélium 3 superfluide.

4.6 Inflation

L’inflation explique entre autres choses, la “platitude” de l’Univers (C’est la seule solution connue aujourd’hui).

Le champ responsable de l’inflation génère des fluctuations quantiques primordiales.(concurrents des défauts ?)

Selon les théories de physique des particules, les défauts sont produits de façon générique, alors qu’amorcer une phase d’inflation paraît bien peu naturel, car cela contraint à un ajustement très précis des paramètres .

Dans les tous premiers instants : domination d’un champ scalaire qui va tendre vers son énergie minimale dans un Univers vide (ni lumière ni matière). La densité d’un tel champ dépend de son énergie cinétique (évolution), autant que de son énergie potentielle.

4.6.1 Evolution du champ “normale”

Quelles que soient les conditions initiales, l’évolution du champ au cours du temps l’amène au minimum de son potentiel. A partir de là, seule l’énergie cinétique du champ peut contribuer à la densité totale et on montre que cette contribution va rapidement devenir négligeable.

4.6.2 “Roulement lent” : [ énergie potentielle très importante + variations temporelles minimes ].

Dans ce cas le champ s’assimile à une constante cosmologique (champ de quintessence ?). Il peut aisément dominer l’Univers. Si le champ domine l’Univers, il le fait entrer dans une phase d’expansion accélérée (inflation) tout en continuant de descendre vers le minimum de son potentiel. Lorsque l’énergie est suffisamment faible, le champ se met à osciller autour de son minimum, ce qui produit des particules et de la radiation au cours d’une phase de réchauffement.

4.6.3 Modèles concurents, modèles mixtes

La phase d’inflation a dû avoir lieu à la température de la grande unification, c’est à dire celle de la transition de phase qui a produit de nombreux défauts topologiques et l’asymétrie des baryons.

L’arrêt de l’inflation est mal compris. Toutes les méthodes aboutissent à un réchauffement de l’Univers. En effet, pour que l’inflation soit efficace, il faut qu’elle est fait grandir l’Univers dans des proportions gigantesques et donc la température à dû chuter de même, au point d’être plus faible que ce que nous mesurons actuellement.

Par ailleurs le champ ne se stabilise pas immédiatement à son potentiel le plus bas mais oscille. Il transforme ainsi son énergie en particules, ce qui freine ses oscillations. Ces dernières particules ont des énergies très importantes. Ensuite elles entrent en collision pour produire une augmentation de la température, éventuellement des défauts topologiques (énergie suffisante) et enfin un équilibre thermique.

Le débat actuel n’est plus entre inflation et défauts topologiques mais entre inflation seule et inflation avec défauts.

4.7 Evènements énergétiques à partir des défauts

Les rayons cosmiques sont des particules élémentaires telles que protons ou électrons accélérés à des vitesses très voisines de celle de la lumière. Le 22 avril 1962 il a été trouvé une énergie de l’ordre de 10²¹ eV.

Un tel niveau implique que la particule est née dans un environnement relativement proche du fait de l’atténuation occasionnée par le fond cosmique. Aucun phénomène conventionnel, ne semble pouvoir expliquer des particules ayant une telle énergie.

Numériquement nous avons :

- énergie reçue ~10²⁰ eV

- accélérateur le plus puissant au monde (LEP) ~10¹² eV

- nouvel accélérateur du CERN (LHC) ~10¹⁵ eV

- échelle de grande unification ~10²⁴ eV

Explications spéculatives par les défauts :

Un défaut topologique formé à une échelle de grande unification contient des particules stables dans le défaut. Si elles sont libérées, elles se désintègrent en un grand nombre de particules de très haute énergie comme des protons.

4.7.1 Monopôles

L’annihilation d’une paire monopôle - antimonopôle, produit des bouffées de particules très énergétiques.

4.7.2 Cordes cosmiques

Un réseau de cordes cosmiques évolue en donnant lieu à l’émission de particules massives très instables (phase de reconnexion).

Série de vues représentant l’évolution d’un segment de corde cosmique au voisinage d’une région de haute courbure.

Tube bleu :

Modélisation de la corde dans une simulation complète de théorie des champs.

Ligne rouge :

Résultat du calcul dans le cas ou la corde se réduirait à une ligne infiniment fine.

Masse grise :

Une partie de la corde s’est annihilée au cours de l’évolution et l’énergie associée est devenue un nuage de rayonnement.

4.7.3 Vortons

Dans certaines conditions de formation, ils peuvent survivre jusqu’à nos jours, remplissant ainsi le rôle de matière noire. Dans ce cas, ce sont les défauts eux-mêmes que l’on va observer dans les rayons cosmiques.

Nous avons vu qu’ils ressemblaient beaucoup à des particules élémentaires aux différences près suivantes:

- Leur charge est ~100 fois plus grande que celle d’un proton. Ils seront donc plus faciles à accélérer dans un champ magnétique.

- Leur masse est aussi plus importante. Leur vitesse sera donc moins importante pour une énergie équivalente.

Puisque le vorton va moins vite que le proton et que sa masse est plus importante, la pression due aux chocs sera moins grande que pour un proton ; il pourra donc parcourir une plus grande distance. En fait il ne devrait pas y avoir de limite (cut-off) comme il y a pour le proton.

5. CONCLUSIONS

5.1 Les observations

Plusieurs expériences sont prévues, qui devraient permettre de vérifier la réalité des différentes hypothèses faites ci-dessus. Ce sont par exemple :

- le projet de satellite Planck de l’ESA, qui sera lancé en 2007 et permettra avec une grande précision de déterminer les paramètres cosmologiques.

- l’observatoire Pierre-Auger qui se consacrera à l’étude des rayons cosmiques de très haute énergie.

- la construction du LHC (Large Hadron Collisionneur), qui devrait permettre dés 2005 d’explorer la zone de quelques dizaines de TeV (10¹⁵ eV).

5.2 Influence sur la réflexion cosmologique

Nous ne pouvons pas faire d’expérience sur l’Univers lui-même. Cependant nous observons des phénomènes pour lesquels il n’y a pas d’explication (formation des structures actuelles, rayons cosmiques de très haute énergie, matière noire), nous devons donc imaginer des mécanismes nouveaux et après études des conséquences, comparer avec les observations. C’est la méthode utilisée ici :

- Les défauts topologiques existent dans de nombreux systèmes physiques.

- Les théories des particules élémentaires en prédisent l’existence en cosmologie.

Existent-ils réellement dans l’Univers ? Espérons que l’avenir proche nous le dira ...

A - 1. L’INFLATION (“principes de la cosmologie” James Rich; éditions école polytechnique)

1.1. Scénario original (Guth) :

Il suppose que l’Univers est piégé dans un vide métastable, dont il échappe par effet tunnel quantique ou par fluctuations thermiques. Ce scénario est étayé par des théories de grande unification.

Cependant, l’effet tunnel équivaut à une transition de phase du premier ordre, et il engendre de grandes inhomogénéités pendant le processus de nucléation. Ce scénario n’est pas en accord avec les observations du fond cosmologique.

1.2. Seconde génération de modèles :

Utilisation de champs scalaires pour créer une énergie du vide effective. Un champs scalaire  caractérisé par un potentiel V(), peut simuler une énergie du vide si les dérivées spatiales et temporelle sont suffisamment faibles. Dans ce cas la densité d’énergie est :  ~ -V().

Lorsque le champ est tombé dans le puits de potentiel, il oscille autour du minimum jusqu’à s’y fixer. Le rayonnement de particules peut être obtenu en couplant  aux champs de matière. Une partie de l’énergie du champ est convertie en énergie de rayonnement (réchauffement).

Un potentiel souvent évoqué à cause de sa simplicité est :

V () =  ⁴, [  est une constante sans dimension et  a la dimension d’une énergie ]

L’équation de Friedmann en unités naturelles est alors : H² = 8   ⁴ / 3 m_pl²

Pour résoudre les problèmes de  et de l’horizon, on a besoin que l’inflation dure pendant N ~ 60 temps de Hubble. On trouve que le champ doit être initialement déplacé de son minimum de la valeur :₂ › N^1/2 m_pl

Il est possible d’avoir une contrainte sur la constante de couplage  en considérant les fluctuations quantiques du champ  (graines à l’origine des structures de l’Univers).

Ces fluctuations sont observées comme étant:   /  ~ 2 x 10^-5 ; elles sont par ailleurs reliées à la pente du potentiel pendant l’inflation :

[   /  ] ~ H³ / V’()

Pour le potentiel  ⁴ et   /  ~ 2 x 10^{-5 ,} cela donne :  ~ (   /  )² / N³ ~ 10^-15

Le champ  est très faiblement couplé à lui-même, ce qui convient pour engendrer les fluctuations de densité observées. Mais la quantique provoque des couplages plus importants qui ne permettent pas de satisfaire les conditions ci-dessus !

- 2. L’INFLATION (“The early Univrers facts and fiction” G. Börner; Springer)

A - 2.1. Pourquoi l’inflation ?

2.1.1. Problème d’horizon

L’homogénéité et l’isotropie observées aujourd’hui impliquent que toutes les régions de l’Univers observable aient été en relation causale à l’origine.

2.1.2. Densité des monopoles

Le modèle GUT entraîne une grande production de monopoles dans l’Univers primordial, qui ne sont pas observés.

A - 2.1. Définition

L’idée s’appuie sur le fait qu’il a pu exister différentes époques ou :3 p +   0

pour ce type de “matière” le facteur d’expansion peut croître plus vite que proportionnellement à t.

Par exemple, quand p +  = 0 , comme pour un champ scalaire doté d’une énergie cinétique négligeable, alors  = cte et pour un modèle ou K = 0 nous obtenons :R(t) = exp { (8G / 3)^1/2  t }

Cette croissance exponentielle de R(t) est appelée “inflation”.

A - 2.2. Quand a-t-elle eut lieu ?

L’idée est de la placer près de la transition de phase de l’époque GUT (un peu après) :

t ~ 10^-35 sec ~ 10⁸ t_pl

A - 2.3. Durée de l’inflation

La période d’inflation se terminera lorsque le facteur d’échelle initial R(t_i) aura été gonflé d’un facteur :

R(t_f) = R(t_i) exp { (8G / 3)^1/2  t } => 10²⁹  Z

L’intervalle de temps t doit être suffisamment long pour que :

^1/2 t ~ 29 ln 10 ~ 70; avec  = (8G / 3) x T_c⁴ ; donc

t ~ ( M_pl x T_c^-2 ) x 70 ~ 10¹¹ t_pl ~ 10^-8 (GeV)^-1;

{ ceci pour T_c = 3 x 10¹⁴ GeV ; t_pl = (1,36)^-1 x 10^-19 GeV et M_pl = 1,36 x 10¹⁹ GeV}.

L’inflation aura débuté aux alentours de 10⁸ t_pl et prendra fin aux alentours de 10¹¹ t_pl. (10^-35 s  10^-32 s )

A - 2.3. Réchauffement

Une inflation par un Z = 10²⁹ , donne une décroissance correspondante de la température : T ~ 10^-15 GeV .

Le couplage entre l’énergie du vide du champ de Higgs et le rayonnement est responsable du réchauffement par la production de particules et de rayonnement. Il est redevenu un Univers de type Friedmann-Lemaître.

A - 2. COMPARAISON ENTRE MODELES et BOOMERANG.

Spectre des fluctuations du rayonnement de fond et données expérimentales.