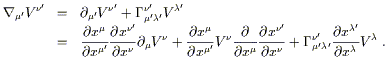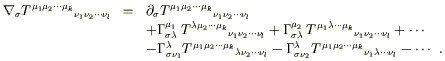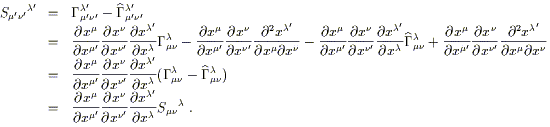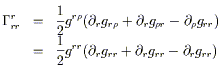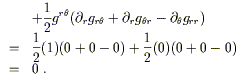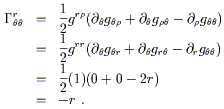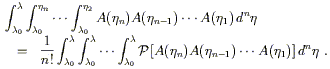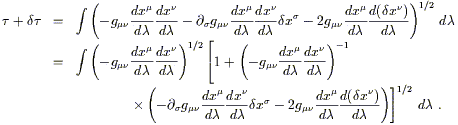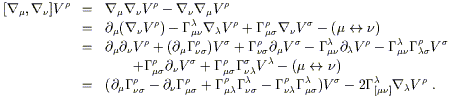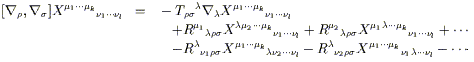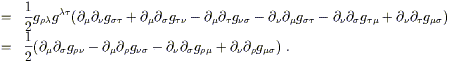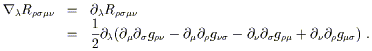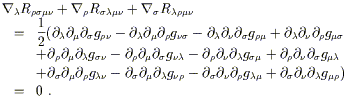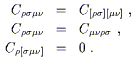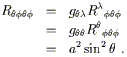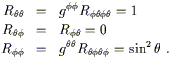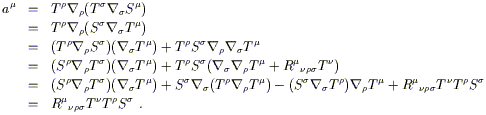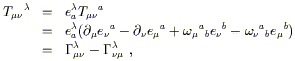lhttp://pancake.uchicago.edu/~carroll/notes/ : J. Fric endosse toute responsabilité pour les erreurs que sa traduction ( qui n'a pas été vérifiée par l'auteur) aurait pu ajouter. En cas de doute, veuillez vous rapporter à la version originale.

3. De la courbure des Espaces (Variétés Riemaniennes)..................................................................... 4

Introduction................................................................................................................................... 4

Connexion métrique...................................................................................................................... 4

Dérivée covariante......................................................................................................................... 4

Propriétés fondamentales........................................................................................................... 4

Coefficients de connexion.............................................................................................................. 5

Propriétés des transformations des dérivées covariantes de Vecteurs.............................................. 5

Les coefficients de connexion ne sont pas des tenseurs................................................................... 6

Dérivée covariante d'un tenseur...................................................................................................... 6

Propriétés complémentaires....................................................................................................... 6

Connexion en Relativité Générale................................................................................................... 8

Le tenseur de torsion..................................................................................................................... 8

Hypothèses complémentaires pour la connexion métrique........................................................... 8

Unicité de la connexion métrique: Sa valeur en fonction de la métrique............................................ 9

Connexion de Christoffel (connexion métrique)............................................................................... 9

Symboles de Christoffel............................................................................................................. 9

Exemple de calcul des symboles de Christoffel......................................................................... 10

Divergence d'un vecteur........................................................................................................... 11

Faisons le point........................................................................................................................... 11

Transport parallèle....................................................................................................................... 12

Transport parallèle d'un vecteur............................................................................................... 12

Le résultat d'un transport parallèle dépend du chemin suivi............................................................ 14

De la difficulté de définir une vitesse relative d'objets éloignés................................................... 14

Définition d'une méthode de transport parallèle......................................................................... 15

Equation du transport parallèle..................................................................................................... 15

Le transport parallèle conserve le produit scalaire de vecteurs................................................... 16

Propagateur parallèle................................................................................................................... 16

Holonomie d'une boucle.......................................................................................................... 18

L'équation géodésique................................................................................................................. 18

L'équation géodésique définie par le vecteur tangent..................................................................... 18

L'équation géodésique défini comme extremum du chemin............................................................ 19

Expression du symbole de Christoffel en fonction du tenseur métrique........................................... 20

Equation géodésique en présence de forces.............................................................................. 20

Paramètres affines................................................................................................................... 21

Conservation type d'intervalle d'espace temps sur une géodésique............................................ 21

"Justification ?" que l'extremum est un maximum........................................................................ 21

De la possible multiplicité des géodésiques............................................................................... 22

Utilisation des géodésiques pour baliser un voisinage : la carte exponentielle.............................. 22

Géodésiques incomplètes......................................................................................................... 23

Théorèmes de singularités........................................................................................................ 23

Le tenseur de courbure de Riemann............................................................................................. 24

Forme générale à priori du tenseur de Riemann........................................................................ 24

Commutateur de dérivées covariantes.......................................................................................... 25

Dans un espace où les composantes du tenseur métrique sont constantes, le tenseur de Riemann est nul et réciproquement................................................................................................................................................... 27

Les (anti)symétries du tenseur de Riemann................................................................................... 29

En quatre dimensions, le tenseur de Riemann a 20 composantes indépendantes......................... 30

L'identité de Bianchi.................................................................................................................... 31

Le tenseur de Ricci :.................................................................................................................... 31

Le scalaire de Ricci..................................................................................................................... 31

Le tenseur d' Einstein................................................................................................................... 32

Le tenseur de Weyl..................................................................................................................... 32

Le tenseur de Weyl est invariant par une transformation conforme............................................. 32

Courbure intrinsèque, courbure extrinsèque.................................................................................. 33

Quelques exemples trompeurs (cylindre, tore).......................................................................... 33

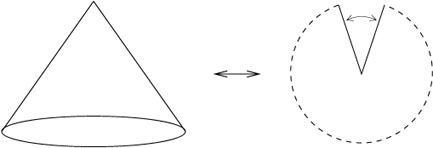
Le cas du cône........................................................................................................................ 34

La courbure de la sphère......................................................................................................... 35

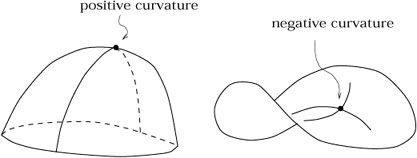
Courbures positives, négatives................................................................................................. 36

La déviation géodésique.............................................................................................................. 37

L'équation de déviation géodésique.............................................................................................. 38

Connexions non métriques........................................................................................................... 38

Base orthonormée de vecteurs non dérivée des fonctions de coordonnées................................ 39

Tétrades, Viebeins....................................................................................................................... 39

Transformations locales de Lorentz (LLT), Transformations générales de coordonnées (GCT).. 41

Connexion de spin....................................................................................................................... 41

Equations de structure de Maurer-Cartan.................................................................................... 43

Dérivée extérieure covariante................................................................................................... 44

Comparaison des connexions et de la courbure en géométrie de Riemann avec celle des théories de jauge en physique des particules.............................................................................................................................. 45

Transformations de jauge, théories de jauge................................................................................. 45

Dérivée covariante de jauge..................................................................................................... 46

Des différences subsistent........................................................................................................ 46

<!DOCTYPE HTML PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN">

3. De la courbure des Espaces ( Variétés Riemaniennes)

Introduction

De notre étude sur les Variétés, il ressort que dès qu'une Variété est définie, nous pouvions immédiatement y définir des fonctions, prendre leurs dérivées, considérer des courbes paramétrées, et y construire des tenseurs entre autres. D'autres concepts comme le volume d'une région, la longueur d'un arc de courbe ont nécessité l'introduction d'une structure fondamentale complémentaire, à savoir : La métrique.

Il vient naturellement à l'esprit, que la courbure d'un espace, concept que nous avons déjà évoqué, dépend de la métrique. En fait, ceci n'est pas suffisamment précis, ou du moins est incomplet.

Connexion métrique

En fait la structure nécessaire que nous devons introduire est la connexion (métrique) qui est caractéristique de la courbure. Nous montrerons comment l'existence d'une métrique implique une certaine connexion (métrique), dont la courbure reflète celle de la métrique.

Cette connexion se révèle nécessaire quand nous voulons remédier au caractère non tensoriel de la dérivée partielle. Nous avons besoin d'une dérivée covariante, opérateur qui se réduit à la dérivée partielle dans les espaces plats, en coordonnées cartésiennes, mais qui respecte la loi de transformation tensorielle dans une variété quelconque. La tradition veut qu'on justifie longuement cette introduction, alors qu'en fait le besoin est évident.

Des équations telles que¶_mT^mⁿ = 0 doivent être généralisées à des espaces courbes d'une certaine manière. Donc nous ne pouvons pas nier que disposer d'une dérivée covariante serait une bonne chose, et regardons comment nous y prendre.

L'opérateur de dérivée partielle (¶_m) dans les espaces plats en coordonnées cartésienne est une application linéaire d'un champ de tenseur (k, l ) vers un autre champ de tenseur (k, l + 1). Il agit linéairement sur les arguments du tenseur et obéit à la règle de Leibniz pour les produits de tenseurs. Tout ceci continue à être vrai dans une situation plus générale, mais le résultat de l'application linéaire dépend du système de coordonnées utilisé.

Dérivée covariante

Nous voudrions définir un opérateur de dérivée covariante qui réaliserait l'opération de dérivée partielle, mais de façon indépendante des coordonnées.

Propriétés fondamentales

Nous exigerons donc de qu'il soit une application linéaire de tenseurs (k, l ) vers des tenseurs (k, l + 1) avec les deux propriétés suivantes:

linéarité: <!-- MATH

$\nabla(T+S) = \nabla T + \nabla S$

-->(T + S) = T + S ;

règle de Leibniz (produit) : (T ÄS) = (T) ÄS + T Ä (S) .

Si obéit à la règle de Leibniz il peut toujours être écrit comme une dérivée partielle plus une transformation linéaire. Pour prendre la dérivée covariante, nous commençons par prendre la dérivée partielle et nous appliquons une correction pour rendre le résultat covariant (nous n'allons pas en faire la preuve, mais vous la trouverez dans "Wald" si cela vous intéresse). Considérons le cas d'un vecteur Vⁿ. Cela signifie que pour chaque direction m, la dérivée covariante Ñ_mva consister en la dérivée partielle ¶_m plus une correction spécifiée par une matrice (G_m)^r_s (une matrice n × n , où n est la dimension de la Variété pour chaque index m).

Coefficients de connexion

En fait les parenthèses sont généralement omises et nous écrirons simplement « G^r_m_s» ces matrices appelées coefficients de connexion. Nous avons donc

<TBODY>

(3.1) </TBODY>

Remarquons que dans le second membre, l'index original du vecteur V a été transféré vers , et le nouvel index ne sert qu'à la sommation. Si c'est bien l'expression de la dérivée covariante d'un vecteur en termes de dérivée partielle, nous devrions être capables de déterminer les propriétés de transformation de Gⁿ_m_l, en exigeant que le membre de gauche soit un tenseur (1,1).

Propriétés des transformations des dérivées covariantes de Vecteurs

Donc, nous voulons que la loi de transformation soit :

<TBODY>

(3.2) </TBODY>

Commençons par le membre de gauche, on peut le développer en utilisant (3.1) et ensuite transformer les parties par les règles que nous connaissons :

<TBODY>

(3.3) </TBODY>

Le membre de droite peut être développé de façon similaire :

<TBODY>

(3.4) </TBODY>

Ces deux expressions doivent être égalées, le premier terme de chaque est identique et s'annule donc, alors nous avons :

<TBODY>

(3.5) </TBODY>

Où nous avons renommé l'index de sommation en. Cette équation doit être vraie pour tout vecteur V^l, donc nous pouvons l'éliminer des deux membres. Ensuite les coefficients de connexion dans les coordonnées "primées" peuvent être isolées en multipliant par x^l/x^l'.

Le résultat est :

<TBODY>

(3.6) </TBODY>

Ce n'est évidemment pas une loi de transformation de tenseur, à cause du second terme.

Les coefficients de connexion ne sont pas des tenseurs

Ceci est normal puisque les coefficients de connexion ne sont pas des tenseurs. Par construction, les 's sont non tensoriels puisqu'ils sont destinés à "corriger" et rendre tensoriels les dérivées partielles qui ne le sont pas, autrement dit annuler le terme qui détruit le caractère tensoriel (donc qui n'est pas un tenseur!) de l'expression (3,1). C'est pourquoi il faut être attentif aux placements des index dans les coefficients de connexion, ils ne sont pas des tenseurs et nous ne pouvons pas les abaisser ou les élever à l'envi.

Dérivée covariante d'un tenseur

Penchons nous maintenant sur le cas des dérivées covariantes des autres types de tenseurs. Par un raisonnement similaire à celui que nous avons utilisé pour les vecteurs, on montre que la dérivée covariante de formes mono linéaires est égale à leur dérivée partielle corrigée par une transformation linéaire. A priori, il n'y a pas de raison que ce soient les même matrices, à base des mêmes coefficients Gⁿ_m_lqui expriment cette transformation. En général nous pouvons écrire :

<TBODY>

(3.7) </TBODY>

où ~Gⁿ_m_l est un nouvel ensemble de matrices pour chaque m. (Attention au placement et à l'utilisation des index). Il est immédiat de montrer que les propriétés de transformation de doivent être les mêmes que , mais à part cela nous n'avons pas d'autres relations.

Propriétés complémentaires

Pour ce faire nous devons introduire deux nouvelles propriétés supplémentaires que nous voudrions que les dérivées covariantes satisfassent :

commutatif vis à vis des contractions: Ñ_m (T^l_l_r) = (T)_m^l_l_r ,
se ramène à une dérivée partielle pour les scalaires : Ñ_mf = ¶_mF.

Ces propriétés ne sont pas dérivées des précédentes, ce sont des exigences nouvelles que nous formulons pour la définition de la dérivée covariante.

Regardons ce qu'elles impliquent. Soit un champ de formes mono linéaires w_m et un champ de vecteurs V^m, nous pouvons prendre la dérivée covariante du scalaire défini par w_l V^l et obtenir

<TBODY>

(3.8) </TBODY>

Mais comme w_l V^l est un scalaire ceci doit se ramener à la dérivée partielle :

<TBODY>

(3.9) </TBODY>

Ceci n'est possible que si les termes comprenant des coefficients de connexion s'annulent dans (3.8) , donc en renommant les indices de sommation nous avons :

<TBODY>

(3.10) </TBODY>

Mais comme w_s et V^l sont arbitraires alors :

<TBODY>

(3.11) </TBODY>

Les deux conditions complémentaires nous ont donc permis d'exprimer la dérivée covariante d'une forme mono linéaire en utilisant les mêmes coefficients de connexion que ceux utilisés pour les vecteurs ( mais en inversant le signe et reliant les index différemment ) :

<TBODY>

(3.12) </TBODY>

Ayons montré que c'était vrai pour les deux types fondamentaux de tenseurs, et compte tenu de la linéarité des opérateurs tensoriels, nous n'allons pas être surpris que les coefficients de connexion contiennent toute l'information nécessaire pour prendre la dérivée covariante de n'importe quel type de tenseur. La formule est biblique, pour chaque index haut , nous devons introduire un terme correctif + , à la dérivée partielle et un terme correctif - pour chaque index bas.

<TBODY>

(3.13) </TBODY>

C'est l'expression générale de la dérivée covariante. Vous pouvez vérifier qu'elle est déduite du jeu d'axiomes que nous avons posé, et des exigences habituelles relatives à l'indépendance du caractère tensoriel vis à vis des coordonnées. Citons une variante de notation utilisant les virgules pour les dérivées partielles et les points virgules pour les dérivées partielles covariantes.

<TBODY>

(3.14) </TBODY>

De nouveau, je rappelle que je ne suis pas adepte de cette notation.

Pour définir la dérivée covariante, nous devons donc munir notre Variété d'une "connexion" qui est spécifié dans un système de coordonnées par l'ensemble de ses coefficients G^l_m_n (n³ = 64 composantes indépendantes pour n = 4 dimensions) qui se transforme selon (3.6). Le nom "connexion" vient du fait qu'elle est utilisée pour transporter des vecteurs d'un espace tangent vers un autre comme nous verrons plus loin. Nous pouvons définir un grand nombre de connexions dans une Variété, chacune associée à une notion différente de dérivée covariante.

Connexion en Relativité Générale

En Relativité Générale, cette liberté ne nous gène pas, car il apparaît qu'à chaque métrique n'est associée qu'une seule connexion. Regardons comment nous y prendre.

La première chose est de remarquer que la différences entre deux connexions est un tenseur (1, 2). Si nous avons deux ensembles de coefficients connexion G^l_m_n et ^G^l_m_n, leur différence S_m_n^l = G^l_m_n - ^G^l_m_n, ( remarquons la position des index) se transforme selon :

<TBODY>

(3.15) </TBODY>

Ce qui est bien conforme à la loi de transformation des tenseurs, donc S_m_n^l est bien un tenseur. Ceci implique que tout ensemble de connexions peut s'exprimer comme la somme d'une connexion irréductible et d'un tenseur quelconque. Remarquons également que d'une connexion donnée, G^l_m_n, on peut immédiatement en former une autre par permutation des index bas. Ceci dit, l'ensemble des coefficients G^l_m_nva se transformer selon (3.6) (car les dérivées partielles présentes dans le dernier terme peuvent être commutées) et ainsi définir une connexion différente.

Le tenseur de torsion

Nous pouvons ainsi associer un tenseur à chaque connexion, appelé le tenseur de torsion, défini par :

<TBODY>

(3.16) </TBODY>

Il est clair que ce tenseur est antisymétrique dans ses indices. Une connexion qui est symétrique dans ses indices est dite sans torsion.

Hypothèses complémentaires pour la connexion métrique

Définissons une connexion unique dans une Variété munie d'une métrique g_m_n en ajoutant deux propriétés:

sans torsion: G^l_m_n= G^l₍_m_n).
Compatibilité métrique : Ñ_rg_m_n = 0.

Définissons la compatibilité métrique d'une connexion (que nous appellerons connexion métrique) par le fait que la dérivée covariante par rapport à la connexion de la métrique soit identiquement nulle. Ceci implique quelques propriétés sympathiques. D'abord, c'est un jeu d'enfant que de montrer que la dérivée covariante de la métrique inverse est également nulle.

<TBODY>

(3.17) </TBODY>

Ensuite, une dérivée covariante compatible avec la métrique est commutative vis à vis de l'abaissement ou de l'élévation d'index. Soit pour un champ de vecteurs V^l,

<TBODY>

(3.18) </TBODY>

Avec des connexions non compatibles avec la métrique il faut être très vigilant sur le placement des index, lorsqu'on exécute une dérivée covariante.

Unicité de la connexion métrique: Sa valeur en fonction de la métrique

Nous revendiquons l'unicité de connexion sans torsion pour une Variété donnée qui est compatible avec une métrique donnée de cette Variété. Nous n'inclurons pas ces deux exigences dans la définition de la dérivée covariante, elles sélectionnent simplement une possibilité parmi de nombreuses. Nous pouvons démontrer et l'existence et l'unicité en dérivant une expression manifestement unique des coefficients de la connexion en termes de la métrique. A cet effet, développons l'équation de compatibilité de la métrique pour les trois permutations différentes des index.

	<TBODY>
		(3.19) </TBODY>

Nous soustrayons la deuxième et la troisième de la première et utilisons la symétrie de la connexion pour obtenir:

<TBODY>

(3.20) </TBODY>

D'évidence, en multipliant par g^s^r , on résout cette équation. Le résultat est :

<TBODY>

(3.21) </TBODY>

C'est une des formules les plus importantes dont on doit se souvenir sur le sujet. Certes nous n'avons fait que prouver qu'il s'il existe une connexion sans torsion et compatible avec la métrique elle doit être de la forme (3.21). Vous pouvez vérifier que le membre de droite de (3.21) se transforme comme une connexion. Cette connexion que nous venons de définir à partir de la métrique est un des piliers de la Relativité générale classique ( gardons toutefois une ouverture d'esprit pour la suite).

Connexion de Christoffel (connexion métrique)

Elle est connue sous différents vocables : Connexion de Christoffel, connexion de Levi-Civita ou connexion de Riemann .

Symboles de Christoffel

Les coefficients de la connexion sont appelés symboles de Christoffel et écrits {^s_m_n} notation que nous éviterons. L'étude des Variétés munis d'une métrique avec leur connexion associée est appelée la Géométrie Riemannienne. L'étude de connexions plus générales a été faite par Cartan, mais nous n'avons jamais entendu parler de la géométrie de Cartan. Avant d'utiliser nos dérivées covariantes, dans ce qui suit, mentionnons quelques unes de leurs propriétés. D'abord rappelons qu'une connexion n'a pas à être construite à partir de la métrique. Dans l'espace plat ordinaire , il y a une connexion implicite que nous utilisons tout le temps, la connexion de Christoffel construite sur une métrique plate. Mais nous pouvons si nous le voulons en choisir une différente, tout en conservant la métrique plate. Remarquons également, que dans une métrique plate, les coefficients de la connexion de Christoffel s'annulent en coordonnées cartésiennes, mais pas en coordonnées curvilignes.

Exemple de calcul des symboles de Christoffel

Considérons par exemple le plan en coordonnées polaires, muni de la métrique :

<TBODY>

(3.22) </TBODY>

Les coefficients non nuls de la métrique inverse sont : g^rr = 1 et g = r^-2. (nous utilisons r et comme index dans cette notation évidente.) Nous pouvons calculer un coefficient de connexion typique :

<TBODY>
		(3.23) </TBODY>

Celui ci s'annule, mais d'autres non :

<TBODY>

(3.24) </TBODY>

Continuons sur notre lancée :

<TBODY>

(3.25) </TBODY>

L'existence de coefficients de connexions non nuls en coordonnées curvilignes est à la source des formules pour la divergence, entre autres, que nous trouvons dans les livres d'électricité et de magnétisme.A contrario, même dans un espace courbe on peut annuler ponctuellement les symboles de Christoffel. Cela s'explique par le fait que nous pouvons annuler les dérivées premières ponctuellement. Ceci n'est bien sûr valable qu'au point, pas dans son voisinage.

Divergence d'un vecteur

Une autre propriété utile est que la formule de la divergence d'un vecteur (conformément à la connexion de Christoffel) prend une forme très simple. La divergence covariante de V^m est donnée par :

<TBODY>

(3.26) </TBODY>

Il est facile de montrer (voir pp. 106-108 de Weinberg) que la connexion de Christoffel satisfait

<TBODY>

(3.27) </TBODY>

Et de là nous obtenons :

<TBODY>

(3.28) </TBODY>

On peut exprimer la divergence de tenseurs de rang plus élevé, mais la formule ne se simplifie pas de cette manière. Un dernier point que nous nous devons de rappeler au sujet des connexions est le fait que la dérivée extérieure est un tenseur parfaitement défini même en l'absence de toute connexion

La raison en est que si on utilise une connexion symétrique (sans torsion), la dérivée extérieure (définie comme dérivée partielle anti-symétrisée) se révèle être égale à la dérivée covariante anti-symétrisée :

<TBODY>

(3.29) </TBODY>

Cela a conduit quelques esprits chagrins à souligner "l'ambiguïté" de la dérivée extérieure dans les espaces avec torsion, ou la simplification ci dessus ne se produit pas. Il n'y a pas d'ambiguïté, la dérivée extérieure se passe de connexion, quelle qu'elle soit et la torsion n'intervient donc pas dans la dérivée extérieure de quoi que ce soit.

Faisons le point

Avant de poursuivre notre œuvre plus avant, récapitulons ce que nous avons fait. Nous partîmes de la notion de base d'un ensemble, supposée connue (au moins informellement). Nous avons introduit le concept de sous ensembles ouverts sur notre ensemble, ce qui est équivalent à introduire une topologie et par la même nous avons promu notre ensemble "espace vectoriel". Ensuite en exigeant que chaque ensemble ouvert soit assimilable à une région de Rⁿ (avec n identique pour chaque ensemble) et aussi que les diagrammes de coordonnées puissent être assemblés sans raccord, l'espace topologique est devenu une Variété. Une Variété est une structure à la fois très souple et très puissante et se trouve munie naturellement d'un faisceau tangent, d'un faisceau de tenseurs quelconques, et de la possibilité de prendre des dérivées extérieures entre autres.

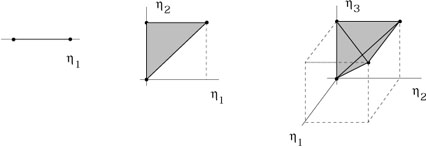
Nous avons ensuite défini une métrique sur la Variété qui est alors devenue une Variété Riemannienne. Indépendamment de la métrique nous avons défini une connexion, nous permettant de prendre des dérivées covariantes. Si nous disposons d'une métrique, nous avons montré qu'il y avait une connexion unique compatible, sans torsion, avec la métrique. Rien ne nous empêche d'ailleurs, de définir d'autres connexions et d'autres métriques sur la Variété. Nous avons résumé tout cela sur le diagramme ci dessous :

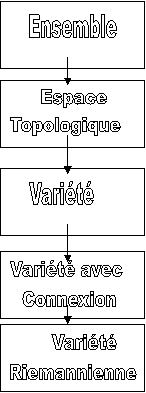
Ensemble, Espace
Topologique,Variété,Variété avec
Connexion, Variété
Riemannienne

Transport parallèle

Transport parallèle d'un vecteur

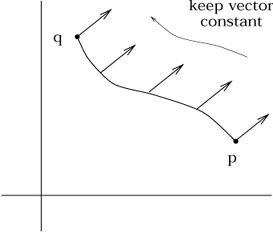
Maintenant que nous disposons du mécanisme de connexion, intéressons nous au transport parallèle. Rappelons qu'en espace plat, il n'était pas nécessaire d'être très attentifs au fait que les vecteurs étaient des éléments d'espaces tangents définis en chaque point. La comparaison (y compris les opérations telles que l'addition, soustraction, produit scalaire .. ) de vecteurs se faisait naturellement en différents points de l'espace. La raison est que dans un espace plat on peut déplacer un vecteur d'un point à un autre en le gardant constant ce qui permet d'effectuer toutes ces opérations autorisées dans un espace vectoriel.

Déplacer un vecteur en le gardant égal à lui même tout au long du chemin s'appelle un transport parallèle. Comme nous allons le voir, le transport parallèle est défini quand nous avons une connexion. La manipulation intuitive des vecteurs dans un espace plat s'appuie sur une connexion de Christoffel implicite dans cet espace.

La différence cruciale entre espace plats et espaces courbes est que dans un espace courbe, le résultat du transport parallèle d'un point vers un autre va dépendre du chemin emprunté pour s'y rendre.

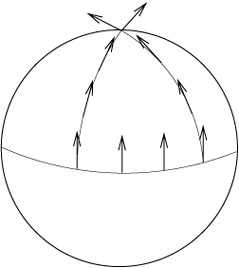
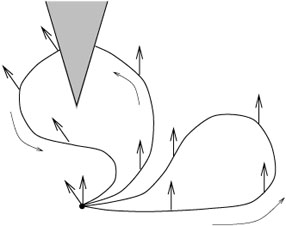
Sans disposer du mécanisme complet du transport parallèle, utilisons notre connaissance de la sphère (2D) pour l'illustrer. Partons avec un vecteur au niveau de l'équateur pointant vers une ligne de longitude constante. Transportons le naturellement jusqu'au pôle nord le long de cette ligne de longitude constante. Repartons du même point avec le même vecteur et transportons le parallèlement le long de l'équateur (pointant vers le nord) d'un angle, puis transportons le vers le pôle nord comme précédemment. On voit clairement sur la figure que le même vecteur transporté par deux chemins différents au pôle nord arrive avec deux positions différentes faisant un angle .

Il apparaît donc qu'il n'y a pas de moyen unique de transporter un vecteur d'un espace tangent vers un autre, nous pouvons toujours le transporter parallèlement, mais le résultat dépend du chemin suivi, et il n'y a pas de choix naturel de chemin à suivre.

Le résultat d'un transport parallèle dépend du chemin suivi

A la différence d'autres problèmes que nous avons rencontré, celui là n'a pas de solution, nous devons admettre que deux vecteurs ne peuvent être comparés naturellement que s'ils appartiennent au même espace tangent.

De la difficulté de définir une vitesse relative d'objets éloignés

Par exemple deux particules se croisant ont une vitesse relative bien définie (inférieure à la vitesse de la lumière). Mais deux particules en deux points différents d'une Variété courbe n'ont pas de vitesse relative bien définie, cette notion de vitesse relative dans ce cas est dépourvue de sens. Certes, dans certaines situations particulières il peut être utile de faire comme si cela en avait un, mais gardons à l'esprit que l'utilité ne se substitue pas à une définition rigoureuse. En Cosmologie par exemple, la lumière provenant de Galaxies lointaines, subit un décalage vers le rouge similaire à celui qui serait produit par le mouvement de récession d'une source proche. Comme ce phénomène ressemble à celui produit par un effet Doppler conventionnel du à une vitesse relative, il est tentant de dire que les Galaxies lointaines s'éloignent de nous à une vitesse définie par leur décalage spectral. D'un point de vue formel, c'est absurde, c'est ce que Wittgenstein appellerait une "faute grammaticale ", on ne peut pas dire que les Galaxies s'éloignent, puisque la notion de leur vitesse par rapport à nous, n'est pas strictement, mathématiquement fondée. Ce qui se passe en fait , c'est que la métrique de l'espace temps entre nous et les Galaxies a changé ( l'Univers s'est étendu) le long du chemin d'un photon entre la bas et ici, produisant un accroissement de la longueur d'onde de la lumière.

Un exemple qui conduit à une explication erronée, est une utilisation naïve de l'effet Doppler qui appliquée sans discernement, nous indiquerait que certaines galaxies s'éloigneraient de nous à une vitesse supérieure à la vitesse de la lumière, en contradiction avec la Relativité. La solution d'un tel paradoxe repose simplement sur le fait que la notion de vitesse relative n'est pas définie correctement.

Maintenant que nous avons vu ce qu'il ne fallait pas faire, regardons ce que nous pouvons faire.

Définition d'une méthode de transport parallèle

Le transport parallèle d'un vecteur est censé être la généralisation dans des Variétés courbes du concept de transport en gardant le vecteur égal à lui même autant que se peut, le long d'un chemin. Ceci vaut aussi pour les tenseurs quelconques.

Soit une courbe x^m (), dans un espace plat, le déplacement d'un tenseur le long de cette courbe, en le maintenant constant ( déplacement parallèle) est caractérisé par dT/dl = (dx^m/dl)(dT/dx^m)= 0. Définissons alors la dérivée covariante sur la courbe par l'opérateur :

<TBODY>

(3.30) </TBODY>

Nous définirons alors le transport parallèle du tenseur T sur le chemin x^m () par le respect tout au long du transport sur le chemin de la condition,

<TBODY>

(3.31) </TBODY>

C'est une équation tensorielle bien définie, car et le vecteur tangent dx^m/d et la dérivée covariante T sont des tenseurs.

Equation du transport parallèle

Cette équation est appelée équation du transport parallèle. Pour un vecteur elle prend la forme

<TBODY>

(3.32) </TBODY>

Nous pouvons considérer l'équation de transport parallèle comme un équation différentielle du premier ordre définissant un problème de valeur initiale. Etant donné un tenseur en un point d'une courbe , il n'y a qu'une seule possibilité de déplacer le tenseur le long de la courbe de telle façon que (3.31). soit satisfait. Nous dirons que nous effectuons un transport parallèle du tenseur. La notion de transport parallèle dépend manifestement de la connexion, et différentes connexions conduisent à différentes solutions. Si la connexion est compatible avec la métrique, la métrique est toujours transportée parallèlement car elle respecte:

<TBODY>

(3.33) </TBODY>

Le transport parallèle conserve le produit scalaire de vecteurs

Il s'ensuit que le produit scalaire de deux vecteurs transportés parallèlement est conservé. Si V^met Wⁿ sont transportés parallèlement sur une courbe x^s (), nous avons :

<TBODY>

(3.34) </TBODY>

Cela signifie que le transport parallèle suivant une connexion compatible avec la métrique conserve la norme des vecteurs, l'orthogonalité entre autres.

Parlons de quelque chose qu'on trouve rarement dans les livres sur la Relativité Générale et qui est l'écriture explicite de la solution générale de l'équation de transport parallèle. Remarquons que pour un chemin g: x^s (), résoudre l'équation de transport parallèle pour un vecteur V^m revient à trouver une matrice P^m_r (,l₀₎ qui relie la valeur initiale du vecteur V^m (l₀) à sa valeur ultérieure en un point du chemin.

<TBODY>

(3.35) </TBODY>

Propagateur parallèle

Evidemment la matrice P^m_r (,l₀₎ appelée le propagateur parallèle dépend du chemin g ( il n'est pas simple de trouver une notation qui l'indique sans faire passer g pour un index. Si nous définissons

<TBODY>

(3.36) </TBODY>

Où la quantité à droite est évaluée à xⁿ (), alors l'équation du transport parallèle devient :

<TBODY>

(3.37) </TBODY>

Et comme le propagateur parallèle doit s'appliquer à n'importe quel vecteur, en reportant (3.35) dans (3.37) on voit que P^m_r (,l₀₎ satisfait à l'équation :

<TBODY>

(3.38) </TBODY>

Intégrons chaque membre pour résoudre l'équation :

<TBODY>

(3.39) </TBODY>

Le symbole de Kronecker delta, est là pour normaliser l'équation pour = l₀.

Nous pouvons résoudre (3.39) par itération, en prenant le membre de droite et en le substituant dans l'expression correspondant au membre de gauche, autant que nécessaire, pour donner :

<TBODY>

(3.40) </TBODY>

Le terme de rang n de cette série est une intégrale sur un triangle rectangle à n dimensions (n-simplex ).

Il serait plus simple de considérer une telle intégrale sur un hyper cube de dimension n au lieu d'un n-simplex, y a t'il un moyen de le faire ? Il y a n! simplex de ce type dans l' hyper cube correspondant, donc nous devons multiplier par 1/n!, pour compenser le volume supplémentaire. Mais nous voulons aussi obtenir l'intégrale correcte, en utilisant la notation matricielle, l'intégrale à l'ordre n est A(h_n)A(h_n-1)^...A(h₁), avec la propriété que h_n ³ h_n-1 ³ …³h₁. Nous allons définir un symbole d'ordonnancement du chemin, , pour s'assurer que la condition est remplie. Autrement dit l'expression:

<TBODY>

(3.41) </TBODY>

Indique que le produit des n matrices A(h_i ), est ordonné de sorte que la valeur la plus grande de h_i est à gauche, et que les valeurs suivantes h_i sont classées dans l'ordre décroissant. Nous pouvons alors exprimer le terme d'ordre n de (3.40) ainsi :

<TBODY>

(3.42) </TBODY>

Cette expression ne contient aucune allusion au sujet des matrices A(h_i ); c'est juste une notation. Nous pouvons écrire (3.40) sous forme matricielle ainsi :

<TBODY>

(3.43) </TBODY>

Cette formule correspond au développement en série d'une exponentielle, nous en déduisons que le propagateur parallèle est défini une exponentielle sur un chemin ordonné.

<TBODY>

(3.44) </TBODY>

Où répétons le, ce n'est qu'une notation, l'exponentielle sur le chemin ordonné est définie comme le membre de droite de (3.43). Nous pouvons donc l'expliciter ainsi :

<TBODY>

(3.45) </TBODY>

Il est agréable de disposer d'une formule explicite, même si elle est un peu abstraite. Le même genre d'expression apparaît dans la théorie quantique des champs (Formule de Dyson), pour la bonne raison que l'opérateur traduisant l'évolution dans le temps de l'équation de Schrödinger a la même forme que celui décrit en (3.38).

Holonomie d'une boucle

Signalons qu'un exemple particulièrement intéressant d'étude du propagateur parallèle est son action sur une boucle (partant et arrivant au même point). S'il s'agit d'une connexion métrique, la matrice résultante va correspondre à une transformation de Lorentz dans l'espace tangent au point en question. Cette transformation est appelée "l'holonomie" de la boucle. Si on connaît l'holonomie de toutes les boucles possibles, cela revient à connaître la métrique. Ceci a conduit Ashtekar et ses collaborateurs à considérer la Relativité générale sous l'angle de la représentation par boucle où les variables fondamentales sont les holonomies en lieu et place de la métrique explicite. Cette approche leur a permis de progresser dans la voie de la quantification de la RG sans pour autant atteindre le but recherché et entrevoir une piste pour cela.

L'équation géodésique

Le transport parallèle maîtrisé, nous pouvons maintenant nous attaquer à l'équation géodésique. Une géodésique est la généralisation aux espaces courbes de la notion de ligne droite de l'espace Euclidien. Nous avons tous ce qu'est une ligne droite, c'est le plus court chemin entre deux points. Nous pouvons en donner une autre tout aussi valable : Une ligne droite est un chemin qui transporte parallèlement son propre vecteur tangent. Dans une Variété munie d'une connexion quelconque (pas nécessairement de Christoffel), ces deux concepts ne coïncident pas, nous les examinerons séparément.

L'équation géodésique définie par le vecteur tangent

Prenons la deuxième définition, en premier, qui se révèle plus simple à calculer. Le vecteur tangent à un chemin x^m () est dx^m/d. La condition de transport parallèle s'exprime par :

<TBODY>

(3.46) </TBODY>

Ou alternativement

<TBODY>

(3.47) </TBODY>

Ceci est l'équation géodésique, une autre formule que nous devons absolument retenir. Elle se ramène à la notion de ligne droite en espace Euclidien si les coefficients de connexion sont ceux de Christoffel, car en coordonnées cartésiennes G^m_r_s= 0, et l'équation devient d²x^m/dl²= 0, ce qui correspond à celle d'une droite. C'est presque trop simple.

L'équation géodésique défini comme extremum du chemin

Examinons maintenant la première définition (distance minimum) Nous avons déjà eu affaire aux subtilités liées à la notion de distance dans un espace temps Lorentzien. Pour les chemins lumière, la distance est nulle, pour les chemins de type temps, le mieux est d'utiliser le temps propre, etc.. Pour simplifier considérons le cas des chemins de type temps, la solution va se révéler exacte pour tous les autres. Considérons la fonction temps propre.

<TBODY>

(3.48) </TBODY>

Où l'intégrale s'applique le long du chemin. Pour rechercher les chemins de longueur minimum, nous allons utiliser le calcul variationnel classique. (En fait l'extremum va se révéler être un maximum). Considérons comment varie le temps propre pour des variations infinitésimales du chemin.

<TBODY>

(3.49) </TBODY>

La deuxième ligne reflète le développement en série de Taylor en espace courbe, qui comme on le voit utilise la dérivée partielle, pas la dérivée covariante. Reportons ceci dans (3.48), nous obtenons :

<TBODY>

(3.50) </TBODY>

Comme x^sest supposé petit, nous pouvons développer la racine carrée de l'expression entre crochets et trouver :

<TBODY>

(3.51) </TBODY>

Il est utile de changer le paramétrage de notre courbe en remplaçant , qui était arbitraire en lui même en utilisant :

<TBODY>

(3.52) </TBODY>

Reportons dans (3.51) (note: nous le reportons pour toutes les occurrences de d), on obtient

<TBODY>
		(3.53) </TBODY>

Où nous avons intégré par parties la dernière ligne, en évitant une contribution aux limites en annulant x^s aux extrémités du chemin. Puisque nous le recherchons pour des points fixes, doit s'annuler quelque soit la variation, ceci implique:

<TBODY>

(3.54) </TBODY>

Où nous avons utilisé dg_m_s/d = (dxⁿ/d)¶_ng_m_s_. Une remise en ordre des index de sommation révèle que :

<TBODY>

(3.55) </TBODY>

Expression du symbole de Christoffel en fonction du tenseur métrique

Et si nous multiplions par la métrique inverse on arrive finalement à :

<TBODY>

(3.56) </TBODY>

Nous voyons que c'est également l'équation géodésique (3.32), mais pour une connexion utilisant spécifiquement les coefficients de Christoffel (3.21). Donc, dans une Variété munie d'une métrique, les extremums de la fonction de longueur sont les courbes qui transportent parallèlement leur vecteur tangent, eu égard à la connexion métrique de Christoffel. Le fait que d'autres connexions puissent être définies sur la même Variété, n'a aucune importance. Evidemment en Relativité Générale nous n'utiliserons que la connexion métrique de Christoffel, ce qui fait que les deux définitions sont équivalentes

L'intérêt principal des géodésiques en Relativité Générale est qu'elles représentent les chemins suivis par les particules non accélérées. En fait l'équation géodésique peut être interprétée comme la généralisation de la loi de Newton= m pour le cas où = 0.

Equation géodésique en présence de forces.

Il est aussi possible d'introduire des forces en ajoutant des termes au membre de droite, en fait si nous faisons un retour en arrière vers l'expression (1.103) exprimant la force de Lorentz en Relativité Restreinte, on peut intuiter que l'équation du mouvement pour une particule de masse m et de charge q en Relativité générale va être quelque chose qui va ressembler à :

<TBODY>

(3.57) </TBODY>

Nous développerons ce point ultérieurement, et confirmerons cette intuition.

Bien qu'ayant développé ces expressions avec une certaine témérité, nous nous devons préciser, tout de même, la notion de paramétrage d'une ligne géodésique.

Paramètres affines

Nous avons paramétré notre chemin par un paramètre , quand nous avons introduit la géodésique en tant que courbe représentant le transport parallèle de son vecteur tangent (3.47), alors que nous avons pris le temps propre comme paramètre lorsque nous avons défini la géodésique comme extremum de d'intervalle d'espace temps (3.56). Ceci mérite une clarification. Une transformation telle que :

<TBODY>

(3.58) </TBODY>

pour des constantes a et b, laisse l'équation invariante. Tout paramètre en relation de ce type avec le temps propre est appelé un paramètre affine et est aussi valide que le temps propre lui même pour caractériser la géodésique. Ce qui est implicite (mais caché) derrière notre formulation de (3.47) est que l'exigence de transport parallèle du vecteur tangent contraint le paramétrage de la courbe à être dépendante du temps propre, tel que défini en (3.58). Autrement dit, si on se place en un point, qu'on pointe dans une direction initiale, et qu'on construit une courbe en commençant par marcher dans cette direction initiale et en conservant le vecteur tangent à la courbe transporté parallèlement, on ne définit pas seulement un chemin dans la Variété, mais aussi (à une transformation linéaire près) un paramètre le long du chemin. Rien n'empêche d'utiliser un autre paramétrage, mais alors (3.47) ne sera plus satisfait. Plus généralement il satisfera une équation de la forme :

<TBODY>

(3.59) </TBODY>

Pour un paramètre et une fonction f (). Inversement, si (3.59) est satisfait le long d'une courbe, il existe un paramètre affine () qui satisfait l'équation géodésique (3.47).

Conservation type d'intervalle d'espace temps sur une géodésique

Une propriété importante des géodésiques dans un espace temps muni d'une métrique Lorentzienne est que le type de l'intervalle d'espace temps (Temps/nul/espace) de la géodésique (dans le cadre d'une connexion métrique) ne change pas. C'est dû au fait que le transport parallèle conserve le produit scalaire et que le type d'intervalle d'espace temps correspond au produit scalaire du vecteur tangent par lui même. C'est pourquoi nous étions fondés à considérer des chemins purement temporels quand nous avons établi (3.56); pour les chemins de type spatial pur nous aurions obtenu le même résultat au signe près. Les géodésiques nulles satisfont aussi la même équation, sauf que le temps propre ne peut pas être utilisé (d'autres paramètres valides existent, liés par des transformations linéaires). On peut établir cela soit à partir de la contrainte de transport parallèle du vecteur, soit en généralisant la variation de (3.48) pour y inclure les chemins de type autre que spatial.

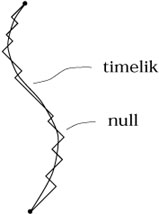
"Justification ?" que l'extremum est un maximum.

Expliquons maintenant pourquoi les géodésiques de type temps maximisent le temps propre. Etant donnée une courbe de type temps (géodésique ou quelconque), nous pouvons essayer de l'approximer, jusqu'à une précision arbitrairement donnée, par une courbe de type nul. A cet effet, nous considérons une ligne brisée constituée de segments de courbes de type nul, encadrant la courbe de type temps comme décrit ci dessous

Si, nous augmentons le nombre de segments, nous allons pouvoir réaliser une meilleure approximation tout en conservant un chemin de type nul. Les géodésiques de type temps ne peuvent donc pas être des courbes qui minimisent le temps propre puisqu'elles peuvent être arbitrairement proches de courbes de temps propre nul, en fait elles maximisent le temps propre.

Rappelez vous le paradoxe de jumeaux, celui qui reste à la maison, reste sur la « géodésique », et subit le temps propre maximum.

De la possible multiplicité des géodésiques

Soulignons ce que ces propos ont de cavalier. Chaque fois que nous disons "maximise" ou "minimise" nous devrions préciser "localement". Il n'est pas rare qu'entre deux points d'une Variété, il y ait plus d'une géodésique.

Par exemple sur S² nous pouvons tracer un grand cercle entre deux points, définissant deux arcs "extremum" entre les deux points mais de longueur manifestement différentes.

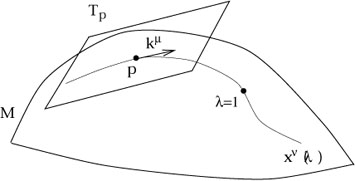
Utilisation des géodésiques pour baliser un voisinage : la carte exponentielle

Un dernier point à souligner, sur les géodésiques avant de passer à la courbure elle même, est leur utilisation pour relier l'espace tangent à un point p au voisinage local de p. Remarquons que toute géodésique x^m () qui passe par p peut être spécifiée par son comportement en p. Choisissons (p) = 0 comme valeur du paramètre et le vecteur tangent en p tel que

<TBODY>

(3.60) </TBODY>

Tel que k^m soit un vecteur en p (un élément de T_p). Alors, il n'y a qu'un point de la Variété M appartenant à cette géodésique correspondant à la valeur = 1. Nous définissons la carte exponentielle à p, exp_p : T_p M, via

<TBODY>

(3.61) </TBODY>

où xⁿ () est solution de l'équation géodésique compte tenu de (3.60).

Pour un ensemble de vecteurs tangents k près du vecteur zéro, cette carte est parfaitement définie et en fait inversible. Donc au voisinage de p, donné par la portée de la carte, pour cet ensemble de vecteurs tangents, les vecteurs tangents eux mêmes définissent un système de coordonnées sur la Variété. Dans ce système de coordonnées, toute géodésique passant par p s'exprime simplement par

<TBODY>

(3.62) </TBODY>

Pour un vecteur k ^mapproprié

Nous ne rentrerons pas dans les détails des propriétés de la carte exponentielle, du fait que nous l'utiliserons peu, mais il est important de souligner que la portée de la carte n'est pas nécessairement la Variété entière et que le domaine n'est pas tout l'espace tangent. La portée peut ne pas être toute la Variété car des points peuvent ne pas être reliés par une géodésique. Dans un espace muni d'une métrique à signature Euclidienne cette restriction est impossible, mais elle est possible dans un espace temps Lorentzien.

Géodésiques incomplètes

Le domaine peut ne pas être tout l'espace tangent T_p car une géodésique peut se terminer sur une singularité qui peut être interprété comme un "bord de la Variété". Les Variétés qui incluent de telles singularités sont dits à géodésique incomplète.

Théorèmes de singularités

Ce n'est pas seulement un problème pour les mathématiciens pointilleux, car les "théorèmes de singularités" de Hawking et Penrose stipulent que sous condition d'un contenu de matière réaliste (pas d'énergie négative), il est pratiquement certain que l'espace temps soit du type géodésiquement incomplet. Par exemple les deux modèles d'espace temps les plus utilisés en Relativité Générale - la solution Schwarzschild décrivant les trous noirs et la solution de Friedmann-Robertson-Walker décrivant les Cosmologies homogènes, isotropes comportent toutes les deux des singularités importantes.

Maintenant que nous avons établi les mécanismes de transport parallèle et les dérivées covariantes, nous sommes prêts pour aborder la courbure proprement dite. La courbure est mesurée par le tenseur de Riemann, qui est lui même construit à partir de connexions. La mesure de la courbure suppose que nous ayons la notion de "platitude" d'une connexion, la connexion conventionnelle ( et habituellement implicite) de Christoffel associée à une métrique Euclidienne ou Minkowski dispose d'un certain nombre de propriétés que l'on peut associer à la platitude. Ceci comprend la propriété de conserver un vecteur, lorsqu'il est transporté le long d'une courbe fermée, que les dérivées covariantes des tenseurs sont commutatives, et que des géodésiques initialement parallèles le restent.

Le tenseur de courbure de Riemann

Le tenseur de Riemann est introduit pour étudier comment ces propriétés sont altérées dans un contexte plus général.

Nous avons déjà montré comment un vecteur transporté parallèlement sur une courbe fermée (boucle) d'une sphère S² était altéré. L'altération dépend de la courbure totale embrassée par la boucle. Il est plus utile d'avoir une description locale de la courbure en tout point, ce que le tenseur de Riemann est censé nous procurer. Une manière classique d'introduire le tenseur de Riemann est d'effectuer un transport parallèle, le long d'une boucle infinitésimale. Nous ne suivrons pas cette voie et irons directement au but. Beaucoup d'ouvrages sont sur ce point soit un peu flottants, soit corrects mais abscons.

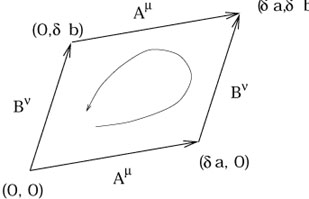
Forme générale à priori du tenseur de Riemann

Néanmoins, sans s'embarrasser des détails, nous pouvons voir la forme que la solution doit prendre. Transportons un vecteur V^s sur une boucle définie par deux Vecteurs A^m et Bⁿ:

Les longueurs infinitésimales des côtés de la boucle sont a et b, respectivement. Comme nous savons que l'action d'un transport parallèle est indépendant des coordonnées, un tenseur doit nous indiquer le changement opéré sur le vecteur par le parcours lorsqu'il revient à son point de départ. Ce doit être une transformation linéaire sur ce vecteur et implique donc un indice et un exposant (pour redonner un vecteur en sortie). Mais il va aussi dépendre des deux vecteurs A et B qui définissent la boucle, donc nous allons trouver deux indices pour opérer sur ces vecteurs A^m et Bⁿ et les contracter. Plus, le tenseur doit être antisymétrique sur ces deux indices, car changer les vecteurs correspond à effectuer le parcours dans l'autre sens, ce qui donne un résultat inverse. Ceci est cohérent avec une transformation à l'identique (modification nulle) si les vecteurs A et B sont identiques. La forme de l'expression traduisant le changement V^r , suite au parcours sur la boucle, se déduit immédiatement.

<TBODY>

(3.63) </TBODY>

où R^r_s_m_n est un tenseur (1, 3) appelé le tenseur de Riemann (ou simplement "tenseur de courbure"). Il est antisymétrique sur ses deux derniers indices.

<TBODY>

(3.64) </TBODY>

Si (3.63) représente la définition de tenseur de Riemann, il faut respecter la convention sur l'ordre des indices, soyons attentifs, car cette convention est arbitraire.

Sachant ce qu'est un transport parallèle, nous pouvons décrire très précisément ce qui arrive au vecteur au cours de cette opération, et le résultat va être une formule fonction des connexions métriques.

Commutateur de dérivées covariantes

Le plus rapide est de considérer une opération connexe, le commutateur (différence entre les permutations) de deux dérivées covariantes. Sa relation avec le transport parallèle le long d'une boucle saute aux yeux, car la dérivée covariante dans une certaine direction mesure le changement du vecteur par rapport à ce qui aurait été s'il avait été transporté parallèlement au même point (rappelons que par définition elle est nulle pour un transport parallèle). Le commutateur de deux dérivées covariantes mesure la différence entre le transport parallèle d'abord dans une direction, puis dans l'autre et l'inverse.

Le calcul est direct. Considérons un champ de vecteurs V^r, nous avons :

<TBODY>

(3.65) </TBODY>

Dans la dernière étape nous avons renommé les indices de sommation et éliminé les termes qui s'éliminent par antisymétrisation. Nous reconnaissons que le dernier terme est simplement le tenseur de torsion et que le membre de gauche est manifestement un tenseur, donc le terme entre parenthèses est un tenseur. Nous écrirons :

<TBODY>

(3.66) </TBODY>

Où le tenseur de Riemann vaut :

<TBODY>

(3.67) </TBODY>

L'établissement de cette expression appelle les remarques suivantes :

Evidemment nous n'avons pas démontré que (3.67) est vraiment le même tenseur que celui défini en (3.63), Mais c'est le même (voir Wald pour une démonstration crédible mais tortueuse).
Il peut paraître surprenant que le commutateur [Ñ_mÑ_n], qui est un opérateur différentiel, agit multiplicativement ( en l'absence de torsion, à n'importe quel niveau) sur un champ de vecteurs. Le tenseur de Riemann contient la mesure de la part qui est proportionnelle au champ de vecteurs dans le commutateur, alors que le tenseur de torsion contient la mesure de la part qui est proportionnelle à la dérivée covariante du champ de vecteurs. A noter l'absence de dérivées secondes.
Remarquons que l'expression de (3.67) est constituée d'éléments non tensoriels, mais nous pouvons vérifier par les lois de transformation que le résultat est un authentique tenseur.
L'antisymétrie de R^r_s_m_n sur ses deux derniers indices est immédiate, au vu de la formule et de son établissement.
Nous avons construit le tenseur de courbure directement à partir de la connexion, sans référence à la métrique. Nous avons pris soin d'établir la formule de façon à ce qu'elle soit valable quelle que soit la connexion ( métrique ou non) indépendamment de la torsion. En utilisant notre technique habituelle nous pouvons généraliser l'action de l'opérateur [Ñ_rÑ_s] sur un tenseur de rang quelconque : Cela donne :

<TBODY>

(3.68) </TBODY>

Une notion utile est le commutateur de deux champs de vecteurs qui est un troisième champ de vecteurs de composantes:

<TBODY>

(3.69) </TBODY>

Le tenseur de Riemann et le tenseur de torsion qui sont tous deux des applications multilinéaires, ont des expressions élégantes en termes de commutateur. Si on considère la torsion comme une application multilinéaire entre deux champs de vecteurs en produisant un troisième nous avons :

<TBODY>

(3.70) </TBODY>

Et si on fait de même pour le tenseur de Riemann , nous avons :

<TBODY>

(3.71) </TBODY>

Dans ces expressions, la notation Ñ_X représente la dérivée covariante le long du champ de vecteur X, de composantes Ñ_X= X^mÑ_m. Remarquons que les vecteurs X et Y dans (3.71) correspondent aux deux indices antisymétriques dans la forme décrivant les composantes du tenseur de Riemann . Le dernier terme de (3.71), relatif au commutateur [X, Y], s'annule quand X et Y forment une base des champs de vecteurs car [¶_m,¶_n] = 0), ce qui explique que ce terme ne soit pas présent dans notre formule originale du commutateur de dérivées covariantes. Nous n'utiliserons pas souvent cette notation, mais vous pourrez être amenés à la rencontrer, autant savoir ce qu'elle signifie. Ayant défini le tenseur de courbure comme un objet qui caractérise la connexion, en Relativité Générale, nous utiliserons essentiellement la connexion métrique (Christoffel). Dans ce cas la connexion dérive directement de la métrique, et la courbure peut à juste titre être interprétée comme celle de la métrique elle même. Cette identification donne un sens à notre notion informelle qui nous fait assimiler les espaces pourvus de métriques de type Euclidien ou Minkowskien à des espaces plats.

Dans un espace où les composantes du tenseur métrique sont constantes, le tenseur de Riemann est nul et réciproquement

En fait, dans un espace où les composantes de la métrique sont constantes, dans un certain système de coordonnées, le tenseur de Riemann est nul, et réciproquement si le tenseur de Riemann est nul, on peut trouver un système de coordonnées où les composantes de la métrique sont constantes.

La première proposition est immédiate, car si dans un système de coordonnées, ¶_sg_m_n = 0 (en tous points), alors G^r_m_n= 0 et ¶_s G^r_m_n = 0; donc R^r_s_m_n = 0 par (3.67). Comme c'est une équation tensorielle, si c'est vrai dans un système de coordonnées, c'est vrai dans tous. Donc la nullité du tenseur de Riemann est une condition nécessaire pour pouvoir trouver un système de coordonnées où les composantes du tenseur métrique g_m_n sont constantes partout. C'est aussi une condition suffisante, bien que ce soit un peu plus difficile de la montrer. Commençons par choisir une système de coordonnées Normales de Riemann au point p, tel que g_m_n = h_m_n en p. (Ici nous utilisons h_m_n dans le sens général d'une matrice diagonale d'éléments +1 où -1 . L'arrangement des +1's et -1's dépend de la forme canonique de la métrique, mais n'apporte rien dans la présente argumentation. Notons les vecteurs de base en p par ê₍_m)_, de composantes ê^s₍_m)_, . Par construction, nous avons :

<TBODY>

(3.72) </TBODY>

Réalisons maintenant un transport parallèle de la base entière de p vers un autre point q, La nullité du tenseur de Riemann nous garantit que ce transport va être indépendant du chemin pris entre p et q. Comme un transport parallèle sur une connexion métrique conserve le produit scalaire, cela implique :

<TBODY>

(3.73) </TBODY>

Nous avons donc défini une base dans laquelle les composantes de la métrique sont constantes. Cela paraît totalement anodin, et peut être réalisé dans n'importe quelle variété, indépendamment de la courbure. Ce que nous voulons montrer est que ceci est une base de coordonnées ( ce qui ne sera vrai que si la courbure est nulle). Nous savons que si les vecteurs ê₍_m) sont une base de coordonnées, leur commutateur s'annule :

<TBODY>

(3.74) </TBODY>

Ce que nous cherchons, c'est la réciproque : Si le commutateur s'annule, nous pouvons trouver des coordonnées y^m telles que ê₍_m)= ¶/¶y^m. Le théorème de Frobenius nous confirme l'exactitude de cette hypothèse. La démonstration est plutôt touffue et faire appel à un arsenal mathématique conséquent, nous l'admettrons donc et les esthètes pourront toujours se rassurer en consultant Schutz's (Geometrical Methods). Malgré tout, nous voudrions démontrer (3.74) pour les champs de vecteurs que nous avons établis. Utilisons (3.70) définissant la torsion:

<TBODY>

(3.75) </TBODY>

La torsion est nulle par hypothèse. La dérivée covariante s'annule aussi, compte tenu de la méthode de construction du champ de vecteurs ( ils résultent d'un transport parallèle sur des chemins arbitraires. Si ces champs ont été transportés sur des chemins quelconques, en particulier ils peuvent être transportés le long des vecteurs ê₍_m)_, , et leurs dérivées covariantes dans cette direction vont être nulles. Alors (3.70) implique que le commutateur s'annule et que par conséquent nous pouvons trouver un système de coordonnées y^m dont ces champs de vecteurs sont les dérivées partielles. Dans ce système de coordonnées la métrique va avoir les composantes h_m_n, comme souhaité.

Les (anti)symétries du tenseur de Riemann

Le tenseur de Riemann, du fait de ses 4 index a n⁴ composantes dans un espace à n-dimensions L'antisymétrie du tenseur (3.64) réduit à n(n - 1)/2 le nombre de composantes indépendantes sur les deux derniers index et nous laisse n³(n - 1)/2 composantes indépendantes. Si nous considérons une connexion de Christoffel, nous trouvons d'autres symétries qui réduisent encore ce nombre de composantes indépendantes. Intéressons nous à cela :

Construisons le tenseur de Riemann avec tous les index bas :

<TBODY>

(3.76) </TBODY>

Considérons les composantes de ce tenseur en Coordonnées Normales de Riemann au point p. Alors les symboles de Christoffel vont s'annuler , bien que leur dérivées ne s'annulent pas.

Nous avons donc

	<TBODY>
		(3.77) </TBODY>

Dans la seconde ligne nous avons utilisé le fait que ¶_mg^l^t = 0 en Coordonnées Normales de Riemann et dans la troisième ligne le fait que les dérivées partielles commutent. De cette expression, nous remarquons immédiatement deux propriétés de R_r_s_m_n. Il est antisymétrique dans ses deux premiers indices ,

<TBODY>

(3.78) </TBODY>

Et il est invariant par l'échange de la première paire d'indices avec la seconde.

<TBODY>

(3.79) </TBODY>

En poursuivant l'étude ( ce que nous vous laissons le soin de faire) nous mettrions en évidence que la somme de des permutations cycliques sur les trois derniers indices est nulle.

<TBODY>

(3.80) </TBODY>

Cette dernière propriété peut s'énoncer comme la nullité de la partie antisymétrique sur les trois derniers indices, soit :

<TBODY>

(3.81) </TBODY>

Toutes ces propriétés ont été établies dans un système de coordonnées particulier, mais s'agissant d'équations tensorielles, si elles sont valables dans un système de coordonnées, elles le sont dans tous.

Ces propriétés ne sont pas toutes indépendantes, et moyennant un petit effort, on peut trouver que (3.64), (3.78) et (3.81) ensembles impliquent (3.79). L'interdépendance logique ne doit pas nous troubler outre mesure, l'important est l'existence de ces propriétés.

Compte tenu de toutes ces relations entre les composantes, combien en reste t'il d'indépendantes?

Commençons par l'antisymétrie de R_r_s_m_nsur ses deux premiers indices, sur ses deux derniers indices, et la symétrie entre ces paires. Nous pouvons nous représenter cela par une matrice symétrique R_[_r_s_][_m_n_], où les paires rs et mn jouent le rôle d'index. Une matrice symétrique m × m a m(m + 1)/2 composantes indépendantes alors qu'une matrice n × n antisymétrique a n(n - 1)/2 composantes indépendantes. Il s'ensuit que le nombre de composantes indépendantes est :

<TBODY>

(3.82) </TBODY>

Nous n'avons pas encore tenu compte de (3.81). L'effet immédiat de (3.81) est que la totalité de la partie antisymétrique du tenseur de Riemann s'annule :

<TBODY>

(3.83) </TBODY>

En fait, cette équation, plus les autres symétries (3.64), (3.78) et (3.79) impliquent (3.81), ce qui peut être montré facilement en développant (3.83) et en réarrangeant les termes résultants. Donc (3.83) est équivalent à appliquer (3.81), quand les autres symétries ont été appliquées. Combien de contraintes complémentaires résultent de cette relation ? Décomposons comme suit :

<TBODY>

(3.84) </TBODY>

Il est facile de voir que tout tenseur à 4 index entièrement antisymétrique est bien sur antisymétrique entre ses premiers et derniers indices, et symétrique par échange des deux paires. Donc ces propriétés sont des contraintes indépendantes liées à (3.83), de X_r_s_m_n, de celles déjà prises en compte.

Un tenseur totalement antisymétrique à 4 index a n(n - 1)(n - 2)(n - 3)/4! Termes indépendants, et donc (3.83) réduit le nombre de composantes indépendantes par cette valeur. Il nous reste :

<TBODY>

(3.85) </TBODY>

Composantes indépendantes du tenseur de Riemann.

En quatre dimensions , le tenseur de Riemann a 20 composantes indépendantes

En quatre dimensions , le tenseur de Riemann a 20 composantes indépendantes. (En une dimension, il n'en a aucune). Ces vingt fonctions correspondent précisément aux vingt degrés de liberté des dérivées secondes de la métrique que nous n'avions pas pu annuler par un changement de coordonnées. Cela devrait nous conforter dans le choix de ce tenseur pour représenter la courbure de l'espace. En plus des symétries algébriques du tenseur de Riemann, qui contraignent le nombre de composantes indépendantes en chaque point, il obéit à une identité différentielle qui contraint ses valeurs relatives en différents points. Considérons la dérivée covariante du tenseur de Riemann évalué en Coordonnées Normales Riemanniennes :

<TBODY>

(3.86) </TBODY>

Considérons les permutations cycliques sur les trois premiers indices.

<TBODY>

(3.87) </TBODY>

L'identité de Bianchi

Comme c'est une équation tensorielle elle est vraie dans n'importe quel référentiel. Nous voyons que l'antisymétrie R_r_s_m_{n =
-}R_s_r_m_{n ,}nous permet d'écrire ce résultat sous la forme :

<TBODY>

(3.88) </TBODY>

Ceci est appelé l'identité de Bianchi . (Remarquons que pour une connexion quelconque nous aurions des termes supplémentaires relatifs au tenseur de torsion.. Elle est en relation étroite avec l'identité de Jacobi (vous pouvez le démontrer) car au fond, elle exprime que

<TBODY>

(3.89) </TBODY>

Le tenseur de Ricci :

Il est souvent utile de considérer les contractions du tenseur de Riemann. Même sans métrique , nous pouvons le contracter pour donner le tenseur de Ricci :

<TBODY>

(3.90) </TBODY>

Remarquons que pour un tenseur de courbure formé à partir de connexions quelconques (pas forcément de Christoffel), il y a plusieurs contractions possibles. Notre intérêt principal portant sur la connexion métrique (Christoffel), nous voyons que (3.90) est la seule contraction indépendante possible, à la convention de signe près. Le tenseur de Ricci associé à une connexion métrique est symétrique, du fait des symétries du tenseur de Riemann.

<TBODY>

(3.91) </TBODY>

Le scalaire de Ricci

En utilisant la métrique nous pouvons opérer une contraction complémentaire pour produire le scalaire de Ricci.:

<TBODY>

(3.92) </TBODY>

Une forme particulièrement utile de l'identité de Bianchi est obtenue à partir de (3.87) en la contractant deux fois.

<TBODY>

(3.93) </TBODY>

soit

<TBODY>

(3.94) </TBODY>

Le tenseur d' Einstein

A l'inverse de la dérivée partielle, il est parfaitement légal d'élever un index sur la dérivée covariante, du fait de la compatibilité métrique. Si nous définissons le tenseur d' Einstein par :

<TBODY>

(3.95) </TBODY>

Nous voyons que l'identité de Bianchi deux fois contractée (3.94) est équivalente à :

<TBODY>

(3.96) </TBODY>

Le tenseur d'Einstein qui symétrique du fait de la symétrie du tenseur de Ricci et de la métrique est de la plus haute importance en Relativité générale.

Le tenseur de Ricci et le scalaire de Ricci contiennent de l'information sur les "traces" du tenseur de Riemann.

Le tenseur de Weyl

Il est parfois utile de considérer séparément les morceaux du tenseur de Riemann non décrit par le tenseur de Ricci. C'est le tenseur de Weyl , qui est construit à partir du tenseur de Riemann en lui retirant toutes ses contractions. Il s'exprime en n dimensions par

<TBODY>

(3.97) </TBODY>

Cette formule alambiquée est conçue de sorte que toutes les contractions possibles de C_r_s_m_ns'annulent, tout en retenant toutes les symétries du tenseur de Riemann:

<TBODY>

(3.98) </TBODY>

Le tenseur de Weyl n'est défini qu'à partir (et au delà ) de 3 dimensions, et en trois dimensions , il est nul. Pour n ³ 4, il satisfait une version de l'identité de Bianchi.

<TBODY>

(3.99) </TBODY>

Le tenseur de Weyl est invariant par une transformation conforme

Une des propriétés les plus importantes du tenseur de Weyl est qu'il est invariant par une transformation conforme. Ceci signifie que si on calcule C_r_s_m_npour une métrique g_m_n, et qu'on le calcule de nouveau pour une métrique donnée par W² (x) g_m_n, , où (x) est une fonction non nulle de l'espace temps, on obtient la même chose. Pour cet raison, il est souvent appelé le "tenseur conforme".

Après ce déluge de formalisme, il est temps de souffler et de regarder ce que la courbure signifie et représente sur des exemples simples. Rappelons que d'après (3.85), en 1, 2, 3 et 4 dimensions il y a respectivement 0, 1, 6 et 20 composantes indépendantes pour le tenseur de courbure. Tout ce que nous dirons dans ces exemples supposera que la courbure est définie sur une connexion métrique. Cela signifie que les Variétés unidimensionnelles ( telles que S¹) ne sont jamais courbées. L'idée que nous avons de la courbure d'un cercle vient que nous le pensons inclus dans plan bidimensionnel. Il y a une notion de courbure extrinsèque qui caractérise la manière dont quelque chose est inclus dans un espace de dimensions supérieures. Nous nous référons à la courbure intrinsèque qui n'a rien à voir avec de telles inclusions.

Courbure intrinsèque, courbure extrinsèque

La distinction entre courbure intrinsèque et extrinsèque est également importante en deux dimensions., où la courbure a une composante indépendante ( En fait toute l'information de courbure est contenue dans l'unique composante du scalaire de Ricci).

Quelques exemples trompeurs ( cylindre, tore)

Considérons un cylindre × S¹.

Bien que de notre point vue, il nous paraisse courbe, il est pourtant clair que nous pouvons définir une métrique sur le cylindre dont les composantes sont constantes dans un système de cordonnées approprié, en simplement le déroulant et utilisant la métrique du plan. Dans cette métrique le cylindre est plat. On pourrait introduire d'autres métriques où le cylindre ne serait pas plat, mais le point que nous voulons souligner est que cette métrique peut être rendue plate. Même scénario pour le tore.

Nous pouvons construire un tore (S¹ × S¹) à partir d'un carré en joignant et collant les côtés opposés comme indiqué sur la figure. De nouveau nous reconnaissons une métrique plate, bien que du point de vue extrinsèque, il apparaisse de plus en plus courbe.

Le cas du cône

Un cône est un exemple de Variété à deux dimensions avec une courbure non nulle en un seul point. Ceci se voit si on déroule le cône, il est alors équivalent à un plan amputé d'un angle formé par les côtés opposés identifiés ( angle de déficit).

De la métrique résultant de cette définition, on voit que la cône est plat partout sauf au sommet. Ceci peut être visualisé en transportant parallèlement un vecteur sur diverses boucles. Si la boucle n'inclut pas le sommet, le vecteur est inchangé, si la boucle inclut le sommet ( disons une fois), alors le vecteur subit une rotation d'un angle égal à l'angle de déficit.

La courbure de la sphère

Un exemple, que nous chérissons particulièrement, est celui de la sphère S² munie de la métrique

<TBODY>

(3.100) </TBODY>

où a est le rayon de la sphère (imaginé représenté dans R³ ). Sans entrer dans les détails, les coefficients de la connexion non nuls sont :

<TBODY>

(3.101) </TBODY>

Calculons une composante intéressante du tenseur de Riemann :

	<TBODY>
		(3.102) </TBODY>

(La notation est un peu confuse, car la lettre grecque est un index de sommation alors que les lettres grecques et Freprésentent des coordonnées spécifiques. En abaissant les index nous avons :

<TBODY>

(3.103) </TBODY>

C'est un jeu d'enfant de vérifier que tous les autres composantes de tenseur de Riemann sont nulles ou égale à celle là par symétrie.

Continuons en calculant le tenseur de Ricci via R_m_n = g^a^bR_a_m_b_n, nous obtenons :

<TBODY>

(3.104) </TBODY>

Le scalaire de Ricci s'obtient aussi directement :

<TBODY>

(3.105) </TBODY>

Donc, sur une variété à deux dimensions, le scalaire de Ricci caractérise complètement la courbure qui est constante sur une sphère S². Ceci reflète la propriété de "symétrie maximum" sur une Variété, notion que nous développerons ultérieurement, même cela vous paraît à juste titre évident. Dans un espace de dimension quelconque, la courbure de l'espace à symétrie maximum satisfait ( pour une constante a)

<TBODY>

(3.106) </TBODY>

Qui est vérifié par cet exemple, comme de bien entendu.

Remarquons que le scalaire de Ricci est constant pour la sphère et est de plus positif. Nous dirons que la sphère possède comme le scalaire de Ricci, une courbure positive (nonobstant des conventions diverses qui au moins convergent sur ce point). Du point de vue d'un observateur vivant dans la Variété, incluse dans un espace Euclidien de dimensions supérieures, s'il est assis en un point d'un espace à courbure positive, il voit l'espace s'incurver de la même façon dans toutes les directions, alors qu'assis en un point d'un espace à courbure négative il le voit s'incurver de façon opposée dans les différentes directions.

Courbures positives, négatives

Les espaces 2D à courbure négative ressemblent à des selles de cheval (sans le cheval, bien entendu).

Assez ri avec les exemples. Nous avons encore un sujet à traiter avant d'introduire la relativité générale, la déviation géodésique.

La déviation géodésique

Vous savez sans doute que la géométrie Euclidienne s'appuie sur le postulat des parallèles qui ne se rencontrent jamais. Dans un espace courbe, ceci n'est plus vrai, sur une sphère, des géodésiques parallèles en un point peuvent se couper. Nous nous devons de quantifier cette propriété dans un espace courbe arbitraire.

Premier problème, la notion de parallèle ne se généralise pas naturellement d'un espace plat à un espace courbe. Nous allons donc construire une famille de géodésique à un paramètre g_s (t). Pour chaque s Î, g_s est une géodésique paramétrée par le paramètre affine t. L'ensemble de toutes ces courbes définit une surface continue à deux dimensions ( inclus dans une Variété M de dimension supérieure quelconque). On peut choisir s et t, comme coordonnées pourvu que nous ayons choisi une famille de géodésiques qui ne se coupent pas. La surface entière est alors l'ensemble des points x^m (s, t) Î M. Nous avons deux champs de vecteurs naturels : les vecteurs tangents aux géodésiques.

<TBODY>

(3.107) </TBODY>

Et les vecteurs de "déviation "

<TBODY>

(3.108) </TBODY>

Cela vient de la notion informelle que S^m pointe d'une géodésique vers ses voisines.

L'idée que S^m pointe d'une géodésique vers la suivante suggère de définir la "vitesse relative des géodésiques".

<TBODY>

(3.109) </TBODY>

et " l'accélération relative des géodésiques,"

<TBODY>

(3.110) </TBODY>

Pour les noms, ça se discute, mais ce qui est sûr c'est que ces vecteurs existent bien. Comme S et T sont les vecteurs de base du système de coordonnées, le commutateur s'annule.

[S, T] = 0.

Considérons le cas standard ou la torsion est nulle, alors de (3.70) nous tirons :

<TBODY>

(3.111) </TBODY>

Tenant compte de cela, calculons l'accélération:

<TBODY>

(3.112) </TBODY>

Examinons cette expression ligne par ligne. La première ligne est la définition de a, et la seconde ligne résulte de l'application de (3.111). L'application de la règle de Leibniz donne la troisième ligne. La quatrième ligne est obtenue en remplaçant la double dérivée covariante par les dérivées en sens contraires plus le tenseur de Riemann. La règle de Leibniz est de nouveau utilisée pour produire la cinquième ligne (dans l'ordre inverse à celui habituel), et nous éliminons deux termes identiques et remarquons que le terme invoquant T^rÑ_r T^m s'annule car T^m est un vecteur tangent à une géodésique. Il vient :

L'équation de déviation géodésique

<TBODY>

(3.113) </TBODY>

Cette formule est appelée l'équation de déviation géodésique Elle exprime quelque chose qui était prévisible : l'accélération relative entre deux géodésiques est proportionnelle à la courbure.

D'un point de vue physique , l'accélération entre géodésique voisines est interprétée comme la manifestation des forces de marée. Cela nous rapproche de la physique.

Connexions non métriques

Le dernier aspect formel à traiter avant de nous intéresser à la gravitation concerne le formalisme précis des connexions et de la courbure. Cette fois nous allons utiliser un ensemble de vecteurs de bases de l'espace tangent qui n'est pas dérivé d'un quelconque système de coordonnées.

Il apparaît que cette nuance, dans l'approche, nous révèle un autre aspect de la connexion et de la courbure, où les relations avec les théories de jauge de la physique de particules sont plus claires. Les concepts que nous introduisons sont plutôt immédiats, mais la notation est cauchemardesque, ce qui fait apparaître la chose plus complexe qu'elle n'est.

Jusqu'à présent nous avons tenu compte du fait qu'une base naturelle de l'espace tangent T_p à un point p est donné par les dérivées partielles respectivement aux coordonnées en ce point ê₍_m) = ¶_m. Itou pour l'espace cotangent T^*_p où la base est donnée par les gradients des fonctions de ds coordonnées, = dx^m. Rien ne nous interdit de prendre une autre base. Supposons qu'en chaque point de la Variété nous introduisons un ensemble de vecteurs de base ê₍_a) (indexé par une lettre latine plutôt que grecque pour nous rappeler que nous ne faisons pas référence à un système de coordonnées).

Base orthonormée de vecteurs non dérivée des fonctions de coordonnées

Nous choisirons ces vecteurs orthonormés, au sens approprié à la signature de la Variété que nous considérons. Si la forme canonique de la métrique est écrite h_ab, nous imposons au produit scalaire des vecteurs de base la condition :

<TBODY>

(3.114) </TBODY>

Où g( , ) est le tenseur métrique habituel. Alors dans un espace Lorentzien h_ab, représente la métrique de Minkowski, tandis qu'une signature définie positive représentera une métrique d'espace Euclidien.

Tétrades, Vielbeins

L'ensemble des vecteurs constituant une base orthonormée est quelquefois appelée une tétrade (grec), (vielbeins en allemand). Dans des espaces de dimensions différentes ils sont selon la circonstance appelés triade (3), … etc. Comme nous ne pouvons pas en général couvrir la variété avec un seul diagramme de coordonnées, nous ne pourrons pas trouver un ensemble de vecteurs de bases définis partout. Nous procéderons comme d'habitude par morceaux d'espaces et opérerons leur recollement sans raccord en normalisant les recouvrements par une application bijective;

Etant donné cette base, un vecteur quelconque peut s'exprimer par une combinaison linéaire des vecteurs de bases. En particulier nous pouvons exprimer nos anciens vecteurs de base ê₍_m) = ¶_m en fonction des nouveaux :

<TBODY>

(3.115) </TBODY>

Les composantes de e^a_m forment une matrice n × n inversible. (Conformément à notre habitude de confondre les objets et leurs composantes, nous nous réfèrerons à e^a_m en tant que tétrade, et souvent au pluriel à "tétrades."). L'inverse sera noté, en inversant les index e^m_a, il satisfait

<TBODY>

(3.116) </TBODY>

Elles sont les composantes des vecteurs ê₍_a) dans la base de coordonnées.:

<TBODY>

(3.117) </TBODY>

Exprimé en termes d'inverse des tétrades, (3.114) devient

<TBODY>

(3.118) </TBODY>

Soit également

<TBODY>

(3.119) </TBODY>

La dernière équation fait dire à certains que les tétrades sont les racines carrées de la métrique

Nous pouvons faire de même pour établir une base orthonormée pour les formes monolinéaires dans T^*_p, que nous noterons . Nous pouvons les choisir de façon à ce qu'ils soient compatibles avec la base de vecteurs dans le sens où

<TBODY>

(3.120) </TBODY>

Comme conséquence immédiate de ceci, les formes mono linéaires orthonormées sont liées à leurs cousins = dx^m définis dans la base de coordonnées par

<TBODY>

(3.121) </TBODY>

<TBODY>

(3.122) </TBODY>

Les tétrades e^a_m ont alors un double usage : composantes des vecteurs de la base de coordonnées dans la base orthonormée et composantes des vecteurs de la base orthonormée de formes monolinéaires dans la base de coordonnées des formes mono linéaires, tandis que l'inverse des tétrades sont les composantes des vecteurs de la base orthonormée dans la base de coordonnées et les composantes de la base de coordonnées des formes mono linéaires dans la base orthonormée. Tout autre vecteur peut s'exprimer par ses composantes dans la base orthonormée. Si un vecteur V s'écrit V^m ê(_m) dans la base de coordonnées et V^a ê(_a)dans la base orthonormée , les ensembles de composantes satisfont à :

<TBODY>

(3.123) </TBODY>

Donc les Tétrades nous permettent de passer des indices latins aux grecs et vice versa. La propriété sympathique des tenseurs, qui est que compte tenu du placement des index, il n'y a qu'une chose à peu près sensée que l'on puisse faire nous est d'un grand secours ici. Nous pouvons donc enchaîner et appliquer cela à des tenseurs sur leurs multiples index même mixtes.

<TBODY>

(3.124) </TBODY>

Retournant à (3.118), nous voyons que les composantes du tenseur métrique dans la base orthonormée sont précisément celles d'une métrique plate, h_ab (pour cette raison on qualifie souvent les index grecs de courbe et les index latins de plat). En fait rien ne nous empêche d'élever ou abaisser les index latins en utilisant la métrique plate et son inverse h^ab . Vous pouvez vérifier que cela donne des résultats parfaitement corrects (abaisser un index avec la métrique fait passer d'une base orthonormée à une base de coordonnées). En particulier, notre définition des térades inverses est cohérente avec notre notion habituelle d’élévation et d’abaissement d’indices.

e^µ_a = g^μνη_abe_ν^b (3.124-bis)

Nous avons introduit les tétrades e_ν^a comme composantes d’un ensemble de vecteurs de bases, évalués dans une base différente. Ceci est revient à les considérer comme les composantes d’un tenseur (1,1).

e = e_ν^adx^ν ^ ê₍_a) (3.124 ter)

Un tenseur que nous connaissons et apprécions est le tenseur « identité ». En appliquant ce tenseur sur un vecteur, nous obtenons le même vecteur, dans une base différente. C’est ce que montre (3.123). De même, si nous utilisons la tétrade inverse pour convertir un index latin de e^ν_a, en un index grec, conformément à (3.116), nous obtenons δ^μ_ν qui est l’application identité sur les vecteurs et 1-formes. Ce point mérite d’être souligné, car nous pourrions choisir d’interpréter e_ν^a comme un ensemble de composantes d’un vecteur (certains ouvrages le font), au quel cas la dérivée covariante paraîtrait différente.

En introduisant un nouvel ensemble de vecteurs de bases et de formes mono linéaires, nous devons retourner à notre sujet favori, les propriétés de transformation. Nous avons toujours prudemment déclaré que la loi de transformation des tenseurs n'était qu'une conséquence indirecte des transformations de coordonnées. Maintenant, nous avons une base non définie à partir des coordonnées et cette base peut être changée indépendamment des coordonnées, la seule contrainte (3.114) étant qu'elles soient et restent orthonormées. Mais nous savons quelles transformations conservent la métrique plate, dans une métrique Euclidienne à signature positive ce sont les transformations orthogonales, tandis que dans une métrique à signature Lorentzienne, ce sont les transformations de Lorentz. Nous considérons donc des changements de base de la forme :

<TBODY>

(3.125) </TBODY>

Où les matrices L_a'^a(x) représentent des transformations dépendantes de la position qui en chaque point conservent la forme canonique de la métrique.

<TBODY>

(3.126) </TBODY>

En fait ces matrices correspondent à ce que nous avons appelé en espace plats la transformation inverse de Lorentz (qui opère sur les vecteurs de base), comme avant nous avons aussi les transformations de Lorentz normales L^a'_a, qui transforment une base de formes mono linéaires. En termes de composantes, comme avant les index hauts sont transformés par L^a'_a et les index bas sont transformés par L_a'^a .

Transformations locales de Lorentz ( LLT), Transformations générales de coordonnées (GCT)

Nous avons donc la possibilité de réaliser une transformation de Lorentz (où une simple rotation Euclidienne selon la signature) en chaque point de l'espace. Ces transformations sont appelées en conséquence transformations locales de Lorentz (LLT). Nous pouvons toujours changer de coordonnées, par des transformations générales de coordonnées (GCT). Nous pouvons combiner ces deux opérations, le résultat étant un tenseur mixte pour la loi de transformation.

<TBODY>

(3.127) </TBODY>

Transposer notre connaissance sur les tenseurs dans des bases qui ne sont pas celles de coordonnées, est principalement un exercice de manipulation de tétrades, en respectant scrupuleusement les emplacements. L'exception cruciale concerne la différentiation. Dans notre formalisme habituel, la dérivée covariante d'un tenseur est formée de la dérivée partielle et de termes correctifs, un pour chaque index invoquant le tenseur et les coefficients de connexion.

Connexion de spin

La même procédure va s'appliquer pour des bases différentes de celles de coordonnées, mais en remplaçant les coefficients de connexion habituels G^l_m_n par une connexion de spin notée w_m^a_b. Chaque index latin correspond à au facteur de connexion de spin comme d'habitude.

<TBODY>

(3.128) </TBODY>

(Le nom "connexion de spin" vient de ce qu'elles sont utilisées pour prendre les dérivées covariantes des spinneurs, ce qui n'est pas possible avec les coefficients de connexion habituels).

En présence d'une combinaison de lettres latines et grecques, nous avons des termes correctifs des deux types.

La contrainte d'indépendance d'un tenseur vis à vis de sa représentation, nous permet de dériver des relations entre la connexion de spin, les tétrades et les Gⁿ_m_l . Considérons la dérivée covariante d'un vecteur X, d'abord dans une base de coordonnées.

<TBODY>

(3.129) </TBODY>

Maintenant intéressons nous au même objet dans une base mixte et convertissons le dans la base de coordonnées.

<TBODY>

(3.130) </TBODY>

La comparaison avec (3.129) révèle :

<TBODY>

(3.131) </TBODY>

Soit :

<TBODY>

(3.132) </TBODY>

En triturant quelque peu l'expression, nous pouvons l'écrire sous forme d'annulation de la dérivée covariante de la tétrade,

<TBODY>

(3.133) </TBODY>

Ceci est quelquefois appelé le "postulat des tétrades". Remarquons que ceci est toujours vrai, pas besoin de la moindre hypothèse sur la connexion pour l'établir. En particulier la connexion n'a pas besoin d'être métrique et sans torsion.

Comme le connexion peut être interprétée comme quelque chose de nécessaire pour rendre la loi de transformation de la dérivée covariante, il n'est pas surprenant que la connexion de spin n'obéisse pas à la loi de transformation des tenseurs. De fait, l'index bas grec se transforme correctement en forme mono linéaire par la transformation générale de coordonnées (GCT).

Mais la connexion de spin se transforme de façon non homogène par la transformation locale de Lorentz (LLT ) selon

<TBODY>

(3.134) </TBODY>

Nous vous invitons à vérifier que cela résulte de la transformation propre de la dérivée covariante.

Pour l'instant nous nous tenus à un formalisme abstrait, transposant ce que nous savions dans une nouvelle notation. Mais ce travail nous apporte deux choses. Le premier auquel nous avons déjà fait allusion, est la possibilité de décrire des champs de spineurs dans l'espace temps et d'en prendre la dérivée covariante. Nous ne poursuivrons pas cette piste. La seconde est un changement de point de vue sur les tenseurs permettant de les considérer comme des formes différentielles valorisées tensoriellement

Par exemple un objet comme X_m^a, que nous décrivons comme un tenseur mixte de type (1, 1) peut aussi être représenté par une "forme mono linéaire à valorisation tensorielle"(les arguments de la forme sont des tenseurs). Il a un indice grec et nous pouvons y voir une forme mono linéaire, mais il y a un vecteur qui correspond à chaque valeur de l'indice. De même un tenseur A_m_n^a_b, antisymétrique en m et , peut être interprété comme une forme bilinéaire valorisée par un tenseur(1, 1).

Alors , un tenseur avec quelques indices grecs antisymétriques et quelques index latins peut être interprété comme une forme différentielle , prenant ses valeurs dans la partie tensorielle D'habitude les formes différentielles sont valorisées par des scalaires L'intérêt de ce point de vue est manifeste quand nous considérons les dérivées extérieures. Si nous considérons X_m^a comme une forme mono linéaire valorisée par des vecteurs, nous sommes tentés d'en prendre la dérivée extérieure:

<TBODY>

(3.135) </TBODY>

Il est facile de vérifier que cet objet se transforme comme une forme bilinéaire ( c.a.d selon la loi de transformation des tenseurs (0, 2) par GCT's ( Transformation générale de coordonnées), mais pas comme un vecteur par LLT's (les transformations de Lorentz dépendent de la position, ce qui introduit un terme inhomogène dans la loi de transformation). Mais on peut y remédier en utilisant judicieusement une connexion de spin qui joue le rôle de forme mono linéaire. ( pas une forme mono linéaire dont les arguments sont des tenseurs du fait de la non tensorialité de la loi de transformation (3.134).) Alors l'objet :

<TBODY>

(3.136) </TBODY>

Comme vous pouvez le vérifier se transforme comme un tenseur.

Une application immédiate de ce formalisme est l'expression de la torsion et de la courbure, les deux tenseurs qui caractérisent une connexion. La torsion, avec ses deux indices antisymétriques peut être interprétée comme une forme bilinéaire T_m_n^a. dont les arguments sont des vecteurs. La courbure, antisymétrique dans ses deux derniers indices peut être interprétée comme une forme bilinéaire R^a_b_m_n. valorisée par des tenseurs(1, 1).

Equations de structure de Maurer-Cartan.

Usant de notre droit de supprimer des index, sur des formes différentielles, nous pouvons écrire les relations définissant ces tenseurs par :

<TBODY>

(3.137) </TBODY>

<TBODY>

(3.138) </TBODY>

Elles sont appelées les équations de structure de Maurer-Cartan. Elles sont équivalentes aux définitions habituelles, faisons ensemble l'exercice de le montrer pour la torsion, vous pourrez compléter de votre côté pour la courbure. Nous avons

<TBODY>

(3.139) </TBODY>

Ce qui est juste la définition que nous avons donné. Ici nous avons utilisé (3.131), l' expression pour les G^l_m_n en termes de tétrades et de connexion de spin. Nous pouvons aussi exprimer que ces tenseurs satisfont aux identités :

<TBODY>

(3.140) </TBODY>

<TBODY>

(3.141) </TBODY>

La première est la généralisation de R^r_[_s_m_n_] = 0, tandis que la seconde est l'identité de Bianchi Ñ_[_l_½R^r_s|_m_n_] = 0. (Quelquefois, les deux équations sont appelées l'identité de Bianchi .)

Dérivée extérieure covariante

La forme de ces expressions nous pousse irrésistiblement à la tentation de définir une "dérivée extérieure covariante", qui agit sur une forme linéaire à valorisation tensorielle en prenant la dérivée extérieure classique et qui ajoute les termes appropriés de connexion de spin, pour chaque index latin. Bien que nous ne le ferons pas ici, céder à cette tentation serait fondé, et en fait le membre de droite de (3.137) et les membres de gauche de (3.140) et (3.141) peuvent être interprétées justement comme des dérivées extérieures covariantes. Mais soyons prudents, comme (3.138) ne le peut pas, vous ne pouvez pas prendre une quelconque dérivée covariante d'une connexion de spin, car ce n'est pas tenseur..

Puisque nos équations sont vraies pour des connexions générales, regardons ce que nous obtenons pour une connexion de Christoffel. La contrainte d'absence de torsion se traduit par l'annulation de (3.137), Ceci ne conduit pas immédiatement à une conclusion simple sur les coefficients de la connexion de spin. La compatibilité métrique s'exprime par la nullité de la dérivée covariante de la métrique :g = 0. Nous voyons à quoi cela conduit quand nous exprimons la métrique dans la base orthonormée, où ses composantes sont simplement h_ab:

<TBODY>
		(3.142) </TBODY>

Poser ceci égal à zéro implique :

<TBODY>

(3.143) </TBODY>

Alors, la compatibilité métrique implique l'antisymétrie de la connexion de spin dans ses indices latins ( rappelons qu'une telle condition n'a un sens que si les deux index sont soit hauts soit bas ensembles). Ces deux conditions ensemble nous permettent d'exprimer la connexion de spin en termes de tétrades. Il y a une formule explicite pour cela, mais en pratique, le plus simple c'est de résoudre la condition de torsion nulle.

<TBODY>

(3.144) </TBODY>

Et en utilisant l'antisymétrie de la connexion de spin, de trouver les composantes individuelles.

Comparaison des connexions et de la courbure en géométrie de Riemann avec celle des théories de jauge en physique des particules.

Nous avons maintenant le formalisme nous permettant de comparer les connexions et la courbure en géométrie de Riemann avec celle des théories de jauge en physique des particules. C'est une digression, compréhensible par tous, mais non essentielle dans le cours de RG.

Dans ce cas, les champs qui nous intéressent sont décrits dans des espaces vectoriels définis en chaque point de l'espace temps. D'une part, en géométrie de Riemann, les espaces vectoriels incluent les espaces tangents, cotangents et des espaces tensoriels d'ordre supérieur construits à partir d'eux. D'autre part, dans les théories de jauge nous nous intéressons aux espaces vectoriels "internes". La différence est que les espaces tangents et ses associés sont intimement associés à la Variété et sont naturellement définis quand la Variété l'est, alors que les espaces internes peuvent être de n'importe quelle dimension et sont ajoutés indépendamment de la Variété.

Faisceau de fibres

En jargon mathématique, l'union de la Variété de base et d'espaces vectoriels internes (définis en chaque point) s'appelle un faisceau de fibres, et chaque copie d'un espace vectoriel est appelé la fibre (en accord avec notre définition du faisceau tangent). A côté de la Variété de base, ( pour nous l'espace temps) et les fibres, l'élément important dans la définition d'un faisceau de fibres est la "structure de groupe", un groupe de Lie qui s'applique sur les fibres pour décrire comment elles sont assemblées et réunifiées sur leurs recouvrements. Sans rentrer dans les détails, le groupe de structure pour le faisceau tangent dans un espace temps à quatre dimensions, est GL (4,), le groupe de matrices 4 × 4 inversibles, et si nous avons une métrique Lorentzienne il peut se réduire au groupe de Lorentz SO(3, 1). Considérons un espace vectoriel tridimensionnel et combinons les fibres avec les rotations classiques, la structure de groupe de ce nouveau faisceau est alors SO(3). Un champ supporté par ce faisceau peut être noté F^A (x^m), où A vaut de un à trois, c'est un vecteur tridimensionnel (interne et non référencé à l'espace temps) en chaque point de la Variété. Nous pouvons choisir librement la base dans les fibres, ce qui signifie que les grandeurs physiques doivent être conservées sous des transformations locales SO(3) comme décrit ci dessous :

<TBODY>

(3.145) </TBODY>

Où O^A'_A(x^m) est une matrice de SO(3) qui dépend de l'espace temps.

Transformations de jauge, théories de jauge.

De telles transformations sont appelées transformations de jauge, et les théories invariantes par elles sont appelées " théories de jauge."

Il n'est pas difficile, pour la plus grande partie, d'arranger les choses pour que les grandeurs physiques soient conservées par des transformations de jauge. La seule difficulté concerne la dérivée partielle ¶_mF^A. Car, comme la matrice O^A'_A(x^m) dépend de l'espace temps, elle va introduire un terme indésirable lors de dérivation partielle. Nous savons comment y remédier, introduire une connexion pour corriger le terme indésiré résultant de la loi de transformation.

Nous définirons donc la connexion sur un faisceau de fibres comme un objet A_m^A_B, à deux index de groupe et un index pour l'espace temps. Elle se transforme comme une forme monolinéaire par une transformation générale de coordonnées, alors que par une transformation de jauge elle se transforme comme

<TBODY>

(3.146) </TBODY>

(Attention, nos conventions sont drastiquement différentes de celles utilisées en physique des particules, et cela pose problème d'interprétation)

Dérivée covariante de jauge

Avec cette loi de transformation, la "dérivée covariante de jauge "

<TBODY>

(3.147) </TBODY>

Transforme "tensoriellement" par des transformations de jauge, ce que vous êtes invités à vérifier. ( En électromagnétisme, la connexion est simplement le potentiel vecteur conventionnel, aucun index n'est nécessaire car le groupe de structure est U(1) ).

Il apparaît clairement que la notion de connexion dans faisceau de fibres interne est très étroitement reliée à la connexion du faisceau tangent, particulièrement dans la description du référentiel orthonormé que nous avons discuté. La loi de transformation (3.146), par exemple est exactement la même que la loi de transformation (3.134) pour la connexion de spin. Nous pouvons aussi définir une courbure ou un tenseur "intensité de champ" qui est une forme bilinéaire,

<TBODY>

(3.148) </TBODY>

En correspondance exacte avec (3.138). Nous pouvons transporter parallèlement les objets le long de chemins, et il existe un équivalent au propagateur parallèle, la trace de la matrice obtenue par le transport parallèle d'un vecteur le long d'une boucle est appelée une " boucle de Wilson".

Nous pourrions poursuivre notre examen des relations entre les faisceaux tangents et les faisceaux de vecteurs internes, mais le temps nous est compté et nous avons d'autres chats à fouetter.

Des différences subsistent

A contrario, pour finir, insistons sur la différence fondamentale entre les deux constructions. La différence réside dans le fait que le faisceau tangent est intimement lié à la Variété qui le supporte, alors que les autres faisceaux de fibres sont "rajoutés" sans aucun rapport.

Cela a un sens de dire qu'un vecteur de l'espace tangent au point p "pointe le long d'un chemin" passant par p, cela n'en n'a pas pour un faisceau interne de vecteurs. Il n'existe pas d'équivalent à une base de coordonnées pour un espace interne, les dérivées partielles le long des courbes n'existent pas pour des vecteurs internes. Il s'ensuit que les tétrades qui relient les bases orthonormées aux bases de coordonnées, également n'ont pas leur place dans ce monde interne. Le tenseur de torsion, en particulier, n'est défini que pour une connexion dans le faisceau tangent et n'a aucun sens pour une connexion d'une théorie de jauge, étant la représentation d'une dérivée extérieure covariante d'une tétrade, objet qui n'existe pas dans un faisceau interne.

Ceci nous aura permis quand même d'apprécier les relations entre les différents usages de la notion de connexion, sans pour autant se laisser égarer.