Une Introduction, pas trop débile, à la Relativité Générale

1- Introduction

2- Relativité Restreinte

3- Tenseurs

4- Courbure

5- Relativité générale

6- Solution de Schwarzschild et trous noirs

7- Cosmologie

Sean M. Carroll

Enrico Fermi Institute and department of Physics

University of Chicago, Chicago, IL, 60637

Carroll@theory.uchicago.edu

2001

( Traduction Jacques Fric Juin 2002)

1-Introduction

La Relativité générale (RG) est la plus belle théorie jamais inventée. Cependant, elle a la réputation (justifiée) d'être extrêmement difficile à comprendre, principalement pour deux raisons: Il y a des tenseurs partout et l'espace temps de référence est courbe. Ces deux points obligent les utilisateurs de la RELATIVITÉ GÉNÉRALE à utiliser un langage particulier qui nuit à sa compréhension par les non initiés. Pourtant il est possible (et c'est ce que ce document vous propose de faire) de saisir les concepts de base de la théorie, même si vous n'êtes pas Einstein (et qui l'est ?).

La Relativité générale peut se résumer à deux propositions:

a- L'espace temps est une Variété courbe pseudo Riemannienne munie d'une métrique de signature ( - + + + ). (A noter que sur ce point on trouve aussi la convention équivalente inverse (+ - - -), mais on préfère de plus en plus la première qui n'a qu'un seul signe -).

b- La relation entre la matière (énergie) et la courbure de l'espace temps est décrite par l'équation (d'Einstein):

R_mn - 1/2 . R.g_mn = 8p G.T_mn (1)

Naturellement ces deux propositions sont totalement incompréhensibles à celui qui ne maîtrise pas le jargon. C'est par là que nous allons commencer.

Vous remarquerez, que cette introduction très pragmatique, a l'ambition de vous donner les bases du langage de la RELATIVITÉ GÉNÉRALE, pour vous faire comprendre au moins de quoi on parle, ( il faut commencer par là) et de vous présenter quelques points saillants de la théorie dans l'espoir de piquer votre curiosité afin de vous encourager à une lecture plus approfondie. Il ne se substitue en aucun cas à cette étude plus approfondie nécessaire si vous voulez comprendre les fondements de la théorie, ce qui, il faut le reconnaître représente un travail très conséquent et un bon niveau mathématique. Certains aspects de la Relativité Générale dans ce document sont introduits "ex abrupto" ou de façon intuitive, vous en trouverez en général la démonstration rigoureuse dans le cours détaillé du même auteur " Lectures notes on general relativity"

Une remarque: Les physiciens adorent poser les constantes égales à l'unité. Nous ne poserons pas la constante de Newton G =1, mais nous le ferons pour c ( c=1 implique que si l'unité de temps est la seconde, l'unité de longueur est la distance parcourue par la lumière en une seconde) Si c'est utile nous la réintroduirons facilement en cohérence avec l'équation aux dimensions: exemple si on a E = m, bien entendu c'est E = mc²) .

Comme ouvrages de référence sur la GR nous recommandons " A first course in general relativity " par Bernard Schutz, de niveau très accessible et pour ceux qui ont une formation scientifique supérieure "General Relativity " par Wald, "Gravitation and Cosmology" par Weinberg, "Gravitation" par Misner, Thorne et Wheeler et "Introducing Einstein's Relativity" par D'Inverno.

Bien sûr le mieux est de se connecter au site <http://pancake.uchicago.edu/~carroll/notes>, où vous trouverez les nouvelles fraîches sur le sujet, cette introduction ayant pour but de vous vous permettre d'en tirer profit.

2- Relativité Restreinte

La Relativité Restreinte ( RR) s'appuie sur la constance de la vitesse de la lumière dans les référentiels inertiels. Ceci aboutit à une conception où l'espace et le temps sont liés pour former l'espace temps, le facteur de conversion entre les unités de temps et d'espace est c, (c=1 rappelez vous). Les coordonnées d'espace temps peuvent être choisies comme suit :

x⁰ = ct = t

x¹ = x

x² = y

x³ = z (2)

Ce sont des Coordonnées cartésiennes. Juste une remarque de notation, les index hauts ne sont pas des exposants, ce ne sont que des indices. Ils vont de 0 à 3, l'ensemble des quatre coordonnées est dénoté x^µ.

Quelques conventions: les indices grecs représentent les coordonnées d'espace temps, occasionnellement nous utiliserons des indices latins qui ne représentent que les composantes spatiales: i =1,2,3.

La scène sur laquelle la RELATIVITÉ RESTREINTE se joue est une Variété particulière à quatre dimensions appelée l'espace temps de Minkowski ( quelquefois Espace de Minkowski). Les x^µ sont les coordonnées dans cette Variété. Les éléments de cet espace temps sont les évènements, un événement est spécifié par ses coordonnées d'espace et de temps. Les vecteurs dans l'espace temps sont attachés à un événement (pas de vecteurs libres qu'on pourrait déplacer ad libidum). Comme l'espace temps a quatre dimensions, ils sont souvent appelés quadri vecteurs et notés V^µ ou plus simplement V.

Nous avons aussi une métrique dans l'espace de Minkowski, h_mn. La métrique nous donne un moyen de définir la norme d'un vecteur, ou le produit scalaire de deux vecteurs. Ecrite sous forme matricielle la métrique de Minkowski est

ê -1 0 0 0 ê

ê 0 1 0 0 ê

h_mn = ê 0 0 1 0 ê (3)

ê 0 0 0 1 ê

Alors le produit scalaire de deux vecteurs est défini par

A.B = h_mnA^mBⁿ = - A⁰B⁰ + A¹B¹ +A²B² + A³B³ (4)

(Nous utilisons toujours la convention de sommation dans laquelle les indices hauts et bas identiques sont sommées sur toutes les valeurs possibles).

Ce produit scalaire permet de définir la distance infinitésimale ( au carré) entre deux points, appelée intervalle d'espace temps:

ds² = h_mn dx^mdxⁿ (5)

= - dt² + dx² + dy² + dz² (6)

En fait une équation de la forme (6) est souvent appelée la métrique. La Métrique contient toute l'information sur la géométrie de la Variété. La métrique de Minkowski est, bien sûr, juste la généralisation à l'espace temps du produit scalaire ordinaire sur un espace Euclidien plat (où on a pris l'habitude d'oublier le terme correspondant au tenseur métrique Euclidien du fait qu'il est unitaire et que nous pouvons représenter par le symbole de Kronecker d_ij.). Nous disons que la métrique de Minkowski a une signature ( - + + + ), quelquefois appelée "Lorentzienne " par opposition à la signature de la métrique Euclidienne qui ne comporte que des signes +. (Rappel: on trouve aussi la convention inverse + - - - ).

Notons que pour une particule de coordonnées spatiales xⁱ fixes, l'intervalle écoulé quand le temps passe est négatif, ds² = - dt² <0. Ceci nous conduit à définir le temps propre t via

dt² = - ds² (7)

Le temps propre écoulé sur d'une trajectoire de l'espace temps est le temps effectivement mesuré par l'observateur qui suit cette trajectoire. D'autres observateurs mesureront des temps différents.

Un peu de vocabulaire : Un vecteur V^µ de norme négative, V.V < 0 est dit de type temps, si la norme est nulle de type nul (ou encore lumière) et s'il est positif de type espace. De ce fait les trajectoires de ds² négatif (pas le temps propre) sont dites de type temps etc.. Ces concepts nous amènent naturellement au concept de diagramme d'espace temps, que vous connaissez sans doute. L'ensemble des trajectoires nulles issues et aboutissant à un événement constituent le cône de lumière, ce qui est explicité sur la figure qui suit.

Fig 1: Le cône de lumière représenté sur un diagramme d'espace temps. Les points dont l'intervalle d'espace temps est de type temps par rapport à l'origine sont à l'intérieur du cône, ceux de type nul sur la surface et ceux de type espace à l'extérieur.

Un chemin dans l'espace est spécifié par les quatre coordonnées d'espace temps fonction d'un paramètre, x^µ (l ). Un chemin est caractérisé de type temps, nul ou espace selon que son vecteur tangent dx^µ /dl est de type temps, nul ou espace. Pour les chemins de type temps, le paramètre le plus approprié est le temps propre, que nous pouvons calculer le long d'un chemin de type temps arbitraire via

t = ò (- ds²)^1/2 = ò [- h_mn (dx^m/dl)( dxⁿ/dl) ] ^1/2 .dl (8)

Le vecteur U^µ = dx^µ /dt est appelé le vecteur quadri-vitesse et est automatiquement normalisé

h_mn U^mUⁿ = -1 (9)

comme il est facile de la vérifier.

Un autre vecteur associé important est le vecteur quadri impulsion, défini par

p^µ = m.U ^µ (10)

où m est la masse de la particule. Cette masse est une quantité constante indépendante du référentiel, que l'on peut interpréter comme la masse au repos. L'énergie d'une particule est alors simplement p⁰, la composante de type temps du vecteur quadri impulsion. Dans le référentiel repos nous avons p⁰ = m , comme nous avons posé c = 1 , nous retrouvons la fameuse équation E = mc². Dans un référentiel en mouvement nous pouvons trouver les composantes de p^µ. en effectuant une transformation de Lorentz, pour une particule animée d'une tri vitesse v = dx/dt le long de l'axe des x nous avons

p^µ = ( gm,vgm, 0,0) (11)

où g = (1-v²)^-1/2 (rappel c =1) . Pour v petit , ceci donne p⁰= m + (1/2)mv², que nous interprétons comme l'énergie au repos plus l'énergie cinétique) et p¹= mv ( que nous interprétons comme l'Impulsion Newtonienne).

3- Tenseurs

La transition d'un espace plat à un espace courbe signifie qu'il ne sera éventuellement plus possible d'utiliser les coordonnées Cartésiennes. En fait un système de coordonnées passablement plus compliqué va se révéler nécessaire. Pour notre propre intérêt , nous voulons de plus que nos équations restent invariantes par tout changement de ces coordonnées (covariance générale). Si une équation est valable dans un système de coordonnées elle doit donc l'être dans tous. Il apparaît que beaucoup de paramètres que nous allons manipuler en RELATIVITÉ GÉNÉRALE vont être représentés par des tenseurs. On peut se représenter les tenseurs comme des vecteurs qu'on peut munir d'un plus grand nombre d'indices, dont la propriété caractéristique est de se transformer par changement de coordonnées x^µ ® x^µ' suivant la règle suivante, appelée loi de transformation des tenseurs: [ donnée sur un exemple de tenseur de rang 3, deux fois covariant (indices bas) et une fois contravariant (indice haut), les indices primés correspondant aux composantes dans le nouveau système de coordonnées x^µ'] ,

S^m'_n'r' = (¶x^m'/¶x^m)(¶xⁿ/¶x^n')(¶x^r/¶x^r') S^m_nr (12)

Remarquons que les indices non primés dans le membre de droite sont des indices opératoires, qui sont sommés sur toutes leurs valeurs possibles et ainsi disparaissent ne laissant que les indices primés du membre de gauche. La forme (12) est assez facile à mémoriser, si on pense à la "conservation des indices": Les indices hauts et bas libres ( non opératoires, donc primés dans notre exemple) doivent être les mêmes des deux côtés de l'équation. Cette règle est valable pour n'importe quelle équation tensorielle , pas seulement pour la loi de transformation ( règle syntaxique). Rappelez vous qu'un indice haut ne peut être sommé qu'avec un indice bas de même nom opératoire ( et vice versa). Comme il n'y a aucun système de coordonnée préférentiel en RELATIVITÉ GÉNÉRALE, cela nous incite à établir nos équations sous forme tensorielle, car si une équation entre tenseurs est valable dans un système de coordonnées , elle le sera dans tous.

Les tenseurs ne sont pas aussi compliqués que ce qu'on pense généralement. Ce ne sont que des objets géométriques qui sont la généralisation du concept de vecteur bien connu. Remarquons que les scalaires sont des tenseurs de rang 0 ( pas d'indices), les vecteurs sont des tenseurs avec un indice haut (contravariant) un tenseur avec deux indices en particulier un haut et un bas peut être représenté par une matrice, bien sûr les tenseurs peuvent comporter autant d'indices que l'on veut.

Cependant, il y a tout un vocabulaire que vous devez acquérir. Si un tenseur a n indices hauts et m indices bas, on l'appelle un tenseur de type ou de rang (n,m). Les indices hauts sont appelés indices contravariants (Formellement, un indice contravariant se réfère à un espace vectoriel, dans lequel sont définies les composantes "ordinaires" d'un vecteur "ordinaire", comme ceux que vous connaissez bien, à trois dimensions par exemple, dans une base quelconque), et les indices bas sont appelés covariants (relatifs à l'espace vectoriel dual des formes linéaires appliquées sur l'espace vectoriel associé à un vecteur ordinaire correspondant). Cela est un peu formel, mais pas très compliqué. D'ordinaire on se réfère à cela en parlant simplement d'indices hauts et d'indices bas, ce qui compte tenu des règles syntaxiques de manipulation des indices est plus pratique.

Des tenseurs de type ( n,m) peuvent être contractés pour former un tenseur de type ( n-1, m-1) en sommant un de ses indices haut sur un de ses indices bas.

S^m = T ^ml_l (13)

La contraction d'un tenseur à deux indices est souvent appelée la trace (qui est un scalaire, ce qui se justifie si on y pense un peu).

Si un tenseur est invariant par permutation d'indices

S .._{lµ …} = S .. _{µl …} (14)

Alors il est dit symétrique vis à vis de ces deux indices, si sa valeur change de signe

S .._{lµ …} = - S .. _{µl …} (15)

Alors il est dit antisymétrique. Un tenseur peut posséder ces propriétés sur un nombre quelconque de ses indices.

Il est possible de symétriser (antisymétriser) un tenseur quelconque, en effectuant les combinaisons linéaires appropriées. Cette procédure de symétrisation, antisymétrisation est notée en encadrant les indices concernés entre parenthèses ou entre crochets.

T _{(µ1µ2..µn)} = (1/n!)(T _µ1µ2..µn + somme sur les permutations des indices µ₁..µ_n )

T _{[µ1µ2..µn]} = (1/n!)(T _µ1µ2..µn + somme alternée sur les permutations des indices µ₁..µ_n) (16)

Par somme alternée, nous entendons que les permutations qui sont le résultat d'un nombre impair de permutations sont affectées du signe moins alors :

T _{[µnr] s} = 1/6 ( T _{µnr s} - T _{µrn s} + T _{rµn s} - T _{nµr s} + T _{nrµ s} -T _{rnµ s}) (17)

Le tenseur le plus important en RELATIVITÉ GÉNÉRALE est le tenseur métrique g_µn, une généralisation ( à des coordonnées et une géométrie arbitraires ) de la métrique de Minkowski h_µn. Bien que h_µn soit juste un cas particulier de g_µn, nous le notons par un symbole différent pour souligner l'importance du passage d'un espace plat à un espace courbe. Le tenseur g_µn est un tenseur symétrique à deux indices. Un point important est qu'il est toujours possible de trouver un système de coordonnées tel qu'en un point spécifié p, les composantes de la métrique sont celles de la métrique de Minkowski (3) et que les dérivées premières de cette métrique s'annulent. Autrement dit, la métrique paraît plate précisément en ce point. Par contre, en général on ne peut pas annuler les dérivées secondes de g_µn, en raison précisément de la courbure locale de l'espace temps.

Même si l'espace temps est plat , la métrique peut avoir des dérivées qui ne s'annulent pas si le système de coordonnées n'est pas Cartésien. Par exemple en coordonnées sphériques ( espace) nous avons

t = t

x = r sinq cos j

y = r sinq sin j

z = r cosq (18)

Ce qui conduit directement à

ds² = - dt² + dr² +r² dq² + r² sin²q dj (19)

soit

ï-1 0 0 0 ï

ï 0 1 0 0 ï

g_µn = ï 0 0 r² 0 ï (20)

ï 0 0 0 r²sin²q ï

Remarquons qu' il est souvent plus simple de trouver les nouvelles composantes du tenseur en insérant nos transformations de coordonnées directement dans l'expression différentielle du ds² ( par exemple, dz = cosq.dr - r. sinq.dq ), plutôt que d'utiliser la loi de transformation des tenseurs (12).

Comme dans l'espace de Minkowski, nous utilisons la métrique pour calculer le produit scalaire.

A.B =g_mn A^m Bⁿ (21)

Ceci suggère, en tant que notation abrégée, le concept d'abaissement des indices.

A partir de n'importe quel vecteur, nous pouvons construire un tenseur (0,1) défini par la contraction par la métrique.

A_n =g_mn .A^m (22)

Ainsi le produit scalaire devient g_mn A^m Bⁿ = A_n Bⁿ . Nous pouvons aussi définir la métrique inverse g^mn comme la matrice inverse du tenseur métrique.

g^mn .g_nr = d_r^m (23)

avec d_r^m symbole de Kronecker ( espace temps). Vous pouvez vous convaincre que cette expression correspond vraiment à une multiplication de matrice ( En fait les composantes correspondantes à celles du tenseur métrique, du tenseur métrique inverse sont les cofacteurs divisés par le déterminant, du déterminant associé au tenseur métrique)

Donc nous avons aussi la possibilité d'élever des indices.

A^m = g^mn .A_n (24)

Remarquons qu'élever un indice sur la métrique produit le symbole de Kronecker , en conséquence :

g^mn . g_mn = d_µ^m = 4 (25)

En dépit de l'ubiquité des tenseurs il est quelquefois utile de considérer des objets non tensoriels.

Un exemple important est le déterminant du tenseur métrique

g = det (g_mn ) (26)

Un calcul direct montre que sous une transformation de coordonnées x^µ ®x^µ', le déterminant ne se transforme pas selon la loi de transformation des tenseurs ( sous laquelle il devrait être invariant s'il était un tenseur, car ce serait un tenseur [0,0] sans indices, donc un scalaire) , mais à la place:

g = [det (¶x^m' /¶x^m)]^-2. g (27)

Le facteur det (¶x^m' /¶x^m) est appelé le Jacobien de la transformation. Les objets qui se transforment selon cette loi (impliquant des puissances du Jacobien) sont appelés des densités de tenseurs.

Le déterminant g est quelquefois appelé " densité de scalaire". Un autre exemple de densité est l'élément de volume d⁴x = dx⁰dx¹dx²dx³

d⁴x = det (¶x^m' /¶x^m) d⁴x (28)

Nous pouvons donc définir un élément de volume invariant en multipliant d⁴x par la racine carrée de (- g) , ainsi le facteur Jacobien disparaît :

(-g )^1/2 d⁴x = (-g )^1/2 d⁴x (29)

En coordonnées cartésiennes par exemple, nous avons (-g )^1/2 d⁴x = dtdxdydz, tandis qu'en coordonnées polaires ceci devient r²sinq.dt.dr.dq.dj. Alors les intégrales de fonctions sur l'espace temps sont de la forme ò f(x^m)(-g )^1/2 d⁴x. ("Fonction" signifie ici évidemment la même chose que "scalaire"). Un autre objet qui n'est malheureusement pas un tenseur est la dérivée partielle ¶/¶ x^m (¶_µ en abrégé). Appliquée à un scalaire, la dérivée partielle produit un tenseur du meilleur crû, en effet en utilisant la règle de chaînage habituelle nous avons:

¶_µ f ®¶_µ' f = (¶ x^m /¶ x^m' ) ¶_µf (30)

En accord avec la loi de transformation des tenseur. Mais sur un Vecteur V^m, étant donné que V^m' = (¶ x^{m '} /¶ x^m )V^m , nous avons

¶_mVⁿ ® ¶ _m'V^n' = [(¶ x^m /¶ x^m' ). ¶_µ ][(¶ x^n' /¶ xⁿ). Vⁿ]

= (¶ x^m /¶ x^m' ) (¶ x^{n '} /¶ xⁿ )¶_mVⁿ + (¶ x^m /¶ x^m' ) (¶² x^{n '} /¶ x^m .¶ xⁿ) V^m (31)

Le premier terme nous plait bien, mais le second gâche tout. Nous allons donc définir une dérivée covariante d'un tenseur qui est égale à la dérivée partielle corrigée par un terme linéaire appliqué au tenseur original.

(32)

Ici le symbole Gⁿ_ml représente un ensemble de nombres appelés coefficients de connexion, munis d'une loi de transformation appropriée choisie pour annuler le terme non tensoriel dans (31). Donc nous devons avoir

(33)

Alors nous sommes certain que Ñ_m V^µ se transforme comme un tenseur. Le même genre d'artifice marche pour définir une dérivée covariante pour les tenseurs munis d'indices bas, nous introduisons simplement un signe moins et changeons l'indice opératoire de sommation.

(34)

S'il y a de multiples indices, pour chaque indice haut nous introduisons un terme avec un + G et pour chaque indice bas un terme avec un -G .

(35)

C'est l'expression générale de la dérivée covariante.

Que se cache t'il derrière sont ces mystérieux coefficients de connexion ? Par chance nous pouvons en donner une expression en fonction uniquement de la métrique et de ses dérivées.

(36)

Nous vous laissons le soin de vérifier que le terme de droite a bien la loi de transformation désirée. Vous pourrez également vérifier que les coefficients de connexion sont symétriques dans leurs indices bas G^s_mn = G^s_nm . Ces coefficients peuvent être non nuls même dans un espace plat, en cas de coordonnées non cartésiennes. Il existe d'autres types de coefficients de connexion, que nous n'utiliserons pas ici. Ces coefficients particuliers que nous avons choisis sont appelés Symboles de Christoffel, et ce sont ceux qu'on utilise en RELATIVITÉ GÉNÉRALE. De la valeur de ces coefficients il s'ensuit que la dérivée covariante de la métrique et de son inverse sont identiquement nuls, cette propriété est appelée la compatibilité métrique.

Ñ_sg_mn = 0 , Ñ_sg^mn = 0 (37)

Ainsi, pour une métrique donnée g_mn, nous calculons les coefficients de connexion permettant de réaliser des dérivées covariantes. Beaucoup d'équations familières de la physique dans un espace plat continuent à être valables en remplaçant les dérivées partielles par les dérivées covariantes correspondantes.

Ainsi en RELATIVITÉ RESTREINTE, les champs de vecteurs Magnétiques et Electriques B et E peuvent être rassemblés au sein d'un même tenseur antisymétrique de rang deux. F_mn:

( 38)

et la densité de charge électrique r et le vecteur courant J peuvent être rassemblés dans un quadri vecteur J^m

J^m = (r, J) ( 39)

Dans cette notation les équations de Maxwell

(40)

se réduisent à deux relations.

( 41)

Ces équations sont valides dans l'espace de Minkowski, mais leur généralisation à un espace courbe est immédiate, on remplace ¶_m ®Ñ_m

( 42)

Ce sont ces équations (42) qui régissent l'électromagnétisme en Relativité Générale.

4- Courbure

Nous avons évoqué le concept de courbure de l'espace temps sans en donner une définition précise. Pour comprendre, il faut d'abord introduire la notion de Variété. Fondamentalement, une Variété est un espace éventuellement courbe, dans lequel une région suffisamment petite (infinitésimale en réalité) ressemble à un espace plat. La terre par exemple nous paraît plate parce que nous n'en voyons qu'une toute petite partie ( alors que globalement elle est ronde).

Une caractéristique essentielle d'une Variété est qu'elle a le même nombre de dimensions partout. Si on colle l'extrémité d'une corde à un plan, l'ensemble n'est pas une Variété car il est partiellement à deux dimensions et partiellement à une.

Les exemples les plus connus de Variété sont l'espace plat à n dimensions Rⁿ ("R" pour nombre réel) et l'Hyper Sphère Sⁿ de dimension n. Ainsi R¹ est une ligne réelle, R² est le plan, etc.., alors que S¹ est le cercle , S² la sphère ( sa surface) etc..

Nous utiliserons en général, les coordonnées "sphériques" ( r, q , f ), sur S² ( qui est la surface de la sphère). Dans ces conditions, avec r =1, la métrique sur S² est

ds² = dq² + sin²df² (43)

Le fait que les Variétés peuvent présenter une courbure rend la vie moins monotone, comme vous vous en doutez. Mais la plupart des problèmes rencontrés dans les espaces courbes, sont aussi présents dans les espaces plats si on utilise des coordonnées non Cartésiennes. Le problème avec les espaces courbes, c'est qu'on ne peut jamais utiliser de coordonnées Cartésiennes, car elles ne peuvent décrire que des espaces plats. Alors les outils et méthodes à développer pour des systèmes de coordonnées non Cartésiennes vont être essentiels, en fait nous avons déjà pratiquement fait ce travail.

Il n'est pas surprenant, que l'information sur la courbure d'une Variété soit contenu dans la métrique, la question est : Comment l'extraire. On peut l'obtenir à partir de G^s_mn , par exemple, car sa valeur est nulle ou non nulle selon le système de coordonnées (comme nous l'avons vu en espace plat). Pour des raisons que nous ne développerons pas ici, l'information sur la courbure est intégralement contenue dans un tenseur de rang quatre, appelé tenseur de Riemann de Courbure.

Cet objet extrêmement important ( développé par Riemann vers 1860, bien avant la Relativité) est donné en termes de symbole de Christoffel par la formule.

( 44)

Le signe global est conventionnel, dans d'autres documents vous pouvez trouver la signe contraire.

Remarquons que le tenseur de Riemann est construit à partir d'éléments non tensoriels (dérivées partielles et symboles de Christoffel mais dont la combinaison produit un tenseur comme vous pouvez le vérifier avec la loi de transformation).

Une propriété importante de ce tenseur est qu'il s'annule (toutes ses composantes sont nulles) si et seulement si l'espace est plat.

Opérationnellement, "plat" signifie qu'il existe un système de coordonnées global dans lequel les composantes de la métrique sont constantes partout.

Le Tenseur de Riemann peut être contracté, il produit le tenseur de Ricci puis le scalaire de Ricci qui sont très utiles en RELATIVITÉ GÉNÉRALE. Le tenseur de Ricci est donné par

(45)

Bien qu'il semble qu'on puisse faire d'autres contractions indépendantes, du fait des symétries du tenseur de Riemann ( discuté ci après), c'est la seule contraction indépendante.

La trace du tenseur de Ricci produit le scalaire de Ricci:

(46)

qui est un autre élément très utile en RELATIVITÉ GÉNÉRALE.

Bien que le tenseur de Riemann ait quatre indices, et donc 256 composantes, compte tenu de ses nombreuses (anti)symétries, seulement 20 d'entre elles sont indépendantes. Ci dessous quelques unes des propriétés du tenseur de Riemann exprimées sur sa version totalement covariante ( tous les indices bas).

(47)

Ceci implique que le tenseur de Ricci est symétrique.

(48)

En plus de ces identités algébriques, le tenseur de Riemann obéit à une identité différentielle.

(49)

Celle ci est quelquefois appelée l'identité de Bianchi. Si nous définissons un nouveau tenseur, le tenseur d'Einstein par

(50)

Alors l'identité de Bianchi implique que la divergence de ce tenseur est identiquement nulle.

(51)

Ceci est quelquefois appelé l'identité de Bianchi contractée.

Il y a deux choses à connaître impérativement au sujet de la courbure: Le tenseur de Riemann et les géodésiques. Vous connaissez le tenseur de Riemann, passons aux géodésiques.

De façon informelle , une géodésique est "le plus court chemin entre deux points". Plus formellement, une géodésique est une courbe qui extrémiste la fonction de longueur ò ds. Supposons un chemin paramétré par l, c.a.d x^m(l). La distance infinitésimale le long de la courbe est donnée par

ds=ôg_mn (dx^m/dl)( dxⁿ/dl) ô ^1/2 .dl (52)

La longueur totale de la courbe est

L = ò ds ( 53)

Pour trouver la géodésique dans une géométrie donnée nous avons donc à faire un calcul variationnel sur (53) compte tenu de (52) pour ds et rechercher l'extremum de L. Par chance de grands esprits sont passés par là et ont déjà fait le calcul. La réponse est que x^m(l) est une géodésique si elle satisfait à la fameuse équation géodésique.

(54)

( Insistons sur le fait que l'équation géodésique s'établit uniquement à partir de considérations géométrique sur les Variétés, sans aucune référence à la RELATIVITÉ GÉNÉRALE)

En fait cela n'est vrai que si l est un paramètre affine , c'est à dire relié au temps propre par la relation

l = at + b ( 55)

En pratique , c'est le temps propre qui est le plus souvent utilisé comme paramètre affine (pour les géodésiques de type temps en tout cas). Dans ce cas , le vecteur tangent est la quadri vitesse U^m = dx^m / dt , et l'équation géodésique peut être écrite

d U^m /d t + G^m_rs U^rU^s = 0 (56)

La raison physique pour laquelle les géodésiques sont si importantes est qu'en RELATIVITÉ GÉNÉRALE, les corps d'épreuve se déplacent sur des géodésiques. Si ces corps sont sans masse, ces géodésiques sont de type lumière ( ds² =0) , et s'ils sont massifs les géodésiques sont de type temps (ds²<0). Remarquons que le formalisme qui nous a conduit à dire "extremum" pour une géodésique plutôt que "minimum" trouve sa justification dans le fait que, pour des particules massives sur la géodésique, le temps propre est maximum ( ce qui explique le paradoxe des jumeaux, celui qui reste à la maison sur une géodésique subit un temps propre maximum, donc est plus vieux, que celui qui a voyagé et qui n'est donc pas resté sur cette géodésique, lorsqu'ils se retrouvent).

Et maintenant, le quart d'heure philosophique. Avant la RELATIVITÉ GÉNÉRALE, la physique Newtonienne disait " les particules non soumises à des forces suivent une ligne droite", la gravitation étant l'une de ces forces parmi d'autres. Maintenant en RELATIVITÉ GÉNÉRALE la gravitation est représentée par une courbure de l'espace temps, pas par une force. Du point de vue de la RELATIVITÉ GÉNÉRALE, les particules se meuvent sur des géodésiques si elles ne sont pas soumises à des forces, forces dont la gravitation est exclue. Si nous considérons , le mouvement de particules soumises à d'autres forces que gravitationnelles ( électromagnétiques par exemple) , elles ne se déplaceront pas sur des géodésiques, nous pouvons toujours utiliser (54) pour décrire leur mouvement, mais nous devons ajouter un terme représentant la force en question dans le membre de droite. Dans ce sens l'équation géodésique est quelque chose comme l'expression dans un espace courbe de

F = mg = 0

5- Relativité Générale.

Le passage des mathématiques à la physique implique l'introduction d'équations dynamiques pour décrire les relations entre la matière et l'énergie et la courbure de l'espace. En RELATIVITÉ GÉNÉRALE, "l'équation du mouvement" pour la métrique est la fameuse équation d'Einstein

(57)

Remarquons que le membre de gauche correspond à l'expression du tenseur d'Einstein G_mn donnée par (50). G est la constante de Newton ( pas la trace G_mn ). T_mn est un tenseur symétrique de rang 2, appelé le tenseur Energie Impulsion. Il contient tout ce que nous devons connaître sur l'énergie et l'impulsion des champs de matière, qui agissent comme source de gravitation. Donc le membre de gauche de l'équation mesure la courbure de l'espace , et le membre de droite l'énergie et l'impulsion qu'il contient. Simplement génial!

Les composantes T_mn du tenseur énergie impulsion représentent le flux de la m^ième composante de l'impulsion dans la n^ième direction. Enoncé ainsi c'est quasi incompréhensible et peu utile, concrètement, considérons une forme de matière qu'on affectionne particulièrement en RELATIVITÉ GÉNÉRALE à savoir un fluide parfait, défini comme un fluide isotrope dans son référentiel repos. Ceci signifie qu'il n'a ni viscosité ni perte calorique, il est alors entièrement défini par sa densité d'énergie r et sa pression p dans son référentiel repos ( isotrope , identique à lui même dans toutes les directions). Si U^µ désigne la quadri vitesse d'un élément du fluide , le tenseur énergie impulsion prend alors la forme.

(58)

Si nous élevons un indice et tenons compte de la normalisation des vitesses g^mnU_mU_n= -1, nous obtenons une version plus explicite

( 59)

Si T_mn contient tout ce que nous devons connaître de l'énergie et de l'impulsion, il doit satisfaire aux lois associées de conservation. En fait cela s'énonce en termes mathématiques par la nullité de la divergence covariante.

Ñ^m T_mn= 0 (60)

Rappelons nous que l'identité de Bianchi (51) garantit que la divergence du tenseur d'Einstein est identiquement nulle. Donc l'équation d'Einstein garantit la conservation d'énergie impulsion. Bien sûr , c'est une relation locale. Si nous intégrons ( par exemple) la densité d'énergie rsur une hyper surface de type espace, la quantité correspondante n'est pas constante dans le temps. Il n'y a pas en RELATIVITÉ GÉNÉRALE la notion de conservation globale de l'énergie. La relation (60) exprime la conservation locale, et la présence de la dérivée covariante autorise le transfert d'énergie entre la matière et les champs gravitationnels.

L'apparente opacité de l'équation d'Einstein, ne doit pas nous masquer le fait qu'elle est une extension naturelle de la gravitation Newtonienne. Pour s'en convaincre considérons l'équation de Poisson relative au potentiel Newtonien f

Ѳf = 4pG (61)

où r est la densité de matière. Dans le membre de droite nous avons un opérateur différentiel du deuxième ordre appliqué sur le potentiel de gravitation f. Ceci est proportionnel à la densité de matière. Comme la RELATIVITÉ GÉNÉRALE est une théorie complètement relativiste, la densité de matière doit être remplacée par son équivalent invariant par transformation, le tenseur énergie impulsion T_mn . Pour être similaire à (61), ceci doit être proportionnel à un tenseur de rang 2 agissant comme un opérateur différentiel du second ordre sur le champ gravitationnel décrit par la courbure de l'espace en RELATIVITÉ GÉNÉRALE qui dépend uniquement de la métrique. De la définition de G_mn en termes de g_mn , c'est exactement ce que le tenseur d'Einstein fait. En fait G_mn est le seul tenseur de rang deux, construit sur des dérivées premières et secondes de la métrique dont la divergence covariante est nulle.

L'équation de la RELATIVITÉ GÉNÉRALE a bien la même forme que celle de Newton. De plus , l'équation de la RELATIVITÉ GÉNÉRALE doit "converger" vers celle de Newton dans les conditions de la "limite Newtonienne" suivantes: Vitesse des particules faible par rapport à "c", champ gravitationnel faible ( ce qui permet de le considérer comme une perturbation de l'espace plat) , et champ statique. Considérons une métrique qui est presque celle de Minkowski, la différence étant qu'on a rajouté une sorte particulière de (petite) perturbation:

ds² = -(1+2f) dt² + (1-2f) dx² (62)

Où f est une fonction des coordonnées spatiales xⁱ . Si nous substituons ceci dans l'équation géodésique et que nous le résolvons pour la vitesse classique ( tri vitesse) utilisant le fait que comme les particules se meuvent lentement, c'est une bonne approximation, nous obtenons

d²x/dt² = -Ñf (63)

où Ñ représente ici l'opérateur de divergence spatiale classique ( pas la dérivée covariante). Ceci n'est autre que l'équation d'une particule se déplaçant dans un champ gravitationnel Newtonien de potentiel f. Si par ailleurs nous calculons la composante 00 du membre de gauche de l'équation d'Einstein:

R₀₀ -1/2 Rg₀₀ = 2Ѳf (64)

La composante 00 du membre de droite de l'équation est simplement ( au premier ordre des petites valeurs de f et r)

8pGT₀₀ = 8pGr (65)

Donc l'équation d'Einstein appliqué à la métrique (62) produit

Ѳf = 4pGr (66)

Ce qui est précisément l'équation de Poisson (61). Donc dans cette limite la RELATIVITÉ GÉNÉRALE converge avec la gravitation Newtonienne.

Bien que l'équation complète non linéaire d'Einstein (57) paraisse simple, dès qu'on cherche à l'appliquer, on se rend compte qu'il n'en n'est rien. Si on se souvient de la définition du tenseur de Riemann en termes de symboles de Christoffel, et de leur définition en termes de Métrique, on réalise la complexité de cette équation. Elle est également hautement non linéaire et de ce fait difficile à résoudre. Si nous prenons la trace de (57) , nous obtenons

- R = 8pGT (67)

Insérant ceci dans (57) nous donne une autre forme de l'équation d'Einstein

(68)

Cette forme est très utile si nous considérons le cas où nous sommes dans le vide, pas d'énergie impulsion. Dans ce cas T_mn = 0 et (68) devient l'équation d'Einstein dans le vide:

R_mn = 0 (69)

Ceci est déjà plus simple à résoudre que l'équation complète.

Un dernier mot sur l'équation d'Einstein : Elle peut être dérivée d'un Lagrangien très simple, L= (-g) ^{1/2 .} R , avec g déterminant de la métrique et R scalaire de Ricci ( plus un terme approprié pour les champs de matière). En d'autres termes , l'action en RELATIVITÉ GÉNÉRALE est simplement

S = ò d⁴x (-g) ^{1/2 .} R ( 70)

L'équation d'Einstein correspond à l'extremum de cette action ( d'Hilbert) par rapport aux variations de la métrique g_mn. Enoncé ainsi, c'est beaucoup plus élégant .

6- La solution de Schwarzschild et les trous noirs

Pour résoudre l'équation d'Einstein, nous somme amenés en général à faire des hypothèses simplificatrices. Par exemple dans beaucoup de situations physiques, nous avons une symétrie sphérique. Si nous voulons résoudre l'équation pour une métrique g_mn, cette symétrie nous simplifie la tâche, car indépendamment de la RELATIVITÉ GÉNÉRALE un calcul formel nous montre que la métrique générique associée ( en coordonnées sphériques) est de la forme

ds² = - A ( r,t) dt² + B (r,t) dr² + r² (dq² + sin²q df² ) (71)

où A et B sont des fonctions positives de (r,t), et vous reconnaîtrez la métrique sur une sphère décrite en (43).

Si nous insérons cette métrique dans l'équation d'Einstein, nous allons obtenir une solution pour une distribution de matière sphérique. Pour être encore plus restrictif, considérons l'équation dans le vide (69). Alors il y a une solution unique :

(72)

avec

C'est la célèbre métrique de Schwarzschild, solution de l'équation d'Einstein. Le paramètre m, est la masse conventionnelle Newtonienne contenue à l'intérieur de la sphère de rayon r considéré. Un fait remarquable est que la métrique de Schwarzschild est l'unique solution à l'équation d'Einstein, dans le vide pour une distribution de matière à symétrie sphérique. Ce fait , conséquence du théorème de Birkhoff, signifie que même si la matière oscille largement, le champ gravitationnel à l'extérieur n'est pas perturbé, aussi longtemps que la symétrie sphérique est conservée.

Un point de philosophie : Les composantes de la métrique "explosent" pour r = 0 et r = 2Gm. En principe, tout point en lequel les composantes de la métrique sont infinis ou présentent une pathologie marginale est appelé un point singulier et présente une singularité. Ceci se divise en deux catégories, les singularités de coordonnées et les singularités "vraies". Une singularité de coordonnées signifie qu'on a choisi un système de coordonnées inapproprié, et peut s'éliminer par un changement de coordonnées. Une singularité vraie est une pathologie véritable de la géométrie de la Variété en ce point qui conduit à exclure le point de la Variété.

Dans la géométrie de Schwarzschild, le point r = 0 est une vraie singularité où la métrique n'est pas définie. Par contre le point r = 2Gm est simplement une singularité de coordonnées. Nous pouvons le montrer en effectuant une transformation qui conduit aux coordonnées de Kruskal définies par:

(73)

Dans ces coordonnées, la métrique (72) prend la forme

(74)

avec

Où r est une fonction implicite de u et v défini par

( 75)

En examinant (74), on voit que la singularité à r = 2Gm est éliminée. Le fait que nous puissions trouver des coordonnées où la singularité est éliminée montre qu'il s'agissait d'une simple singularité de coordonnées. La chose intéressante avec la métrique de Schwarzschild est qu'elle décrit aussi bien des objets très familiers comme le système solaire que des objets plus exotiques comme les trous noirs. Pour s'en rendre compte regardons comment les particules se déplacent dans la géométrie de Schwarzschild. On s'aperçoit qu'on peut traiter le problème d'une particule se déplaçant dans le plan q = p/2 comme un problème unidimensionnel relatif à la coordonnée r = r (t). Autrement dit, la distance d'une particule au point r = 0 est solution de l'équation

( 76 )

C'est tout simplement l'équation du mouvement d'une particule de masse unitaire et d'énergie E dans un potentiel unidimensionnel V ( r ). Ce potentiel pour la géométrie de Schwarzschild est donné par

( 77 )

Ici, L représente le moment angulaire par unité de masse de la particule et e est une constante égale à zéro pour les particules sans masse et + 1 pour les particules massives. Remarquons que le temps propre t est nul pour les particules sans masse , et que nous utilisons un autre paramètre l dans (76), mais l'équation reste la même. Donc pour trouver les orbites des particules en métrique de Schwarzschild, nous devons résoudre l'équation du mouvement d'une particule dans un potentiel central donné par (77). Notons que le premier terme est constant, que le second est identique à celui de la gravitation Newtonienne , que le troisième est la contribution du moment d'inertie de la particule, qui existe aussi en théorie Newtonienne. Seul le dernier terme de (77) est propre à la RELATIVITÉ GÉNÉRALE.

Ce terme supplémentaire a deux conséquences importantes. D'abord il agit comme une petite perturbation sur une orbite, ce qui conduit à la précession de l'orbite de Mercure par exemple, ensuite pour r très petit le potentiel gravitationnel en RELATIVITÉ GÉNÉRALE tend vers - ¥, ce qui signifie que si une particule s'approche trop près de r = 0, elle va être piégée et ne pourra jamais s'échapper.

Ceci est vrai dans le contexte de particules de test non soumises à d'autres forces, et ceci va également tenir pour des particules capables d'accélérer ( voir ci après). Rassurons nous, car avec une étoile comme le Soleil, dont la métrique de Schwarzschild ne décrit la situation qu'à l'extérieur, elles percuteront la surface du Soleil ( est ce plus enviable ?), avant d'approcher de la zone étrange où toute fuite est impossible. Pourtant il y a des situations où cela peut arriver.

Les trous noirs.

Un trou noir est un corps dont toute la masse s'est effondrée en deçà du point de non retour. Ce point de non retour situé à sur une surface à r = 2 Gm, est appelé l'horizon des évènements que l'on peut se représenter comme la "surface" du trou noir. Bien qu'il soit impossible de rentrer plus en détail, dans les propriétés intéressantes de l'horizon des trous noirs, les concepts de base ne sont pas difficiles à comprendre.

Du point de vue d'un observateur extérieur, une horloge tombant dans un trou noir, apparaît battre de plus en plus lentement à mesure qu'elle s'approche de l'horizon des évènements.

En fait un observateur extérieur ne verra jamais une particule de test traverser la surface à r = 2 Gm, il verra la particule s'en rapprocher indéfiniment mais de plus en plus lentement.

A contrario, il en serait autrement si vous étiez l'observateur de test tombant dans le trou noir, le temps vous apparaîtrait toujours se dérouler au même rythme, du fait que vous et votre Bracelet Montre sont dans le même référentiel inertiel, vous ne sentiriez jamais le temps se "ralentir".

Donc, atteindre l'horizon des événement ne réclamera pas un temps infini, bien au contraire, vous traversez l'horizon à toute allure. L'horizon franchi, vous vous trouvez projeté inéluctablement et très rapidement au point r = 0. L'horizon passé, il n'y a pas d'échappatoire, le temps coule dans la direction des "r" décroissants.

On peut voir cela sur la métrique ( 72) en notant que r devient une coordonnée de type temps pour r < 2 Gm. Le pire est que si vous essayez de contrarier ce mouvement en allumant des rétrofusées par exemple, cela ne fera que raccourcir l'échéance fatale du fait que la géodésique ( mouvement de chute libre) maximise le temps propre comme nous l'avons vu précédemment. En fait en raison des forces de marée colossales vous êtes déchiquetés très rapidement ( sauf pour des trous noirs très super massifs où l'effet de marée est moins prononcé). Le triste sort d'un astronaute au cœur d'un trou noir est décrit en détail dans Misner, Thorne et Wheeler p 860-862.

Le diagramme d'espace temps d'un trou noir en coordonnées de Kruskal (74) est montré sur la figure 2.

Ce qui est représenté correspond à une coupe de l'espace temps entier, correspondant aux coordonnées angulaires q = p/2 et f = 0. Il y a deux régions asymptotiques, une à u ® + ¥ et l'autre à u ® - ¥ , dans ces deux régions la métrique paraît approximativement plate. L'horizon des évènements est la "surface " r = 2 Gm, soit u = ± v. Dans ce diagramme tous les cônes de lumière sont à ± 45 °. A l'intérieur de l'horizon des évènements où r < 2 Gm, toutes les trajectoires de type temps conduisent à la singularité à r = 0. Insistons sur le fait que ce diagramme représente l'extension mathématique maximum de la solution de Schwarzschild, une solution complète de l'équation d'Einstein dans le vide , mais que cela ne correspond pas forcement à des solutions physiques réalistes. Pourtant pendant que nous y sommes évoquons un autre aspect encore plus étrange associé aux trous noirs: les trous de ver

Figure 2 : Le diagramme de Kruskal : la solution de Schwarzschild en coordonnées de Kruskal (74), où tous les cônes de lumière sont à ± 45°. La surface r = 2Gm est l'horizon des évènements, à l'intérieur de l'horizon des évènements , tous les chemins de type temps rencontrent la singularité à r = 0. Les parties droites et gauches du diagramme représentent deux régions de l'espace temps asymptotiquement plates distinctes. Chaque point du diagramme représente une sphère ( de rayon r)

Trous de ver

Le diagramme de Kruskal définit donc quatre régions décrites sur la figure 3, ci dessous.

Figure 3

La région I est notre espace, la région II est l'intérieur de la surface de l'horizon du trou noir que nous pouvons atteindre en un temps fini, donc qui fait partie de la Variété décrivant notre espace temps ( à l'exclusion de la singularité). Les parties III et IV "symétriques" sont plus inattendues. La région III correspond à une région où tout objet qui y est placé est "expulsé" vers la région IV, autre univers semblable au notre mais miroir où de la matière surgit ex nihilo au lieu d'y être absorbée ( trous blancs). Il ne semble pas qu'on puisse atteindre la région IV depuis la région I, pourtant..

On va voir qu'elle est connectée à la région I par un trou de ver, un goulot d'étranglement spatio-temporel reliant deux régions distinctes. Examinons le diagramme de Kruskal en le découpant en surfaces de type espace à v constant ( Figure 4)

Figure 4

Dessinons chaque tranche en restaurant une des coordonnées angulaires pour clarifier ( fig 5) (chaque cercle horizontal correspond alors à une sphère).

Le diagramme ci dessous est spatio-temporel.

u

Figure 5

Donc la géométrie de Schwarzschild décrit vraiment deux régions asymptotiquement plates qui mènent l'une vers l'autre, se connectent via un trou de ver pendant très un court instant puis se déconnectent. Mais les trous de vers se ferment trop rapidement pour qu'un observateur puisse passer d'une région à l'autre. Si on considère la vitesse liée à la coordonnée v = cte, on voit qu'elle est toujours supérieure à "c" pour passer : Un cas limite concerne les photons en orbite sur l'horizon qui peuvent passer par effet tunnel quantique ).

Cette histoire de deux espaces temps miroirs, séparés communiquant pendant un court instant puis se refermant parait assez invraisemblable. Il n'est pas sûr que cela se passe vraiment ainsi dans le monde physique car la métrique de Schwarzschild ne modélise pas avec précision l'univers entier. N'oublions pas qu'elle n'est valide que dans le vide, à l'extérieur des étoiles par exemple. Si cette étoile a un rayon supérieur à 2GM, nous n'aurons pas à nous soucier d'horizons.

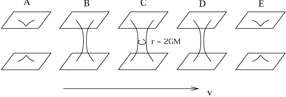
De plus, dans un trou noir formé par effondrement d'une étoile massive, les équations du vide sont plus restrictives et il n'y aura pas deux régions asymptotiquement plates, mais une seule, celle où l'étoile était située ( fig 6). En cela, des trajectoires de type temps ne pourront pas s'étendre dans les deux régions, et nous ne saurons pas dire si l'autre région existe vraiment.

Figure 6

Dans l'effondrement d'une étoile en trou noir, toute l'information relative à l'objet en cours d'effondrement est perdue, sa constitution, sa forme etc. Les seules informations conservées par le trou noir sont sa masse, son moment d'inertie et sa charge électrique. Ce fait, qu'on appelle le théorème "les trous noirs n'ont pas de poils" implique que la métrique du trou noir ne peur être fonction que de ces trois grandeurs seulement. Comme les trous noirs réels sont probablement électriquement neutres, nous ne présenterons pas les trous noirs chargés (la métrique de Reissner - Nordstrom).

Les trous noirs en rotation par contre présentent un intérêt considérable en astrophysique, ils sont décrits par la métrique de Kerr.

( 78)

( 79)

où a est le moment cinétique par unité de masse. Ces trous noirs sont plus complexes et ont sur le plan mathématique des propriétés encore plus étranges que les trous noirs de Schwarzschild ( cf cours détaillé).

Pour finir, parmi les nombreuses propriétés remarquables, signalons la conjecture de censure cosmique. Remarquez comment la singularité à r = 0 est cachée, dans la mesure où vous ne pouvez pas y accéder sans franchir l'horizon. Il est conjecturé que ceci est toujours vrai , dans toute solution de l'équation d'Einstein. Pourtant , des calculs numériques semblent mettre en cause cette conjecture, dans certains cas particuliers tout au moins.

7- Cosmologie

La méthode qui a conduit à la solution de Schwarzschild ( utilisation des symétries) peut être reconduite avec le même succès en Cosmologie sur l'hypothèse que l'Univers est homogène et isotrope dans ses trois dimensions d'espace ( pas en ce qui concerne le temps, puisqu'on constate qu'il est dynamique, définissant un passé et un futur différents). Cette propriété implique l'existence d'un référentiel repos pour l'Univers , qui définit une coordonnée de temps universelle et particularise des hyper surfaces tri dimensionnelles perpendiculaires à cette coordonnée. Dans l'Univers réel, ce référentiel repos est celui dans lequel les Galaxies sont statistiquement au repos et où le RFC est isotrope. L'Homogénéité signifie que la courbure de l'espace temps est la même en tout point à un temps t donné. L'Isotropie est un concept plus délicat, mais signifie que l'Univers est le même dans toutes les directions. Par exemple la surface d'un cylindre est homogène ( tous les points sont identiques) mais pas isotrope ( la direction parallèle à l'axe est privilégiée). Un cône est isotrope autour de son sommet mais pas homogène.

Ces hypothèses réduisent le choix de la métrique à trois formes, regroupées dans la métrique de Robertson Walker ( RW).

(80)

où k est une constante qui peut valoir -1 , 0 , ou +1. La fonction a(t) est appelée le facteur d'échelle, et nous indique la taille relative des hyper surfaces spatiales.

Les coordonnées ci dessus, sont appelées coordonnées Comobiles, car un point au repos par rapport au référentiel préférentiel de l'Univers a ses coordonnées r, q, f constantes. Le cas k = - 1 , conduit à une métrique correspondant à ce qui est appelé un Univers ouvert , dont les hypersurfaces typiques sont des hyperboloïdes à 3 dimensions ( Hyper selle de cheval, pour des hyper chevaux sans doute), le cas k = 0 correspond à un Univers plat dont les hypersurfaces de référence vont être des espaces Euclidiens 3D, le cas k = + 1, va correspondre à un Univers fermé, dont les hypersurfaces sont typiquement des hyper sphères 3D.

Remarquons que le terme " ouvert", "fermé" et "plat" ne s'applique qu'à la géométrie spatiale des hypersurfaces 3D, pas au destin temporel de l'Univers, à savoir s'il s' étendra indéfiniment ou se re-contractera après avoir atteint un maximum. Par ailleurs nous n'avons considéré que les topologies triviales simplement connexes.

Le volume d'un Univers fermé est fini, alors que les Univers plats ou ouverts ont des volumes infinis ( s'ils sont simplement connexes, autrement ils peuvent avoir des volumes finis par exemple un hyper tore ).

On peut écrire (80) dans d'autres systèmes de coordonnées en particulier si on pose :

r = (siny, y, sinhy) pour k = ( +1, 0, - 1) respectivement on obtient

ï[ dy² + sin²y ( dq² + sin²q.df²)] pour k = +1

ds² = - dt² + a²(t)ï[ dy² + y² ( dq² + sin²q.df²) ] pour k = 0

ï[dy² + sinh²y ( dq² + sin²q.df²)] pour k = -1 (81)

De plus le cas k = 0 peut être écrit en coordonnées quasi Cartésiennes

ds² = - dt² + a²(t) ( dx² + dy² + dz² ) soit

ds² = - a²(h) ( -dh² + dx² + dy² + dz² ) (82)

Dans la dernière expression, h est appelé le temps conforme et est défini par

h= ò dt/a(t) (83)

Les coordonnées (h,x,y,z) sont souvent appelées les "coordonnées conformes".

Comme la métrique RW est la seule métrique possible homogène, ce que nous avons à faire est de résoudre l'équation d'Einstein sur cette métrique, ce qui nous donnera a(t).

Si nous utilisons l'équation dans le vide nous ne trouvons que l'espace de Minkowski comme solution. Nous avons donc besoin d'introduire de l'énergie et de l'impulsion pour trouver quelque chose d'intéressant. Pour simplifier, nous allons assimiler le contenu de l'Univers à un fluide parfait de densité d'énergie r et de pression p. Dans ce cas l'équation d'Einstein produit deux équations différentielles pour a (t) ( en effet les 3 équations d'espace se ramènent à une seule du fait des symétries ), appelées équations de Friedmann.

(84)

Comme les équations de Friedmann déterminent l'évolution de la métrique de Robertson Walker, on parle souvent de Cosmologie FRW et même FLRW quand on inclut Lemaître.

L'expansion de l'Univers se mesure avec le paramètre de Hubble :

(85)

et la variation de ce paramètre dans le temps est caractérisée par le paramètre de décélération :

q = a".a/a'² = - ( 1 + H'/H²) (86)

Les équations de Friedmann peuvent être résolues si on choisit une équation d'état (entre r et p.), mais les solutions peuvent être complexes. La solution pour k = 0 est simple. Si l'équation d'état est p = 0, l'Univers est dominé par la matière et

a(t) µ t ^2/3 (87)

Dans un Univers dominé par la matière, la densité d'énergie décroît quand le volume s'accroît, donc

r _mat µ a ^-3 (88)

si p = r/3 , l'Univers est dominé par le rayonnement et

a (t) µ t ^1/2 (89)

Dans un Univers dominé par le rayonnement , le nombre de photons décroît quand le volume s'accroît, et l'énergie de chaque photon est décalée vers le rouge proportionnellement à a(t), donc

r _ray µ a ^-4 (90)

Si p = - r, alors l'Univers est dominé par le vide et

a(t) µ e ^Ht (91)

Un Univers dominé par le vide est aussi appelé, Univers de de Sitter. Dans un tel Univers, la densité d'énergie est constante, ainsi que le paramètre de Hubble, et ils sont liés par:

H (8pGr_vide/3)^1/2 = Constante (92)

Remarquons que quand a® 0, c'est r _ray qui croît le plus vite, donc , si nous retournons dans le passé nous devrions trouver une période dominée par le rayonnement . Par contre r_vide reste constant lorsque l'Univers s'étend, donc s'il n'est pas nul, et que l'Univers dure suffisamment longtemps, nous atteindrons éventuellement une phase dominée par le vide. Etant donné que nous constatons que l'Univers s'étend, nous pouvons nous demander s'il en sera ainsi pour toujours, ou si nous allons atteindre une limite au delà de laquelle une phase de contraction va commencer. Pour des sources d'énergie avec p et r ³ 0, ( incluant les Univers dominés par la matière et le rayonnement), les Univers fermés ( k = + 1 ) peuvent éventuellement se re contracter alors que les Univers ouverts s'étendent à jamais. Avec p et r < 0, les choses se compliquent, gardez juste en mémoire qu'il n'y a pas de correspondance fixe entre spatialement fermé/ouvert et temporellement fini/infini. Pour déterminer si l'Univers est ouvert ou fermé nous devons faire des observations. Dans un Univers plat, limite entre les deux cas, la densité est égale à la densité critique, et vaut

r _crit = 3 H²/8pG (93)

Notons que ceci évolue au cours du temps , actuellement elle est de 5 x 10^-30 grammes/cm³

Notre Univers sera ouvert si la densité est inférieure à cette valeur, fermé dans le cas contraire. Donc il est utile de définir le paramètre de densité

W = r/r _crit = 3 H²r/8pG = 1 + k/a'² (94)

Cette valeur change également au cours du temps sauf si elle est strictement égale à 1. Un Univers ouvert est caractérisé par W < 1, un Univers fermé par W > 1.

Nous avons déjà mentionné le décalage vers le rouge des photons dans un Univers en expansion. Un photon émis avec une longueur d'onde l₁ à un temps t₁, va être observé avec une longueur d'onde l₀ à un temps t₀ conformément à :

l₀/l₁ = a (t₀)/a(t₁)

(95)

Définissons le décalage vers le rouge z comme l'accroissement relatif en longueur d'onde.

z = l₀ - l₁ / l₁ = (l₀/l₁ ) - 1 = [a (t₀) /a(t₁) ] - 1 ( 96)

Gardez à l'esprit que ceci mesure seulement l'expansion nette de l'Univers entre le temps d'émission et le temps de réception, et n'a rien à voir avec un effet Doppler , qui résulterait d'une vitesse relative entre les deux, rappelez vous que le cadre de Relativité Générale est un Espace temps décrit par une Variété Riemannienne et que dans ce contexte, ces vitesses ne sont en général pas bien définies. (cf cours détaillé). Cependant il est habituel d'en parler comme si le décalage vers le rouge était dû à un effet Doppler résultant d'une vitesse relative entre la source et l'observateur, sur le plan strictement mathématique, ceci n'a aucun sens dans ce contexte, même si pour les faibles valeurs de z cela peut se ressembler. Alors la constante de Hubble décrit la relation entre la distance s ( mesurée sur une hyper surface de type espace) et le décalage vers le rouge entre une source et l'observateur

z = H (t₀).s (97)

Ceci est bien sûr la relation linéaire découverte par Hubble.