
Mise à jour le 24 Avril 2016
CONFÉRENCE DE Gilles COHEN-TANNOUDJI
du LARSIM (Laboratoire de Recherche sur les Sciences de la Matière)
«ÉMERGENCE DE LA MATIÈRE ET DE L'ÉNERGIE SOMBRES À PARTIR DU VIDE QUANTIQUE DU MODÈLE STANDARD DE LA PHYSIQUE DES PARTICULES.»
Organisée par la SAF
Dans ses locaux, 3 rue Beethoven, Paris XVI
Le Samedi 19 Mars 2016 à 15H00
à l'occasion de la réunion de la Commission de Cosmologie.
Photos : JPM pour l'ambiance. (Les photos avec plus de résolution peuvent m'être demandées directement)
Les photos des slides sont de la présentation de l'auteur. Voir les crédits des autres photos si nécessaire
(Le conférencier a eu la gentillesse de nous donner sa présentation complète (en pdf) elle est disponible sur le site de la commission et également disponible sur ma liaison ftp au téléchargement et s'appelle.
Saf-cosmo-GCT.pdf elle est dans le dossier COSMOLOGIE SAF de la saison 2015-2016).
Ceux qui n'ont pas les mots de passe doivent me contacter avant.
Pour info les actualités cosmo présentées ce jour là sont aussi disponibles sur le site de la commission.
BREF COMPTE RENDU

Une salle trop
pleine due à la qualité de notre orateur ! La commission travaille à
trouver une solution agréable pour tous.

Notre conférencier est bien connu de la SAF et du public
en général, il a fait toute sa carrière au CEA et aujourd'hui il est
professeur émérite au LARSIM au CEA-Saclay.
Il met à la disposition des internautes, son blog, un site extraordinaire qu’il fait vivre régulièrement :http://www.gicotan.fr/
Le titre de la conférence d’aujourd’hui est effectivement un peu complexe :
« Émergence de la matière et de l'énergie sombres à
partir du vide quantique du modèle standard de la physique des
particules »
Et je ne sens pas capable tout seul de faire un compte rendu complet.
Heureusement quelqu’un a entendu mon appel (voir plus bas)
Voici en introduction, le résumé que GCT nous propose :
Le nouveau modèle cosmologique standard,
"LambdaCDM" est marqué par la découverte de deux composantes (matière
et énergie sombres) représentant 95% du contenu total de l'univers, qui
ne trouvent pas d'explications dans le cadre du modèle standard de la
physique des particules.
Je montrerai que la cosmologie LCDM
peut être interprétée, du fait des deux phases d'inflation qu'elle
comporte (l'inflation primordiale et l'inflation tardive liée à la
constante cosmologique) comme une cosmologie
n'impliquant pas de coût énergétique, c'est-à-dire d'émergence à partir
d'un état d'énergie nulle, le "vide".
En théorie quantique des champs, au fondement du modèle standard de la physique des particules le "vide" est l'état
fondamental, à zéro particule, du système des champs quantiques en
interaction, un milieu complexe, siège de fluctuations quantiques, d'où
peuvent émerger aussi bien la partie visible de l'univers que ses
composantes sombres.
Tout part de l’équation d’Einstein :
 Cette équation lie la géométrie de l'espace-temps à la répartition de matière et d'énergie.
Cette équation lie la géométrie de l'espace-temps à la répartition de matière et d'énergie.
R est le tenseur de Ricci qui caractérise la courbure spatio-temporelle. T est le tenseur énergie-matière.
Ces équations sont valables dans tout l’Univers.
Les équations d’Einstein correspondent à l’espace-temps à 4 dimensions.
La matière dit à l’espace-temps comment il doit se courber, et l’espace-temps dit à la matière comment elle doit bouger.
Dans un premier temps, Einstein élimine la constante
lambda, puis en 1917 voulant obéir au principe de Mach, avec un Univers
fermé sans bord, il la réintroduit. Cela correspond à une gravité
négative.
C’est Alexandre Friedman, qui utilise les équations d’Einstein dans un contexte d’univers isotrope et homogène.
Ces équations, sont en fait connues sous le nom de FLRW (Friedman Lemaître Robertson Walker)
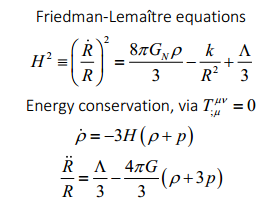
Ces équations relient le taux d’expansion de l’Univers
(la constante de Hubble H), la courbure k et le facteur d’échelle R à la
densité d’énergie r .
Lambda est le terme d’énergie noire, p la pression.
Le taux d’expansion : H = R’/R
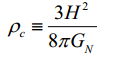
L’équation possédant un signe moins, il existe donc une densité critique.
De plus la conservation de l’énergie implique :
![]()
Avec
de g à dr : énergie totale, énergie baryonique (mat visible)
énergie de radiation (négligeable) énergie de matière noire et énergie
de l’énergie sombre.
Et là, je dis à l’aide !!!
 Et c’est notre ami, Jean Pierre TREUIL
qui a pris plus de notes que moi et qui a enregistré l’orateur et l’a
recontacté, qui nous donne un compte rendu extrêmement complet que je
reproduis ci-après ; un grand
merci à lui
Et c’est notre ami, Jean Pierre TREUIL
qui a pris plus de notes que moi et qui a enregistré l’orateur et l’a
recontacté, qui nous donne un compte rendu extrêmement complet que je
reproduis ci-après ; un grand
merci à lui
Il nous a semblé utile, pour mieux rendre compte de cet exposé, de rappeler
quelques notions ou modèles qui en forment partiellement l’arrière
plan, et sur lesquelles Gilles Cohen-Tannoudji est plusieurs fois
revenu. Il s’agit :
1. Du
principe de Mach
2. De la
constante cosmologique et de sa place dans les équations d’Einstein
3. Du modèle
d’Univers de de Sitter
4. De
l’histoire thermique de l’Univers
Du principe de Mach.
Partons
de la manière dont notre conférencier mentionne ce principe, lorsqu’il
explique l’introduction par Einstein, dans les équations de la
Relativité générale, de la constante cosmologique : savoir que “les
propriétés de l’espace-temps sont entièrement dues à la matière”.
Einstein imagine en effet une cosmologie avec, pour que le “Principe de
Mach” soit vérifié, un univers fermé (fini, sans bord). Mais alors les
équations d’Einstein
sans constante cosmologique conduisent inévitablement à une contraction
progressive de cet univers fini, à son effondrement, sous l’effet de la
gravitation. L’introduction de la constante cosmologique, avec une
valeur positive, est là pour compenser la gravitation et maintenir un
univers fermé statique.
Ainsi la volonté que son univers soit “machien” a conduit Einstein à réactiver cette constante cosmologique qu’il avait d’abord écarté.
Ce principe de Mach
pose le postulat suivant : un observateur, placé dans un espace par
ailleurs totalement vide de matière hormis quelques objets proches qui
lui sont liés, ne peut, par aucune expérience physique (mesures de
forces d’inertie s’appliquant à ces objets), décider s’il se meut dans
l’espace
autour de lui par un mouvement accéléré, notamment s’il est en rotation
autour de lui même. La constatation d’une telle accélération par la
mesure de forces d’inertie, ne se manifestera qu’avec l’existence de
matière “lointaine”, non liée à l’observateur, dont la distribution
fournit le référentiel implicite à partir duquel un second observateur
peut observer le mouvement du premier.
Le
principe de Mach renvoie à la question de savoir si un espace vide, sans
matière, peut avoir une quelconque réalité physique. On conçoit que
cette question puisse être au cœur de la réflexion de notre
conférencier.
De la constante cosmologique et de sa place dans les équations d’Einstein
Gilles
Cohen-Tannoudji n’explicite pas pourquoi Einstein, recherchant un
univers machien, est conduit à l’idée d’un univers fini.
En
dehors du fait que dans un tel univers, on n’a pas à se préoccuper des
conditions aux limites à l’infini, et à vrai dire, puisque cet univers
est fermé et donc sans bord, on n’a à se préoccuper d’aucunes conditions
aux limites. La nature fini de l’univers exige alors on l’a dit, une
force qui équilibre la gravitation, une “gravitation négative”, d’où on
l’a vu, l’introduction de la constante cosmologique dans les équations.
L’écriture
des équations (locales) d’Einstein place le plus souvent l’intervention
de la constante cosmologique dans la partie gauche des équations ;
ainsi pose t-on (avec c=1) :
![]()
Cela paraît logique : le facteur 𝚲
s’appliquant au tenseur métrique s’inscrit dans la partie gauche, la
part géométrique de l’équation. La partie droite capturant le contenu
“matériel “ de l’univers, le tenseur énergie
impulsion. Mais on peut aussi bien écrire :
![]()
Ce
faisant on place la constante cosmologique du coté droit, assimilant le
terme où elle intervient à une sorte de “contenu matériel”, différent de
la “matière ordinaire”. Bien sûr, l’équation n’a plus son bel
équilibre, puisque le tenseur métrique intervient à la fois comme
facteur de
𝚲 dans la partie droite et dans le calcul du tenseur d’Einstein dans la partie gauche.
Mais cette assimilation du champ métrique à un contenu matériel est ici encore à la racine des idées présentées.
Du modèle d’univers de de Sitter.
Un univers de de Sitter est
un univers dans lequel il n’y a aucun contenu matériel : le tenseur
énergie impulsion est uniformément nul. On peut aussi le définir comme
un univers dans lequel la constante universelle de gravitation est
nulle.
On
impose également qu’il soit homogène et isotrope ; il est donc une
solution particulière des équations FLRW (Friedmann, Lemaître,
Robertson, Walker), applications des équations d’Einstein aux cas
d’univers possédant ces qualités.
Dans un tel univers, la dynamique est entièrement contrôlée par la constante cosmologique, supposée positive.
L’accélération du facteur d’échelle (application au cas de la seconde équation de Friedmann) est
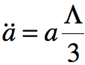
Le taux de croissance du facteur d’échelle, ou paramètre de Hubble H, est donné (application de la première équation de Friedmann) par :
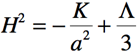
Ces équations simples montrent que la croissance du facteur d’échelle a(t) est “très vite” (=, dès que le temps cosmique t est suffisamment grand) exponentielle - le paramètre de Hubble gardant alors une valeur constante √(𝝠/3)
; et que le paramètre de courbure spatiale K n’a plus de réelle
influence : l’univers peut être vu comme spatialement plat avec K=0.
Les
univers de de Sitter fournissent les modèles d’expansion inflationnaire,
dont Gilles Cohen-Tannoudji nous parlera longuement.
Rayon de Hubble et facteur d’échelle.
Dans
son exposé, Gilles CohenTannoudji s’est beaucoup servit d’une
représentation de la dynamique de l’univers sous la forme d’un graphe 1/H versus a, reliant l’évolution dans le temps du rayon
de Hubble 1/H(t) et celle du facteur d’échelle a(t)
Le paramètre de Hubble H est par définition le taux d’expansion du facteur d’échelle, soit 1/a da/dt.
Le rapport 1/H a la dimension d’un temps, le temps de Hubble.
C’est l’intervalle de temps cosmique qui sépare l’instant t où
H et a sont mesurés du temps où le facteur d’échelle serait nul
(a=0), si la dérivée da/dt avait toujours été
la même qu’à cet instant t.
Autrement dit, si par exemple t
est l’instant actuel, c’est l’âge qu’aurait l’univers si la croissance
par unité de temps du facteur d’échelle était restée constante, avec sa
valeur d’aujourd’hui.
A ce temps de Hubble correspond naturellement une distance, celle parcouru par la lumière en ce même temps.
Cette distance est le rayon de Hubble, que l’on peut aussi écrire 1/H dans un système ou c=1.
Voyons donc comment se relient 1/H et a, en éliminant t dans les équations donnant leur évolution dans le temps.
Dans
les équations capturant la dynamique d’expansion de l’univers (équations
FLRW + équation de conservation de l’énergie), les seules grandeurs sur
le contenu matériel qui interviennent sont une densité r
et une pression p.
Cette densité est la somme d’une densité de matière “ordinaire” ou “baryonique” (non relativiste )
rb
protons, neutrons, électrons, d’une densité de matière noire rdm , et enfin d’une
densité de rayonnement, ou plus exactement de matière relativiste rr
photons, neutrinos… .
La présence de la constante cosmologique peut s’interpréter formellement comme l’intervention d’une quatrième densité constante rL
valant L/(8p
G N ), une densité d’énergie sombre . Si la courbure spatiale K est nulle (univers spatialement plat) ou encore si le carré du facteur d’échelle (soit a ²)
est suffisamment grand devant K, la première équation de Friedman se réécrit alors :
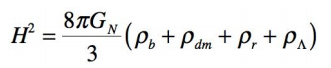
L’évolution
divergente des densités au cours du temps a pour origine l’impact de
l’expansion de l’univers combiné aux différences d’équations d’état de
forme p = w r
reliant les densités et les
pressions respectives de ces quatre fluides : matière baryonique et
matière noire, qui interviennent de façon identique, avec w b = 0, w dm = 0, c.a.d. matière sans pression ;matière relativiste,
avec w r = ⅓ ;
énergie sombre, avec w ᵶ =
1 .
Dans la dynamique du modèle cosmologique standard L
CDM, on distingue alors trois phases distinctes, selon la prépondérance
de chaque type de densité : une première phase où la dynamique est
dominée par le
rayonnement ;une seconde où elle est dominée par la matière (ordinaire
et noire) ;une dernière où cette dynamique est dominée par l’énergie
sombre.
Ainsi dans chaque phase l’équation de conservation s’écritelle, en éliminant la variable pression :
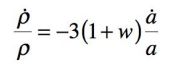
D’où l’on tire :
![]()
Dans la phase dominée par le rayonnement, la densité diminue comme (1/a)⁴ et dans celle dominée par la matière, comme (1/a)³.
Dans la phase dominée par l’énergie sombre, elle reste constante, égale comme il se doit à rL =
L/(8p G N ), et finit donc bien par l’emporter.
Dans la première équation de Friedman, ne conservons cas d’école que la densité dominante de la phase considérée.
Le report dans cette équation de la relation entre ᵰ et a conduit au lien entre le rayon de Hubble et le facteur d’échelle :
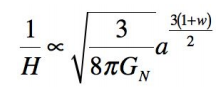
Ce que l’on peut écrire (Avec la convention habituelle où l’indice 0 affecté à une grandeur identifie la valeur actuelle de cette grandeur. Dans tout ce qui suit nous considérons par convention que ce temps actuel est inclus dans la phase où l’équation se trouve valide. Ce n’est
évidemment pas le cas dans la réalité
: nous ne sommes plus dans la phase dominée par le rayonnement !)
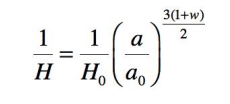
Ainsi, dans la phase dominée par le rayonnement, le rayon de Hubble augmentetil comme a^2, dans la phase dominée par la matière
comme a^(3/2). Il reste constant dans la phase dominée par l’énergie sombre.
Par
ailleurs on peut déduire mathématiquement de ces équations la variation
du facteur d’échelle (Résolution des équations différentielles dites de
Bernouilli, ici sous la forme simple da/dt = k a^(n+1).) en fonction du
temps :
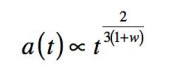
Ainsi, dans les phases où l’on peut négliger la constante cosmologique, et où les fluides respectent une équation d’état avec w >1 , le facteur d’échelle
a augmente avec le temps, il y a bien expansion, une expansion dont le taux diminue comme 1/t
Univers observable et horizons
A plusieurs reprises, Gilles CohenTannoudji a parlé de l’univers observable, et de l’horizon des évènements.
Ces
notions méritent qu’on y reviennent, toujours dans perspective d’une
bonne compréhension de son exposé, et dans l’esprit du schéma 1/H versus a sur lequel il s’est appuyé.
Une première acception d’univers observable.
Dans ce premier sens, l’univers
observable est, l’ensemble des évènements dont la lumière émise (où et
plus généralement tout signal relativiste) nous parvient maintenant,
à nous observateurs sur la Terre.
Dans le temps le temps de “regard en arrière” cet univers observable est limité par l’âge
J de l’univers ;l’expression de cette limite est :
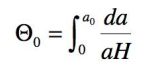
En appliquant l’expression de 1/H en fonction de a, donnée précédemment,
cette limite dans le temps se réécrit :
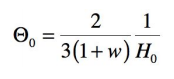
Parmi
les différentes notions de distance utilisables en cosmologie, retenons
ici, pour représenter le “rayon” de cet univers observable à l’instant
actuel, la distance radiale comobile entre l’objet
émetteur et l’observateur.
L’expression de cette distance est :
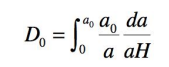
En reportant l’expression de 1/H, le rayon (évalué en distance comobile) de notre univers observable (ici et
maintenant) se réécrit :
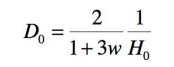
Pour faire un calcul plus exact il faudrait tenir compte des variations dans le temps et donc avec a du coefficient w
;la valeur de ce dernier est en effet ⅓ dans la phase dominée par le rayonnement et est nulle dans la phase dominée par la matière.
Et donc décomposer en deux sommes les intégrales précédentes, de a=0 à a = ar puis de ar
à a0.
La
notion d’univers observable se généralise à d’autres instants que
l’instant “actuel”. L’univers observable suit l’observateur dans le
parcours de sa ligne d’univers. Son rayon s’identifie au rayon d’un horizon appelé
l’horizon des particules.
Partons toujours de “nous même”, observateurs de l’univers, non plus nécessairement à l’instant actuel, le facteur d’échelle valant a 0, mais à un instant t
et un facteur d’échelle a quelconque.
L’horizon des particules sépare, dans l’espace
pris à cet instant t notons le avec la convention souvent utilisée
S t :
1. Les “particules” qui ont pu, dans le passé,
avoir été observées,
et donc nous “impacter” d’une certaine façon
2. Les “particules” qui ne pouvaient être observées, car
encore trop éloignées pour que leur lumière ait eu le temps de nous parvenir.
Ce
terme de particules mérite éclaircissement. L’horizon des particules ne
sépare pas en effet des évènements observables et des évènements non
observables se produisant dans l’espace St.
Il introduit une coupure entre
1) des points de l’espace St (Points supposés matérialisés par des “particules”) potentiellement siège, dans le passé, d’évènements qui ont ou
auraient pu être observés,
2) des points du même espace St où aucun évènement ayant eu lieu dans le passé n’auraient pu être observés.
Autrement dit, le contenu matériel de l’espace en deçà de l’horizon
possède un passé que nous avons pu connaître, dont nous avons pu garder une certaine trace.
La distance (comobile) à l’horizon des particules, le rayon D(a) de cet espace a étant
le facteur d’échelle à l’instant t considéré
s’exprime par une formule similaire à
la précédente, le principe du calcul étant le même :
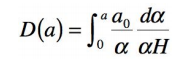
Où a est le facteur d’échelle
à un instant quelconque entre 0 et t .
En reportant dans cette expression la valeur de 1/H en fonction de a et de w , le calcul montre que cette intégrale
est convergente, et il vient :
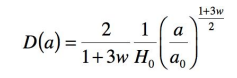
Ou encore, en exprimant le rayon de l’horizon en fonction du taux d’expansion H existant au même instant
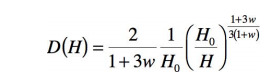
Lorsqu’on
évalue ce rayon d’horizon non plus en distance comobile, mais en
distance physique, donc en multipliant la distance comobile par le
facteur d’échelle, le calcul amène alors une formule très simple :
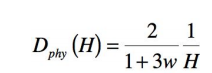
Au cours du temps, cette distance physique à l’horizon des particules augmente comme le rayon de Hubble.
Une seconde acception d’univers observable en fait une notion “intemporelle”.
Dans cette seconde acception, l’univers observable est la région de
l’espace temps constituée de l’ensemble des évènements qui peuvent être
observés (“un jour”) par un observateur éternel, autrement dit les évènements
dont cet observateur peut avoir connaissance.
Par construction, la taille de cet univers observable ne se modifie pas avec le temps propre de l’observateur éternel.
La frontière d’avec le reste de l’univers (à jamais nonobservable) s’identifie avec ce qui est appelé l’horizon
des évènements.
En se plaçant à un instant t du temps propre de l’observateur éternel, l’horizon des évènements sépare, dans
l’espace St
1. Les évènements se produisant dans cet espace
(donc à l’instant t ), qui pourront un jour être observés par l’observateur de référence.
2. Les évènements se produisant dans ce même espace (donc
toujours à l’instant t ), mais qui ne pourront jamais être observés par ce même observateur.
La distance à l’horizon, exprimé en fonction du facteur d’échelle a existant à l’instant t , est donnée par
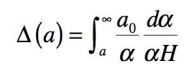
Le calcul tenant compte de l’expression de 1/ H pour les phases dominées par le rayonnement et la matière ( w>⅓
) montrent que cette intégrale n’est
pas convergente . Ainsi, dans le cas théorique d’un univers plat et
d’une constante cosmologique nulle, l’horizon des évènements n’existe
pas, son rayon étant infini. Pour le définir malgré tout, il faudrait le
tronquer supérieurement, en renonçant à tenir compte des évènements
dont l’observation n’aurait lieu que dans des périodes trop éloignées.
L’intégrale est par contre convergente en deçà de w = ⅓, et en particulier
pour un univers de de Sitter, dominée par la constante cosmologique. Dans ce cas, H étant
constant et pris égal à H0 , le calcul amène
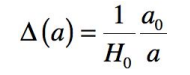
Le rayon comobile des évènements diminue au cours du temps comme
1/a , donc très rapidement, avec une décroissance exponentielle en e^(H0 t). Le champ comobile des évènements que
l’observateur pourra observer dans l’avenir est de plus en plus réduit. Le rayon physique après
multiplication par le facteur d’échelle sera lui, constant.
Pour conclure ce long développement, nous nous arrêtons avec Gilles CohenTannoudji
sur la seconde notion d’univers observable, la notion intemporelle, et
sa frontière qui est l’horizon des évènements . En laissant donc de coté l’horizon des particules,
retenons en première approximation univers constamment spatialement plat les points suivants :
1.
L’existence d’une phase finale d’accélération exponentielle assure (convergence de l’intégrale) celle d’un
horizon des évènements,
avec un rayon constamment fini.
2. Dans la phase
d’inflation primordiale exponentielle, le rayon de Hubble est
constant. Le rayon de l’horizon des évènements décroit comme l’inverse
du facteur d’échelle en valeur de distance comobile, et reste constant
en valeur de distance physique.
3. Dans les phases
dominées par le rayonnement ou la matière , avec une expansion en lois de puissance “modérées” ( exposant n positif mais inférieur à
1), le rayon de Hubble croît comme le facteur d’échelle à la puissance 1/n . Le rayon de l’horizon
des évènements décroit, en distance comobile comme en distance
physique. Cette décroissance est de l’ordre de celle de l’opposé du
facteur d’échelle élevé à la puissance 1/n1
en distance comobile, et de celle de l’opposé
du facteur d’échelle à la puissance 1/n en distance physique.
4. Dans la phase
finale dominée par la constante cosmologique, on revient au cas exponentiel. le rayon de Hubble se stabilise. Le rayon de l’horizon des
évènements se remet à décroitre comme l’inverse du facteur d’échelle en distance comobile et se stabilise en distance physique.

Le point de vue de Thanu Padmanabhan
La
réflexion de Gilles CohenTannoudji part d’idées présentées par
l’astrophysicien Thanu Padmanabhan, bien connu dans les milieux de la
cosmologie. Notre conférencier cite en particulier trois articles arXiv de ce scientifique, Emergent
perspective of Gravity and dark Energy , Gravity and is thermodynamics , et enfin Exploring the nature of gravity.
Ces
articles sont difficiles car ils constituent une construction
progressive où plusieurs idées, parfois relativement indépendantes, sont
successivement introduites et développées. C’est peut être dans le
dernier cité par Gilles CohenTannoudji (Exploring the nature of
gravity) que l’ont peut suivre le mieux le cheminement de son
raisonnement.
Quoi
qu’il en soit, Padmanabhan se pose la question des principes permettant
de dériver les équations d’Einstein liant la géométrie et le contenu
matériel de l’univers. La manière “classique” est de considérer une
grandeur calculée sur la totalité de l’espace temps (une intégrale).
Cette grandeur a la dimension physique d’une action (produit d’une
énergie et d’un temps), et dépend, entre autres, du champ métrique,
c.a.d. de la valeur du
tenseur métrique sur chaque évènement.
On
calcule alors la manière dont cette action varie lorsqu’on modifie
infinitésimalement le champ métrique, puis on recherche les conditions
pour que cette variation de l’action soit nulle (recherche d’un extrémum
de l’action).
Ces conditions fournissent les équations d’Einstein.
Cette action est la somme de deux parts
1. Une
part purement géométrique, intégrale d’un
“lagrangien” égal sur chaque évènement à la différence entre la courbure
scalaire locale de l’espace temps et le double de la constante
cosmologique ; notons que celle ci est introduite à priori,
explicitement, dès le départ des calculs ; on ne s’étonnera pas qu’elle
se retrouve telle quelle dans leur résultat.
2. Une part relative au contenu matériel, intégrale du
lagrangien des champs d’énergie.
Padmanabhan
conserve cette méthode “variationnelle” recherche de l’extrémum d’une
fonctionnelle mais la grandeur à laquelle il l’applique n’est plus la
même : c’est une grandeur “thermodynamique”, une “densité de chaleur”
(“heat density”). Comme dans la dérivation classique, la grandeur mise
en avant par Padmanabhan se décompose en deux parts, une part liée au
contenu matériel et à ses mouvements, et une part “géométrique”,
“heat density of the atoms of space”. Une bonne part de ses papiers consiste à justifier ce choix et ces qualifications.
Par ailleurs, autre différence, les résultats du calcul de l’extrémum
ne sont plus tout à fait les mêmes : ce ne sont plus directement les équations d’Einstein, mais des équations dont ces dernières peuvent se déduire. Dans cette dernière étape,
la constante cosmologique, qui n’a jusqu’alors pas été introduite, émerge en tant que constante
d’intégration.
Enfin,
dernière différence notable, le champ dont les variations
infinitésimales sont à la base du calcul d’extrémum n’est pas le champ
métrique : la métrique n’est pas “une variable dynamique”
Essayons maintenant d’entrer plus avant dans ces développements ;
La recherche d’une invariance
La
dynamique d’un système matériel, déterminée par son lagrangien, reste
inchangée lorsqu’on modifie ce lagrangien en y ajoutant une constante quelconque, c’est
à
dire une valeur indépendante des variables de positions, de vitesses,
… mobilisées. Cela revient à considérer que l’énergie représentée par
le lagrangien est définie à une constante près, ou encore que le “niveau
zéro” de cette énergie peut être fixé arbitrairement.
Padmanabhan
fait remarquer que les équations d’Einstein, reliant le contenu
matériel de l’univers à sa géométrie ne respectent pas une telle
invariance : dans leur dérivation à partir de la recherche d’un extrémum
d’action avec la métrique comme variable dynamique, ajouter une
constante ᵤ
au lagrangien du contenu matériel revient à modifier la constante cosmologique (qui passe ainsi de
L à
L k L), donc à
modifier la géométrie
de l’espacetemps solution de cette recherche d’extrémum. Exprimé sur
le tenseur d’énergieimpulsion, un tel ajout équivaut à la
transformation
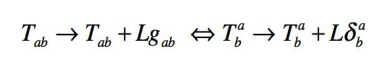
Pour
retrouver l’invariance, Padmanabhan réécrit les équations d’Einstein
sans constante cosmologique en multipliant les termes gauche et droite
par une certaine expression vectorielle ; ainsi :
![]()
Où l est un vecteur attaché à chaque
évènement. Lorsque ce vecteur est un vecteur nul, c’est à dire lorsque
![]()
les équations réécrites sont effectivement invariantes dans la transformation précitée.
A
partir de là, deux questions doivent être résolues : l’interprétation
des termes réécrits, et la dérivation de leur relation à partir d’une
recherche d’extrémum.
La recherche d’une interprétation thermodynamique pour le terme matériel
La
réécriture proposée ne vient pas de nulle part ! Padmanabhan rappelle
d’abord que dans un univers homogène et isotrope, l’expression
tensorielle matériel (terme droit de l’équation) s’écrit Sous réserve d’une certaine normalisation du vecteur l) :
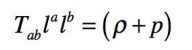
Où r est la densité
et p la pression du fluide parfait emplissant l’espace au temps cosmique t de l’évènement
considéré. La relation de GibbsDuhem (r
+ p = Ts) , avec s densité d’entropie permet alors d’interpréter l’expression tensorielle H m (l) comme la densité
de chaleur présente au sein du fluide à cet instant.
C’est
sur cette équation que Gilles CohenTannoudji s’est appuyé dans son
exposé, pour présenter une dérivation thermodynamique des équations de
Friedmann Lemaître. Mais le développement de Padmanabhan a pour objectif
la dérivation des équations d’Einstein; il lui faut donner une
interprétation générale de la grandeur Hm (x,l) définie
pour tout évènement x et tout vecteur nul l par :
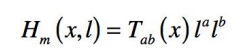
Pour se faire, Padmanabhan mobilise la notion de surface nulle. Une telle surface est un faisceau x(ε;λ) de géodésiques
nulles, c.a.d du genre lumière. A tout évènement
x de la surface il associe le vecteur nul l = dx/dλ , (Ce vecteur l est un vecteur tangent à
la géodésique sur l’évènement
x. Les propriétés des surfaces nulles font que l est orthogonal (dans la métrique
de l’espace temps) au plan tangent en x à ladite surface, lequel plan tangent est du genre espace). et par là
même une valeur de Hm(x,l) .
La clé de l’interprétation de la grandeur Hm (x,l) ainsi définie
fait appel à un observateur (local) particulier, par exemple un “observateur de Rindler ” (Un observateur de Rindler est un observateur se déplaçant
avec une accélération constante relativement à un référentiel inertiel.), percevant la surface nulle considérée comme un horizon d’évènements.
Par
construction, un signal émis à proximité de l’horizon mettra un très
long temps, “quasi infini”, pour parvenir à cet observateur. Un flot
d’énergie traversant la surface nulle est perçu comme tel par un
observateur inertiel. Ce n’est pas le cas pour l’observateur ayant cette
surface comme horizon : pour ce dernier les mouvements sont pour ainsi
dire “figés” et de chaleur” emmagasinée à l’intérieur de cette surface.
Un calcul permet
alors de comprendre Hm (x,l) comme une densité de chaleur présente
sur l’évènement x de l’horizon
considéré . (Donc susceptible d’être affecté d’une certaine température
T. Cette température dépend linéairement de l’accélération caractérisant
l’observateur de Rindler dans le repère inertiel (cf travaux de Unruh,
Gibbons, Hawking,...). Quelles sont les implications de cette
dépendance, et comment les comprendre ? A noter que dans l’exposé de
Gilles CohenTannoudj, la température attribuée à l’horizon des
évènements dans un univers de FriedmannLemaître est fournie par une
formule similaire, dans
laquelle le taux d’expansion H joue le rôle de l’accélération.)
Cette
densité est le rapport entre une quantité de chaleur et l’élément 3D de
“volume” de l’horizon. La structure 3D de la surface nulle croise la
dimension du paramètre affine λ avec les deux dimensions des sections λ
constant.
C’est la raison pour laquelle Hm (x,l) est également appelée densité de chaleur par unité
d’aire et unité de temps
La recherche d’une interprétation thermodynamique pour le terme géométrique
Parallèlement à la définition et à l’interprétation thermodynamique de la grandeur Hm (x,l) liée au contenu matériel par le biais du tenseur EnergieImpulsion, Padmanabhan définit et
donne une interprétation thermodynamique à une seconde grandeur Hg (x,l) liée à la géométrie de l’espacetemps, et donc à la
gravité, par le biais du tenseur d’Einstein.
Pour
se faire il considère l’espacetemps comme un “fluide” composé
d’éléments discrets des “atomes”, dont il calcule la fonction de
distribution
Avant de développer cette démarche, donnons en le résultat.
La grandeur Hg (x,l) autour d’un certain évènement x associé
à un vecteur nul l s’exprime par :
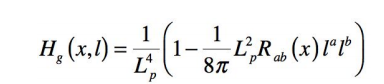
Le tenseur R(x) est le tenseur de Ricci sur l’évènement
x, et L p est la longueur de Planck. Hg (x,l) est interprété
comme une densité de chaleur du fluide formé “d’atomes
d’espacetemps” au point (x,l) d’un certain “espace de phase”.
L’idée est d’évaluer
une densité de nombre d’atomes, donc de degrés de liberté, en
conséquence une densité d’entropie, puis, en s’appuyant sur une valeur
de température, de transcrire en densité de chaleur.
Pour ce faire, Padmanabhan pose un principe de discrétisation de l’espacetemps
: l’intervalle entre deux évènements ne peut être nul ;il formalise cette contrainte de la manière suivante :
1. il substitut à l’intervalle géodésique classique
σ²(x’,x) entre deux évènements
un nouvel interval S[ σ²(x’,x) ] qui tend vers une limite finie L₀
² lorsque l’intervalle classique tend vers 0. Cette limite L₀
est supposée être de l’ordre
de la longueur de Planck ; la relation entre S[ σ² ] et σ² proposée
à titre d’exemple est simple : S[ σ²
] = σ² + L₀
²
2. cette substitution lui permet d’introduire un
espacetemps renormalisé, doté
d’une
“qmétrique ” ; cette qmétrique étend à cet espace temps renormalisé la
métrique de l’espacetemps initial : c’est une quantité tensorielle dont
les seize composantes sont des fonctions du couple d’évènements x’,x
, dont les valeurs dépendent de L₀
² : elle est construite de manière à tendre vers la métrique classique lorsque L₀
² →0
3. toute grandeur calculée sur un évènement
x quelconque à partir de la métrique
classique et de ses dérivées, peut être ainsi “renormalisée” pour le
même évènement à partir de la
qmétrique : on substitue la qmétrique à la métrique dans l’expression
classique de cette grandeur, puis on passe à la limite en faisant tendre
x’ vers x, L₀
² restant fixée à la valeur choisie.
Dans l’espacetemps classique un évènement est ponctuel, et n’a donc ni surface ni volume.
Si
dans l’espacetemps renormalisé l’intervalle entre deux évènements ne
peut être nul, les évènements ne sont plus vraiment ponctuels ;on peut
donc espérer pouvoir leur attribuer un volume et/ou une aire non nulle.
Padmanabhan considère donc une région de l’espacetemps autour d’un évènement x, région délimitée par une surface dont les évènements x’ sont tous
à une distance géodésique σ(x,x’)
= σ donnée ;puis
il étudie ce que devient cette région
dans l’espacetemps renormalisé, du point de vue de la mesure de son
volume et de l’aire de la surface qui la délimite, lorsque
σ→0.
Mais la surface “equigéodésique”
des évènements x’
se compose de deux parts disjointes : la part pour laquelle l’intervalle x,x’
est du genre temps, et celle pour laquelle cet intervalle est du genre
espace. Ces deux parts n’ont pas la même forme puisque la première
s’apparente à une sphère, et la seconde à un hyperboloïde.
Lorsque σ→0, la première
part “s’évanouit”
sur l’évènement x, alors que la seconde a pour limite la surface nulle formée par les cônes de lumière passé et futur de l’évènement x.
Padmanabhan analyse ce qui se passe lorsque (x,x’) est du genre temps ;
il transpose ensuite les
formules obtenues au second cas, évidemment plus intéressant puisqu’on y
retrouve la notion de surface nulle et les vecteurs nuls associés, déjà
en œuvre dans Hm (x,l)
Le volume d’une région R(x,σ) et l’aire de la surface
S(x,σ) qui la délimite s’identifient
respectivement à une intégrale d’éléments infinitésimaux de volume √g dσ’ dθ
dφ dψ et d’aire √h
dθ dφ dψ
, g et h étant les déterminants des matrices représentant les métriques concernées dans le
système de coordonnées choisi . Ces déterminants sont évalués sur chaque évènement y en jeu ;leur valeur dépend de la distance géodésique
σ’ séparant cet évènement y de l’évènement
de référence x ;
elle dépend aussi d’une correction de courbure dont l’expression fait intervenir un vecteur n normal
à la surface S(x,σ’) sur l’évènement y
Le calcul mené par Padmanabhan examine ce que deviennent √g et √h
dans l’espacetemps renormalisé, en appliquant la procédure décrite plus
haut : substitution de la qmétrique à la métrique classique, puis
passage à la limite en faisant tendre σ vers 0 dans les expressions
obtenues sans changer l’intervalle L₀ .
Et arrive alors une surprise : √g devient nul mais pas √h
!
Si l’on interprète les résultats
du passage à la limite lorsque σ→0,
comme, après intégration, le volume et l’aire de l’évènement
x , on doit en conclure que ce volume est bien nul mais que son “aire” ne l’est pas.
Pour
passer d’une telle “aire” à un “nombre d’atomes d’espace”, où ce qui
revient au même, passer à une mesure sans dimension, il ne reste plus
qu’à attribuer à ces atomes une aire intrinsèque.
Padmanabhan adopte la solution la plus simple, et attribue à ces atomes l’aire d’une sphère 3D de rayon L₀ .
Avec un tel choix, la densité f(x,n) du nombre d’atomes
attachés à l’évènement x sur la direction donnée par le vecteur n du genre temps, a pour expression
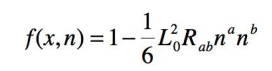
Suite, à venir ….(peut être !)
POUR ALLER PLUS LOIN :
Exploring the Nature of Gravity par Thanu Padmanabhan, article cite plusieurs fois par GCT.
Évolution de l’Univers le modèle standard de la cosmologie par Jean-Christophe Hamilton APC
Jean Pierre Martin SAF Président de la Commission de Cosmologie
Abonnez-vous gratuitement aux astronews du site en envoyant votre e-mail.
PROCHAINES RÉUNIONS DE LA COMMISSION DE COSMOLOGIE :
Notez dès à présent les dates des prochaines réunions : toujours à 15H au siège 3 rue Beethoven P16
Nous sommes satisfaits de la nouvelle réorganisation de la salle. Merci d’avance de votre aide.
· Samedi 28 Mai 2016 à 15H000 nous recevrons Luc
Blanchet qui nous parlera d’ondes gravitationnelles
Pour les suivantes ; rentrée de septembre : sujet à déterminer, merci pour vos propositions
Notez dès à présent la date de la journée des commissions de la SAF : le samedi 21 Mai 2016
à l’École des Mines, on apprécierait votre présence pour cette journée
que l’on essaie de renouveler dans sa structure. (Invité
surprise !!!)
Marquez ces dates dans vos agendas