Chapitre 7
Thermodynamique
de l’univers primordial
7-1 Introduction
Nous allons maintenant nous intéresser aux conséquences du
modèle de Big bang chaud, basé sur la métrique FLRW
qui stipule que l’univers a débuté par un état bien plus chaud et dense que ce
que nous observons aujourd’hui. En particulier, nous verrons comment nous
pouvons suivre l’évolution des densités
des différents types de particules et de rayonnement tout au long de l’histoire
de l’univers primordial. Ceci nous permettra de faire certaines prédictions
pour les abondances des éléments légers,
des photons et des neutrinos que nous
devrions observer aujourd’hui. L’accord entre les calculs et les observations
de concentration d’hélium, de deutérium,
et de lithium est une des pierres angulaires du scénario de Big bang.
Comme d’habitude pour simplifier la notation nous
posons :
c = h = 1 ( 7.1)
ce qui signifie , comme nous l’avons vu en section 2.4.1,
que toutes les grandeurs dimensionnées peuvent être exprimées en terme de masse-énergie , eV
( ou plutôt MeV et GeV). Pour obtenir ces grandeurs en unités SI,
on doit réintroduire les puissances appropriées de h et c
dans l’expression finale. Les puissances
à introduire sont en général déterminées par l’analyse dimensionnelle
(section 2 .4.2).
Par exemple, pour écrire la constante de la gravitation en
termes de masse de Planck, regardons la valeur dimensionnée :
G = 6.672 . 10-11 m3.
kg-1.s-² (7.2)
Ensuite nous l’écrivons sous forme de produit h
α c β mpl γ,
où les constantes α,β,γ peuvent être déterminées en imposant que la
combinaison ait la même dimension que G. Ceci définit une masse de Planck telle
que :
G = h.c/mpl² (7.3)
De valeur numérique :
mpl
= (h.c/G )1/2 = 1.221
. 109 GeV/c² (7.4)
Soit en posant c = 1
mpl
= 1.221 . 109 GeV (7.5)
C’est une masse énorme, nous verrons que la particule
élémentaire la plus lourde connue aujourd’hui est le quark t de
masse 175 GeV « seulement »
Lorsque nous parlons de la thermodynamique de l’univers
primordial, il est pratique de mesurer la température en unités d’énergie où de masse, ce qui
signifie que nous posons la constante de Boltzmann kB
= 1 (Dans cette échelle 1 MeV = 1.165.
1010 K).
Nous ne considérerons que la métrique de Friedmann Lemaître
Robertson Walker, ( FLRW) ,
dont l’équation de Friedmann (4 .16) dérive de la composante temporelle de
l’équation d’Einstein :
H²(t)+ k/a² = 8 πGρ/3 (
7.6)
Où comme d’habitude, le paramètre de Hubble H = H(t) = a’ (t)/a(t), avec H
aujourd’hui = H0 = h.100km/s -1.Mpc-1,
et selon les observations récentes h = 0,73.
Introduisons
Ω=ρ/ρ crit (7.7)
Où la densité critique ( qui
correspond à k=0) est donnée par
ρcrit
= 3H²/8πG (7.8)
Aujourd’hui la densité critique correspond à
ρ0crit
= 1,9h².10-29 g .cm3 (7.9)
Aujourd’hui, les observations semblent indiquer une
contribution de matière de 0.3 et d’énergie sombre de 0.7 à Ω. Nous verrons que le modèle
cosmologique avec inflation prédit Ω
= 1, ce qui et conforme aux observations. Il y a différentes contributions
à Ω, telles qu’indiquées (ainsi qu’une
contribution radiative aujourd’hui négligeable). Dans ce chapitre nous
introduirons Ωk , densité de courbure déduit de k. Dans
l’univers primordial le facteur de courbure est moins important. On peut le
montrer comme suit. Les équations du mouvement pour la matière dans l’univers
sont régies par l’annulation de la divergence covariante du tenseur énergie
impulsion.
Tαβ ;β = 0 (7.10)
Pour la métrique FLRW cela donne :
d/dt(ρ.a3) = -p.d/dt(a3) (7.11)
Qui montre que la variation d’énergie dans un élément de
volume co-mobile est égale à la pression multipliée par le changement de volume
(avec le signe-).
Nous avons vu au en section 4.2) que cela peut
s’écrire :
a3
dp/dt = d/dt[a3 (ρ +p)] (7.12)
Qui comme nous le verrons peut être interprétée comme la loi
de conservation de l’entropie dans un volume a3(t). Pour le rayonnement où p = ρ/3, l’équation
(7.11) donne ρ proportionnel
à a-4. Notons que les particules «
relativistes » dont l’énergie cinétique est supérieure à l’énergie au
repos, se comportent comme du rayonnement.
Si c’est la matière qui domine, ρ
est proportionnel à a-3. Dans tous les cas,
nous verrons que pour a petit, le terme
de courbure k/a² est beaucoup moins important que la densité
d’énergie ρ. De plus la
constante cosmologique, dont la contribution aujourd’hui est importante était
complètement négligeable à cette époque (sauf pendant l’hypothétique période
d’inflation où sa valeur est supposée colossale).
L’équation de Friedmann pour l’univers primordial se
simplifie alors en :
H²(t) = 8 πG ρ/3 (7.13)
Où en première approximation seules les espèces relativistes
contribuent de manière appréciable (Nous quantifierons cette assertion dans la
suite). Remarquons que le paramètre de Hubble H(t)
= a’(t)/a(t) a les dimensions de
l’inverse d’un temps. Dans nos unités cela lui confère les dimensions d’une
masse. En section (4.5.1) nous avons vu que l’ordre de grandeur de l’âge de
l’univers [le facteur naturel d’échelle] est de 1/H, du
moins si la loi d’échelle est en puissance de t.
Nous voulons maintenant traiter la thermodynamique d’un
univers en expansion. La première question à se poser est : est ce bien
raisonnable et possible ?
Un point crucial est la compréhension au niveau
microscopique, de la thermodynamique, en terme de mécanique statistique portant
sur un grand nombre de particules élémentaires (quanta). En général,
l’équilibre statistique requiert un nombre incessant d’interactions entre les
constituants du système.
Si la fréquence d’interactions est suffisante, alors la
description de l’évolution de l’univers
à travers une séquence d’états en équilibre thermique est bonne et nous pouvons
utiliser les paramètres thermodynamiques, la température T, la
pression p, la densité d’entropie s, et d’autres à
chaque instant t pour décrire l’état de l’univers.
Si les constituants de l’univers de densité numériques n
et de vitesses relatives v, interagissent par diffusion élastique
de section efficace σ, le taux Г
d’interaction par particule est donné par Г
= n.σ.v. La condition d’équilibre est que le taux d’interaction
doit être bien plus grand que le taux d’expansion de l’univers.
Г >> H (7.14)
Typiquement, la densité numérique des particules, décroît
plus rapidement avec la température que le paramètre de Hubble. Cela implique
que certaines particules vont quitter l’équilibre thermique à certains instants
de l’histoire. La densité numérique va être gelée à une valeur particulière qui
ne va évoluer qu’à travers la dilution liée à l’expansion de l’univers.
Comme nous le verrons ce passage hors équilibre des
particules est un mécanisme important qui peut expliquer en grande partie la
teneur en particules de l’univers observé aujourd’hui.
7-2 Equilibre thermodynamique
Nous travaillons dans l’approximation, d’un gaz dilué
interagissant faiblement, où la fonction de distribution fi(p)
pour les particules d’espèce i est donnée par :

où ![]() est l’énergie , µi
le potentiel chimique et T est la température ( rappel : kB =1).
est l’énergie , µi
le potentiel chimique et T est la température ( rappel : kB =1).
Le signe « moins » est pour les particules qui
suivent la statistique de Bose Einstein (bosons) et le signe « plus »
est pour les particules qui suivent le principe d’exclusion de Pauli
(statistique de Fermi-Dirac : fermions). On
admet en général que le potentiel chimique peut être négligé dans l’univers
primordial.
Un autre paramètre important est le nombre gi de
degrés internes de liberté de la particule,
qui s’ajoutent indépendamment aux densités numériques, d’énergie, à la
pression, etc…
[En effet, on va considérer in fine, le mélange de
particules différentes comme constituant un seul gaz à «
l’équilibre » , chaque degré de liberté des
particules étant considéré comme une particule différente. La démarche va
consister à calculer, les lois pour une espèce i et ensuite à combiner toutes
les espèces participant à un moment donné à l’équilibre thermique, avec leurs
degrés de libertés, pour calculer les lois globales liées au mélange qui
participe à l’équilibre, voir ce qui se passe quand une espèce quitte
l’équilibre etc…]
Dans le chapitre précédent nous avons énuméré les degrés de
liberté des particules du modèle standard. Le photon a deux états de
polarisation donc gγ
= 2. Les neutrinos n’ont qu’un état de polarisation, donc gν = 1, les
électrons et les muons ont ge,µ = 2 ( et même nombre pour les anti particules).
Fort de ces définitions nous pouvons écrire la densité numérique d’une espèce i :

[Le facteur (2π)3
vient du fait que la taille de la maille de référence du réseau d’
impulsions, dans l’espace
« dual » associés à une boite de dimension L, donc de volume L3
vaut L/2π .]
et la densité d’énergie

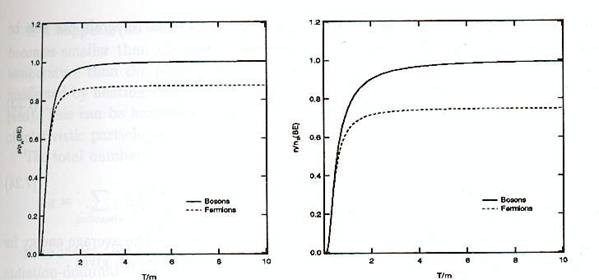
Figure 7.1 : Densité numérique (b) et densité d’énergie
(a) pour les fermions et les bosons (qui participent à l'équilibre thermique),
fonction de T/m. Les grandeurs ont été normalisées à l’expression relativiste
pour les bosons : nR
(BE) = ζ(3)giT3/π² et ρR
(BE) = π ²giT4/30, respectivement.
Et sa pression
![]()
Comme les fonctions de distribution ne dépendent que de |
p| ,
nous prenons d3p à p²dpdΩ
(avec p = |p| ) où l’intégrale sur dΩ
donne juste un facteur 4 π [ on fait l’intégrale de
« volume » en coordonnées « sphériques »]. En
différentiant la relation (voir équation
2.44) Ei² = p² +mi²
nous obtenons p.dp = EidEi,
de sorte que :
![]()
Les expressions résultantes pour n(T)
et ρ (T) sont
montrées sur la figure 7.1 (a) et (b). Remarquons deux choses, premièrement pour
T/m petit, quand les particules ne sont pas relativistes, il n’y
a pas de différence entre les bosons et les fermions, et deuxièmement les
densités chutent très rapidement
(exponentiellement) lorsque la température décroît.
[Remarquons également que le nombre « n »
dépend de la température, ce qui veut dire que la densité de particules, n’est
pas invariante, elle dépend de la température, ce qui est un résultat bien
connu de la théorie des champs]
Dans la limite non relativiste T/m << 1,
on peut résoudre les intégrales analytiquement, ce qui donne les résultats
suivants (pour les particules de
statistiques Fermi Dirac et Bose
Einstein)

[E ] = m + 3T/2 dans
le cas non relativiste. Si nous réintroduisons les unités, cela s’écrit :
mc² + 3kB
T/2. On retrouve le résultat connu que hors de son énergie au repos,
l’énergie thermique moyenne d’une particule ponctuelle est + 3kB
T/2)
Dans l’approximation ultra relativiste, T/m >> 1,
les intégrales peuvent aussi être résolues analytiquement et donnent :
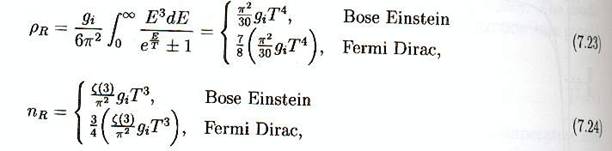
Où ζ est la
fonction zéta de Riemann ζ
(3) = 1.20206. L’énergie moyenne d’une particule relativiste s’obtient
par le rapport ρ/n , ce qui donne :
![]()
et
![]()
Pour les photons de masse m =0 et g = 2,
l’expression ργ=
k.T4 est la fameuse loi de Stefan Boltzmann de
l’émission radiative du corps noir.
Attaquons nous maintenant au calcul de la contribution
totale à la densité numérique et d’énergie de toutes les sortes de particules
dans l’univers primordial. Comme nous avons vu que la densité numérique et d’énergie des espèces non relativistes est
exponentiellement atténuée comparée aux espèces relativistes, souvent on fait
l’approximation que seulement les particules relativistes sont à l’équilibre à
ces températures. Ceci signifie que la
densité d’énergie va avoir la forme de la loi de Stefan Boltzmann.

Où le facteur de dégénération effectif geff
(T) représente le nombre total de degrés de libertés internes (spin,
couleur,etc..) des
particules relativistes et à l’équilibre thermique à la température T
( celles dont mi << T). L’expression pour geff (T) contient
aussi le facteur 7/8 pour les fermions qui intervient dans la
formule (7.23) pour ρ(T)
( voir équation 7.30) ci dessous.
Il est instructif de calculer geff
(T) pour une température disons de 1 TeV
quand toutes les particules du modèle standard sont relativistes et à
l’équilibre thermique. Le nombre total de degrés de liberté interne des
fermions est de 90 et pour les bosons de jauge et de Higgs 28, alors geff
vaut :
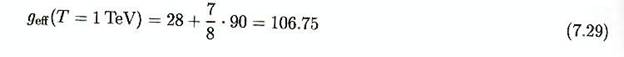
S’il arrive (comme nous le verrons pour les neutrinos) que
le taux d’interaction devient plus petit que le taux d’expansion, alors ces
particules vont avoir une température inférieure à celle des photons, bien
qu’étant toujours relativistes (Les neutrinos seront insensibles au réchauffement qui affectera les photons car il se produira
après que ces neutrinos se seront découplés). On peut en tenir compte en
introduisant une température spécifique Ti
pour chaque sorte de particule relativiste, qui peut être inclus dans le gi
effectif.
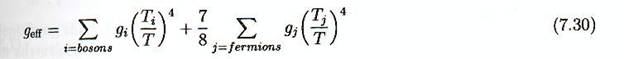
Si nous insérons cette expression dans l’équation de
Friedmann (7.13) nous obtenons pour la
période radiative de l’univers primordial :
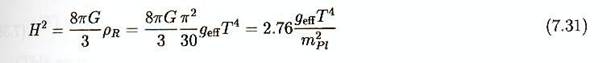
soit

Ceci est une des formules les plus importantes de la
physique de l’univers primordial. Des relations entre le facteur d’échelle a et
le temps que nous avons établi en section (4.2) nous obtenons (voir équation
4.28)
![]()
Pour une équation d’état p = ρ/3. Pour
l’époque (ultérieure) dominée par la matière, p =0, on trouve
![]()
Donc pour l’époque radiative
![]()
et la relation temps- température
devient
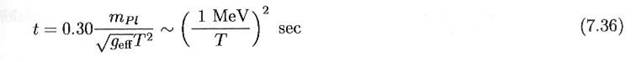
C’est une formule qu’il convient de mémoriser, valide pour
les températures cruciales, autour de 1 MeV,
où l’essentiel de la nucléosynthèse et le découplage du neutrino se sont
produits, comme nous le verrons.
7.3 Entropie
Déterminer quelles particules sont en équilibre thermique à
une température donnée, ainsi nous pourrons calculer geff (T).
Considérons d’abord quelques relations thermodynamiques de base ; En
particulier, nous allons montrer que dans le cas de l’équilibre thermique,
l’entropie dans un volume a3 (t) est conservée.
L’entropie S (V,T) a été
introduite comme une des équations clés
de la thermodynamique par sa
variation.
![]()
Identifions les
fonctions coefficients
multipliant dT
et dV
de cette expression avec ceux de la forme générale d’une différentielle.
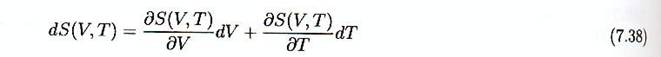
Nous trouvons

Et

Egalons les dérivées mixtes

Cela donne
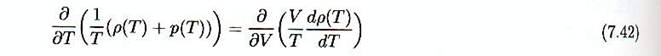
Ce qui peut être simplifié en :

Ce qui peut être déduit également directement de des
équations (7.17) et (7.18). En reportant cela dans (7.37) on obtient :
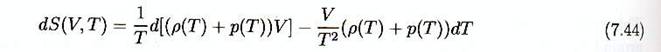
Qu’on peut immédiatement intégrer pour montrer que
l’entropie S(V,T) est, à une constante d’intégration près ,
donnée par :

Rappelons nous l’équation (7.12)

Combinée avec (7.43), on peut l’écrire

En identifiant le volume V à a3(t)
et en comparant avec (7.45), nous trouvons finalement la conservation de
l’entropie dans le volume a3(t)
ainsi que nous l’avions annoncé. Quelquefois il est plus judicieux de
travailler avec la densité d’entropie s(T)
plutôt qu’avec l’entropie totale s(V,T) dans le volume V.
La définition est alors

(Cette partie a été plutôt formelle. L’important est de
mémoriser les expressions (7.45) pour l’entropie, (7.48) pour la densité
d’entropie et l ‘équation de conservation (7.47)
Dans l’univers primordial, et la densité d’énergie ρ, et la pression p
étaient dominées par les particules relativistes avec l’équation d’état p
= ρ/3.
En utilisant (7.48) et les expressions relativistes (7.27,7.28) pour la
densité d’énergie et la pression, nous trouvons finalement pour la densité
d’entropie s :

Où gseff
est défini de façon similaire à geff :
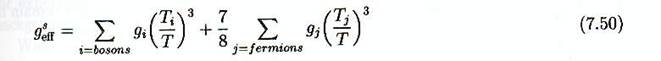
Comme s et nγ
varient tous deux comme T3, il y une relation simple
entre eux.
![]()
On trouve

Considérons maintenant la question du découplage des
neutrinos de l’équilibre thermique dans
l’univers primordial. Comme nous l’avons indiqué, les particules interagissant
faiblement comme les neutrinos, se découplent en dessous d’une température Tdec quand le taux d’interaction
entre les particules n’est plus assez rapide
pour lutter contre l’expansion de Hubble de l’espace. Les médiateurs
des interactions faibles sont les
particules W et Z qui sont massives mw = 80 GeV
et mz = 91 GeV. A
des températures bien inférieures à 80-90 GeV
les bosons W et Z sont virtuels de sorte que leurs propagateurs sont en 1/m²w
(voir chapitre 6.10.1)
Nous avons montré au chapitre 6.10.1 que la section efficace
pour les interactions faibles est proportionnelle à α²s /m4w
Pour des neutrinos relativistes (compte tenu de leur très
faible masse présumée, c’est toujours le cas),
en général la condition est mν
<< T et pour les leptons
relativistes chargés, une réaction typique maintenant l’équilibre
thermique telle que νe
+ e+ à νµ + µ+
va suivre un taux σweak
≈ α²T²/m4w. Ceci est dû au fait que s
dépend du carré de d’énergie des particules en réaction, et l’énergie moyenne
est proportionnelle à T. Le taux d’interaction Г = σ|v|n, (comme |v|
=c=1 et n ≈ T3), vaut
alors :

Nous devons comparer ceci au taux d’expansion H.
Comme nous l’avons vu (1.32) H ≈ T²/mpl,
donc le rapport devient :
Le découplage se produit quand ce rapport tombe sous
l’unité, soit

Qu’arrive t’il quand les neutrinos se sont découplés. Tous
les neutrinos vont se comporter en particules libres suivant l’expansion de
Hubble. Ce qui implique que leurs énergies vont être
réduites, comme pour les photons par le facteur d’expansion a/adec. Il vont rester dans une
distribution ( Fermi Dirac) d’équilibre thermique de
température :
![]()
Si nous nous appliquons la conservation de l’entropie à
l’équilibre thermique
![]()
Nous voyons que :
![]()
Donc même après son découplage, la distribution de neutrino
va être la même que s’il était resté à l’équilibre thermique (distribution
gelée) tant que gseff
ne change pas. Cependant gseff
va changer quand les électrons et les positons vont cesser d’être relativistes et vont s’annihiler par la réaction e+e-
à
γγ.
Cela se produit à une température de 1 MeV , car en dessous la réaction inverse γγ.à e+e-
, n’est plus cinématiquement possible ( la masse au repos d’une paire positon
électron est de 1.02 MeV). Calculons le nombre
de degrés de libertés avant et après l’annihilation e+e-
.Les neutrinos sont déjà découplés, donc à une température sensiblement
supérieure à 1 MeV les espèces
relativistes en équilibre thermique sont e+e- et les γ,
ce qui donne (gseff ) avant = 2.2.7/8 + 2 = 11/2 alors qu’en dessous de 1
Mev,
seuls les photons sont en équilibre thermique donnant (gseff ) après =
2.
Comme l’entropie totale des particules à l’équilibre est
conservée :
![]()
Ce qui implique
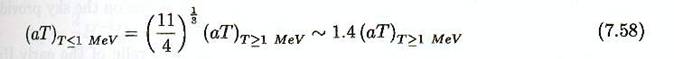
Il y a un transfert d’entropie des particules e+ e- qui se
découplent aux photons, qu’on appelle un « réchauffement » (bien
qu’en fait la température n’augmente pas, simplement elle décroît plus
lentement pour les photons du fait du transfert d’entropie). Par contre, les
neutrinos déjà découplés, ne bénéficient pas du « réchauffement ».
Ils ne font que suivre la loi due à l’expansion de l’univers (aTν)avant
= (aTν)après . On
peut l’interpréter en disant que l’entropie est conservée séparément après le
découplage. Cela implique une différence de température entre les photons et
les neutrinos après le découplage e+e-,
de : 
Comme le RFC ( photons)
a maintenant une température de 2.73K, il doit y avoir un fond de
neutrinos cosmologique ayant un spectre d’énergie de Fermi Dirac de température
Tν = 1.95 K.
Comme des neutrinos d’une énergie aussi faible interagissent très faiblement
avec la matière, c’est un défi extrême pour la physique expérimentale du 21 ième siècle de les détecter directement.
Quelle est l’entropie totale et la densité d’énergie du rayonnement
aujourd’hui ? C’est donné par les contributions des photons et des trois
espèces de neutrinos (νe,νµ, ντ)
soit
![]()
Et
![]()
Pour la densité d’énergie totale du rayonnement ceci
donne :
![]()
Ce qui correspond à une contribution à Ω
= ρ/ρcrit de :
![]()
La densité numérique des photons du RFC vaut :

Pour T = T0 = 2,73 K. Bien que contribuant faiblement à Ω aujourd’hui, le RFC quand il a été émis a
joué un rôle important dans la dynamique de l’univers. L’utilisation la plus
importante du RFC est liée au fait qu’il nous propose un «instantané» de
l’univers à un redshift de 1100
environ. Dans le chapitre 11.2, nous verrons comment des différences minuscules
de température réparties dans toutes les directions du ciel, nous donne des indices sur la manière dont
l’univers s’est formé. Peut il y avoir
d’autres vestiges de l’univers primordial, d’autres types de
rayonnements ? On est en droit de supposer que les gravitons, les
particules de jauge de la gravitation existent. Etant reliées à la gravitation,
l’échelle de masse pour leur interaction
est la masse de Planck, σ grav
~ T²/M4pl
et Г
grav /H ~ T3/m3pl,
ce qui fait que leur température de découplage doit être énorme, T dec ~ mpl
~1019 GeV.
Nous avons vu avant que le nombre de degrés de libertés est
très grand, à très haute température. A l’échelle de Planck, il devait être
encore beaucoup plus grand du fait de la présence de particules lourdes prévues
par la super symétrie et la grande unification.
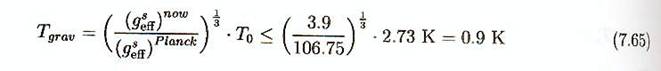
La contribution à la densité d’énergie actuelle est donc,
puisque ρ ~ T4, ρ grav < 0.012
ργ.
Après le découplage des particules relativistes, leur
contribution à la densité d’énergie diminue en 1/a4 ( car ρ = T4 et aT ~ constante ). Pour
la matière non relativiste, cependant la densité d’énergie s’écrit
maintenant :
![]()
Et pour les particules stables ( comme
les baryons) n N ~ 1/a3 ~
T3. Donc, en fait l’univers est devenu dominé par la
matière. Quand cela arriva t’il ? La contribution de la matière à la
densité d’énergie s’écrit maintenant :
![]()
Alors

Avec la notation habituelle pour le facteur de redshift : 1 + z = a0/a .
De même :

En égalant (7.68) et (7.69) on obtient :
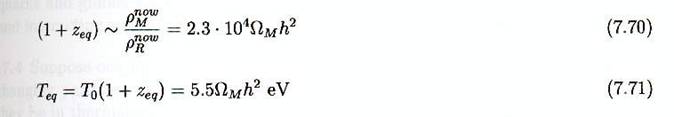
et ( voir exemple 4.5.1, nous
supposons Ω ~ 1)
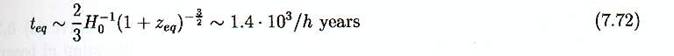
Comme nous l’expliquerons dans le chapitre de formation des
structures, le moment ou la matière a commencé à dominer l’univers est très
important, car c’est seulement à partir de là que les structures ont pu
commencer à croître.
Résumé
- Dans l’univers primordial, le taux d’expansion a dépendu
essentiellement des particules relativistes. La contribution à la densité
d’énergie de ces particules relativistes est
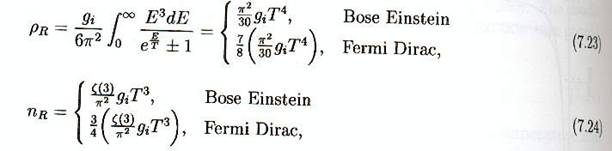
Où

Ici, on a pris en compte la possibilité d’avoir des
températures effectives différentes.
Pour les particules non relativistes on obtient :

- pendant l’ère radiative (les quelques premières centaines
de milliers d’années) le taux d’expansion est donné par :
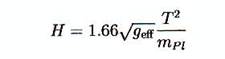
Et la relation entre la température et le temps autour de 1
MeV était :
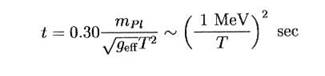
- L’entropie totale S(V,T) dans une région de
l’univers a été conservée pendant les périodes d’équilibre thermique,
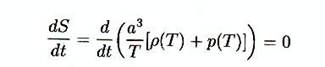
La densité d’entropie est donnée par :
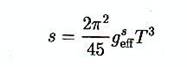
Avec
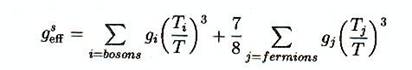
- Les neutrinos se sont découplés à une température
d’environ 4 MeV, mais leurs fonctions
de distribution ont conservé le profil thermique, simplement décalés vers le
rouge par l’expansion cosmique. Mais comme ils étaient déjà découplés au moment
du « réchauffement » quand les électrons et les positrons sont devenus
non relativistes, le fond de neutrinos cosmologique est plus froid que celui
des photons.
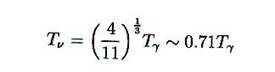
- la contribution du RFC à la densité
d’énergie aujourd’hui n’est que de :
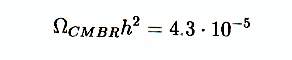
Et la densité
numérique est donnée par la formule (7.64)