Chapitre 6 : Particules et champs

Extrait de « Cosmology and particle astrophysics » par Lars Bergström et Ariel Goobar (traduction, J. Fric qui endosse la responsabilité des erreurs que sa traduction aurait pu introduire)

6-1 Introduction

6-2 Petite revue des particules en physique

6-3 Nombres quantiques

6-4 Degrés de Liberté dans le modèle standard

6-5 Mésons et baryons

6-6 Champs de jauge

6-7 Bosons de jauge massifs et mécanisme de Higgs

6-8 Gluons et gravitons

6-9 Au dela du modèle standard

6-9-1 Supersymetrie

6-10 Un peu de phénoménologie des particules

6-10-1 Estimation de sections efficaces

6-11 Exemple de calculs de sections efficaces

6-11-1 Définition de la section efficace

6-11-2 Interaction des neutrinos

6-11-3Le système photon electron

6-12 Cas des Baryons

6.1 Introduction

Un des sujets les plus passionnants de la cosmologie moderne est sa relation avec la physique des particules. C’est peut être paradoxal, que l’étude des objets les plus petits que nous connaissons, les particules élémentaires, puisse avoir des applications sur les plus grandes structures de l’univers. C’est pourtant le cas, et les relations entre ces deux domaines sont l’objet de nombreux développements scientifiques aujourd’hui. On l’appelle quelquefois, la physique des astroparticules , qui inclut habituellement les rayons cosmiques et l’astrophysique relativiste. Il est de bon ton, aujourd’hui que les astrophysiciens se familiarisent avec les modèles de physique des particules.

Une découverte essentielle du 20 ième siècle, a été l’importance des champs pour la compréhension des intractions fondamentales de la physique. Bien sûr la formulation des théories actuelles est compatible avec avec la relativité et la mécanique quantique. Dans ce livre nous ne présentons pas la théorie relativiste quantique des champs dans toute sa splendeur.. cependant à partir des connaissances acquises dans les chapitres précédents et si vous étudiez l’annexe B ( dynamique relativiste) et l’annexe C ( L’équation de Dirac), dans ce livre , vous aurez acquis une bonne base de connaissances pour aborder la physique des particules appliquées à la cosmologie et à l’astrophysique relativiste. D’autre part, si vous admettez certains résultats sans démonstration, vous pouvez vous contenter des résumés faits à la fin de chaque chapitre et annexe . Repétons que certaines notions comme les champs quantifiés en espace courbe ne sont pas traités dans ce livre.

6.2 Petite revue de la physique des particules

Commençons notre introduction de la physique des particule, en passant en revue, les bases sur les constituants élémentaires de la matière. Selon le modèle standard de la physique des particules, bien établi aujourd’hui, les briques de base de la matière sont les quarks et les leptons, et on en connaît six ( table 6.1 ci dessous).

Charge électrique	Q=0	Q=-1	Q=+2/3	Q=-1/3
Famille 1	ν	e	u	d
Masse	< 5 eV	511 keV	2-8 MeV	5-15 MeV
Famille 2	ν_µ	µ	c	s
Masse	< 170 keV	106 MeV	1-1 .6 GeV	100-300 MeV
Famille 3	ν_τ	τ	t	b
Masse	< 24 MeV	1,78 GeV	170-190 GeV	4.1-4-5 GeV

Notons que comme les quarks sont confinés, la masse du quark n’est pas un paramètre défini de façon unique.

Comme on peut le voir les quarks et les leptons sont groupés naturellement en 3 familles, chacune comportant un lepton électriquement neutre (comme le neutrino ν_e ), un lepton de charge électrique – e ( comme l’électron), un quark de charge + 2/3 e ( comme le quark u), et un quark de charge – 1/3 e ( comme le quark d). Petite curiosité, les quarks ne se manifestent pas à l’état libre. Un proton est constitué de 2 quarks u et d’un quark d, un neutron d’un quark u et de 2 quarks d ( vérifiez que cela donne bien la bonne charge électrique). Les forces qui lient ces quarks ensemble sont si fortes qu’un quark ne peut pas être extrait du système lié. On appelle cela le confinement des quarks. Cependant il existe des méthodes permettant de « secouer » les quarks dans un proton et démontrer ainsi leur existence en tant que constituants individuels des nucléons. Le fait que les quarks fortement liés dans les nucléons ( protons, neutrons) puissent se comporter comme des particules libres pendant des instants très courts comme constaté expérimentalement, est une propriété intriguante des théories modernes appelée liberté asymptotique. La configuration particulière de charges et autres nombres quantiques dans une famille de 2 leptons, et 2 quarks signifie que la théorie va être compatible avec la mécanique quantique. S’il avait manqué une particule, une anomalie aurait été générée et cela aurait eu des conséquences catastrophiques pour la théorie. ( En gros, on n’aurait rien pu calculer, du fait des infinis, qui n’auraient pas pu être renormalisés de façon controlée). C’est la raison pour laquelle le quark Top a été prédit , bien avant qu’il n’ait été finalement découvert expérimentalement en 1995.

Dans la table 6.1, nous avons supprimé quelques nombres quantiques, par exemple chaque quark a 3 degrés de liberté appelés couleurs. La théorie de l’interaction forte , la chromodynamique quantique ( QCD) décrit comment les quarks colorés interagissent. Les leptons et les quarks ont des spins ½ ( en unités de h, la constante de Planck divisée par 2π ). Ce sont des fermions qui obéissent au principe d’exclusion de Pauli. Enfin à chaque particule connue, correspond une antiparticule, de même masse et spin mais de charge électrique opposée. Les neutrinos qui sont neutres , possèdent un autre type de charge, l’hypercharge faible, qui signifie que le neutrino et l’antineutrino sont des particules différentes. Cependant tous les neutrinos semblent avoir un spin « gauche » ( ou une hélicité, qui est la projection du spin dans la direction de la quantité de mouvement). Par symétrie, les antineutrinos sont « droitiers ». C’est ainsi que les neutrinos apparaissent dans le modèle standard. Cependant le domaine des neutrinos est très difficile à étudier du fait de leur faible interaction avec la matière. Il est possible que les neutrinos soient en fait leurs propres antiparticules ( voir annexe C), alors appelée particukes Majorana.

6.3 Nombres quantiques

Le concept de nombre quantique est important en physique des particules. Comme nous le dit la mécanique quantique, le moment angulaire interne s d’une particule est quantifié par pas de 1 ou ½ de h , ce moment angulaire ( spin) est un nombre quantique. D’habitude, l’existence de nombre quantiques conservés reflète l’invariance de la théorie par certaines transformations. Par exemple la conservation du moment angulaire est une conséquence de l’invariance par des rotations de la forme discutée au chapitre 2.3. Un système donné de particules peut avoir un moment angulaire total qui est donné par le spin total de toutes les particules qui le constituent couplé au moment orbital total, conformément aux règles de la mécanique quantique. Une utilisation pratique de cette conservation est une règle générale qui stipule qu’un système qui a un moment angulaire total demi entier ne peut pas dégénérer en système avec un spin total entier.

Il y a d’autres types de transformations, en relation avec les degrés de liberté internes, qui impliquent aussi des conservations de nombres quantiuqes. Un exemple important est la charge électrique, dont la conservation résulte d’une invariance de jauge. ( 2.78). De plus, il y a d’autres « charges » telles que le nombre baryonique, qui semble être conservé avec une très grande précision ( La durée de vie du proton est au moins de 10 ³⁴ ans, d’après les expériences). Là, l’invariance, source de la conservation du nombre baryonique est moins bien comprise ( en fait selon certaines théories, il n’y aurait pas une conservation exacte de ce nombre) , Mais du point de vue phénoménologique, cela peut être considéré comme une loi empirique qui nous indique quelles réactions impliquant des baryons sont permises. La normalisation attribue habituellement un nombre baryonique égal à +1 au proton ( et donc de -1 pour l’antiproton). Alors un quark a un nombre baryonique de +1/3.

De même pour les leptons, il semble qu’il y ades nombres quantiques qui soient conservés au moins approximativement. On attribue à l’électron et au neutrino électronique un nombre leptonique de +1 et de même pour les autres leptons. Il semble que ce nombre leptonique soit conservé avec une bonne approximation. Leur somme , le nombre leptonique total, semble encore mieux conservé. Cependant, répétons qu’il n’y a pas de raison théorique contraignante associée à cette conservation, à la différence de la charge électrique, conséquence d’une invariance de jauge). Il est possible que la conservation du nombre leptonique soit violée à un certain niveau, bien que cela n’ait pas été constaté expérimentalement. Le nombre leptonique individuel n’est probablement pas conservé comme nous le verrons au chapitre 15.

6.4 Degrés de libertés dans le modèle standard

Une manière très utile de considérer les degrés de liberté de spin d’une particule est de considérer qu ‘un état associé à n’importe laquelle des 2s+1 valeurs de m_s, est une particule différente.

Ceci est justifié, car comme nous le verrons au chapitre 7, chacun de ces états contribue indépendamment, par exemple, à la densité d’énergie. La transformation de Lorentz, n’agit pas seulement sur l’espace temps, mais aussi sur les états internes de spin : ils se mélangent.

Ici m_s est la projection du spin sur un axe arbitraire mais fixé. D’ordinaire c’est l’axe z. Cependant , un choix encore meilleur qui permet de mieux traiter les particules sans masse (comme par exemple peut être les neutrinos) est d’utiliser l’hélicité c’est à dire de prendre la direction du mouvement comme axe de projection.

Comptons le nombre g_fam d’états d’hélicité indépendants d’une famille de quark et de leptons. Chaque quark a 3 couleurs et 2 spins, soit 12 états pour les quarks u, d et les antiquarks. Le lepton chargé a 2 états et le neutrino 1. Donc une famille a 15 états, soit 45 pour les trois. Avec les antiparticules cela fait 90 pour les fermions

Au dessus d’une certaine température, de l’ordre de 100-300 MeV, où on suppose que la transition de phase quark-gluon se produit, on subbodore que les quarks et les gluons se comportent comme de particules libres.

6.5 Mésons et Baryons

En dessous de la température de transition de phase QCD, seuls les systèmes non colorés semblent viables. Une manière de faire pour un quark est de se lier avec un antiquark, formant un sytème incolore fortement lié, qu’on appelle un méson ; Les plus légers sont les mésons π , ou pions. La masse du pion ( énergie au repos) est d’environ 140 MeV. Une particule π⁺ est constituée d’un quark u et d’un antiquark d. D’ordinaire, une barre sur le nom de la particule désigne l’antiparticule, donc on écrit π⁺ = ud . Le π^- qui est l’anti^particule du π⁺ est évidemment constitué d’un quark d et d’un antiquark u. Il y a aussi un pion neutre , le π⁰, qui est un mélange quantique de (uu) et (dd). Une autre façon d’obtenir une particule incolore est de prendre 3 quarks, chacun d’une couleur différente ce qui donne, par exemple, un proton ou un neutron.

Donc les particules constituées deq uarks et soumis à l’interaction forte sont de deux types. Soit des baryons constitués de trois quarks comme les nucléons ( le proton, le neutron) ou des mésons constitués d’un quark et d’un antiquark comme le pion. On suppute qu’il existe des particules plus exotiques constituées par exemple de deux quarks et deux antiquarks, mais jusqu’à présent rien n’a été prouvé.

Quand le quark apparut dans les années 60, il offrait une solution à la prolifération des centaines de particules qui avaient été produites dans les accélérateurs. Avec quelques quarks et antiquarks on peur construire un garnd nombre d’états de mésons et de baryons, en utilisant les règles de construction de la mécanique quantique. Les plus importants sont ceux montrés sur la fig 6.1 , qui représentent les états du niveau de base ( qui sont les moins massifs) des mésons et baryons. La classification utilise la symétrie SU(3) de la mécanique quantique qui est fondée sur le principe que les trois quarks légers u,d et s sont sur un pied d’égalité.

Comme la classification en termes d’octets, décuplets et singlets assure une symétrie exacte entre les quarks légers u,d et s, et que cette symétrie est brisée en pratique du fait des masses différentes ( le quark s est plus lourd), il se produit un mélange des états. Par exemple les mésons η0 et η’ sont des mélanges états de singets et de multiplets.

--------------------------------------------------------------------------------------------------------------------

Un méson K⁺ par exemple, est constitué d’un quark u et d’un antiquark s , tands qu’un méson π⁺ est constitué d’un quark u et d’un antiquark d . Les mésons π⁰ et η sont constitués de combinaisons linéaire d’états de (dd), (uu) et (ss) .

Des états supplémentaires sont produit par les exitations des états fondamentaux des mésons et baryons. Par exemple le proton est l’état fondamental d’un système constitué d’une combinaison de de quarks uud , avec les quarks d’un moment angulaire l=0 ( Onde –S) et un spin total 1/2 . Alors, il doit aussi exister un état avec les mêmes constituants mais un spin total de 3/2. En fait une telle particule existe. C’est le baryon Δ+ , qui joue un rôle important en astrophysique. Comme il est très semblable au proton, il est facile d’éxiciter cet état epar collision d’un proton et d’un photon. Nous verrons plus loin, ( chapitre 13.3) que de telles interactions entre des rayons cosmiques ( protons) de très haute énergie et le RFC détermine le libre parcours moyen de tels rayons cosmiques.

Pour les mésons et baryons constitués de quarks c,b et t, la classification en termes de SU(N) n’est pas très utile, car leurs masses au repos sont complètement déterminées par par les masses des quarks. Cependant , le spectroscopie des états peut être interprétée par une simple combinatoire, avec des baryons constitués de trois quarks et des mésons constitués d’un quark et d’un antiquark. Aujourd’hui, nous ne savons pas vraiment pourquoi, il ya trois familles de quarks et de leptons dans la nature. La solution de cette énigme, comme d’autres, devra sans doute attendre une théorie plus complète de toutes les particules et interactions de la nature, incluant la gravitation quantique. Cette théorie aujourd’hui n’est pas faite, les spéculations nous poussent vers une théorie sous jacente appelée M-théorie, qui sous certaines conditions a des solutions qui se présentent sous forme de cordes ou d’objets de dimensions supérieures appelées D-branes . Quand une théorie correcte sera établie, on peut espérer que ce contexte ( comme le nombre de familles) , charges, les masses et autres attributs sera expliqué par des propriétés géométriques dans l’espace comportant un grand nombre de dimensions correspondant au cadre naturel et formel de ces théories .

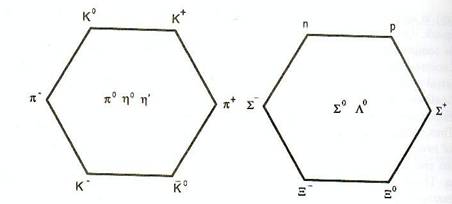
Fig 6.1. L’octet du méson ( sur la gauche) et celui du baryon ( sur la droite) obtenu par la classification SU(3) des états liés des trois quarks

6-6 : Champs de jauge

Introduction

Un Univers qui ne serait constitué que de quarks et de leptons serait ennuyeux et improductif. La dynamique est ce qui décrit leurs interactions, en particulier les états liés dans les hadrons et les atomes. Une conséquence intéressante de la Relativité et de la Mécanique Quantique est que leur interaction peut être décrite en termes d'échange de particules de médiation.

Ce n'est pas difficile à comprendre.

Considérons deux particules chargées, disons un proton et un électron, séparées par une distance finie. Etant chargées elles exercent l'une sur l'autre une action Coulombienne "électronique" . Supposons que nous déplacions légèrement le proton. Le champ environnant va changer , ainsi que son influence sur l'électron. Mais la Relativité Restreinte nous dit que la perturbation ne peut pas se propager plus vite que la lumière ( pas d'action instantanée à distance).

Théorie des champs

La description moderne des forces s'appuie sur la notion de champ, donc la perturbation va moduler le champ entre le proton et l'électron. La mécanique quantique considère ces modulations comme des degrés de liberté dynamiques qui doivent être quantifiés comme les autres. Les excitations minimales ( quanta) du champ sont interprétées comme des particules, et l'interaction entre un proton et un électron est décrit en termes d'échange de ces particules.

Comme les équations de Maxwell nous enseignent que le champ électromagnétique a des solutions ondulatoires, dont la lumière est un exemple, nous identifierons ces particules, associées au quanta du champ, aux photons qu'Einstein a introduit pour expliquer l'effet photo-électrique.

Electrodynamique quantique

La théorie quantique décrivant l'interaction entre les photons et les électrons est appelée l'électrodynamique quantique ( QED pour Quantum ElectroDynamics). Cette théorie s'est révélée très fructueuse en termes de prédiction et de précision ( 10^-11).

Il se trouve qu'on peut déduire l'électromagnétisme classique et la QED de symétries dites de "jauge" , introduites dans la théorie des électrons libres. La QED est l'exemple type d'une théorie de jauge.

Exemple des pions

Regardons comment ça marche sur un exemple simple, qui nous permettra également d'introduire le concept de champ, fonction de l'espace temps dont la quantification des excitations élémentaires seront interprétées comme des particules.

Nous nous en tiendrons à la Relativité restreinte ( la Relativité Générale conduisant à un formalisme complexe rarement nécessaire, sauf en cas de conditions extrêmes, à proximité d'un trou noir par exemple). Un traitement plus exhaustif du champ Relativiste est présenté en annexes B et C.

Un pion, par exemple, a un spin de 0 et peut être représenté par un champ scalaire où x représente la coordonnée d'espace temps x .Par une transformation de Lorentz x -> x' et le champ se transforme comme suit:

Théorie des champs relativistes

En théorie des champs Relativiste, il nous faut aussi décrire simultanément l'antiparticule- Ceci est nécessaire du fait que dans les réactions énergétiques des paires de pions peuvent émerger ex nihilo. Par exemple dans les collisions proton/proton, la réaction:

p + p -> p + p + + - , est possible si l'énergie cinétique de la paire de protons incidente au centre de masse est supérieure à l'énergie de masse au repos des deux pions. On pourrait introduire deux champs scalaires et pour décrire respectivement le pion et l'antipion. Il est plus élégant de considérer et comme la partie réelle et imaginaire d'un champ complexe :

Equation du mouvement

Si le champ est sans interactions, il va satisfaire l'équation Relativiste du mouvement:

où m est la masse du pion ( Cette équation s'appliquant aussi pour le champ conjugué * qui associé à peut produire deux états indépendants au lieu des deux fonctions et ). Cette équation est invariante par transformation de Lorentz car le d'Alembertien et m² sont invariants tous les deux.

L'équation (6.3) peut être dérivée de l'équation d'Euler Lagrange ( cf B.27)

Choix du Lagrangien

Si nous choisissons la densité de Lagrangien invariante par transformation de Lorentz L(x)

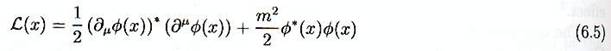
Invariance globale

On voit que (6.5) est invariant par changement de la phase d'une même valeur partout,

avec a constant, du fait de la présence des fonctions conjuguées. Ceci est appelé une invariance globale du Lagrangien.

Invariance locale

Supposons maintenant que nous voulions que le Lagrangien soit aussi invariant par un changement de phase qui pourrait avoir une valeur différente en chaque point,

Ceci est appelé une invariance locale ou encore invariance de jauge.

Tel quel , les dérivées partielles ne permettent pas l'invariance. Nous sommes amené à ajouter d'autres champs à la dérivée avec les règles suivantes:

et poser

Quand

Le champ que nous avons ainsi introduit s'appelle le potentiel électromagnétique.

Dérivée covariante de jauge

L'équation (6.6) définit _,la dérivée covariante de jauge, qui est similaire à la dérivée covariante que nous avons introduit en Relativité Générale ( cf 3.36).

L'équation du mouvement devient alors:

(6.8)

qui décrit les propriétés électromagnétiques d'un champ scalaire chargé.

Diagrammes de Feynman

La manière habituelle de description des couplages par échange de particules utilise les diagrammes de Feynman, un des contributeurs majeurs à la QED. La fig 6.2 montre un tel diagramme correspondant à l'interaction de 2 électrons par échange d'un photon.

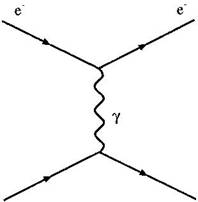
Fig 6.2 : Diagramme de Feynman représentant la diffusion de deux électrons via un échange de photon

Nous savons de l'étude de la désintégration du neutron , qu'il existe une autre interaction plus faible que l'électromagnétisme. C'est à cette "interaction faible" que les neutrinos sont sensibles, ce qui permet leur détection expérimentale. Cependant un neutrino de 1 Mev interagit si faiblement avec la matière que son trajet moyen d'interaction est d'environ 1 année lumière dans la matière, ce qui rend leur détection difficile.

6-7 Bosons de jauge massifs et mécanisme de Higgs

Interaction faible

Du fait du succès de la QED , il a paru naturel de la généraliser aux autres interactions. Dans les années 1970, une théorie de jauge de l'interaction faible a été élaborée, et sa relation avec la QED était si forte, que ces deux interactions ont été unifiées et considérées comme une seule "l'interaction électrofaible". Bien sûr à cette interaction correspond des particules échangées les bosons W± et Z⁰ . En 1982 ces particules ont été détectées au CERN à Genève. La figure 6.3 montre la désintégration b du neutron par échange d'un boson W. Nous voyons que cela se traduit par le changement de saveur d'un quark médiatisée par le courant chargé associé au boson W±.

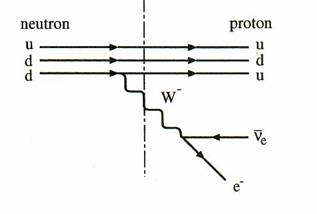
Fig 6.3 : Désintégration d'un neutron en un proton, un électron et un antineutrino

La masse de ces particules s'est révélée très élevée ( 80-90 Gev), par opposition au photon de masse supposée nulle.

Mécanisme de Higgs

Cette asymétrie de masse dans les bosons des deux interactions nécessite pour l'expliquer un mécanisme de " brisure de symétrie, appelé le Mécanisme de Higgs. Cette dernière partie de la théorie électrofaible n'a pas encore été prouvée expérimentalement. Si elle est correcte, elle implique un nouveau champ, le champ de Higgs et sa particule associée le boson de Higgs qui a la propriété de conférer une masse aux bosons W et Z ainsi que d'ailleurs aux leptons et aux quarks.

Potentiel associé au champ de Higgs

Dans le modèle standard le champ de Higgs est un champ scalaire, ce qui signifie qu'il a une densité de Lagrangien du type de celle définie par l'équation (6.5) à une différence importante près car il auto interagit , ce qui peut être décrit par un potentiel V() de la forme:

Où doit être positif pour avoir une théorie stable ( V doit être borné inférieurement).

Par contre b peut être quelconque.

S'il est positif, nous voyons que le minimum est donné par , ceci donne un état du vide unique et symétrique.

Par contre si b est négatif nous pouvons écrire:

avec

ce qui signifie que l'état de moindre potentiel, l'état du vide, qui est l'état de moindre énergie, n'est pas donné par un champ nul , mais par la valeur . La forme de l'équation du potentiel de Higgs (6.10) montrée en figure 6.4 est typique d'une brisure spontanée de symétrie et on montre que c'est la valeur supposée non nulle du vide du champ de Higgs qui confère une masse aux fermions et aux bosons W et Z.

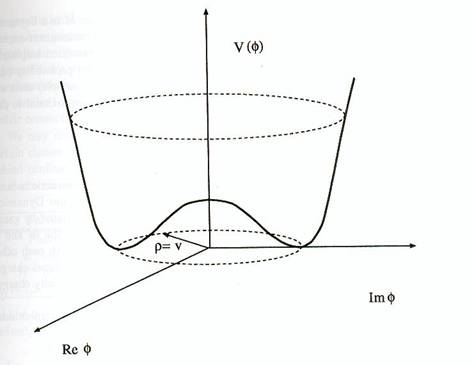
Figure 6.4 : Forme du potentiel de Higgs qui entraîne une brisure spontanée de symétrie

Lagrangien associé au champ de Higgs

Sans rentrer dans les détails de la théorie des champs, il est utile pour les applications cosmologiques de donner la forme du tenseur énergie impulsion d'un champ scalaire décrit par un Lagrangien de la forme

Le tenseur énergie impulsion associé vaut:

C'est cette expression que nous allons utiliser quand nous étudierons le modèle de l'inflation en Cosmologie.

Boson de Higgs

La particule de Higgs est sans doute la particule de la physique, la plus recherchée aujourd'hui. Les expérimentations au LEP du CERN nous indiquent que sa masse est supérieure à 90 Gev.

La masse importante des bosons de l'interaction faible expliquent la faiblesse de cette interaction, ce qui est simple à comprendre qualitativement. En examinant, dans la figure 6.3, l'état intermédiaire indiqué par la ligne verticale pointillée, on voit que cela se passe comme si le neutron s'était désintégré en un proton et un boson W. Comme l'énergie du neutron est de 0,94 Gev et celle du boson W de 80 Gev, on se demande comment c'est possible du point de vue énergétique. Avons nous commis une erreur en traçant ce diagramme? Non ,car en mécanique quantique, rappelons nous que le principe de conservation de l'énergie peut être violé pendant des temps très courts. Conformément au principe d'incertitude d'Heisenberg, nous pouvons "emprunter une énergie pendant un temps sous réserve que .

Comme une fluctuation d'énergie aussi importante est peu probable, cela explique pourquoi l'interaction faible est rare , c'est à dire faible. Une particule de masse M, dans un diagramme de Feynman, qui n'existe pas en tant que particule réelle, parce qu'elle viole le principe de conservation de l'impulsion énergie ( appelée particule virtuelle) réduit l'amplitude de transition d'un facteur 1/M² soit un facteur de 1/M⁴ pour la probabilité d'interaction ( la section efficace d'un processus de diffusion ou le rythme de désintégration selon le cas) car la mécanique quantique nous indique que cette probabilité est proportionnelle au carré de l'amplitude.

6.8 Gluons et gravitons

Interaction forte

La théorie de l'interaction forte, la QCD ( Quantum Chromo Dynamics ) peut être présentée comme l'aboutissement le plus achevé aujourd'hui de l'application de la théorie des champs quantifiés.

Gluons

La QCD nous dit que l'interaction entre les quarks est véhiculée par des bosons de jauge appelés gluons. A la différence des photons en QED ( mais conformément aux bosons de l'interaction faible) les gluons se couplent entre eux ( cf Fig 6.5).

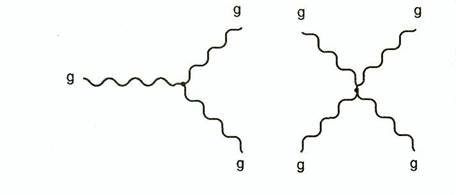
Figure 6.5 : Diagramme de Feynman montrant l'interaction de gluons

Ceci est dû au fait que les gluons sont eux mêmes porteurs de la charge de couleur de l'interaction forte. A l'inverse le photon se couple avec les particules chargées, mais est lui même électriquement neutre. En fait il y a 8 gluons différents correspondant à 8 charges différentes. La propriété de liberté asymptotique a été vérifiée en QCD, qui explique comment pendant des durées très courtes les quarks et les gluons se comportent presque comme s'ils étaient des particules libres, même si cette situation ne perdure pas sur des durées plus longues. De même, on suppose que le confinement est du à l'auto interaction des gluons, bien que cela n'a pas été prouvé rigoureusement compte tenu de la complexité analytique de la théorie. Mais il y a de fortes présomptions que ce soit le cas.

Tableau des bosons de jauge

Les particules de jauge sont synthétisées dans le tableau 6.2. En supplément on suppose l'existence du graviton, médiateur de l'interaction gravitationnelle, mais comme aucune théorie de gravitation quantique digne de ce nom n'existe aujourd'hui son existence reste hypothétique. La théorie de la Relativité Générale d'Einstein a une structure de théorie de jauge ( les transformations de jauge, étant liées à l'invariance par transformation générale de coordonnées). Le tenseur de Riemann en Relativité générale s'identifie à l'intensité du champ d'une théorie de jauge non abélienne comme la QCD, les connexions métriques jouant le rôle du potentiel de jauge.

Particule	Interaction	Masse	Charge electrique	spin
Photon	Electromagnétique	0	0	1
Boson Z⁰	Faible ( courant neutre)	91 Gev	0	1
Bosons W±	Faible ( courant chargé)	80 Gev	± 1	1
Gi, i=1,2,..,8 (gluons)	Forte	0*	0	1
Graviton (hypothétique)	Gravitationnelle	0	0	2
Boson de Higgs	Mécanisme de Higgs	> 90 Gev	0	0

* Comme les gluons sont "confinés" leur masse est indéterminée.

Signalons que des développements récents dans certaines théories de jauge, permettraient d'expliquer le mécanisme du confinement ( par des propriétés de dualité).

Etats dans le modèle standard

Si nous continuons de recenser les états d'hélicité dans le modèle standard, au 45 états déjà trouvés nous devons en ajouter deux pour le photon et pour chacun des huit gluons. Comme ils ont un spin de 1 ( s = 1) , cela signifie qu'ils peuvent avoir 2s+1 états d'hélicité, soit 3 états , mais étant sans masse seules les hélicités +1 et -1 sont permises soit deux états seulement. Les bosons W+ , W- et Z⁰ sont des particules massives de spin 1, qui possèdent donc 3 états d'hélicité chacune. Le boson de Higgs est de spin 0 et électriquement neutre, donc possède un seul état.

Le total vient donc à 90 +18 +9+1 = 118.

Expliquer l'existence de ces 118 états , est une des tâches les plus importantes de la théorie des particules moderne, dont nous pouvons espérer qu'elle nous montrera qu'il existe une structure plus vaste, unifiant ces états comme des degrés de liberté d'un objet plus fondamental

6.9 Au delà du modèle standard

Le modèle standard s’est révélé très efficace, pour expliquer et interpréter toutes les expériences et observations relatives aux trois forces fondamentales : l’électromagnétisme, l’interaction faible, et l’interaction forte. Pourtant, beaucoup de problèmes fondamentaux sont loin d’être résolus, ce qui nous incite à chercher une théorie plus fondamentale.

- Qu’est ce qui détermine les masses et les couplages des particules du modèle standard. Existe t’il un principe unificateur ?

- Nous sommes amenés à supposer que les constantes de couplage des interactions électromagnétiques, faibles et fortes dépendent du niveau d’énergie de telle sorte qu’elles s’unifient à très haute énergie (autour de 10 ¹⁵- 10 ¹⁶ GeV). Est ce une coïncidence ou existe t’il une théorie de grande unification ( TGU), qui unifie toutes les forces à cette échelle.

Pourquoi l’échelle de grande unification et l’échelle de masse de la gravitation, la masse de Planck sont elles énormément plus élevées que les masses qu’on observe dans le modèle standard ?

En particulier si on calcule la contribution à la masse du boson de Higgs, qui viendrait des corrections quantiques (particules virtuelles) à l’échelle de TGU ; les masses du boson de Higgs et aussi des bosons Z⁰ et W^+- deviennent énormes. Qu’est ce qui les empêche de devenir énorme.

- Comment décrire la gravitation quantique ? Comment unifier la gravitation quantique avec les trois autres forces fondamentales.

- Pourquoi y a t’il plus de matière que d’antimatière dans l’univers ? Dans le modèle standard, il y a une différence absolument minuscule entre les particules et antiparticules ( Ce qu’on appelle la violation CP), mais cette différence ne semble pas suffisante pour expliquer l’asymétrie baryonique de l’univers ( voir chapitre 1.3).

Ces questions demeurent sans réponse, mais nous croyons que nous avons de bonnes chances de les trouver dans les théories des supercordes et celles qui en dérivent. Dans l’attente d’une théorie achevée, nous pouvons examiner quelques caractéristiques que ces théories prédisent. En particulier la grande disparité des masses à l’échelle de la TGU et à la notre que nous avons mentionné peut s’expliquer s’il existe un nouveau type de symétrie, appelé supersymétrie dans une nouvelle théorie. Autre point intéressant, la supersymétrie semble nécessaire pour unifier la gravitation avec les autres forces.

6.9.1 Supersymétrie

La supersymétrie est une symétrie entre les bosons et les fermions. Dans une théorie supersymétrique , la première chose, c’est qu’il y ait un nombre égal d’états d’hélicité pour les bosons et les fermions. Donc, a un photon de spin 1 doit correspondre une particule de spin ½ appelée photino. Au spin ½ des fermions doivent correspondre des sfermions de spin 0 (squarks et sleptons). Les partenaires supersymétriques des Z⁰, W^+-, des gluons et des bosons de Higgs sont les zinos, les winos, les gluinos et higgsinos de spin ½. Les particules neutres sont des particules de Majorana, qui sont leurs propres antiparticules. De plus si la supersymétrie n’est pas brisée, les particules doivent avoir les mêmes masses que leurs superpartenaires respectifs. Cette dernière propriété n’est manifestement pas satisfaite ( un selectron de 511 KeV de masse est hors de question, il aurait été détecté , la limite pratique de masse obtenue par les grands accélérateurs est de 100 GeV environ !). Il est intéressant de noter que la supersymétrie peut être brisée de sorte à expliquer le problème de masse lié au boson de Higgs et cependant conserver les autres caractéristiques intéressantes de la théorie de grande unification. Pour cela, cependant, il faut que la plus légère des particules supersymétrique ait une masse inférieure à quelques centaines de GeV, ce qui suscite un intérêt évident pour des programmes de recherche de ces particules, dans les plus grands accélérateurs modernes. Beaucoup de théories supersymétriques font apparaître un nombre quantique conservé multiplicativement ( appelé parité-R) qui a la valeur +1 pour les particules ordinaires et -1 pour les particules supersymétriques. Ceci implique que les particules supersymétriques ne peuvent être créées ou annihilées que par paires. Cela implique, de fait, qu’une particule supersymétrique unique, ne peut pas se désintégrer en particule ordinaire. Si elle est lourde, elle peut se désintégrer en une particule supersymétrique plus légère plus des particules ordinaires. De ceci il résulte que la particule supersymétrique la plus légère est stable, car il n’existe pas d’état dans lequel elle puisse se désintégrer.

Si la supersymétrie existe, cela a des conséquences importantes en cosmologie. Dans l’univers primordial, la contribution des champs supersymétriques à l’énergie potentielle effective, a pu être très importante, et déclencher l’inflation, entre autres. Peu après le Big Bang , quand l’énergie thermique était élevée, comparativement à la masse des superparticules, ces particules ont pu être produites par paires en grande quantité.Puis quand l’univers s’est refroidi et étendu, la plupart se sont désintégrées sauf la plus légère qui est stable. Ces particules peuvent exister alors en tant que résidu du Big Bang. Si elles sont électriquement neutres, elles doivent interagir très faiblement avec la matière ( comme les neutrinos), mais étant massives elles peuvent contribuer à la matière noire de l’univers. Plus tard nous verrons comment calculer la densité du résidu de telles particules.

Dans les théories supersymétriques, le candidat le plus probable pour la matière noire est une superposition quantique, appelé neutralino χ de fermions neutres supersymétriques.

où est le photino , le Zino, et et sont les superpartenaires des deux particules différentes scalaires neutres de Higgs qui sont imposées par les théories supersymétriques. Les coefficients Ni sont normalisés de sorte que :

Quelquefois on définit le paramètre jaugino

et le paramètre higgsino

La masse et la composition du neutralino le plus léger, dépend de plusieurs paramètres actuellement inconnus de la théorie supersymétrique. L’approche habituelle consiste à balayer une large gamme de valeurs des paramètres, et à calculer les quantités pertinentes pour le jeu de paramètres sélectionné. Dans les modèles cosmologiques intéressants, en général, le neutralino le plus léger est un higgsino, si la masse est élevée ( de quelques centaines de GeV à quelques TeV), et un jaugino or un mélange complet de jaugino et higgsino pour des modèles prédisant des masses plus faibles ( la masse la plus faible compatible avec les expérimentations avec les accélérateurs serait de 20-30 GeV) . Aujourd’hui c’est le neutralino qui tient la corde pour la matière noire, et de nombreuses expériences tentent de le détecter. Nous y reviendrons plus tard..

6-10 Un peu de phénoménologie des particules

Dans les chapitres précédents nous avons parlé de particules variées comme les protons, neutrons, pions et leurs constituants, les quarks. Les leptons: électrons, muons et t leptons avec leurs neutrinos respectifs sont pour autant que nous le sachions élémentaires. Tous ont joué un rôle important dans l'Univers primitif quand la température était très haute, et beaucoup jouent un rôle important aujourd'hui dans divers phénomènes astrophysiques.

Bien que les quarks et les leptons sont intégrés dans le modèle standard au même plan, la phénoménologie engendrée par les quarks est bien plus riche que celle des leptons. Ceci est dû au fait que les quarks sont forcés de former des états liés, sous l'emprise de l'interaction forte.

Comme les quarks u,d et s sont bien plus légers que les trois autres, les hadrons ( baryons et mésons) qu'ils forment sont les plus faciles à étudier dans les accélérateurs, et ils ont été les premiers à être investigués expérimentalement. Avant 1973, ils étaient les seuls quarks connus.

Comme l'interaction forte (à la différence de l'électrofaible) est la même pour tous les quarks indépendamment de leur saveur, ceci doit se retrouver dans les propriétés des hadrons.

En fait le neutron et le proton sont deux particules assez semblables. Elles ont le même spin 1/2, un couplage à l'interaction forte très semblable et une masse qui ne diffère que de moins de 1%. La différence principale est la charge électrique, qui peut s'expliquer comme nous l'avons vu par la différence de charge des quarks.

En fait la petite différence de masse pourrait aussi s'expliquer par la différence des masses des quarks u et d et une possible contribution électromagnétique liée à la différence des charges.

Alors, il semble que les hadrons devraient refléter une symétrie vis à vis de l'échange des quarks u et d qui devrait produire des hadrons très similaires (en particulier la masse ne devrait pas beaucoup changer)

En mécanique quantique, les symétries telles que celle (approximative) liée à l'échange des saveurs de quarks, sont générées par ce que nous appellerons des opérateurs unitaires.

Si nous nous limitons aux quarks u et d seulement, il semble que nous pouvons remplacer le doublet (u,d) par une combinaison linéaire

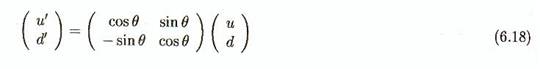
sans changer l'interaction forte. Ceci implique une symétrie appelée "invariance d'isospin" pour l'interaction forte à basse énergie. Cependant les autres quarks sont beaucoup plus massifs et en conséquence leurs symétries de saveur ne sont pas aussi bien respectées.

6.10.1 Estimation des sections efficaces

Le calcul des sections efficaces de collision et d'annihilation, et de désintégration des particules est une des tâches importantes de la physique. Nous allons ici faire une brève description de la méthode, et nous concentrer sur une estimation "à la louche" qui peut être très utile en cosmologie et astrophysique.

Pour la microphysique locale dans le modèle FLRW, nous ne considérerons que trois interactions ( électromagnétique, faible et forte). L'interaction gravitationnelle est complètement négligeable entre les particules élémentaires, par exemple la force gravitationnelle entre un proton et un électron dans un atome d'hydrogène est environ 10⁴⁰ fois plus faible que la force électromagnétique.

Par contre la gravitation, du fait de son action à grande distance doit être prise en compte pour son influence sur la métrique. Cela signifie que la dilution des densités numériques liée à la dépendance temporelle du facteur d'échelle a(t) doit être considéré. Au prochain chapitre nous verrons comment. Commençons par la force des interactions.

La force de l'interaction électromagnétique est régie par la constante de couplage électromagnétique g_em qui est simplement la charge électrique. Comme d'habitude nous prendrons la charge du proton e comme unité et nous pouvons écrire :

où Q est la charge de la particule en unités de charge du proton (pour un quark u, par exemple, Qu = +2/3). Dans notre système d'unités,

où est appelée la constante de structure qui a une valeur d'environ 1/137 à basse énergie⁴ (Habituellement on la note simplement sans l'indice.) La constante de couplage faible est d'un ordre de grandeur semblable:

avec qui est l'angle d'interaction faible ( de Weinberg) et qui a une valeur numérique donnée par . Le fait que les constantes de couplage des interactions faibles et électromagnétiques soient du même ordre de grandeur est bien sûr lié au fait qu'elles sont unifiées dans le modèle standard par l'interaction électrofaible.

(⁴ Ces constantes de couplage, comme les autres dépendent de l'échelle d'énergie, par exemple, à 100 Gev, = 1/128).

La constante de couplage de l'interaction forte g_s est passablement plus élevée. Aussi, elle décroît plus vite en fonction du niveau d'énergie que la constante électromagnétique. A des énergies de quelques Gev on a:

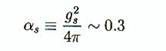(6.22)

Examinons un diagramme de Feynman pour un processus simple tel que e+e- -> µ+µ- (Fig. (6.6). L'amplitude sera proportionnelle aux constantes de couplage aux deux sommets qui dans ce cas sont toutes les deux égales à e. La section efficace étant proportionnelle au carré de l'amplitude, est alors proportionnelle à e⁴ proportionnel à (/4p)²

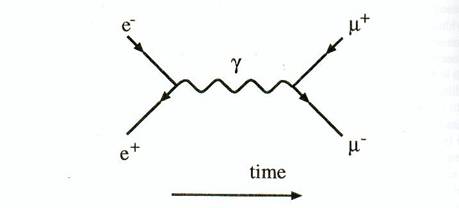
Figure 6.6: Un diagramme de Feynman représentant la transmutation d'un électron et d'un positron en une paire de Muons ( via un photon virtuel).

Si nous considérons l'énergie totale de la paire e+e- dans le référentiel associé au centre d'impulsion, nous avons vus qu'on pouvait l'exprimer E(e+) + E(e-) = . . Comme dans ce référentiel l'Impulsion totale est nulle, la quadri impulsion p= (, 0, 0,0) est identique à celle d'une particule massive de masse au repos.

La conservation de l'énergie et de l'impulsion implique que le photon dans l'état intermédiaire doit avoir cette impulsion. Comme un photon se propageant librement est sans masse, cela veut dire que ce photon est virtuel dans une large mesure. Dans la théorie quantique des champs, on montre que l'apparition d'un état intermédiaire de masse virtuelle pour une particule de masse réelle Mi provoque une réduction de l'amplitude ( de la transition) par un facteur de (appelé facteur de propagation)

(6.23)

Dans ce cas ( m_i = 0) ce qui implique un facteur de correction de 1/s.

Les particules sortantes ( ici les muons ) offrent un grand nombre de possibilités pour l'état final ( par exemple tous les angles de diffusion possibles dans le référentiel du centre d'impulsion). Ceci doit être imputé via le facteur spatial de phase , qui généralement croît avec s pour les hautes énergies. Pour une section efficace

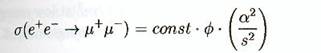
Si s est grand comparé à , et

Ce n'est pas une expression exacte. Un calcul rigoureux (voir § suivant et annexe D.2) donne 4pa²/3s, mais c'est étonnement précis et souvent assez précis pour les estimations dont nous avons besoin dans la cosmologie du big bang.

Comme la valeur de la constante de couplage faible est du même ordre que celle de l'électromagnétisme, la même formule est valide, par exemple qui s'opère via l'échange d'un W ( voir fig 6.7). La seule substitution à faire est pour le propagateur, alors:

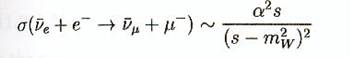
quand , cela donne, ce qui est une section efficace minuscule, pour par exemple des énergies de l'ordre du Mev ( mais remarquons l'accroissement avec l'énergie lié au facteur s ). C'est la raison historique de la dénomination "interaction faible", qui n'est pas appropriée comme nous le verrons aux hautes énergies (bien plus hautes que m_w), ou deux types de section efficace deviennent de taille semblables.

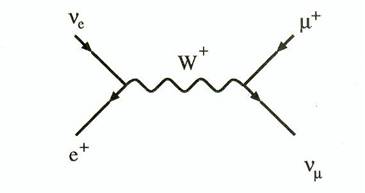
Figure 6.7 : Diagramme de Feynman représentant l'annihilation / création d'un positron et d'un neutrino électronique en un muon et un neutrino muonique.

Remarquons qu'une fois qu'on a noté les facteurs des constantes de couplage et les propagateurs, la taille de la section efficace peut souvent être estimée simplement par analyse dimensionnelle. Une section efficace à la dimension d'une surface, ce qui dans nos unités correspond à (masse)^-2. Il est très utile de vérifier que les expressions (6.25) et (6.26) ont bien les bonnes dimensions.

Un fermion a un propagateur qui se comporte en 1/m au lieu de 1/m² aux basses énergies. Ceci signifie que la section efficace de Thompson

à basse énergie peut être estimée à ( voir fig 6.8):

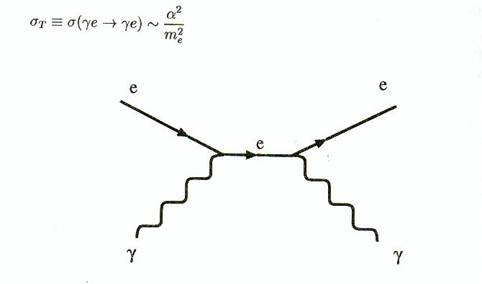
Fig 6.8 : Diagramme de Feynman représentant un processus (Diffusion Thompson)

6-11 Exemple de calcul de section efficace

Pour les applications cosmologiques et astrophysiques, les estimations suivantes simples seront satisfaisantes. Cependant il y a des cas où il sera nécessaire de faire appel à des formules plus précises ( ou quand il y aura ambiguïté sur l'échelle de masse à considérer for ces estimations). Ici nous allons proposer des estimations pertinentes dans le cadre d'applications décrites dans cet ouvrage. Les calculs détaillés nécessitent de connaître l'équation de Dirac et sont discutées dans l'annexe D. Nous résumons ici le cadre général et les principaux résultats.

6-11-1 Définition de la section efficace.

Dans l'annexe D, nous montrons que la différentielle de la section efficace pour un processus de diffusion 2 -> 2, a+b -> c+d, est donnée par l'expression.

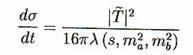
où ( cf § 2.4.3), et Ici est l'amplitude polarisée sommée de transition de la mécanique quantique élevée au carré. Les limites d'intégration pour la variable t sont données en (2.59).

Un calcul typique (annexe D) implique le calcul de l'élément de matrice en termes de s et t et d'opérer l'intégration sur t pour obtenir la section efficace globale.

Dans l'approximation d'échange d'un photon, la section efficace pour la transition:

vaut :

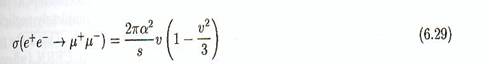
Où la seule approximation a été de négliger m_e ( ceci est justifié du fait que 1.

Ici v est la vitesse d'un des muons sortants dans le référentiel du centre d'impulsion,

Dans la limite relativiste où ceci devient :

comme indiqué précédemment.

6-11-2 Interaction de neutrinos

Pour le processus , la section efficace vaut:

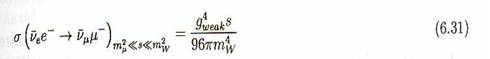
Avant que l'on sache que les bosons existent, Fermi avait écrit une théorie phénoménologique pour l'interaction faible avec une constante dimensionnée ( la constante de Fermi) G_F. La relation est :

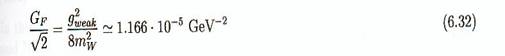
En utilisant la section efficace on peut simplement l'écrire:

Nous observons que la section efficace s'accroît avec et donc linéairement avec l'énergie du neutrino.

Quand s commence à s'approcher de m_w, le propagateur W doit être traité avec précaution. Cela peut être amélioré en l'écrivant dans la forme de Breit Wigner.

où est la largeur totale de désintégration ( environ 2 Gev) du W. Nous voyons donc qu'une amélioration significative de la section efficace est possible pour Ceci est un exemple d'effet de résonance dans le canal s. Pour un électron cible au repos cette résonance se produit se produit à 6,3 PeV (appelée résonance de Glashow). S'il existe des sources astrophysiques qui produisent des antineutrinos électroniques de telles énergies, alors les possibilités de les détecter s'en trouveraient grandement améliorées. Juste au dessus de la résonance la section efficace va re-décroître en 1/s, comme c'était le cas dans le processus

Nous pouvons remarquer que ce dernier processus , reçoit aussi une contribution d'un boson intermédiaire Z. A basse énergie elle est complètement négligeable, mais du fait de l'amplification par la résonance elle va dominer vers s = m²_z. L'étude des bosons Z au LEP du CERN utilisent cette propriété ( où toutes les autres paires fermions / antifermions sont produites sauf tt, qui n'est cinématiquement pas possible. Un calcul complet doit additionner de façon cohérente les deux contributions qui peuvent interférer de manière intéressante, produisant par exemple une asymétrie avant/arrière entre les deux muons sortants.

6-11-3 le système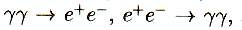

En permutant de différentes façons, les particules incidentes et sortantes, l’interaction de base (montrée sur la figure 6.8) peut décrire et .

Pour le résultat est

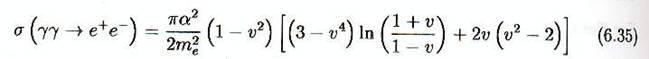
où v est maintenant la vitesse d’un des électrons produits dans le centre du moment d’inertie (impulsion) . Près du seuil, pour v petit, l’expression entre crochets peut être développée en série et donner et donc

Pour l’autre extrême, v à 1 on obtient :

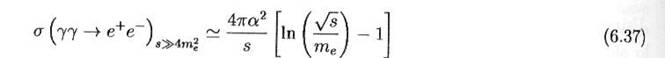
On voit avec satisfaction que nous aurions pu estimer la plupart de ces résultats, avec une bonne approximation par des arguments dimensionnels et application des règles de comptage des vertex. A basse énergie la seule échelle de masse disponible est m_e, donc on pouvait s’attendre au facteur . On pouvait s’attendre au facteur v avec un peu plus de connaissance des amplitudes d’onde partielles. A basse énergie l’amplitude l = 0 (onde S) doit dominer, et ceci contribue à la section efficace proportionnellement à v. Une onde partielle l contribue à la section efficace totale avec un terme proportionnel à v ^{2l +1}. [Nous voyons ( 6.29) que dans le cas l’onde S domine à basse énergie, mais que quand v 1, la contribution de l’onde P est 1/3]

A haute énergie, quand m_e peut être négligé, la dimension est portée par s. Seul le facteur de correction logarithmique dans ( 6.37) ne pouvait pas être facilement deviné.

Il ressort de ces formules que la section efficace de croît depuis un seuil jusqu’à un maximum à des énergies intermédiaires et décroît environ en 1/S à plus haute énergie ( voir fig 6.9).

Les résultats de la réaction inverse sont bien sûr très similaires. Maintenant le processus est toujours au dessus du seuil. Pour v à 0 ( avec v qui est maintenant la vitesse d’une particule incidente dans le centre d’impulsion, est toujours donné par la formule , le facteur de flux en dans ( D7) diverge. Comme les photons sortants vont toujours à la vitesse v = c = 1, il n’y a pas de facteur de suppression d’onde partielle, et on peut s’attendre à ce que la section efficace à basse énergie se comporte comme :

et le comportement à haute énergie obéit à la même formule avec m_e² remplacé par s ( et un éventuel facteur logarithmique). Ces suppositions sont portées par le calcul effectif qui donne :

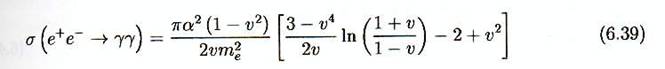
Notons la similitude avec (6.35)

Finalement intéressons nous à la diffusion Compton D’habitude on a un faisceau de photons d’énergie « oméga » qui frappent des électrons au repos. Pour un angle de diffusion « theta », par rapport au faisceau incident, l’énergie du photon sortant « oméga’ » est donnée par la conservation de l’énergie impulsion selon :

Dans ce référentiel, la section efficace différentielle non polarisée, calculée en premier par Klein et Nishina vaut

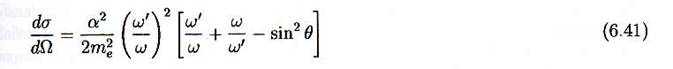
En intégrant sur tous les angles possibles de diffusion, cela donne la section efficace totale

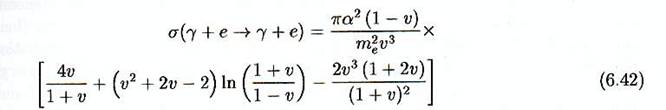
où v est maintenant la vitesse incidente de l’électron par rapport au centre d’impulsion Si on développe ce résultat autour de v = 0, on retrouve le résultat de la diffusion Thompson.

et pour s grand ( régime de Klein Nishima) on a

Nous voyons que pour des énergies bien supérieures à me, c’est à dire en régime Klein Nishina, la section efficace de diffusion Compton décroît rapidement.

Cette formule a beaucoup d’applications. Dans le cas classique de diffusion Compton, l’énergie du photon sortant est toujours inférieure à celle du photon entrant. Donc des photons énergétiques traversant un « gaz » d’électrons froids vont être refroidis par la diffusion Compton. Dans d’autres cas ( par exemple, le RFC traversant un amas de galaxies avec gaz chaud) , les électrons énergétiques peuvent transférer de l’énergie aux photons et les « réchauffer », ce qu’on appelle parfois l’effet Compton inverse ( bien que, si nous exprimons l’énergie en fonction de s , ce soit la même formule qui s’applique dans les deux cas).

Dans le cas d’une application numérique concrète, pour la section efficace (qui a les dimensions d’une surface), dans nos unités, un facteur de conversion utile est

La figure 6.9 résume ces résultats numériques. Les sections efficaces sont montrées (en cm²) pour et en fonction de l’énergie disponible au centre d’impulsion, en unités de masses d’électron

où pour et et pour la diffusion Compton Nous voyons sur cette figure les différents comportements à basse énergie ( y petit) déjà présentés, mais elle montre une décroissance similaire à haute énergie.

Un autre processus d’un grand intérêt en astrophysique st le rayonnement de freinage. Il s’agit démission de photons par des particules chargées qui sont accélérées ou décélérées. Si cette accélération est due à un mouvement circulaire dans un champ magnétique, on parle de rayonnement synchrotron. Dans ces processus, à la différence de la diffusion Compton, le nombre de photons peut changer. Ceci est nécessaire si l’équilibre thermique doit être maintenu, car nous avons vu que la densité numérique de photons dépend fortement de la température. La plupart des photons produits, par ce rayonnement de freinage, ont des énergies faibles (grande longueur d’onde).

Si des électrons rapides passent par là, ces photons poussifs peuvent être revigorés par une diffusion Compton inverse. Ceci peut explique les observations de photons très énergétiques dans les noyaux de galaxies actives ( voir chapitre 14).

Pour plus de détails référez vous à un ouvrage traitant de l’électrodynamique quantique dans la théorie quantique des champs.

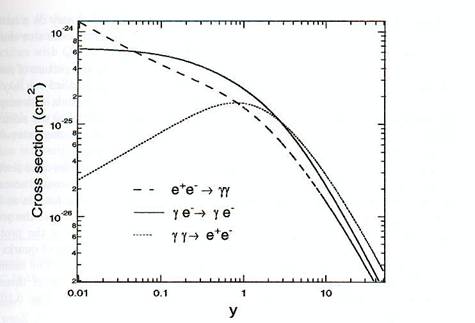
Figure 6.9 : Section efficace (en cm²) pour les processus d’annihilation de photons, et la diffusion Compton en fonction de l’énergie (en masses d’électrons) disponible au centre d’impulsion

6-12 Processus impliquant les Hadrons

En fait les calculs développés ci avant s'appliquent mal du fait que la constante de couplage liée à l'interaction forte est élevé ( 0,2 à 10 Gev) et que l'approximation au premier ordre qui était permise dans le cas précédent ( constante de couplage << 1 ) ne donne plus de résultats corrects.