ANNEXE B
Dynamique Relativiste
B1. Mécanique classique
Formulation Lagrangienne.
L'équation
du mouvement d'Euler Lagrange s'obtient en exprimant que l'intégrale d'action
du Lagrangien entre deux points est extremum sur la trajectoire.
dòL (qi, q'i,t) dt = 0 (B4)
On en déduit
les équations du mouvement
¶L/¶qi - (d/dt)(¶L/¶q'i)
= 0 (
B8)
Que l'on
peut exprimer sous sa forme la plus générale si le Lagrangien dépend d'un champ
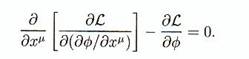
Définition du Hamiltonnien
H = Si pi.q'i
- L [ q, q'(p,q)] (B12)
Avec les
moments conjugués
pi
= ¶L (q,q')/¶q'i (B11)
L'équation
du mouvement sous sa forme Hamiltonnienne est alors
q'i
= ¶H/¶pi , p'i = ¶H/¶qi
(B15)
avec
q'i = ¶H/¶pi
, - ¶L/¶qi
= ¶H/¶qi (B16)
Prenons un
exemple simple:
![]() (B.17)
(B.17)
Cela donne
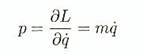 (B-18)
(B-18)
Comme q' =
p/m. Alors
![]() (B.19)
(B.19)
Les
équations de Euler Lagrange
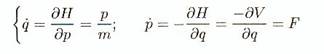 (B.20)
(B.20)
donnent alors mq" = F, comme on s'y
attend.
B.2 Champs Classiques
B2-1 Etablissement de l'équation de Klein Gordon
Considérons
un exemple important de notre formalisme. Considérons un système de N
particules, se déplaçant sur une dimension, connectées entre elles par des
ressorts de masse supposée nulle générant une force de rappel constante k (voir Fig. B.2). Les particules sont séparées les unes
des autres par une distance"a" à l'équilibre. Soit fi l'écart
par rapport à la position d'équilibre de la
particule i. Alors le Lagrangien est
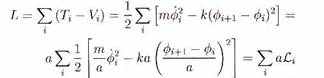 (B.21)
(B.21)
Où Li
est la contribution à la densité de
Lagrangien (Lagrangien par unité de longueur) de la particule i. Nous
pouvons passer à la limite,
i ® x, Si®ò dx, fi ®f(x), (fi+l - fi)/a ®¶f/¶x, m/a ®r (densité de masse) et
ka ®k , ( module deYoung). Le
Lagrangien continu devient alors
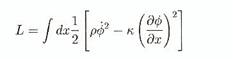 (B.22)
(B.22)
Nous pouvons
alors écrire l'action
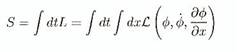 (B.23)
(B.23)
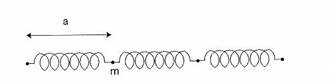
Figure B.2:
système de particules classiques identiques de masse m, connectés par des
ressorts de force constante k. La distance à l'équilibre entre les particules
est a.
Avec la
densité de Lagrangien
(B.24)
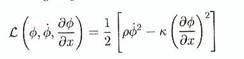
Dans cet
exemple, f(x, t) est le champ de déplacement.
Un champ est une fonction de l'espace et du temps: Il contient un nombre
infini de degrés de libertés. (Pour spécifier complètement un champ, il faut
donner sa valeur en tout point de l'espace et du temps). La construction que
nous avons fait dans cet exemple unidimensionnel est
facile à généraliser à trois dimensions. Alors
![]() (B.25)
(B.25)
Ce qui nous permet d'écrire les équations d' Euler Lagrange.
![]() (B.26)
(B.26)
Nous
remarquons que nous pouvons écrire (B.26) sous sa forme relativiste invariante.
![]() (B.27)
(B.27)
Ceci est
invariant par transformation de Lorentz, si L étant une densité de
scalaire (on a, L'(x' m) = L(xm) en RR
Comme
premier exemple réaliste nous considérons un champ scalaire réel j(x) (Ceci
peut être par exemple le champ scalaire de Higgs de
la physique des particules). La densité de Lagrangien non triviale, la plus
simple est donnée par
(B.28)
![]()
L'équation
d' Euler Lagrange (B.27) donne l'équation du mouvement.
![]() (B.29)
(B.29)
soit
L'équation de Klein Gordon.
![]() (B.30)
(B.30)
qui est une équation d'onde relativiste comme nous l'avons déjà
remarqué.
[ remarquons qu'on peut directement dériver
cette équation de l'expression de l'énergie en Relativité Restreinte
E² = p²c² +
m²c4
En associant
l'opérateur ih¶t pour l'énergie et (h/i)
¶xi pour le
moment cinétique et en l'appliquant à la
fonction d'onde.]
Il y a aussi
une formulation Hamiltonnienne de la théorie
classique des champs. Aux coordonnées généralisées j(r, t) au point
(t, r) de l'espace temps, il y a un moment canonique p(r,t), défini par
![]() (B.31)
(B.31)
Pour le
champ scalaire réel à potentiel indépendant du temps, cela donne
![]() (B.32)
(B.32)
La densité
de Hamiltonnien est alors
![]() (B.33)
(B.33)
En intégrant
cette densité sur l'espace, nous obtenons le Hamiltonnien
complet, H = òv d3rH qui
représente l'énergie totale du champ.
B2-2 Quelques rappels généraux sur l'espace de Hilbert et son utilisation en Mécanique quantique
L'espace de Hilbert
États et vecteurs, observables et opérateurs
Le
remaniement conceptuel impliqué par le quantum d'action, amorcé par la
modification du statut des concepts, poursuivi par l'élaboration du concept d'amplitude
de probabilité, atteint sa forme achevée, épanouie, avec l'espace de Hilbert. Rarement
autant qu'à l'occasion de ce remaniement l'harmonie a été aussi bonne entre les
besoins du développement de la physique théorique et les moyens que fournissent
les mathématiques. L'espace de Hilbert
est, au départ, une pure construction mathématique, mais qui se trouve répondre
parfaitement à ce qui était nécessaire à l'élaboration de la théorie quantique. Si l'espace de Hilbert n'avait pas été
découvert, il aurait fallu l'inventer pour les besoins de la théorie quantique
!
Mathématiquement,
l'espace de Hilbert représente une généralisation du concept d'espace vectoriel métrique (l'espace
ordinaire et l'espace-temps de Minkowski sont des espaces vectoriels métriques).
L'espace de Hilbert est un espace vectoriel de
fonctions.
Dans notre cas ces
fonctions vont être les fonctions d'onde y que l'on considère comme un
vecteur, dont une base est fournie par un ensemble ( infini) de fonctions yi orthogonales et
normées au sens où l'intégrale du
produit satisfait à òyiyj = dij
Les
transformations qui agissent sur des vecteurs de l'espace et les transforment
en d'autres vecteurs du même espace sont des opérateurs*. Vecteurs et opérateurs ont des propriétés de
linéarité : toute combinaison linéaire, à coefficients complexes, de vecteurs
est un vecteur ; un opérateur transforme un vecteur en un autre vecteur, et
toute combinaison linéaire de vecteurs en un vecteur. Le produit scalaire de deux vecteurs associe
à ces deux vecteurs un nombre complexe qui dépend linéairement de chacun des
deux vecteurs. Ce produit scalaire
généralise les produits scalaires que nous avons rencontrés dans l'espace
ordinaire et l'espace-temps de Minkowski.
Dans l'espace de Hilbert, le produit scalaire se définit à l'aide de
l'intégrale du produit des deux fonctions qui représentent les deux vecteurs.
Comme les
concepts quantiques sont adaptés à la description des phénomènes, le formalisme
de la théorie quantique s'intéresse d'une part aux états du système physique et d'autre part aux grandeurs physiques observables relativement à ce
système. Les états sont associés aux
vecteurs d'un espace de Hilbert, et les observables aux opérateurs qui agissent
dans cet espace. Cette double
association répond à tous les problèmes que nous avons évoqués plus haut : les
amplitudes d'état sont les vecteurs de l'espace de Hilbert, la linéarité de
l'espace de Hilbert assure l'additivité des amplitudes d'état ; l'amplitude de
transition entre deux états est associée au produit scalaire des deux vecteurs
qui les représentent ; l'association d'un opérateur à une observable permet de
prendre en compte l'effet sur le système de l'acte de mesure :
Mesure d'observable
Mesurer une
observable relativement à un système dans un état donné modifie, en général,
l'état du système de la même façon qu'un opérateur transforme un vecteur en un
autre vecteur.
C'est
pourquoi tout état du système ne permet pas nécessairement la mesure de toute
observable. Mais une notion essentielle
des espaces de Hilbert nous permet de définir les états permettant la mesure
des observables. Un vecteur de
l'espace de Hilbert est dit vecteur propre* d'un opérateur si l'action de cet
opérateur sur ce vecteur consiste à le multiplier par un nombre appelé valeur
propre.
Vecteurs
propres et valeurs propres sont très utiles si on veut associer vecteurs et
états, opérateurs et observables : puisque, à une constante multiplicative
près, un vecteur propre est laissé invariant par l'action de l'opérateur,
l'état physique associé à ce vecteur permet la mesure de l'observable associée
à l'opérateur dont le vecteur est vecteur propre. Quant à la valeur propre, on pourra
l'associer à la valeur de l'observable mesurée dans l'état. Comme la valeur d'une grandeur physique
mesurable est un nombre réel, les opérateurs associés aux observables doivent
avoir des valeurs propres réelles ; les opérateurs qui ont cette propriété sont
dits hermitiques*.
Opérateurs Hermitiques
[Rappelons
qu'un opérateur Hermitique est égal à
son adjoint ( A = A+), l'opérateur adjoint étant le
transposé du conjugué ( f et g étant des fonctions) .
òf.A+.g .dt = òg.A*.f .dt , A* étant
l'opérateur complexe conjugué de A.
Si A est Hermitique, cela
implique entre autre que òg*.(Ag) dt = [òg*(Ag) dt ]*
Si A est Hermitique et linéaire ,
l'intégrale òg*.(Ag)
dt est alors
réelle.
Ce qui est
nécessaire car cette équation représente des grandeurs physiques réelles
Par exemple
l'opérateur A = ¶²/¶x est Hermitique, ¶/¶x ne l'est pas
mais i¶/¶x l'est.
Fait
important en mécanique quantique, le Hamiltonien est
un opérateur Hermitique.
Pour
terminer sur ce point signalons que si A et B sont des
opérateurs Hermitiques, leurs produits AB et BA en général
ne le sont pas mais que (AB + BA)/2 l'est. Le produit n'est pas
nécessairement commutatif. Si AB = BA, les opérateurs commutent,
mais si AB ¹ BA les opérateurs ne
commutent pas.]
Opérateur Hamiltonien
L'opérateur
le plus important de la théorie quantique est l'opérateur hermitique
associé à l'énergie totale du système, le hamiltonien*. L'ensemble des valeurs propres du hamiltonien est appelé spectre du système. Pour un système atomique, le spectre comporte
une suite discrète de valeurs propres, correspondant aux niveaux d'énergie de
l'atome (niveau fondamental et niveaux excités), et un continuum correspondant
à l'ionisation par arrachement d'électron.
Complémentarité et relations de commutation
En théorie
classique, les observables (les quantités physiques à mesurer) ne sont pas
associées à des opérateurs mais à de simples nombres. Le produit de deux nombres est commutatif:
ab=ba
par contre, le produit de deux opérateurs n'est pas
nécessairement commutatif. On dit que
deux opérateurs A et B commutent si leur commutateur* noté [A,B]=AB-BA est nul.
Si deux
opérateurs commutent, les vecteurs propres de l'un sont vecteurs propres de
l'autre. Puisque des opérateurs qui
commutent partagent leurs vecteurs propres, on peut dire que les observables
qu'ils représentent sont compatibles : on peut mesurer ces observables dans le
même état.
En revanche., on voit clairement qu'une caractéristique de
l'incompatibilité entre des observables est la non-commutation
des opérateurs qui les représentent.
Supposons
que deux observables soient quantiquement
incompatibles, comme par exemple la position et l'impulsion d'une particule que
nous notons q et p, les opérateurs qui les représentent Q et P ne commutent
pas. Un vecteur propre de Q par exemple
représente un état dans lequel la position peut être mesurée. Mais ce vecteur propre n'est pas vecteur
propre de P. L'action de P sur ce vecteur le transforme en un vecteur qui n'a
rien de commun avec lui. Cela signifie
qu'on ne peut pas mesurer l'impulsion dans un état où la position peut être
mesurée, et vice versa. C'est
l'expression rigoureuse de l'inégalité de Heisenberg que nous avons mentionnée
au chapitre précédent.
La
commutation (et surtout la non-commutation) des
observables est l'une des propriétés les plus spécifiques de la théorie quantique. C'est elle qui permet de donner un sens
précis à l'idée de la complémentarité.
Une
représentation est définie par un ensemble* complet d'observables qui
commutent. Les vecteurs propres communs
à toutes ces observables définissent une base* de l'espace de Hilbert. Si l'ensemble d'observables qui commutent est
bien complet, la base de l'espace de Hilbert est aussi complète. Cela signifie que tout vecteur de l'espace de
Hilbert, c'est-à-dire l'amplitude d'état de tout état possible du système, peut
être obtenu par combinaison linéaire des vecteurs de base. Autrement dit, une représentation est
déterminée par un ensemble complet d'observables compatibles,
fournissant toute l'information qu'il est possible de recueillir sur un système
quantique.
Ce qui est
nouveau par rapport à la théorie classique, c'est qu'il peut exister une
deuxième représentation, c'est-à-dire un deuxième ensemble complet
d'observables qui commutent, mais qui ne commutent pas avec celles de la
première représentation. On dit alors
que les deux représentations sont complémentaires.
L'espace de
Hilbert et la complémentarité représentent une généralisation de la conception
de l'espace, de la conception de la covariance et de la conception de
l'objectivité face aux contradictions de l'élémentarité. Si on considère l'espace comme un espace d'objectivité, permettant d'appréhender les propriétés
intrinsèques, indépendantes de la réalité, l'existence du
quantum d'action rend insuffisant l'espace ordinaire de la physique
classique pour penser la nouvelle objectivité quantique. C'est l'espace de Hilbert qui est l'espace de
l'objectivité quantique. Quant à la
complémentarité, elle généralise, dans cet espace, le concept de covariance qui
fonctionnait dans l'espace ordinaire, les ensembles complets d'observables qui
commutent jouant le rôle de référentiels.
B.3 Champs quantiques Relativistes
Une
application importante de la théorie des champs scalaires est dans la physique
du solide. Il ressort clairement ( c'est le cas de le
dire) de la dérivation de la théorie classique des champs scalaires
classiques décrite au § B.2, que ceci
décrit les vibrations d'un cristal, qui sont des ondes acoustiques. Si nous
remplaçons la vitesse de la lumière par la vitesse du son, nous pouvons
utiliser la théorie quantique des champs scalaires que nous allons développer
ci après pour décrire les vibrations quantifiées appelées phonons.
B.3.1 Le Champ de Klein Gordon
Quand nous
quantifions une particule ponctuelle en mécanique quantique, nous traitons les
coordonnées généralisées q (les coordonnées cartésiennes xi dans le cas le plus
simple ) et les moment cinétiques pi comme des
opérateurs. Ils satisfont les relations
de commutation de la mécanique quantique.
![]() (B.34)
(B.34)
Et la
fonction d'onde y est la
représentation du vecteur d'état sur lequel, ces opérateurs agissent.
L'équation
de Klein Gordon étant une équation d'onde, elle doit avoir des solutions de
type ondes planes. Nous pouvons imaginer
notre système inclus dans une grande boîte de volume V, et nous imposons des
conditions aux limites de la boîte habituelles telles que cela corresponde à un
nombre entier de périodes ( nous ferons éventuellement tendre la limite V ®¥, bien sur).
Développons le champ scalaire réel j à un instant donné en termes
d'ondes planes.
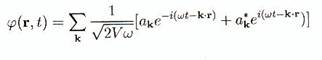 (B.35)
(B.35)
Où nous avons introduit 1/Ö(2Vw) pour normaliser
correctement, et où l'insertion dans l'équation de Klein Gordon montre que w = w(k) = Ö(m²+k²) qui décrit
l'énergie d'une particule relativiste de masse µ et d'impulsion k.
Nous pouvons
alors écrire les facteurs dans les exponentielles kx = kµxµ avec k0 =w.
Comme le
champ de K-G est écrit sous forme de
somme de composantes indépendantes qui satisfont une équation d'onde, qui ont
un mouvement harmonique, il est naturel de quantifier chaque mode de la même
manière que nous le faisons habituellement pour un oscillateur harmonique. En
insérant (B.35) dans (B.33) pour la densité de Hamiltonnien
et en réalisant l'intégration sur tout le volume V, nous obtenons:
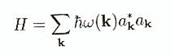 (B-36)
(B-36)
où nous avons temporairement réintroduit un facteur h pour
montrer la similitude avec l'expression de l'énergie d'un oscillateur
harmonique quantique. En fait si nous interprétons ak et a*k ® a+k comme le
fait d'élever ou d'abaisser des opérateurs, remplissant les relations de
commutation.
![]() (B.37)
(B.37)
alors j et p vont
satisfaire les relations de commutation (B.34). Si on recalcule le Hamiltonien en utilisant (B.37) on trouve
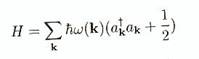 (B.38)
(B.38)
[ voir à cet effet la démonstration de l'énergie d'un oscillateur
harmonique linéaire à une dimension, par la méthode polynomiale (Sommerfeld): A
partir du Hamiltonnien correspondant à l'oscillateur
harmonique, on commence par chercher les solutions asymptotiques à l'infini
(ondes planes), puis on cherche une fonction d'onde y (x) égale au
produit de la solution asymptotique par une fonction f(x). On
développe f(x) en puissances de
x et avec un peu de calcul on obtient une relation de récurrence entre les coefficients. Pour que cela reste
borné, on est amené à imposer des contraintes ( l= 2n +1) sur un des
paramètres du problème l= e / a
avec e = 2mE/h² et a² = (mw0 /h)² , ce qui
impose E =( n +1/2 )hn0 , où on voit apparaître une énergie minimum
pour n =0. De cela on peut calculer la fonction d'onde complète ( polynômes d'Hermite …)…cf cours
" notions de mécanique quantique INSA 4° année")]
D'habitude,
on ignore la contribution constante issue de la somme des modes zéro (les
termes en hw/2). Il y a des cas où par contre, on devra en
tenir compte comme nous le verrons plus loin.
Maintenant
nous pouvons utiliser toute la machinerie que nous avons apprise en étudiant
l'oscillateur harmonique dans le contexte le la mécanique quantique non
relativiste. Nous définissons l'état de base, comme celui annihilé par tous les
ak: c'est à dire
![]() (B.39)
(B.39)
pour tout k. Un état normalisé avec nk excitations dans
le mode k est donné par
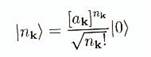 (B40)
(B40)
Comme H est
une somme d'oscillateurs harmoniques indépendants, les valeurs propres sont les
produits directs.
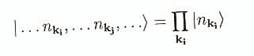 (B.41)
(B.41)
L'énorme
espace de Hilbert défini par toutes ces bases s'appelle un espace de Fock.
Compléments sur l'espace de Fock
[ La quantification du champ électromagnétique est,, bien
évidemment, un problème de la relativité quantique, puisque les photons se
meuvent à la vitesse de la lumière.
L'idée essentielle est de traiter comme un opérateur quantique le quadrivecteur potentiel du champ électromagnétique. La complémentarité s'applique au champ
électromagnétique quantifié : la description en termes de particules (photons)
correspond à la représentation en
impulsions, la description ondulatoire (donnée du champ électrique et du
champ magnétique en tout point d'espace-temps) correspond à la représentation en positions.
La
principale nouveauté par rapport au cas non relativiste (que l'on appelle la
première quantification) tient au fait qu'on ne peut plus se contenter de
l'espace de Hilbert des états à une particule ou à un nombre fini de
particules. Pour décrire les états d'un
champ électromagnétique, dans la représentation en impulsions, on a recours à
un espace plus vaste que l'espace de Hilbert, l'espace de Fock,
qui est une superposition infinie d'espaces de Hilbert, comprenant d'abord le
vide, espace à zéro photon, puis l'espace à un photon, puis l'espace à deux
photons, etc.
Dans cet
espace de Fock, le champ électromagnétique est
représenté par des opérateurs dits de création* et d'annihilation* de photon :
l'opérateur ak+ crée un photon d'impulsion k, et
l'opérateur ak annihile un photon d'impulsion k.
L'opérateur de création fait passer de l'espace de Hilbert à n photons à celui
à n + 1 photons ; et l'opérateur d'annihilation fait, à l'inverse, passer de
l'espace de Hilbert à n photons à celui à n - 1 photons (sur le vide, l'action
d'un opérateur d'annihilation donne zéro).
On peut définir un opérateur
nombre de photons. Tout état à n
photons est représenté par un vecteur propre de l'opérateur nombre de photons
avec la valeur propre n.
La dualité onde-corpuscule, étendue par de Broglie aux ondes de
matière, conduit aussi au concept proprement quantique de champ de matière. Un champ
quantique de matière est un ensemble d'opérateurs, de création et d'annihilation
de fermions. Le concept d'espace de Fock peut être étendu aux fermions et aussi aux systèmes
mixtes, comportant des fermions et des bosons.
En fait, le
formalisme de l'espace de Fock que nous avons
introduit à propos de la relativité quantique s'est révélé d'une très grande
utilité pour décrire les systèmes quantiques statistiques (à grand nombre de
particules), même en dehors des effets relativistes. (C'est d'ailleurs la
raison pour laquelle on parle, à propos des particules indiscernables, des statistiques de Bose-Einstein
et de Fermi-Dirac.) L'espace de Fock
permet en effet de décrire statistiquement un système quantique à grand nombre
de particules en l'absence d'interaction.
En théorie statistique, il est très important qu'en l'absence d'interaction
il n'y ait pas de corrélations. Or, les
effets quantiques induisent des corrélations même en l'absence d'interaction -
les propriétés de symétrie ou d'antisymétrie par permutation de particules
identiques impliquent l'existence de telles corrélations. Avec le formalisme de l'espace de Fock, on met l'accent, non plus sur les particules qui sont
dans tel ou tel état, mais sur les états qui sont occupés ou pas par des
particules. L'espace de Fock est un ensemble multiplement infini d'états, chaque
état étant caractérisé par un nombre* d'occupation. Si les particules sont des bosons, le nombre
d'occupation est un entier arbitraire positif ou nul, si les particules sont
des fermions, le nombre d'occupation vaut zéro ou un (à cause du principe
d'exclusion de Pauli). Si on a un
système sans interaction, les états peuvent être remplis ou vidés des
particules qui les occupent, indépendamment les uns des autres : dans l'espace
de Fock, ainsi conçu, il n'y a pas de corrélation
quantique en l'absence d'interaction.
Alors que
l'espace de Hilbert constitue la généralisation quantique de l'espace de la
mécanique classique, on peut avancer l'idée que l'espace de Fock
est la généralisation quantique de l'espace temps de la relativité. Les dimensions spatiales sont représentées
par la complémentarité qui fonctionne dans chacun des espaces d Hilbert, tandis
que la dimension temporelle serait liée au nombre de particules. ]
Opérateurs de création et d'annihilation
Pour donner
une interprétation physique des états (B.41), nous notons
![]() (B.42)
(B.42)
où e(k) = hw(k). Alors nous pouvons interpréter (B.41) comme
un état à de multiple particules, chacune de masse m, où nk1, représente
le nombre de celles d'impulsion kl, nk2,
celles d'impulsion k2, etc. C'est pourquoi les opérateurs d'élévation et
d'abaissement, a+k et ak, sont habituellement appelés
opérateurs de création et d'annihilation: a+k agissant sur l'état du vide
crée une particule avec un vecteur d'onde k. Avec ce formalisme nous sommes
capables de traiter des processus où des particules d'impulsion donnée sont
créées ou détruites: des processus de collision par exemple.
B.3.2 Champ électromagnétique.
La méthode
utilisée pour quantifier un champ scalaire est très générale. Nous pouvons
l'utiliser, pratiquement en l'état pour quantifier le champ électromagnétique Aµ
(r, t). Nous avons vu en (2.80) comment nous pouvons décrire le champ
de potentiel quadrivectoriel classique dans la jauge
de rayonnement k.A = 0, A0 =
0. Il ne contient que deux degrés de liberté pour un
quadrivecteur impulsion donné kµ. Nous avons introduit les vecteurs de
polarisation em1,2 orthogonaux
entre eux et à la direction de propagation k.
Le développement en série de Fourier de Aµ, peut alors
être écrit
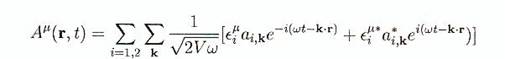 (B.43)
(B.43)
Considérons
les coefficients de Fourier comme les opérateurs d'annihilation et de création
satisfaisant:
![]() (B.44)
(B.44)
L'interprétation
physique est alors que a+ik crée un
photon de vecteur de polarisation e1m de vecteur
d'onde k. Alors l'état de Fock peut être
construit de la même manière que pour le champ scalaire.
B.3.3 Champ scalaire chargé
Il apparaît
que nous ne pouvons pas décrire des particules chargées avec un champ scalaire
réel. Pour ce faire, nous devons utiliser un champ scalaire complexe. Les
calculs sont très similaires cependant. Une densité de Lagrangien qui convient
est donnée par:
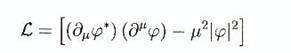 (B.45)
(B.45)
Si on traite
j et j* comme des
champs indépendants, les équations de Euler Lagrange deviennent
(B.46)
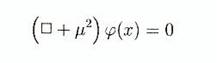
(x dénote xµ) et
![]() (B.47)
(B.47)
Le
développement en série de Fourier décrit maintenant un champ non hermitien, et
prend la forme:
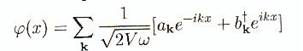 (B.48)
(B.48)
Et des
relations de commutation canoniques des champs classiques j et j* on déduit
![]() (B.49)
(B.49)
Il apparaît
alors que nous avons deux types de "particules" de même masse µ,, crées par a+
et b+, respectivement.
Quand nous couplons l'électromagnétisme à ce champ scalaire complexe, on
peut voir que les a-particules et les b-particules ont des signes opposés pour la charge
électrique. Ce formalisme inclut donc ( et en fait
prédit ) l'existence d'antiparticules.
Le couplage
à l'électromagnétisme est réalisé le plus simplement en utilisant la contrainte
de couplage minimum pµ -> pm - eAm, où
conformément à la mécanique quantique pm -> i¶m.
[ On retrouve quelque chose qui rappelle la transformation
opérée quand nous avons introduit le champ de jauge électromagnétique. Pas
étonnant puisqu'on parle du champ électromagnétique associé au couplage de particules chargées, cf document joint en annexe 1].
En Insérant ceci dans (B.45) et utilisant les
développements en termes d'opérateurs de création et d'annihilation pour j et Aµ, nous
trouvons des termes d'interaction de différents types. Quand on les intègre sur l'espace temps
certains disparaissent ( dû à la conservation de
l'énergie et de l'impulsion), mais nous obtenons, par exemple, un terme qui
peut détruire un photon, et créer un boson scalaire positif ou négatif ou vice
versa. Ces termes comportent un facteur e. Des termes en carré de Aµ vient une
contribution qui correspond à un couplage entre deux photons ou deux bosons j en un point
(un terme appelé "mouette" ou de contact). Il est proportionnel à e². Ces termes de couplage fondamentaux sont la
base pour déterminer les règles de Feynman de la théorie. Pour l'électrodynamique quantique scalaire ( QED scalaire), nous avons les diagrammes décrits par la Fig. B.3.
De plus les
propagateurs que nous avons rencontrés au § 6.10 sont donnés par les inverses
(dans l'espace de Fourier ) des formes quadratiques
des champs. Elles sont donc les fonctions de Green pour la théorie. Par exemple
l'équation de Klein Gordon :
![]() (B.50)
(B.50)
peut être inversée trivialement, car la transformée de Fourier de
la fonction d est l'unité. Alors
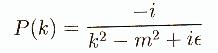 (B.51)
(B.51)
Ici, la
partie imaginaire est ajoutée pour définir comment traiter le propagateur
" dans sa couche de masse" c.a.d quand la
condition " dans la couche de masse" k² = m² est satisfaite. Il apparaît qu'ajouter une
petite partie imaginaire permet d'arriver à un état correspondant à une
particule libre d'énergie positive. Comme nous savons que le champ du photon
dans la jauge de rayonnement ( ou de Feynman) obéit à
une simple équation d'onde ƒAm = 0 (2.79), il correspond au propagateur
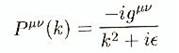 (B.52)
(B.52)
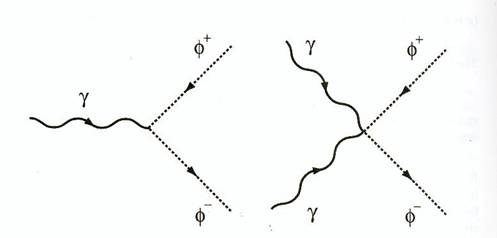
Figure B.3:
Diagramme de Feynman pour l' interaction entre photons
et un champ chargé scalaire ( QED scalaire).
Le diagramme sur la gauche est proportionnel à e, et celui sur la droite
est proportionnel à e²
.
B.4 Résumé
L'équation
d' Euler Lagrange pour un champ f s'écrit:
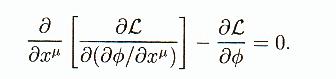
Pour un
champ scalaire la densité de Lagrangien
la plus simple invariante relativistement est:
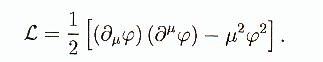
L'équation
du mouvement qui en découle est l'équation de
Klein Gordon
![]()
Une équation
d'onde relativiste pour un champ scalaire ( sans spin)
de masse µ.
La
quantification est plus simple sur un développement en série de Fourier, où
chaque mode avec un vecteur d'onde k contribue
indépendamment au Hamiltonien:
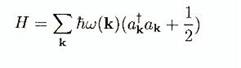
Un champ
scalaire électrique chargé est efficacement décrit par un champ complexe f avec la
densité de Lagrangien
![]()
L'interprétation
physique nécessite deux types de particules, chacune de masse µ.L'émergence de
telles antiparticules est une caractéristique générique de la théorie quantique
relativiste des champs.