D’UNE NOUVELLE ÈRE OBSERVATIONNELLE"
à l'occasion de la réunion de la Commission de Cosmologie.


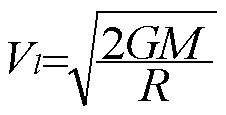 Que remarque-t-on de cette formule : la
vitesse orbitale ne dépend pas de la masse du corps en orbite, c'est
fondamental.
Que remarque-t-on de cette formule : la
vitesse orbitale ne dépend pas de la masse du corps en orbite, c'est
fondamental.
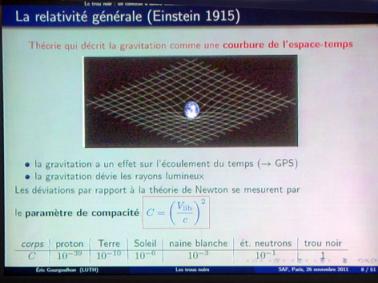
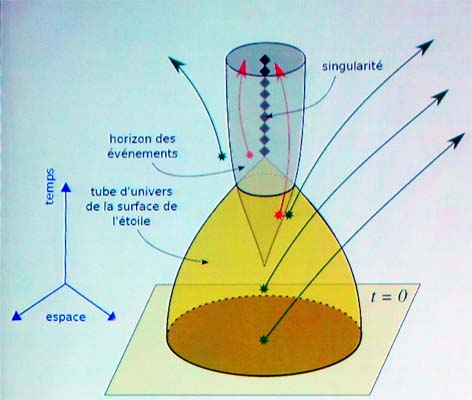 Un trou noir est une région de l’espace-temps d’où les
photons ne peuvent sortir.
Un trou noir est une région de l’espace-temps d’où les
photons ne peuvent sortir.
 Un trou noir est défini par seulement trois paramètres
:
Un trou noir est défini par seulement trois paramètres
: