Errors in the Steady State and Quasi-SS Models

Original par Ned Wright

www.astro.ucla.edu/~wright/cosmolog.htm

original de cet article : Errors in the Steady State and Quasi-SS Models: http://www.astro.ucla.edu/~wright/stdystat.htm<!DOCTYPE HTML PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN">

Les modèles "état ( quasi) stationnaire" SSC et QSSC et leurs problèmes

Le Modèle stationnaire a été inventé par les Anglais pour se persuader que l'Angleterre est éternelle. Les Anglais, qui sont un peuple peu mystique, ont inventé le cricket pour avoir une idée de ce qu'est l'éternité ( anonyme mais pas anglais ).

Le modèle état stationnaire pour l'Univers a été élaboré en 1948 par Bondi, Gold et Fred Hoyle. Bondi et Gold adoptèrent "le principe cosmologique parfait" et ajoutèrent l'hypothèse que l'Univers a toujours été le même de tout temps au principe d'homogénéité ( identique à lui même en tout lieu) et d'isotropie ( identique à lui même dans toutes les directions). A cette époque le modèle du Big bang était confronté au problème d'une prédiction de l'age de l'Univers manifestement trop courte lié à une mauvaise évaluation de la constante de Hubble ( air connu). Si l'Univers a été, est et restera le même alors la constante de Hubble est " constante" et v = dD/dt = HD a une solution exponentielle et le facteur d'échelle varie comme:

a(t) = exp(H(t_o-t))

De plus comme le rayon de courbure de l'Univers ne peut pas changer, mais doit augmenter, il ne peut être qu'infini. Donc le modèle état stationnaire a des sections spatiales "plates" comme dans le cas de densité critique dans le modèle Big bang. Comme l'expansion dilue la matière existante, mais que la densité doit rester constante ce modèle nécessite une création continue de matière. L'age moyen de la matière continuellement créée dans le modèle état stationnaire est <t> = 1/(3*H_o) mais certaines galaxies sont bien plus vieilles que la moyenne, ainsi les amas globulaires peuvent être intégrés si la voie lactée est plus vieille que la moyenne. Le diagramme d'espace temps ci dessous décrit le modèle "état stationnaire".

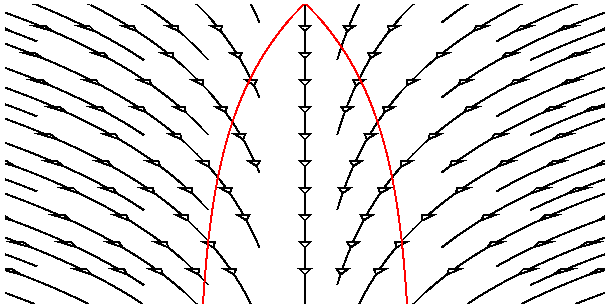
Notre cône de lumière du passé ( au centre) est représenté en rouge. Notons la création continuelle de Galaxies qui maintient la densité constante. Le modèle état stationnaire fait des prédictions précises. La première testée concerne le nombre de radio source faibles. Dans les années 50 les astronomes trouvèrent que les radiosources étaient typiquement plus lointaines que les galaxies typiques "optiques", donc une correction de la loi de comptage classique d'ordre cosmologique était escomptée. Pour le Big bang , la prédiction est que le nombre doit tomber en dessous de la loi habituelle correspondant à 8 fois plus de sources pour une limite quatre fois plus faible, d'un facteur approximativement égal à 1/(1+z)⁴ où z est le décalage spectral des sources. Cette loi stipule que les radio sources sont conservées, donc dans une région donnée de l'Univers, il y a tout le temps le même nombre de radio sources. Comme le volume de la région était plus petit dans le passé d'un facteur (1+z)³, la densité effective de radio sources était plus grande du même facteur. (1+z)³. La densité étant constante dans le modèle d'état stationnaire donc le facteur de correction de comptage doit être donné par 1/(1+z)⁷. Le diagramme ci dessous montre ce qui était escompté et ce qui est observé.

Le Big Bang prévoit un déficit de sources faibles, le modèle stationnaire prévoit un déficit encore plus important, mais les observations montrent un excédent de sources faibles. Le modèle stationnaire n'a pas de paramètres ajustables pour corriger cette différence, à la différence du Big Bang. L'hypothèse de conservation des radio sources peut être écartée au profit d'un excès de radio sources de 1 à 3 Giga années Lumières après le Big bang. Là où l'état stationnaire est en défaut, le Big Bang plus ouvert s'en sort en introduisant un nouveau paramètre pour décrire une nouvelle donnée.

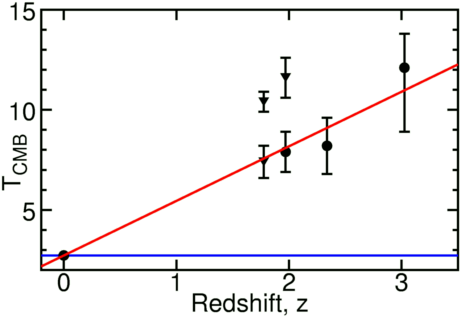
La découverte du rayonnement de fond cosmologique de type "corps noir"a sonné le glas du modèle stationnaire. L'Univers ne produit pas actuellement de rayonnement de type Corps noir, car il n'est pas isotherme et il est transparent et non pas opaque. De ce fait, comme dans le modèle stationnaire, l'Univers est toujours le même , il n'a pas pu générer ce rayonnement corps noir. Donc l'existence de ce rayonnement de fond thermique élimine la théorie de l'état stationnaire. De plus la température du RFC peut être mesurée dans des nuages très éloignés qui produisent des raies d'absorption dans le spectre d'émission des quasars. Les atomes de carbone neutre, dans ces nuages sont excités à une température d'excitation qui peut être mesurée par le rapport des raies. Ces températures d'excitation sont les limites supérieures des températures du RFC et sont montrées comme points triangulaires à droite. Dans certains nuages des corrections pour d'autres sources d'excitation peuvent être effectuées donnant une mesure directe de la température du RFC montrée par des points ronds. Ces données s'accordent très bien avec l'évolution prévue dans le modèle du Big bang: T_CMB = T_o(1+z), qui est représenté par la ligne rouge dans la figure. Même s'il y a un mécanisme inconnu qui produit un rayonnement de corps noir dans le modèle état stationnaire sa température serait indépendante du décalage spectral comme le montre la ligne bleue du diagramme, ce qui est infirmé par les observations, infirmant en conséquence ce modèle.

Le modèle Cosmologique quasi stationnaire est une tentative faite par Hoyle, Burbidge et Narlikar pour expliquer l'évolution de la température du RFC et le surplus de Radio sources faibles dans un Univers identique à lui même à longue échéance. Une modulation sinusoïdale est superposée à la croissance exponentielle du facteur d'échelle a(t). donnant un diagramme d'espace temps décrit ci dessous.

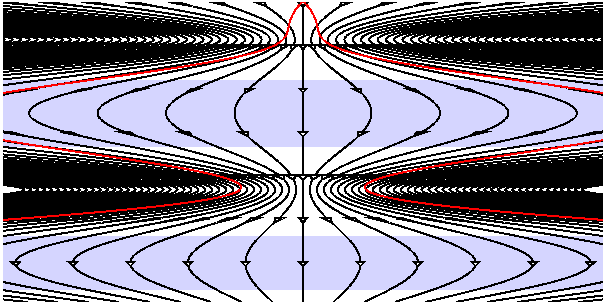
Pendant la longue phase précédente de l'Univers , notre cône du passé ( en rouge) était très grand, ce qui donnait un grand nombre de sources faibles. Malheureusement pour Hoyle, Burbidge et Narlikar ces sources devraient être décalées vers le bleu, comme indiqué par la couleur bleue sur le diagramme d'espace temps, et personne n'a jamais observé de radio-source faible décalée vers le bleu. Ces données disponibles avant que Hoyle, Burbidge et Narlikar publient leurs travaux disqualifient ce modèle élaboré pourtant des cosmologistes dont les travaux précédents avaient contribués à leur réputation.

Le Nouveau Modèle d'état quasi stationnaire

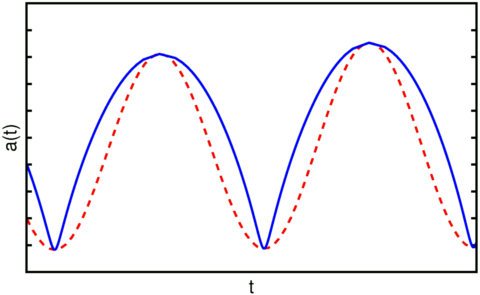
Hoyle, Burbidge et Narlikar n'ont pas abandonné leur modèle mais ont continué à le développer. Ils ont présenté dans une publication récente une nouvelle version plus proche de la physique standard. Dans ce modèle il y a un champ de création qui produit une densité d'énergie qui est négative de type rayonnement. Cette densité d'énergie négative devient prépondérante pour des décalages spectraux élevés et est la cause du rebond dans le modèle. La re-contraction qui conduit à la nature périodique est causée par la densité d'énergie négative du vide. Il en résulte une modulation du facteur d'échelle qui n'est plus une sinusoïde modulée par une exponentielle ( la courbe pointillée en rouge ), mais une fonction notoirement plus anguleuse montrée en bleu.

Ce qui suit comporte quelques passages qui peuvent paraître plutôt techniques aux astronomes qui n'ont pas trop de temps à consacrer à essayer de comprendre ce modèle. Comme la vitesse d'expansion tend vers zéro à a_min et a_max, et que la courbure est zéro, on peut facilement trouver une solution pour les trois densités associées, pour z_max=5 et a_max/a_min=(1+0.811)/(1-0.811) on trouve Omega_vac = -0.358, Omega_m = 1.623, et Omega_rad = -0.271. Ces paramètres conduisent à un paramètre de décélération q_o= 1.623/2+0.358-2*0.271 = 0.63.

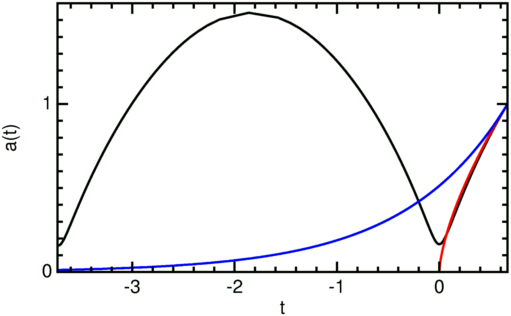
Comme ce paramètre de décélération est proche de la valeur de Einstein-de Sitter (EdS) de q_o = 0.5, il n'est pas surprenant que l'évolution du facteur d'échelle a(t) depuis le dernier minimum jusqu'à maintenant suit de près la courbe EdS. La figure à droite montre la courbe EdS en rouge et la courbe du modèle quasi stationnaire en bleu. Remarquons que le nouveau modèle quasi stationnaire n'accélère que pendant le rebond, ailleurs il décélère. Remarquons aussi que la densité de matière dans ce nouveau modèle est cinq fois plus grande que les estimations actuelles. L'unité pour l'axe des temps est 1/H_o, donc le temps écoulé depuis le dernier rebond pour ce nouveau modèle avec les paramètres choisis est le presque le exactement même que l'age de l'Univers, EdS: H_ot = 2/3.

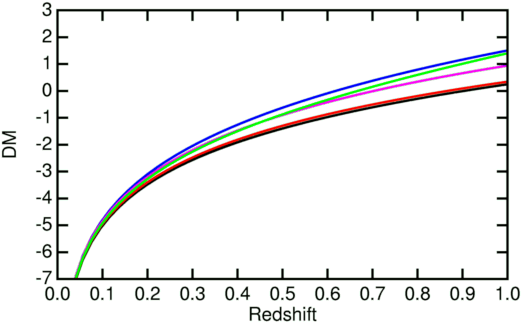
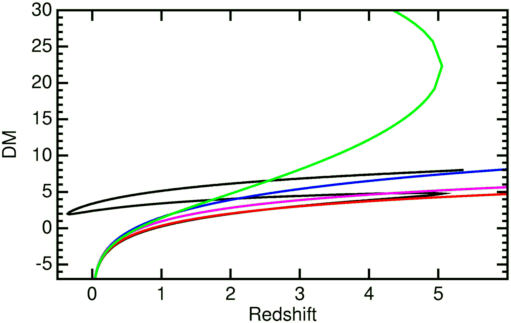
Si ce nouveau modèle décélère au lieu d'accélérer comment est ce possible comme le prétend Banerjee et al. (2000, AJ, 119, 2583) de respecter les mesures de distance des Supernovaes qui montrent une expansion accélérée ? La réponse repose sur l'extinction par les " filaments" du carbone et du fer que ce nouveau modèle utilise pour convertir la lumière des étoiles en photons du RFC. Comme le modèle a une décélération plus grande que le modèle EdS il nécessite beaucoup plus de poussière grise que le modèle ouvert et un peu plus que le modèle EdS considéré par Aguirre (1999, ApJL, 512, L19). La figure à droite montre le module de la distance ( DM) exprimé en unités c/H_o, DM = 5 log₁₀(D_L H_o/c), fonction du décalage spectral pour les modèles montrés sur la figure précédente. La courbe en rouge est le modèle EdS , celle en noir le Modèle quasi stationnaire sans absorption , celle en bleu le modèle stationnaire, celle en Magenta correspond au meilleur ajustement Omega_M=0.3 modèle plat dominé par le vide. La courbe en vert est le modèle quasi stationnaire avec un ordre de grandeur d' extinction par rayon de Hubble localement. La courbe verte coupe la courbe magenta à z = 0.45, ce qui est en bon accord avec les mesures sur les supernovaes. Mais Aguirre and Haiman (2000, ApJ, 532, 28) ont trouvé que le montant de poussière requis pour aller du modèle EdS aux observations des supernovaes n'est pas permis par les mesures sur le rayonnement de fond infra rouge ( Cosmic Infrared Background) donc le montant légèrement supérieur de poussière requis par le modèle quasi stationnaire est une hypothèse non valide.

A des décalages plus élevés l'extinction croît plutôt rapidement. Notons que l'équation (30) de Banerjee et al. qui donne l'extinction en fonction du décalage spectral est entaché d'une sérieuse erreur qui compromet la réponse à des décalages élevés. Mais en utilisant l'équation corrigée on obtient la courbe DM (z) comme montré sur la figure à droite. La courbe noire montre le QSSC sans extinction, montre le retour en arrière pour des faibles DM ( source plus brillantes) pendant le maximum précédent de a(t) ce que l'ancien QSSC utilisait pour expliquer l'excès de radiosources faibles. Mais avec la quantité de poussière requise pour se conformer aux mesures sur les supernovaes, l'extinction est si importante vers l'époque du minimum de taille qu'il est impossible de voir quoi que ce soit avant ce minimum. Dans le QSSC, l'opacité de la poussière dans la bande millimétrique est plus grande que dans la bande optique, donc l'Univers devrait être optiquement opaque à z=0.3 pour le RFC. Mais l'article préliminaire de Narlikar et al., qui calcule incorrectement les anisotropies fines du RFC, postule que l'univers est transparent jusqu'à z_max. Donc si Narlikar et al. a raison alors Banerjee et al. a tort et vice-versa. Ces articles ne peuvent pas être exacts ensembles puisque Banerjee et al. nécessite une opacité élevée alors que Narlikar et al. nécessite une faible opacité. En fait ils ont tort tous les deux. Ci joint la référence d'un document annoté marked up copy [384 kB] de Narlikar et al. relevant ses multiples erreurs. . Le modèle de Narlikar et al. devrait donner une anisotropie fine du RFC qui correspond à la transformation de Fourier de la fonction de corrélation à deux points des galaxies. Mais cette fonction de corrélation correspond à une loi en puissance , donc la puissance angulaire spectrale du RFC devrait être une loi en puissance et ne pas avoir de pic. Narlikar et al. Affirme juste qu'il doit y avoir un pic sans aucune référence ou justification.

La théorie de la nucléo-synthèse dans le QSSC prédisant l'abondance de l'hélium date des années 1960's, et s'appuie sur les huit repliements ou saveurs SU(3). Pour des raisons mystérieuses seuls des quarks up, down et strange sont produits . La suppression de saveur changeant le courant neutre signifie que tous les quarks strange se transforment en quarks up produisant un surplus important de protons par rapport aux neutrons. Mais si on admet l'existence des quarks charmed, ou de six saveurs de quarks, alors l'excès de protons se volatilise et on obtient un rapport H sur He incorrect dans les produits finaux.