Le modèle du big bang

Ce document est la reprise du document «  Le modèle du Big Bang » extrait de DEA CPM – Cosmologie -2001-2002 par Christophe Balland et Alain Bouquet

Les formules qui étaient peu lisibles ont été ré-écrites. On peut consulter l’original en : http://cdfinfo.in2p3.fr/Culture/Cosmologie/cosmodyn.html

J. Fric endosse l’entière responsabilité des erreurs que sa transcription aurait pu introduire.

[ Conservation énergie, Constante cosmologique, Domination matière, Domination poussière, Domination rayonnement, Entropie, Equation Friedman, Solution EE, Température.]

1 - L'équation de Friedmann

La métrique de Robertson-Walker

La théorie du Big-Bang repose sur les hypothèses suivantes :

· l'univers est – en première approximation – homogène et isotrope (principe cosmologique);

· sa structure métrique est déterminée par le contenu matériel de l’univers via l’équation d’Einstein de la relativité générale;

· la gravitation est – en première approximation – la seule force dominante à l’échelle cosmique.

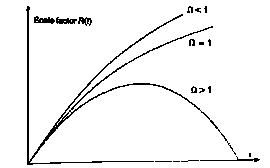
Friedmann montra en 1922 que cela conduit, pour un univers de courbure positive (univers fermé), à un univers en évolution, pouvant être soit en expansion soit en contraction. Si on extrapole dans le passé l’expansion actuellement observée, on en déduit l’existence d’une phase extrêmement dense, aboutissant à une singularité, le "big bang". En extrapolant dans le futur on aboutit aussi à une singularité, le "big crunch". L'univers est ainsi fermé dans le temps comme dans l'espace. Friedmann étudia en 1924 le cas d'une courbure négative (univers ouvert), qui possède une singularité dans le passé mais conduit à une expansion continuelle dans le futur. L'univers est ainsi ouvert dans le temps comme dans l'espace.

Sans connaître les travaux de Friedmann, Lemaître redécouvrit en 1925-1927 l'existence des solutions décrivant un univers en expansion. Plus au fait des observations astronomiques de l'époque (en particulier les observations de Slipher montrant que la plupart des "nébuleuses" avaient des décalages importants vers le rouge), il a relié ce mouvement de fuite des galaxies à une expansion générale de l'univers et donné une première estimation de la constante de Hubble : sa valeur voisine de 600 km/s/Mpc [la valeur estimée aujourd’hui est d’environ 70 km/s/Mpc] correspond dans un modèle simple à un âge de l'univers inférieur à 2x10⁹ ans, beaucoup trop jeune au vu des datations radioactives des roches donnant à la Terre un âge de 5x10⁹ ans. Lemaître utilisa donc la constante cosmologique introduite par Einstein pour "allonger" cet âge de l'univers. Il exploita aussi la découverte contemporaine de la mécanique quantique pour imaginer l'univers proche de la singularité comme un "Atome primordial". Comme Friedmann, il eut aussi quelque difficulté à faire admettre ses thèses, en particulier à Einstein et à Eddington que l'idée de commencement de l'univers révulsait. Lemaître a toujours soigneusement séparé ses convictions religieuses (il était prêtre) de ses travaux scientifiques, mais ses opposants ont souvent pratiqué un amalgame entre les deux.

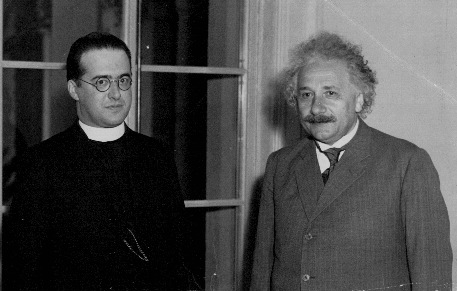
Georges Lemaître (avec Albert Einstein à droite)

Le principe cosmologique est une hypothèse si forte qu’elle suffit à déterminer la métrique de l’espace-temps. Cette métrique, due à Robertson et Walker, peut s'écrire :

ds² = g_mn dx^m dxⁿ = c² dt² - a²(t) [dr²/(1-kr²) + r²(dq² + sin²qdj²)]

Le "paramètre d'échelle" ou "facteur d’échelle" a(t) relie les coordonnées "comobiles" [r,q,j] à la distance physique des objets. Sa variation au cours du temps est déterminée par la théorie de la gravitation (la relativité générale est généralement choisie) et par le contenu matériel de l’univers à chaque instant (plus précisément par l’équation d’état de la matière).

Les solutions de l'équation d'Einstein

La cosmologie s'est longtemps limitée à rechercher des solutions de l’équation d'Einstein satisfaisant à la métrique de Robertson-Walker, c'est à dire trouver l'évolution du paramètre d'échelle a(t).

On part de l’équation d'Einstein qui relie le tenseur d'Einstein G^mn construit à partir de la métrique g_mn (et complété d'une éventuelle constante cosmologique L) à la distribution de matière décrite par le tenseur énergie-impulsion T^mn :

G^mn = R^mn - (1/2).R g^mn — L g^mn = 8 p G T^mn

La forme de la métrique de Robertson-Walker simplifie considérablement cette équation : les composantes G⁰ⁱ sont nulles de même que les composantes G^ij pour i ≠ j et les 3 composantes Gⁱⁱ sont identiques. Il n'y a donc que deux composantes à considérer, G⁰⁰ et Gⁱⁱ (et encore : elles sont reliées par l'identité de Bianchi qui traduit l'invariance par re- paramétrage de l'équation d'Einstein).

La métrique de Robertson-Walker correspond à un univers homogène empli d’un fluide parfait de densité r et de pression P, dont le tenseur énergie-impulsion est simplement:

T^mn = (r + P)V^mVⁿ - Pg^mn .

Ce fluide au repos (dans les coordonnées comobiles) a pour quadri-vitesse :

V^m = dx^m/ds =  [1, 0, 0, 0] .

Donc T⁰⁰ = r, T^ij = -P.g^ij et T⁰ⁱ  = 0.

Bien sûr, on retrouve les deux mêmes composantes pertinentes que pour le tenseur d'Einstein. La dérivée covariante du tenseur énergie-impulsion est nulle:

Ñ_m T^mn = 0 ce qui traduit la conservation locale de l'énergie.

La composante (00) de l’équation d'Einstein

que l'on écrit plus souvent sous la forme de Friedmann donne :

(a'/a)² = 8 p G r/3 -k/a² + L/3 {1}

C'est l'équation fondamentale de la cosmologie d'un univers homogène et isotrope, et elle permet de calculer l'évolution au cours du temps du paramètre d'échelle a(t). Sans aller plus loin, l'inspection de cette équation permet quelques remarques de grande portée :

· Le membre de gauche n'est pas autre chose que le carré de la constante de Hubble (constante dans l'espace mais non dans le temps) au temps t, H(t) = a'/a .

· Les trois termes du membre de droite dépendent différemment de a : la densité d'énergie r diminue rapidement quand a augmente [généralement comme 1/a³ ou 1/a₄], le terme de courbure spatiale k/a² diminue moins vite, et le terme constant L est… constant. Dans un univers où le paramètre d'échelle peut tendre vers zéro (modèles de big bang proprement dit), ce sont les termes de densité qui sont seuls importants à l'approche de cette singularité. Loin d'elle, le terme de courbure devient prédominant puis – éventuellement – le terme de constante cosmologique.

· Si la courbure est positive (k = +1) l'expansion peut s'arrêter, passer par un maximum (quand  a'= 0) avant de se transformer en contraction. Mais il peut aussi s'agir d'un minimum (une contraction devenant une expansion).

Revenons à l'équation d'Einstein. Les composantes (0,i) sont identiquement nulles de même que les composantes (i,j) pour i ≠j, et les composantes (ii) de l’équation d’Einstein donnent une seconde équation,

2a"/a + a’²/a² +k/a² -L = - 8GpP {2}

On peut combiner avec l’équation de Friedmann pour obtenir l’accélération :

a"/a = - (4Gp/3 ) ( r + 3p) + L/3

Cette équation, qui n'est rien d'autre que la trace de l'équation d'Einstein 2R + 2L = 8pG [r + 3P], a une interprétation Newtonnienne possible (quoique légèrement abusive), et je l'appellerai par la suite "l'équation de Newton".

En effet pour un univers empli de matière non relativiste la (densité d'énergie de la) pression est négligeable devant la densité d'énergie de masse, et le premier terme du membre de droite n'est pas autre chose que la masse M de matière dans une sphère de rayon a divisée par a² et multipliée par G, c'est donc l'accélération Newtonnienne d'une particule à la surface de cette sphère. Si on imagine que l'on a découpé cette sphère dans un univers euclidien infini, et que l'on considère comme nulle la contribution de la matière extérieure à la sphère à l'accélération de la particule (théorème de Newton, qui est ici utilisé en dehors de son domaine de validité), l'accélération gravitationnelle est bien celle que l'on obtiendrait en physique Newtonnienne. Quand au second terme du membre de droite, il décrit une répulsion dont l'intensité augmente linéairement avec la distance. Enfin, pour un gaz relativiste P = r/3 , et l'accélération est le double du cas non-relativiste : l'évolution d'un tel univers est donc plus rapide, comme nous le retrouverons plus loin.

On peut combiner les composantes (0,0) et (i,i) différemment en commençant par dériver par rapport au temps l’équation de Friedmann {1}, en oubliant L pour l’instant.

∂_t ([a'² + k = 8 p G a².r/3] → 2 a’.a’’ = 8 πG(ρ’.a²+2aa’ρ )/3

En reportant dans l’équation {2} qui définit la composante (i,i)

-8πGP =2a’’/a + (a’/a)² + k/a² = 8πG[ ρ’.a/a’ + 2ρ +ρ]/3

On obtient

- 3P = 3ρ + ρ’a/a’ → 3Pa’.a² + 3ρ’.a’.a² + ρ’.a³ = 0

Soit tout simplement :

- P.d(a³) + d(ρ.a³) = P.dV + dU = 0

Cette équation n'est autre que la conservation de l'énergie ! L'univers n'échange pas de chaleur avec l'extérieur. Si on se rappelle que dU = TdS - PdV , on obtient dS = 0 . L'expansion de l'univers est adiabatique et son entropie S totale reste conservée. Nous y reviendrons.

Et avec une constante cosmologique ? Elle se comporte comme un fluide de densité constante rV = L/(8pG) et de pression négative PV = -rV .

Pour elle : P dV + dU ≡  0.

2 - Solutions simples

Pour résoudre l’équation de Friedmann ou "l'équation de Newton", une équation d'état est nécessaire pour relier pression et densité et on peut l'obtenir, par exemple, à partir de la conservation de l'énergie dU + PdV = 0.

Trois cas limites sont intéressants:

1) constante cosmologique (ou densité d'énergie du "vide") où P = - r = Cte.

2) matière non-relativiste ( appelée "poussière") où la pression est négligeable devant la densité ® r ~ 1/a3.

3) matière relativiste (ou "rayonnement") où P = r/3 ® r ~ 1/a4.

Domination d'une constante cosmologique

Ce cas (alors considéré comme un univers statique) a été étudié par de Sitter dès 1917, avec k = +1 , L > 0 et r = 0 (univers vide de courbure spatiale positive).

L’équation de Friedmann s'intègre alors facilement :

a(t) = (H^-1) cosh { H.t } avec H² = L/3

Il n'y a pas de singularité dans un tel modèle puisque a(t) ne s'annule pas. Cet univers est spatialement fermé mais ouvert dans le temps. Remarquons que le paramètre d'échelle a(t) passe par une valeur minimale a_min = H^-1 et par suite le redshift passe par une valeur maximale (la constante arrête la contraction et fait "rebondir" l’univers). Les redshifts observés impliquent alors une borne supérieure sur la valeur de la constante cosmologique de l'ordre de H0² (H0 étant la valeur actuelle de la constante de Hubble).

Le cas k = +1 avec L < 0 est impossible, tandis que la situation k = -1 avec L < 0 décrit un univers spatialement ouvert mais fermé dans le temps, où le paramètre d'échelle donné par a(t) = (H^-1). cos{H t}, avec cette fois H² = -L/3, s'annule au temps t = ±H^-1/2p Enfin, le cas k = -1 et L > 0 est un univers en accélération permanente.

Ce sont aussi les solutions k = ±1 et L > 0 que l'on retrouve dans la théorie de l’état stationnaire proposée par Hoyle, Bondi et Gold. Dans ce modèle en effet, l'univers a une densité d'énergie r constante et une pression négligeable. D’autre part, cet univers de « de Sitter » est important dans le contexte de l'inflation où l’univers est supposé avoir été dominé — brièvement, et à une époque reculée — par une importante constante cosmologique.

Enfin, les résultats récents sur les supernovae lointaines indiqueraient que, dans l'équation de Friedmann, les contributions du terme de densité 8pGr/3, du terme de courbure k/a² et la constante cosmologique L seraient aujourd'hui du même ordre de grandeur. En ce cas la constante cosmologique dominera bientôt l'expansion de l'univers.

Domination de la matière non-relativiste

Pour la matière non-relativiste, la pression est négligeable en comparaison de la densité d'énergie (essentiellement la masse des particules) et l'équation dU + PdV = 0 se réduit à d(ra³) = 0 . Autrement dit, r(t) µ 1/a³(t) . Dans ce cas, le terme de courbure k/a² et la constante cosmologique sont négligeables devant la densité d’énergie quand a ® 0 et l'équation de Friedmann se résout immédiatement :

Þ a(t) µ t^2/3

Ce serait encore la situation actuelle, si le terme de courbure et la constante cosmologique étaient négligeables.

A partir de l’équation de Friedmann, on définit une densité critique rc ® 3H²/8pG, correspondant à un univers spatialement plat (k=0) et sans constante cosmologique (L=0). On définit aussi W comme le rapport r/rc de la densité réelle à la densité critique. En l’absence de constante cosmologique, k = 1 ¤ W > 1 et k = - 1 ¤ W < 1.

Numériquement, rc ~ 2.10^-29 h² g/cm3 (h = H0 / 100 km/s/Mpc). La densité moyenne de l'univers est une question non résolue : si la densité de matière sous forme d’étoiles (r- étoiles) ne semble pas dépasser 10-32 g/cm3, il semble y avoir 10 à 100 fois plus de matière sombre que de matière lumineuse.

L'équation de Friedmann se résout sous forme paramétrique :

A = a_max (1-cos h)/2, t = a_max (h -sin h)/2 pour k = 1,

et

a = a_max (cosh h - 1)/2, t=a_max (sinhh - h)/2 pour k = - 1

Pour h<<1, on retrouve a(t) µ t^2/3 car la courbure est négligeable. Puisque pour k = 1, 0 < h < 2p , une taille maximale a-max est atteinte pour h = p à t-max = a-max. L’univers se re-contracte ensuite et on retrouve a = 0 au temps t- Big-Crunch = 2. Tmax. Pour k = - 1, 0 < h < ∞ et a-max est un paramètre qui n’a plus le sens d’un rayon maximal. Pour h ® 2p , a(t) µ t car l’univers est quasiment vide et la gravitation ne freine plus l’expansion.

Domination du rayonnement

Pour la matière relativiste (génériquement appelée rayonnement), la pression P = r/3 et l'équation de conservation de l'énergie dU + PdV = 0 s'écrit :

d(ra³) + d(a³) = 0 Þ = r(t) µ a^-4

Ce n'est pas très surprenant : la densité numérique de particules relativistes décroît en 1/a³, tandis que leur énergie individuelle décroît en 1/a (pensons au redshift des photons pour qui l µ a et donc hn µ 1/a). Caveat : on suppose implicitement ici que ces particules relativistes ne sont ni créées ni détruites.

L'équation de Friedmann se résout alors immédiatement quand le terme de courbure k/a² et la constante cosmologique sont négligeables devant la densité d’énergie (en particulier quand a ® 0 )

Þ a(t) µ t^1/2

La densité d'énergie dans le rayonnement à 2.73 K est aujourd'hui r.g ~4.4.10^-34 g/cm³, ce qui est négligeable devant r-étoiles et correspond environ à 3.10⁹ photons par nucléon. La densité d’énergie dans le rayonnement des étoiles est beaucoup plus faible encore. Mais comme rg µ a^-4, domine r-matière (µ a^-3) et r-vide (constante) quand a ® 0, l'univers fut dominé par le rayonnement pendant 100 000 ans, environ. Le moment z_eq où matière et rayonnement contribuaient également se calcule simplement en écrivant r.g₀ [1+z_eq]⁴ = rmatière₀[1+z_eq]³ ce qui donne z_eq = 25 000 W-matière.h².

3 - Questions de température

L'expansion est donc adiabatique, ce qui fournit une relation entre la température T et le paramètre d'échelle a. Les règles habituelles de la thermodynamique nous permettent d'écrire pour une transformation adiabatique T ~ V1-g où T est la température, V le volume et g le rapport des chaleurs spécifiques. Pour un gaz parfait non-relativiste, g = 5/3, tandis que pour un gaz relativiste (des photons par exemple) g = 4/3 . Cela nous donne la relation entre température et paramètre d'échelle :

· pour un gaz non-relativiste T µ a^-2

· pour un gaz relativiste T µ a^-1

On se souvient que les vitesses particulières v des objets (particules ou galaxies) diminuent comme v ~ 1/a au cours de l'expansion. La température du gaz étant reliée à ces vitesses par 3kT/2 = mv²/2 , on retrouve bien T µ a^-2 pour un gaz non-relativiste. Quant au gaz relativiste, sa densité d'énergie est proportionnelle à T⁴ selon la loi de Stefan, et elle décroît bien comme 1/a⁴ pendant l'expansion.

Cela implique que la température de l'univers augmente à l'infini quand a ® 0 .

Le big bang est un big bang chaud !

Lemaître avait bien réalisé que l'état de densité très élevé qu'il imaginait (le big bang) devait être un état très chaud, mais les aspects thermodynamiques du big bang n'ont été élaborés qu'ensuite dans les années 30 (par Tolman en particulier) et c'est Gamow qui a compris toutes les conséquences d'un big bang chaud. Il a en effet saisi que la température moyenne de l'univers pouvait avoir dépassé le seuil des réactions thermonucléaires, et qu'un univers initialement composé uniquement de nucléons avait pu engendrer des noyaux plus lourds. Seulement, on sait aujourd'hui (grâce aux travaux de Hoyle, Fowler, Burbidge et Burbidge) que cette nucléosynthèse primordiale ne peut aller plus loin que le lithium, et que les noyaux plus lourds sont synthétisés dans les étoiles.

La notion de température suppose d'abord qu'il existe un équilibre thermodynamique entre particules, et donc que le taux d'interaction entre ces particules soit assez rapide pour l'assurer (compte tenu du temps limité dont on dispose et de l'expansion qui dilue ces particules). Différentes populations de particules peuvent fort bien être en équilibre thermique interne (et avoir ainsi une température bien définie) mais ne pas être en équilibre entre elles (et avoir donc des températures différentes). De quoi parle-t-on alors quand on parle de "la" température de l'univers ?

Il se trouve (hasard ?) que les interactions connues entre particules (électromagnétique, forte et faible) assurent un équilibre thermodynamique entre quarks, leptons et bosons de jauge à des températures "suffisamment hautes". Un équilibre thermique global existe ainsi pendant la première seconde de l'histoire de l'univers dans le modèle du big bang. Quand cet équilibre cesse d'être assuré, les particules désormais "découplées" vivent leur vie indépendamment des autres, et leurs températures évoluent indépendamment. On a ainsi plusieurs températures aujourd'hui : les photons sont à T ~ 2.7 K, les neutrinos à T ~ 2 K, les baryons à des températures allant de quelques K (gaz interstellaire froid) à quelques millions de K (centre des étoiles), etc.

Il existe donc une époque où la matière non-relativiste (des baryons et des électrons par exemple) est couplée au rayonnement (les photons par exemple). Qui fixe la variation de leur température commune avec le paramètre d'échelle ? Il se trouve (hasard ?) que les photons sont beaucoup plus nombreux que les baryons et les électrons, environ 10⁹ fois plus nombreux, et que ce sont eux qui fixent la température. En fait, l’observation indique que l’essentiel de l'entropie S de l’univers se trouve dans le rayonnement cosmologique à 2.7 K. Comme la densité d’entropie du rayonnement d’un corps noir varie comme T³, on retrouve encore :

S µ a³ T³ = constante Þ T(t) µ 1/a(t)

Parenthèse : on peut s'inquiéter à bon droit d'un modèle de big bang dans lequel l'entropie est conservée, alors que notre entourage manifeste une forte tendance à voir son entropie croître. En fait les processus irréversibles qui nous entourent augmentent l'entropie, mais cette augmentation est négligeable en comparaison de l'entropie "stockée" dans le rayonnement cosmologique à 2.7 K, puisque celle-ci correspond à une entropie par baryon de l'ordre de 10⁹ alors qu'elle est d'ordre 1 pour les processus thermodynamiques courants. D'autre part, le second principe de la thermodynamique qui stipule l'augmentation d'entropie des systèmes isolés est d'application délicate pour un système gravitationnel dont la chaleur spécifique est négative (un nuage de gaz qui se contracte gravitationnellement fait spontanément apparaître des gradients de densité et de température).

La densité numérique d’un gaz de particules de masse nulle à la température T est donnée par:

n(T) = 1/2p² òk².dk/ (e^k/T ± 1)= g [z(3)/p²].T ³

Le signe + au dénominateur correspond à la statistique de Fermi-Dirac et le signe — à celle de Bose-Einstein. Le coefficient g vaut 1 pour chaque degré de liberté d’un boson, mais seulement 3/4 pour un fermion en raison du changement de signe dans le dénominateur de l’intégrale, et z(3) = 1.202. La densité d’énergie est donnée par:

r(T) = 1/2p² òk³.dk/ (e^k/T ± 1)= g' [p²/30].T ⁴

Le coefficient g’ vaut 1 pour chaque degré de liberté d’un boson et 7/8 pour un fermion. On retrouve la loi de Stefan-Boltzmann en tenant compte des 2 degrés de liberté du photon. Si le rayonnement est formé de plusieurs types de bosons et de fermions (éventuellement à des températures différentes Ti) on peut écrire:

r(T) = = g_eff(T)(p²/30) T ⁴ où g_eff = S g'i [Ti/T]⁴

Enfin l’entropie dans un volume a³ s’estime simplement à partir de la relation:

TdS = dU + PdV = [r +r/3]a³ Þ S = (2p²/45)g’ a³ T³

Pour une population de fermions et de bosons, la densité d’entropie est donnée par:

s(T) = h_eff(T)(2p²/45) T ³ où h_eff = S g'i [Ti/T]³

Si toutes les particules ont la même température, h_eff = g_eff, mais cela cesse d’être vrai s’il existe des populations de températures différentes. C’est précisément le cas aujourd’hui, où les neutrinos sont plus froids que les photons.

Appliquons cela à l’expansion de l’univers. Les distances augmentent au cours du temps du facteur d’expansion a(t), les volumes augmentent comme a³, et il est pratique de définir le covolume comme le volume divisé par a³. L’expansion est adiabatique, ce qui implique que T µ 1/a, tant que h_eff ne change pas. Le nombre de particules par co-volume (la co-densité) reste ainsi constant au cours de l’expansion. Mais la relation entre T et a doit être réajustée chaque fois que des particules deviennent non relativistes ou s’annihilent.

Les notions précédentes s’étendent à des particules massives en introduisant les degrés de liberté effectifs. L’intégrale en impulsion fait alors intervenir la masse m des particules, et la densité d’énergie s’écrit alors:

r(T) = g_eff(m/T)( p²/30).T ⁴

Bien sûr g_eff(0) = 1 (ou 7/8), et g_eff(m/T) ® 0 pour m >> T. Plus précisément, l’intégrale peut se calculer comme une série de fonctions de Bessel (la série converge vite, heureusement), et on trouve pour m >> T:

n » [ mT/2p]^3/2 exp{-m/T} et r » n m

Si on a plusieurs types de bosons et de fermions, on somme sur tous les degrés de liberté effectifs. Le nombre de degrés de liberté effectifs diminue quand la température baisse, au fur et à mesure que les particules les plus massives cessent d’être relativistes.

Dans le modèle standard SU(3)xSU(2)xU(1), g_eff(T) passe de 427/4 pour T>M_W (12 bosons de jauge, 24 quarks et leptons et un doublet de Higgs) à 29/4 pour T<m_e . Un saut brutal se passe lors de la transition quarks-hadrons vers 250 MeV, quand les quarks u et d et les gluons (g_eff = 37) sont remplacés par les pions (g_eff = 3). La situation est évidemment la même pour une extension du modèle standard tant qu’on est en dessous de la plus légère des particules supplémentaires.

Brève histoire du temps

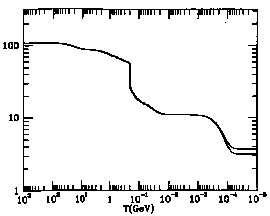
Connaissant maintenant les relations entre température T, paramètre d’échelle a (ou redshift z) et temps cosmique t, on peut reconstituer une histoire thermique de l’univers, dont les grandes lignes sont données dans le diagramme suivant:

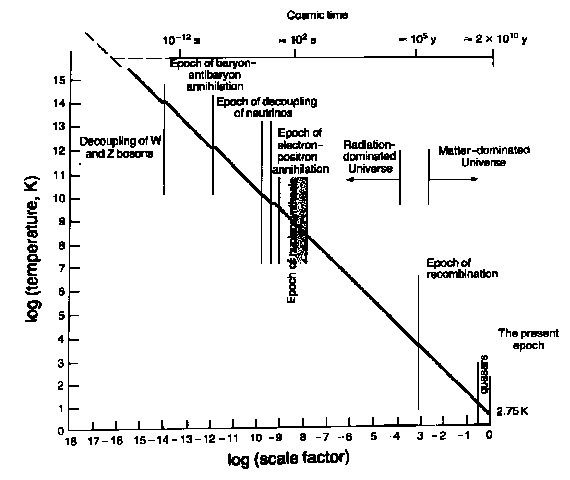
La température des photons décroît en 1/a, sauf lorsqu’elle est ralentie par l’injection de l’énergie libérée par la disparition de particules par annihilation (baryon-antibaryon, électrons-positrons…).

4 - Rayon et âge d’un univers de Friedmann

Peut-on estimer le "rayon de l'univers" aujourd'hui a0 et l’expansion maximale amax? En supposant nulle la constante cosmologique, l'équation de Friedmann a la forme:

H₀² = (8pG/3).rc. W₀ - k/a₀² = H₀² W₀ - k/a₀² Þ a0 = H₀ ^-1/ Ö[k.( W₀ -1)]

= 10¹⁰ h-1 années- lumières / Ö[k.( W₀ -1)]

L’expansion est maximale pour a =0, soit:

1/a_max²= (8pG/3).r_max = (8pG/3).r_0.(a₀/a_max)³= H₀² W_{0 .}(a₀/a_max)³ Þ a_max = H₀² W₀ a₀³

= .W₀)/H₀( W₀ -1)^3/2

Un rayon a correspond au temps t = H^-1 x f(W) où la fonction f(W) est:

f(W) = (W/2) (W - 1)^-3/2 [ cos^-1 ( 2/W - 1)] - 1/W - 1

On peut vérifier que f(W) < 2/3 pour W > 1. L’observation indique que W₀ < 2 ce qui implique t0 > H₀^-1[p/2-1] (environ 0.57 H₀^-1). Dans le cas d’un univers k = - 1, on retrouve t = H^-1 f(W) où la fonction f(W) est cette fois comprise entre 2/3 et 1. Pour W₀ ® 0, t0 ®H₀^-1, pour W₀ = 1, t0 = (2/3) H₀^-1, et pour W₀ >> 1, t0 << H₀^-1. Si la densité d'énergie est essentiellement due au rayonnement, le facteur 2/3 ® 1/2 .

Paramètres cosmologiques

Pour étudier la physique du Big-Bang, il nous faut connaître l’état actuel de l’univers pour remonter le temps en s’appuyant sur les lois de la physique. Cet état est essentiellement caractérisé par:

1) l’âge actuel t₀ de l’univers

2) la vitesse d’expansion locale H₀ = a'/a

3) la densité actuelle W₀ = 8pG r₀/3H₀²

4) le paramètre de décélération q₀ = - a".a/a'² mesurant le changement de H au cours du temps.

5) la constante cosmologique l0 º L/3H₀²

Les paramètres q₀ et l₀ n’ayant de conséquence qu’à grande distance et pour des temps anciens, l’évolution des objets observés et les biais observationnels compliquent leur mesure. Les meilleures estimations viennent des relations avec les autres paramètres dans le modèle de Friedmann, puisque:

(a'/a)² = 8 p G r/3 -k/a² + L/3 Þ l₀ = 1 - W₀ + k/a²H₀²

a"/a = - (4Gp/3 ) ( r + 3p) + L/3 Þ q₀ = W/2 - l₀

Recombinaison, équilibre matière-rayonnement

Une fois connus les paramètres actuels de l'univers, ou du moins une fois l'incertitude camouflée dans des coefficients h et W, nous pouvons reconstruire le passé de l'univers, ou prédire son avenir, à partir des équations de Friedmann, et d'un peu de physique atomique et nucléaire. Une fois le cadre des températures, densités, vitesses d'expansion, établi pour les différentes époques, on peut s'intéresser de plus près à la physique qui s'y déroule.

Age de l’univers

Il existe plusieurs manières d'estimer l'âge de l'univers:

1) Utiliser des marqueurs radioactifs (l'analogue du ¹⁴C), généralement des isotopes de l'uranium et du thorium produits en proportion calculable dans l'explosion des supernovas. La proportion relative de ces isotopes varie au cours du temps et Fowler estime ainsi à 10 milliards d'années l'époque de formation des plus anciens. Il faut y ajouter la durée de formation et d'évolution de l'étoile génitrice, ce qui aboutit à un univers vieux d’au moins 11 milliards d'années.

2) Utiliser les amas globulaires de notre galaxie. Les étoiles de ces amas sont les plus anciennes (ce qu'indique leur composition chimique) et les modèles d'évolution stellaire leur attribuent un âge de 16±2 milliards d'années.

3) Utiliser l’absence apparente de naines blanches de luminosité inférieure à 3.10^-5 LO dans le disque de notre Galaxie. Cette absence signifie que les naines blanches n’ont pas eu le temps de se refroidir en dessous de cette valeur, et donne au disque un âge maximal de (10±2) milliards d’années.

4) Utiliser le modèle du Big-Bang: t₀ = H₀^-1.f(W0) , où la fonction f(W) est toujours plus petite que 1, comme on l’a vu, et on obtient ainsi t₀ < 3.10¹⁷ h^-1 s (10 h^-1 milliards d'années).

Les différentes manières de déterminer l'âge de l'univers concordent, ce qui renforce l'idée de Big-Bang, mais tout juste! Si la constante de Hubble s'avérait proche de 100 km/s/Mpc (h » 1), un univers spatialement plat serait exclu en l’absence de constante cosmologique L.

Vitesse d'expansion de l'univers

La mesure de la valeur actuelle H₀ de la constante de Hubble se fait en principe en mesurant le redshift z de galaxies à des distances D de plus en plus grandes, et en optimisant la relation z = H₀.D. Mais il y a deux sources d'incertitudes:

- Le redshift n'est pas entièrement d'origine cosmologique, les galaxies ayant des mouvements propres, parfois importants ("chute virgocentrique", "grand attracteur"). Il faut donc utiliser des sources lointaines pour que le mouvement propre ne soit qu’une petite fraction du flux de Hubble. De plus un décalage gravitationnel peut se superposer dans le cas d'une source très massive.

- La distance de galaxies lointaines est mesurée de manière indirecte, par des méthodes plus ou moins fiables, calibrées sur les galaxies proches où des céphéides sont observées, et les résultats divergents:

<TBODY> Méthode	H0
Tully-Fisher (Luminosité absolue des spirales µ [Vitesse de rotation] ^4)	84 ± 10
Jacoby (Fonction de luminosité des nébuleuses planétaires supposée universelle)	80 ± 10
Tonry (Granularité apparente de la surface d’une galaxie µ 1/Distance^2)	80 ± 10
Supernovas de type I (explosion d’une naine blanche atteignant la masse de Chandrasekhar)	60 ± 15
Supernovas de type II (explosion d’une étoile massive)	60 ± 10
Relation de Vaucouleurs entre luminosité et nombre d’amas globulaires	85 ± 4
Décalage temporel entre images dédoublées par effet de lentille gravitationnelle	de 15 à 80 </TBODY>

L’incertitude sur la valeur actuelle de H₀ est intégrée dans les équations de la cosmologie en écrivant H₀ = 100 h. km/s/Mpc, avec un paramètre 0.4 < h < 1. Le temps de Hubble est alors : H₀^-1 = 3.10¹⁷ h^-1 s = 10¹⁰ h^-1 ans. Enfin, la valeur de la constante de Hubble fixe la valeur de la densité critique, celle d'un univers spatialement plat sans constante cosmologique: r_c º 3H₀²/8pG = 2.10^-29 h² g/cm³.

Densité de l'univers

Faisons l’inventaire du contenu de l’univers, en définissant Wi º r_i/r_c .

Rayonnement

Le rayonnement cosmologique est un rayonnement de corps noir à la température de 2,73 K, et sa densité d'énergie r_g est donnée par la loi de Stefan:

r_g = p²T⁴ /15 = 4,4.10^-34 [T/2,73K]⁴ g/cm³ Þ Wg = 2,2.10^-5 h^-2

Les autres sources de rayonnement électromagnétique sont négligeables en comparaison: que ce soient les radiosources, les étoiles (rayonnement visible, infrarouge ou ultraviolet), les sources de rayons X ou g, la densité d'énergie de leur rayonnement n'est qu'une petite fraction du rayonnement cosmologique. La luminosité moyenne du ciel est voisine de 2.1.10^-10 h L_O/pc³, ce qui donne une limite r_starlight < 10^-35 g/cm³ sur la densité d’énergie du rayonnement stellaire. Le rayonnement comprend toutes les particules ultra relativistes, et donc les neutrinos si ceux-ci ont une masse nulle. Chaque famille contribue de:

r_n = (p²/15)(7/8)T⁴ = 1.10^-34 [T/1,95K]⁴ g/cm3 Þ Wn = 5,3.10^-6 h^-2

Le facteur 7/8 vient, comme nous le verrons, de la différence entre les statistiques de Fermi-Dirac et de Bose-Einstein, et les neutrinos ont une température plus basse que les photons, car ces derniers ont été réchauffés par l’annihilation e+e- à une époque où les neutrinos étaient déjà découplés. Il n'est pas exclu que d’autres particules ultra relativistes soient aujourd'hui présentes en grand nombre et contribuent à la densité d'énergie de l'univers, mais on n'en a aucune indication observationnelle.

Matière non relativiste

La masse contenue dans les étoiles est estimée à partir du rayonnement de ces étoiles via un modèle d'évolution stellaire. La densité correspondante, moyennée sur le volume observé, est:

r_étoiles » 10^-32 g/cm³ Þ W_étoiles » 0.003 h^-2

La quantité de matière sous forme de gaz (surtout de l'hydrogène) interstellaire est plus faible (cela se voit par l'intensité des raies d'absorption dans le spectre d'étoiles ou de galaxies lointaines).

Par contre, il semble y avoir beaucoup de matière non lumineuse. Par exemple, une galaxie spirale est en rotation dans son plan, ce qui assure son équilibre contre la force de gravitation. Mais la vitesse de rotation est bien plus élevée que ce qui est nécessaire pour équilibrer l’attraction gravitationnelle due à la seule matière lumineuse (gaz, étoiles, poussières). On estime ainsi qu'une galaxie spirale possède 10 fois plus de matière non lumineuse que de matière lumineuse. Un résultat semblable est obtenu pour les galaxies elliptiques, à partir de la dispersion de vitesse des étoiles qui est reliée au potentiel gravitationnel par le théorème du viriel. Les mouvements à grande échelle et la dynamique des amas de galaxies indiquent qu’à leur tour ceux-ci possèdent environ 5 à 10 fois plus de matière que n'en contiennent les galaxies. Par ailleurs, on n'a pas observé de décélération de l'expansion, ce qui implique que la densité actuelle n'est certainement pas très supérieure à la densité critique rc, au plus un facteur 2. On aboutit ainsi à:

r_matière = 2.10^-29 W_matière h² g/cm³ avec 0.1 < W_matière < 2

Egalité matière rayonnement

La densité d'énergie est actuellement dominée par la matière (particules non relativistes), mais comme r_mat µ a^-3 et r_ray µ a^-4, celui-ci l'emporte quand a ® 0, donc quand l'univers était plus jeune. Les deux densités sont équivalentes au temps t_eq, pour un redshift z_eq . Pour z<z_eq, l'univers est dominé par la matière et a(t) µ t^2/3 , tandis que pour z>z_eq, l'univers est dominé par le rayonnement et a(t) µ t^1/2. En utilisant le fait que z+1=a(t₀)/a(t), le "point d’équivalence" z_eq est donné par:

r_ray(z_eq) = r_ray(0) (z_eq+1)⁴ = r_mat(z_eq) = r_mat(0) (z_eq+1)³

Þ z_eq = [r_mat(0)/ r_ray(0)] - 1 = [ 2.10^-29 W h²g/cm³ / 7,4. 10^-34 g/cm³] - 1 » 25 000 W₀. h²

L'âge correspondant est donné par:

t_eq = t₀ (z_eq+1)^-3/2 = 5.10¹⁰ s W₀ ^-3/2 f(W₀) h^-4

et la température par:

T_eq = T₀ (z_eq+1) » 7.10⁴ K. W₀ h²

Ce n'est pas très éloigné de la température d'ionisation de l'hydrogène (13.6 eV » 1,5.10⁵ K). La "recombinaison" du plasma d'électrons et de protons en atomes d'hydrogène neutre a une conséquence astrophysique majeure: le libre parcours moyen des photons devient très grand et l'univers auparavant opaque au rayonnement devient brusquement transparent. Les photons émis à ce moment-là n'ont pratiquement plus aucune chance d'être absorbés par la suite et continuent donc de se propager depuis cette époque. Ils forment le fond de rayonnement à 2,73 K .

En fait l'univers est opaque tant qu’une fraction des atomes d’hydrogène est ionisée (»5%), et les photons les plus énergétiques (ceux de la queue de la distribution de Planck) cessent d’être ionisants à une température bien plus basse, aux environs de T_rec = 3300 K. Cette température est atteinte pour un redshift z_rec = T_rec/T0 - 1 » 1200 au temps:

t_rec = t₀ (z_rec+1)^-3/2 (environ 5.10¹² W₀^-1/2 h^-1 s).

5 - Tests cosmologiques

Le modèle du Big-Bang prédit certaines relations entre des quantités en principe observables comme les distances, les luminosités, les redshifts, les densités… et ces relations peuvent être vérifiées (ou prises en défaut) par l’observation: ce sont les tests cosmologiques. Une fois connue la dépendance en t du facteur d’échelle a(t), on peut calculer à quelle distance se trouve un objet observé avec un redshift z (supposé cosmologique). Par exemple pour un univers plat, sans constante cosmologique, et dominé par la matière, on a, en utilisant les relations

z + 1 = a(t₀)/a(t₁) = (t₀/t₁)^2/3 et t₀ = 2.H₀/3 :

D_propre(t₀) º a(t₀) Dc = a(t₀) ò ^t1_t0 dt/a(t) = 2 H₀^-1 [ 1 - 1 / Ö ( z +1) ] » H₀^-1 .z pour z << 1

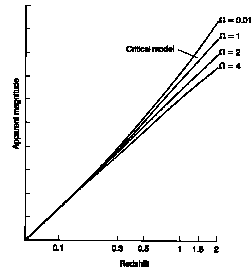
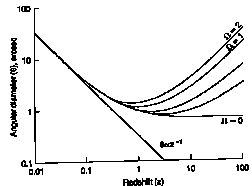
On retrouve bien sûr la loi de Hubble z » H₀.D_propre. On peut aussi tracer le diagramme de la luminosité apparente l (ou son logarithme la magnitude apparente m) en fonction du redshift (diagramme de Hubble), ou le diamètre apparent d en fonction du redshift. Si par exemple les galaxies ont toutes la même luminosité intrinsèque L ou le même diamètre intrinsèque d , elles doivent se répartir sur des courbes:

l = LH₀² / 16p( 1 + z)[ Ö(1+z) - 1 ]² ( µ z^-2 pour z << 1)

d = d H₀ / 2 [(1+z) ^-1 - (1+z)^{-3/2 ]} ( µ z^-1 pour z << 1)

dans un univers de "poussière", sans constante cosmologique ni courbure. Si la constante cosmologique ou la courbure ne sont pas négligeables, le résultat est un peu plus compliqué à obtenir. Confronter le résultat des observations à ces prédictions permet de tester le modèle cosmologique correspondant, ou la validité de l’hypothèse (discutable) que la luminosité ou le diamètre sont les mêmes en tout lieu et en tout temps.

Un autre test cosmologique consiste à compter le nombre de galaxies jusqu’à un redshift z: si leur densité co-mobile ne change pas au cours du temps (donc s’il ne naît pas de nouvelle galaxie et s’il n’en disparaît pas, par fusion par exemple), le nombre de galaxies observées devrait être proportionnel au volume co-mobile jusqu’au redshift z:

N(z) µ [D_propre(t₀)]³ µ H₀^-3 [ 1 - 1 / Ö(z+1)]³ ( µ z³ pour z << 1)

Mesurer le redshift d’un objet éloigné est très difficile car on en reçoit peu de photons, et on doit souvent se contenter de compter simplement le nombre d’objets N(l) jusqu’à une certaine luminosité apparente l au lieu d’un certain redshift z. En éliminant z, on obtient:

l/l₀ = 1 / (N/N₀)^1/3 [ 1 - (N/N₀)^1/3 ]

Ce test se révèle plus facile à effectuer, mais il est malheureusement beaucoup moins discriminant que les précédents.

6 - Inflation

Malgré ses succès remarquables, le modèle standard du Big-Bang possède des points inexpliqués. L'isotropie du rayonnement à 2,73K montre que l'univers est remarquablement uniforme, sur des distances qui, selon le modèle standard, ne sont pas causalement connectées. L'univers est pratiquement plat aujourd'hui, alors que la courbure augmente avec le temps. Enfin, la formation des galaxies par instabilité gravitationnelle nécessite des fluctuations de densité initiales suivant une distribution bien particulière, sans échelle, dite distribution de Zel'dovich. Tout cela semble résulter de conditions initiales particulièrement ad hoc, ce qui est très désagréable, et pour les expliquer on a eu recours aux effets quantiques de la gravitation, au principe anthropique ou à l'inflation, qui postule une période d'expansion ultrarapide au début du Big-Bang.

Paradoxes

L'univers nous apparaît quasiment plat et homogène, et ce fut le point de départ du modèle de Friedmann. Mais ce n'est pas "normal"…

Platitude

La densité moyenne de l'univers est aujourd'hui voisine de la densité critique bien que, selon le Big-Bang "standard", elle jamais cessé de s'en écarter. La courbure de l'univers aujourd'hui est inconnue, ce qui se traduit par 0.1 < W(t₀) < 2. Mais W(t) -1 augmente au cours du temps. L'équation de Friedmann s'écrit encore:

(8pG/3)r_c [W(t) - 1] = [a'(t)/a(t)]² [W(t) - 1] = k/a²(t)

Comme a(t)/a(t₀) = [t/t0]^a, avec a = 1/2 ou 2/3 selon le cas, on a:

W(t)-1 = [W(t₀)-1] [t/t₀]^2-2a

W(t)-1 augmente donc comme t^2/3 quand la matière domine, et comme t quand le rayonnement domine.

W(t₀) < 2 Þ W(t_eq) - 1 < 10^-5 Þ W(t_nucl) - 1 < 10^-15 Þ W(t_Planck) - 1 < 10^-59

La densité initiale devait donc être incroyablement proche de la densité critique pour qu'aujourd'hui encore on ne sache pas si l'univers est ouvert ou fermé. Une autre manière de présenter les choses est de dire que l'univers est "trop vieux": une courbure initiale positive "normale" aurait conduit depuis très longtemps au collapse final, une courbure négative à un univers beaucoup plus dilué que celui que l'on voit. Si au contraire l'expansion initiale se fait à densité constante, la densité critique se rapproche de la densité moyenne, ce qui expliquerait leur proximité actuelle. Ce n'est pas un problème mineur: une densité de un millionième supérieure à la densité critique une seconde après le Big-Bang, et l'univers se serait recontracté en moins d'un mois, une densité de un millionième inférieure, et l'univers serait si dilué qu'aucune étoile ne se serait formée.

Horizon

Les variations de température du rayonnement cosmologique sont si faibles d'un point du ciel à un autre qu'on n'a que des bornes supérieures. Et pourtant l'horizon au moment de son émission ne dépasse pas une dizaine de milliradians. En effet, sa taille angulaire est q = (Dc)1/(Dc)2 où (Dc)1 est la taille de l’horizon à la recombinaison (distance parcourue par un signal entre le Big-Bang et t_rec) et (Dc)2 la distance parcourue par les photons depuis la recombinaison, en coordonnées comobiles:

(Dc)1 = ò ^trec ₀ dt/a(t) = 2t_rec / a(t_rec)

(Dc)2 = ò ^t0 t_rec dt/a(t) = 3 t₀/a(t₀) on déduit de ces deux relations

q = (Dc)1 / (Dc)2 = 2 t_rec. a(t0) /3t₀.a(t_rec) = (2/3) (t_rec / t₀)^1/3 = 0,01 radian »1 degré

Il y a donc un problème de causalité: le rayonnement cosmologique présente la même température sur toute la surface du ciel. Or seules des régions de l'univers séparées de moins de 600 000 années-lumière au moment où ce rayonnement a été émis ont pu entrer en contact et uniformiser leurs températures. Or ces régions sont aujourd'hui séparées de moins de 1 degré sur la surface du ciel, et l'isotropie observée apparaît comme une coïncidence. Une expansion beaucoup plus rapide dans les premiers instants agrandirait ces régions, et la coïncidence n'en serait plus une.

Singularités topologiques

Les noeuds topologiques (murs, cordes, monopôles) sont reliés à ce problème de causalité. Pour s'en débarrasser, il faut que l'horizon au moment de leur formation soit beaucoup plus grand que dans le modèle standard, ou encore que l'univers se dilate considérablement après leur formation, les diluant de ce fait. Dans les deux cas, la probabilité d'en avoir un à proximité peut diminuer suffisamment.

Germes de galaxies

La formation des galaxies ne se fait pas à partir de n'importe quel type de fluctuations initiales. Harrison et Zel'dovich ont montré que le spectre (par décomposition de Fourier) ne devait pas présenter d'échelle intrinsèque. Cela peut être postulé comme condition initiale, mais une motivation physique est préférable.

Origine du Big-Bang

Enfin on peut se demander la cause du Big-Bang, c'est à dire ce qui cause l'expansion initiale (que la gravitation ne fait que ralentir). Une phase initiale de De Sitter supprime doublement le problème: l’univers n’a pas de commencement, et l’expansion y est accélérée…

Principe de l'inflation

L’idée fondamentale de l’inflation est qu’à un certain moment la densité d’énergie était dominée par une densité constante (celle du vide) et que l’expansion était alors exponentielle.

Repartons du lagrangien d’un champ scalaire j, sans préciser pour l’instant son identité:

L =(1/2). g^mn¶_mj ¶_nj - V(j)

qui conduit à l’équation du mouvement j " + 3 Hj' + ¶_jV(j) = 0 . Si le champ j n’est pas au minimum du potentiel, quel qu’en soit la raison (fluctuation, transition de phase…), il met un temps fini pour y parvenir, et durant tout ce temps la densité d’énergie du vide n’est pas nulle et peut entraîner une inflation.

Loin de l’équilibre, H est grand et l’évolution du champ j est lente et l’inflation perdure. Près de l’équilibre au contraire le champ oscille autour de la position d’équilibre, et l’énergie stockée dans ces oscillations est peu à peu transmise à toute particule à laquelle j est couplé, ce qui amortit les oscillations et réchauffe la particule en question (et en principe tout l’univers).

Tout marche bien si le potentiel V(j) a la bonne forme, un plateau assez long pour que l’inflation dure et un minimum assez creux pour que le réchauffage soit efficace. Le problème est maintenant d’identifier j. Initialement, il s’agissait du scalaire de Higgs d’une théorie de grande unification, mais les exigences de l’inflation sur la forme du potentiel se révèlent incompatibles avec les contraintes des GUT, en particulier son couplage doit être extrêmement faible. On invente alors un champ scalaire singulet de jauge, l’inflaton, dont le seul rôle est de permettre une inflation correcte (quitte à lui trouver ensuite une place dans un modèle unifiant).

On suppose soit que l'énergie du vide est nulle à l'équilibre mais que l'univers s'est trouvé momentanément hors d'équilibre au moment du Big-Bang (inflation "chaotique" de Linde), soit que l'équilibre varie avec la température au cours d’une transition de phase (inflation de Guth, modifiée par Steinhardt et Linde) et que son énergie diminue brutalement à un certain moment, signant la fin de l'inflation.

Aucun modèle d’inflation n’est réellement satisfaisant, mais comme elle explique les coïncidences de la version standard du Big-Bang, elle est aujourd'hui acceptée par la plupart des cosmologistes bien qu'il soit très difficile d'en construire un modèle explicite. Elle a également la précieuse qualité de pouvoir être réfutée, car elle prédit une densité moyenne de l'univers égale à la densité critique (à la précision des mesures près), et les mesures devraient s'améliorer suffisamment dans les années qui viennent pour que l'on sache si c'est bien le cas. Cela impliquerait d'ailleurs que les 9/10 de la matière de l'univers soit d'un type différent de celle que nous connaissons.

Le paradigme de l’inflation autorise un univers extrêmement inhomogène à très très grande échelle, et de plus la physique peut être très différentes dans différentes parties de l’univers (par exemple les brisures de symétrie peuvent y être différentes, telles que SU(5) ® SU(4).U(1)).

Résidus des brisures de symétrie

La brisure spontanée d'une symétrie au cours de l'expansion peut laisser derrière elle des résidus, des défauts topologiques, qui peuvent jouer un rôle très important dans l'évolution de l'univers.

Murs

Supposons qu'il existe un champ scalaire j dont le lagrangien L possède une symétrie discrète, une invariance sous j ® - j, par exemple:

L = (1/2)¶_mj ¶^mj + m² j² - (l/4)j⁴ - m⁴/4l

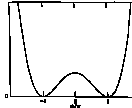
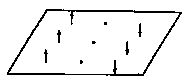
A haute température, un terme correctif de l’ordre de - lT²j²/8 s'ajoute à L, le minimum du potentiel se trouve à j = 0 et la symétrie j ® - j est intacte. Quand la température baisse en dessous d’une température "critique" Tc » 2m/l , la symétrie se brise spontanément, et le minimum se trouve à s = m/Öl, chacune des deux valeurs possibles ±s étant choisie aléatoirement.

Certaines régions de l'univers ont donc s comme "vide" pour le champ j, d'autres ont - s. Mais ces régions sont séparées par une zone où le champ j passe de - s à s. Dans cette zone le potentiel varie de zéro à zéro, mais en passant par la valeur m⁴/4l. Ce potentiel n'est pas autre chose qu'une densité d'énergie du point de vue gravitationnel

T_mn = ¶_mj¶_nj - L Þ T_mn = V(j)g_mn pour un champ constant

Le facteur de conversion 1 GeV⁴ = 2,3.10¹⁷ g/cm3 montre que cette densité d'énergie est colossale: la densité dans ce "mur" atteint W » 10⁴⁰ si l'échelle des masses est de l'ordre du GeV et le couplage de 0,1. Si un tel mur peut a priori être aussi grand que l’horizon au moment de la transition de phase qui lui donne naissance, son épaisseur est très faible. Elle est donnée par la résolution de l’équation du mouvement:

Dj = ¶V/¶j Þ j(z) = s th (m.z / Ö2 ) Þ Epaisseur = Ö2 / m » 3.10^-14 cm . 1 Gev / m ,

Masse / Surface = 2Ö2 m³ / 3l » 4000g/cm² ( m / 1 Gev )³

Ce mur est topologiquement stable, il peut se déplacer ou se déformer, mais ne peut disparaître que par annihilation avec un "anti-mur" (un mur dont les choix de minimum sont inversés de part et d’autre).

Toute symétrie discrète se brisant spontanément conduit à l'existence de semblables murs séparant les régions qui ont choisi une possibilité de celles qui ont choisi une autre. La taille de ces régions ne saurait être supérieure à la taille de l'horizon au moment de la brisure de la symétrie, ce qui permet de donner une valeur inférieure à la contribution de ces murs à la densité d'énergie de l'univers. Il y a toujours plusieurs dizaines d'ordres de grandeur d'excédent, et il faut soit modifier le modèle pour éviter la brisure de symétries discrètes, soit se débarrasser de ces murs (par inflation, par exemple).

Cordes

Les symétries continues conduisent aussi à des noeuds topologiques. Le cas le plus simple conduit aux cordes cosmiques (rien à voir avec les supercordes!), qui sont nettement plus acceptables, voire même désirables… Soit une théorie de jauge U(1) de Lagrangien:

L = D_mjD^mj† - (1/4).F_mnF^mn + (1/2)m² j†j - (l/4)(j†j)² - m⁴/4l

La symétrie U(1) est brisée spontanément, et le champ complexe jj prend une valeur moyenne dans le vide non nulle :

s = (m/Öl).e^-iq . Mais la direction q de la brisure dans le plan (j,j†) n’est pas déterminée et peut varier d’un point à un autre. La seule restriction est que j soit univalué, et pour cela il suffit que q varie d’un multiple entier de 2p le long de tout chemin fermé. S’il existe un chemin où q varie de 2p, il englobe nécessairement une région où j = 0. Cette région est donc un élément d’un tube de vide symétrique, ou "faux vide", qui est fermé ou infini (sinon le chemin pourrait être déformé pour sortir de la région où j = 0). Tout comme les murs, la dimension transversale ( » 1/m) est beaucoup plus petite que leur longueur ( » horizon), et on les appelle des cordes cosmiques.

L’énergie (la masse) d’une corde par unité de longueur est m » m²/l » 10^-9 g/cm (m/1 GeV)². Une corde grande comme l’horizon (10²⁸ cm) provenant d’une brisure de la symétrie de grande unification (m » 10¹⁶ GeV) aurait une masse M » 10⁵¹ g » 10¹⁷ MO (la masse d’un superamas).

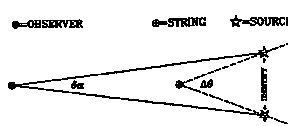
Les effets gravitationnels d’une telle corde sont très intéressants: l’espace-temps autour d’une corde est presque minkowskien, mais pas tout à fait. En coordonnées cylindriques [t,z,r,q], la coordonnée polaire est limitée à l’intervalle:

0 < q < 2p{1—4 [m/M_Planck]²}

Cette particularité conduit à des effets de lentille gravitationnelle, et aussi à des fluctuations dans le rayonnement à 2.73 K (une différence de température entre les 2 côtés de la corde). La non observation actuelle de telles fluctuations implique m < 10^-5 M_Planck². De plus une corde perturbe la distribution de matière dans son sillage, ce qui pourrait être un germe de galaxies: beaucoup d’études ont été consacrées à cette possibilité.

Monopôles

Les murs sont des défauts topologiques à 2 dimensions, les cordes à 1 dimension, mais il existe aussi des défauts topologiques à zéro dimension, des points. Ce sont des monopôles magnétiques. Le cas le plus simple utilise le groupe de jauge SO(3) et le Lagrangien:

L = D_mj^aD^mj^a - (1/4)F_mnF^mn + (1/2)m² j^aj^a - (l/8)(j^aj^a)²

qui conduit à une brisure spontanée de symétrie, et encore une fois seul le module de s^a est déterminé mais non son orientation (a) dans SO(3). Une solution en "oursin" est possible, où le champ de Higgs est de la forme s^a = |s|^r à grande distance (^r est le vecteur unité dans l’espace physique). Le champ j est nécessairement nul à l’origine et la configuration est topologiquement stable (on ne peut pas peigner une sphère). Le champ électromagnétique adopte alors une configuration telle que les lignes de champ magnétique rayonnent à partir de l’origine: d’où le nom de monopôle magnétique. La taille de ce monopôle est d’ordre 1/m et sa masse m_M est donc d’ordre m. Plus précisément, elle dépend de a et de l, et varie entre Ö(4p/al) . m = M_V/a et 1.8 fois cette valeur (M_V est la masse du boson de jauge massif qui apparaît après la brisure de symétrie).

L’existence de configurations topologiques stables n’est pas toujours possible. Si un groupe de symétrie G ® H lors de la brisure, il faut que l’application de la variété G/H sur la sphère soit non triviale. Cela est automatique s’il apparaît un facteur U(1) lors de la brisure. L’existence de monopôles magnétiques est donc une conséquence inévitable des théories de grande unification, dont l’échelle de masse m = M_GUT » 10¹⁶ GeV implique que ce sont des objets très lourds!

Cela a immédiatement des conséquences cosmologiques désastreuses. La brisure de la symétrie GUT ne peut pas être corrélée sur des distances plus grandes que la taille d_H de l’horizon à l’époque: le nombre de monopôles est donc n_M ® (1/d_H)³ » (M_GUT²/M_Planck)³. La densité de masse de ces monopôles serait alors actuellement:

r_M » m_M (M_GUT²/M_Planck)³ (T₀ /M_GUT)³ » (1/a)(M_GUT⁴T₀³ / M_Planck³ » 3.10^-13 g/cm³

à peine 16 ordres de grandeurs au-dessus de la densité critique… Il semble difficile que les monopôles s’annihilent assez vite avec des antimonopôles pour résoudre cette difficulté, et la meilleure solution semble le recours à l’inflation, qui dilate l’horizon au delà de l’univers visible.

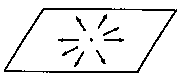
Textures

A la différence des murs, cordes et monopôles, une texture n’est pas topologiquement stable. C’est aussi une région de l’univers où la densité est un peu plus forte, mais à cause du terme de gradient cette fois, et non du potentiel:

dr = (¶_mj)² + V(j) » s² / t² » s² T⁴ / M_Planck²

Une texture se dénoue donc rapidement (comparé à l’âge de l’univers bien sûr), mais d’autres apparaissent continuellement:

L’intérêt vient de ce que l’on obtient naturellement un spectre "sans échelle" de Harrison-Zel’dovich:

dr/r » s² / M_Planck² » constante

Comme le souhaitent les fabricants de galaxies (et comme le prévoit aussi l’inflation). Mais à la différence de l’inflation, les spectres de fluctuation consécutifs à des brisures de symétrie ont une distribution non gaussienne de dr/r qui pourrait favoriser l’obtention de structures à très grande échelle (structures peut-être trop accentuées d’ailleurs…).

7 - Baryons et matière noire

Asymétrie matière-antimatière

Dans le modèle standard du Big-Bang, on a toujours trop ou pas assez de baryons. Appliquons en effet le calcul de la densité résiduelle aux nucléons. La section efficace est en ce cas de l'ordre de 10^-25 cm², et la température de découplage de l'ordre de 21 MeV (mp/T_dec » 45), ce qui conduirait à W_b. h² » 10^-11! On observe beaucoup plus de baryons que cela. Une asymétrie entre nucléons et antinucléons (un excès de nucléons pour être précis) doit donc être présente avant le découplage, de l’ordre de (n_B - n_B)/s » 10^-10_. On peut postuler cette asymétrie comme une condition initiale du Big-Bang, mais elle découle des théories de grande unification. Sakharov a indiqué dès 1967 les conditions nécessaires:

· Une théorie ne conservant pas le nombre baryonique (évidemment).

· Une théorie ne conservant pas C ni CP, sans quoi les réactions augmentant le nombre baryonique seraient exactement compensées par d'autres réactions le diminuant.

· Que ces réactions ne soient pas en équilibre thermique, sinon aucune asymétrie ne pourrait se développer.

Les théories de grande unification (GUT) remplissent les deux premières conditions, et l'expansion de l'univers permet aux réactions de sortir de l'équilibre (il arrive un moment où l'intervalle entre deux collisions changeant le nombre baryonique est plus grand que le temps de Hubble). L'asymétrie baryonique se développe dans le bref intervalle entre la sortie de l'équilibre et le moment où l'univers est trop froid pour que les réactions (qui utilisent les bosons super-lourds des GUT) se produisent encore. Il existe de nombreuses théories de grande unification concurrentes, et beaucoup de paramètres libres dans chacune, ce qui empêche une prédiction de l'asymétrie baryonique. Par contre, il est possible de reproduire l'asymétrie observée dans certains modèles (pas tous).

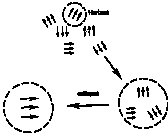
Le mécanisme principal est une désintégration de bosons super lourds X et X( bosons de jauge ou de Higgs , dont les couplages violent le nombre baryonique) X ® qq (rapport de branchement r) tandis que X ® qq avec un rapport de branchement r . La violation de C et de CP autorise r ¹ r ‚ . Si on a initialement autant de X que de X , ( ce qui est le cas en équilibre)une asymétrie apparaît lors de la désintégration:

(n_B - n_B) / s » (r - r )n_X/g_eff n _g »10^-10

La violation de CP requise semble faible (r - r »10^-8), mais en fait elle n’apparaît pas au 1° terme de la série de perturbations et il faut aller à 2 ou 3 boucles pour obtenir une contribution différente à G(X ® qq) et à G(X® qq ): par conséquent r - r » aⁿ avec n = 2 ou 3 au moins. Un corollaire est qu’il ne peut y avoir beaucoup d’entropie générée depuis la baryosynthèse.

La désintégration hors d’équilibre des bosons X et doit se faire à une température T << m_X (pour éviter les désintégrations inverses) mais avec une densité n_X » n_g pour générer une asymétrie suffisante. Le découplage des X doit donc se faire alors qu’ils sont ultra relativistes, ce qui donne une contrainte sur leur masse:

m_X > 10¹⁷ GeV [a / 0,1]

Pour les bosons de jauge, a » 0.1, mais le couplage de Yukawa des Higgs pourrait être plus faible et permettre une masse mX » 10¹⁵ GeV. Tant que les réactions sont en équilibre, non seulement aucune asymétrie n’est générée, mais toute asymétrie préexistante est effacée! La baryosynthèse due aux GUT génère donc la même asymétrie en tous les points de l’univers. Autrement dit il n’y a pas de fluctuation locale du nombre baryonique comparé au nombre de photons.

Plus récemment, on s'est rendu compte qu'il était possible qu'une asymétrie matière antimatière apparaisse dans le "modèle standard", sans grande unification. Le modèle lui-même traite symétriquement matière et antimatière, mais certaines configurations non triviales des champs de jauge (instantons, sphalérons) conduisent peut-être à cette asymétrie. Les calculs sont extrêmement délicats, et il n'y a pas encore accord général.

Nucléosynthèse et machos

On n'observe pas assez de baryons: la nucléosynthèse primordiale implique une densité moyenne de baryons supérieure à celle qui est observée dans les étoiles ou sous forme de nuages de gaz:

Nucléosynthèse Þ W_b h² = 0,01 ± 0,001 Observations Þ W_étoiles h² » 0,003

Si h = 0,5, il y a un désaccord d’un facteur 10. Où sont les baryons manquants? Il semble y avoir beaucoup de matière sombre dans l'univers: la dynamique des galaxies et des amas de galaxies indique que W est compris entre 0,1 et 1 (avec de grandes incertitudes), les scénarios de formation des galaxies sont meilleurs avec un W voisin de 1, et enfin l'inflation conduit à W = 1. Les baryons contribuent certainement à cette matière sombre, mais probablement pas à la totalité. Il y a plusieurs possibilités:

· une composante très diffuse, sous forme de gaz ionisé. Il manque le mécanisme qui ioniserait ce gaz (supernovas?), mais c’est une direction de recherche très active.

· des étoiles très peu lumineuses parce qu'elles sont trop légères pour que s'y allument les réactions thermonucléaires (naines brunes ou Jupiters). Elles devraient rayonner dans l’infrarouge (on les cherche), et également provoquer des effets de lentille gravitationnelle en passant devant une étoile plus éloignée. Deux expériences sont actuellement en cours pour détecter cet effet sur les étoiles du Grand Nuage de Magellan: on attend de l’ordre de 1 événement/million d’étoiles/an dans ce projet MACHO (MAssive Compact Halo Object).

· des étoiles presque éteintes (naines blanches) sont moins vraisemblables car elles auraient produit beaucoup trop d’élément lourds au cours de leur vie active (et seraient visibles dans les galaxies éloignées vues telles qu’elles étaient autrefois).

· des trous noirs de plusieurs centaines de masses solaires sont une possibilité encore ouverte (trop massifs pour avoir laissé échapper ces éléments lourds, trop légers pour perturber l’équilibre du disque galactique).

<TBODY> CNRS

IN2P3

CdF

PCC

Cosmologie

Matière noire

Agape

Supernovae

CMB

Temps </TBODY>