11

Trous Noirs en rotation chargés et leur thermodynamique

Retour au chapitre 3

Introduction

Les exemples cités ci dessous montrent que le calcul des équations décrivant les géodésiques dans la métrique de Kerr Newman, est en général assez laborieux.

On commencera par un calcul de géodésique polaire, puis on comparera à celui d’une géodésique équatoriale.

L’aspect répulsif de la singularité sera mis en évidence sur un cas très simple, lorsque le spin est nul, et dans le cas extrémal (Trou noir de Reissner Nordström extrémal).

On utilise souvent ces trous noirs chargés statiques pour étudier la phénoménologie des trous noirs de Kerr Newman, car du fait de leur symétrie sphérique, les calculs sont plus simples et ils présentent des similitudes certaines avec le Trou noir avec spin non nul ( en particulier deux horizons).

11.1 La Solution Kerr-Newman

Nous allons étudier les solutions pour les trous noirs en rotation chargés.

Soit :

La charge spécifique e liée à la charge q par:

(11.1.1)

Même si cela ne devrait pas se faire, le moment angulaire spécifique "a" est utilisé quelquefois comme synonyme du paramètre de Rotation. Le paramètre de rotation devrait être exclusivement réservé pour désigner la quantité ac²/GM. Le moment angulaire spécifique "a" est lié au moment angulaire J et à la masse gravitationnelle du trou noir M par:

(11.1.2)

Rappelons nous aussi (Equation. 10.1.5) :

et nous définissons a par

(11.1.3)

Nous allons utiliser tout ceci dans les coordonnées de Boyer-Lindquist :

(11.1.4)

(11.1.5)

avec les définitions suivantes :

(11.1.6)

(11.1.7)

(11.1.8)

La vitesse angulaire w définit la vitesse angulaire df/dt d’observateurs non localement en rotation qui sont des observateurs avec un paramètre de moment angulaire zéro L_z comme défini dans l’équation (11.1.43).

L’intervalle invariant d’espace temps d’un trou noir chargé en rotation ( Kerr-Newman) est alors:

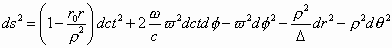
(11.1.9a)

Ce qui peut également s’écrire

(11.1.9b)

où R est le facteur de décalage vers le rouge gravitationnel.

R est donné par :

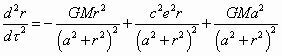
Si on considère la lumière émise par une source localement non en rotation, à une fréquence f0 dans son référentiel propre à r et q constant et observée à distance à la fréquence f’, la lumière va subir un décalage vers le rouge tel que

f ' = Rf₀

Le tenseur métrique covariant pour l’espace temps défini par la solution de Kerr-Newman est donné par:

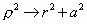
(11.1.10)

Et le tenseur métrique inverse contravariant par :

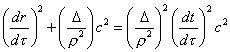
(11.1.11)

L’ordre des index a été choisi comme suit

x⁰ = ct

x¹ = r

x² = q

x³ = f

Dans le cas où :

(11.1.12)

Il va y avoir plus d’un horizon.

L’horizon des évènements extérieur d’un trou noir en rotation chargé, n’est pas défini par le rayon de Schwarzschild r₀ . La distance r₊ associée à l’horizon externe des évènements vaut :

(11.1.13) 

Le second type d’horizon appelé horizon interne des évènements est associé à une distance de :

(11.1.14)

Ce sont simplement les lieux géométriques des points de l’espace temps satisfaisant D= 0.

Une autre surface mathématique remarquable est appelée la limite statique. Cette surface est associée à la distance :

(11.1.15)

Des observateurs distants peuvent observer des objets traverser la limite statique, mais il ne voient jamais un objet traverser l’horizon des évènements à moins que la taille de celui ci ne change. La région entre la limite statique et l’horizon des évènements externes est appelée l’ergosphère. Les objets dans cette région tournent inexorablement dans le sens de rotation du trou noir de Kerr.

La limite statique peut s’obtenir de la façon suivante. Considérons un rayon lumineux se déplaçant dans la direction ± f (autres paramètres spatiaux constants). L’équation 11.1.9b devient :

0 = R²dct² - v ²(df - wdt)²

Ce qui donne :

df/dt = w ± (Rc/v)

(11.1.16)

Toute chose est inéluctablement vouée à se déplacer avec une vitesse angulaire de coordonnée égale à la vitesse de la lumière dans l’ergosphère. La limite statique se produit quand la vitesse de coordonnée de la lumière se déplaçant en contre rotation devient égale à zéro. Ceci implique :

0 = w - (Rc/v)

Résolvons en r,

wv/c = R

w²v²/c² = R²

w²v²/c² = [(D - a²sin²q)/r²] + w²v²/c²

D - a²sin²q = 0

a² + r²a - a²sin²q = 0

r²a + a²(1 - sin²q) = 0

r²a + a²cos²q = 0

r² - r₀r + e² + a²cos²q = 0

(1/2)r² - (GM/c²)r + (1/2)(a²cos²q + e²)

L’équation du second degré en r nous donne bien l’équation 11.1.15.

Cas d’une constante cosmologique non nulle

On peut modifier facilement l’espace temps de Kerr Newman pour modéliser (en première approximation) un trou noir en rotation dans un univers avec une constante cosmologique non nulle en modifiant simplement la définition de a. Posons

a = 1 - r₀/r + e²/r² - (1/3)lr² + r₀/R + (1/3)lR² - e²/R²

(11.1.17)

Si le spin est nul l’espace temps Kerr-Newman-DeSitter correspond à un choix de coordonnées pour un observateur se trouvant à r = R.

Le terme de masse correspond à une attraction en inverse carré de la distance. Le terme de charge correspond à une répulsion en inverse cube de la distance. La constante cosmologique correspond à une force de type « ressort » qui est répulsive si l est positif et donnée par :

mg_cosmological = mc²(1/3)lr.

 (11.1.18)

La solution de Kerr (e = 0) pour un trou noir en rotation mais non chargé peut s ‘exprimer plus simplement par :

 (11.1.19)

Un trou noir de Reissner-Nordstrom est un trou noir chargé mais statique : J = 0.

La solution de Reissner-Nordstrom pour l’intervalle invariant s’exprime plus simplement par :

(11.1.20)

 Il est généralement admis (mais non démontré) que les trous noirs résultant d’un effondrement gravitationnel satisfont l’inégalité :

(11.1.21)

[Bien que les Fermions aient été modélisés par un Vortex, de rayon de Compton voir , http://www.innerx.net/personal/tsmith/Sidharth.html , qui est un espace temps de Kerr-Newman qui résulte de l’union de la relativité et de la mécanique Bohmienne, dans lequel les fermions satisfont à   a² + e² > (GM/c²)²]

Trajectoires d’une particule sur l’axe de symétrie

Dérivons l’équation du mouvement d’une particule neutre en chute libre le long de l’axe de symétrie. Nous allons voir que le spin et la charge vont provoquer une répulsion gravitationnelle à l’approche de la singularité.

Au passage nous verrons aussi qu’on trou noir statique de Reissner Nordström provoque le même effet, la particule en chute libre après avoir franchi les deux horizons va être repoussée et expulsée au-delà de ces deux horizons (dans un autre univers ou une autre région) et cela en un temps propre fini.

(11.1.22)

Et l’équation relative au temps de trajet reliant temps propre et temps de l’observateur distant vaut:

(11.1.23)

Où g est une constante d’intégration appelée habituellement le paramètre d’énergie

Pour un trou noir de Kerr Newman nous avons,

Eq. (11.1.22) devient :

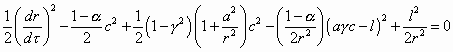(11.1.24)

Regardons au passage, pour un trou noir de Reissner-Nordstrom, (J = 0), ce que cela donne :

(11.1 .25)

Nous y reviendrons plus loin

Comme il est généralement admis que la charge, la masse et le moment angulaire propre sont les seuls paramètres caractéristiques d’un trou noir l’équation 11.1.3 peut servie à définir a . Cependant, on peut aussi considérer l’introduction de champs massifs (massifs dans lesquels r_Totc² = g_mnT^mn ¹ 0) qui pourraient aussi entrer dans la définition de a. Le tenseur énergie impulsion de tels espaces posent des problèmes dans le cas d’un univers avec un seul trou noir, mais si on considère un trou noir avec ces autres champs, on obtiendrait toujours les équations 1a et1b. Cependant si on exprime a en série de Laurent tronquée pour b_m de telle sorte que m > 2 , on obtient une singularité ponctuelle dans l’équation 1a, à l’origine à la place de la singularité en anneau. De même pour m > 2, le signe du dernier terme de la série va déterminer si une particule neutre en chute libre va être soumise à une attraction ou à une répulsion gravitationnelle, lorsqu’elle s’approche de r = 0. Si on ajoute une série de Taylor à a et que la série est tronquée à n’importe quel a_n n > 0, l’équation 1b s’annule à l’infini. Comme, nous définissons typiquement notre observateur distant à l’infini, une telle généralisation exigerait que a soit normalisé à 1 à l’infini. Donc, si on ajoute une série de Taylor à la définition de a , elle ne doit pas être tronquée pour que nous puissions physiquement définir des observateurs à l’infini.

L’intervalle invariant dans cette métrique est défini par 11.1.9

Calcul pour une géodésique polaire

Comme nous ne considérons que le mouvement polaire dq = 0, q = 0 ou p et v(r)= 0, .

L’équation (11.1.9) se simplifie et devient :

(11.1.26)

ds = dct , nous pouvons le réécrire :

(11.1.27)

Nous avons maintenant tout ce qu’il nous faut pour établir l’équation du mouvement dt/dt . Utilisons l’équation géodésique.

L’équation pour x⁰ = ct, est :

(11.1.28)

En développant avec dq = 0 pour le mouvement polaire on obtient :

(11.1.29)

Le seul G ^l_mn non nul pour le cas q = 0 ou p est G ⁰₀₁.

On obtient donc :

(11.1.30)

Développons la connexion :

(11.1.31)

Les coefficients de la métrique sont

g₀₁ = g₃₁ = g₁₀ = 0. Pour q = 0 ou p, on a aussi g₃₀ = 0, quel que soit r alors g₃₀,₁ = 0 , cela donne :

(11.1.32)

On substitue dans (11.1.30) :

(11.1.33)

On simplifie:

(11.1.34)

Remarquons que pour q = 0, p , g⁰⁰ = r²/D = 1/g₀₀ , alors l’équation devient :

(11.1.35)

On sépare les variables, on intègre en remplaçant g⁰⁰ par r²/D et on simplifie:

(11.1.36)

Rappelons que g est une constante appelée paramètre d’énergie.

Pour q = 0 ou p ceci peut aussi être écrit comme :

En insérant (1.11.23) dans (11.1.27), on obtient:

(11.1.37)

Pour q = 0 ou p , cela devient:

Equation du mouvement polaire [ r(τ )] :

(11.1.38)

Ces équations sont pour le mouvement polaire,

Equation du mouvement équatorial [ r(τ) ]

on peut les comparer à celles du mouvement équatorial qui est donné par l’expression:

(11.1.39)

En différentiant (1.1.38) par rapport à t, en utilisant la règle de Leibnitz, et en simplifiant on obtient:

(11.1.22)

Avec et r₀ = 2GM/c² pour le trou noir de Kerr-Newman et en différentiant par rapport à r, on obtient:

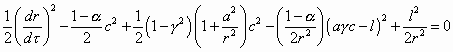(11.1.24)

Cette équation n’est pas évidente à résoudre, étudions un cas particulier.

Cas Reissner Nordström : mise en évidence de la répulsion centrale

Pour un trou noir de Reissner-Nordstrom, J = 0 donc a = 0, cela donne :

(11.1.25)

Considérons le cas extrémal où et e » GM/c². Les deux horizons coïncident alors à r_± = GM/c² et l’équation devient:

(11.1.40)

La répulsion en r ^-3 domine à courte distance sur l’attraction en r ^-2 pour r petit.

La répulsion commence par dominer quand d²r/dt² = 0. Ceci se produit pour:

r = GM/c².

C’est la distance à l’horizon (double). Comme la répulsion n’est pas prépondérante avant que la particule atteigne l’horizon, celle ci peut franchir l’horizon externe et interne puis, compte tenu de la répulsion conformément à (11.1.25) qui augmente la particule est expulsée du trou noir (ailleurs).

Pour résumer, nous avons vu que la présence d’une charge dans un trou noir a pour conséquence de générer un champ gravitationnel répulsif, qui domine le champ classique attractif à courte distance de la singularité.

Nous avons établi le mouvement géodésique polaire pour une particule neutre en chute libre vers le trou noir. A une distance suffisamment courte les effets de rotation dominent sur l’attraction due à la masse et le répulsion due à la charge électrique. Nous avons vu qu’en l’absence de rotation le mouvement géodésique a un point de rebroussement à l’intérieur du trou noir qui conduit à expulser celle ci du trou noir, en un temps fini.

Période des orbites

Maintenant considérons le mouvement circulaire autour d’un trou noir de Schwarzschild

En mécanique Newtonienne la troisième loi de Kepler’s définit la relation entre le période de l’orbite et le demi grand axe.

T ² = (4p²/GM)a³

(11.1.41a)

On considère une particule de test dans un espace temps de Schwarzschild. Si r est la coordonnée radiale et T la coordonnée temporelle pour un observateur distant, on remarque que l’équation de Kepler est toujours valide à toutes les distances du trou noir.

T ² = (4p²/GM)r³

(11.1.41b)

Cependant les orbites sous la sphère des photons, exigeraient une vitesse orbitale que la vitesse de la lumière (en coordonnées à distance), donc, pas d’orbites circulaires sous la sphère des photons (r = 3GM/c²). Il y a différentes façons d’obtenir les lois de Képler des équations de la RG.

Ici nous utilisons le principe extrémal (du temps propre). Pour le mouvement équatorial

ds² = (1 - r₀/r)dct² - r²df ²

en utilisant 2p/T = df/dt, et ds = dt , ceci devient

dt = [1 - r₀/r - r²(2p/T)²/c²]^1/2dt

L’intégration sur une orbite entière donne :

t_1orbite = [1 - r₀/r - r²(2p/T)²/c²]^1/2T

Pour maximiser le temps propre pour un temps orbital fixe, on doit simplement dériver [1 - r₀/r - r²(2p/T)²/c²]^1/2 par rapport à r et le poser égal à zéro.

En utilisant r₀ = 2GM/c² cela donne :

(2GM/r²c² - 2r(2p/T)²/c²)(1/2) / [1 - r₀/r - r²(2p/T)²/c²]^1/2 = 0

Simplifions, on voit que cela donne la troisième loi de Képler.

T ² = (4p²/GM)r³

En général, on peut décrire un mouvement arbitraire autour des types de trous noirs cités ci dessus en utilisant les définitions générales (11.1.4 à 11.1.8 ) pour définir les constantes du mouvement.

(11.1.42)

(11.1.43)

Les équations ci dessus sont dérivées à la fin du paragraphe. En utilisant ces équations avec (11.1.9) et pour un mouvement équatorial q = p/2, et L_z = L, ce qui après un peu de calcul se simplifie en

Si la charge est nulle, l’équation du mouvement géodésique associée à un trou noir de Kerr peut s’écrire :

(11.1.44)

A l’intérieur de la limite statique, on tourne forcément avec le trou noir, il n’y a pas d’observateurs statiques en deçà de cette limite.

Robert M. Wald dans « General Relativity » définit l’état le plus proche d’un observateur qui n’est pas entraîné par la rotation qu’il appelle «  observateur localement non en rotation »comme étant ceux de vitesse angulaire de coordonnée W. Dans son texte c’est donné par

W = w

Où w est donné par ( 11.1.8 )

Ces observateurs sont simplement ceux pour qui L_z = 0 comme défini ci dessus.

La vitesse angulaire du trou noir est définie par :

W_H = ac/(r₊² + a²) (11.1.45)

Précession des orbites 

Quand on dispose d’une équation du mouvement sous la forme (11.1.46) et la loi de force centrale, ce qui est décrit n’est pas exactement soit k/r² soit kr, alors le orbites décrites sont des ellipses qui elles mêmes tournent. L’aphélie et le périhélie sont les endroits où les planètes en orbite sont au plus loin ou au plus près du Soleil. Dans le cas où la loi de la force prend la forme :

(11.1.46)

Ce qui est le cas, dans le mouvement équatorial d’un espace temps de Kerr Newman (on peut vérifier en différentiant simplement (11.1.39) par rapport au temps propre. L’équation de précession angulaire du périhélie ou de l’aphélie par orbite est donnée approximativement par :

(11.1.47)

Où R est le rayon moyen orbital pour des orbites quasi circulaires.

Cette équation donne l’équation de l’avance du périhélie en radians pour tout mouvement qui respecte une équation de la forme (11.1.46) quel que soit g( r ), fonction de r.

d²r/dt² + GM/r² - l²/r³ = 0 (11.1.48a)

où l peut être :

l ² = GMR(1 - e²) où R est le demi grand axe et e est l’excentricité de l’orbite.

Pour g( r ) nous utiliserons

G( r ) = - GM/r²

g’( r ) = 2GM/r³

Rg’( r )/g( r ) = R(2GM/R³)/(-GM/R²) = -2

Si on insère cela dans (11.1.47) on obtient

Dq_p = 0

Pas d’avance de périhélie pour le Soleil seul. Si a = 0 (Schwarzschild) et si on différentie (11.1.44) on arrive à :

d²r/dt² + GM/r² + 3(GM/r⁴)(l/c)² - l²/r³ = 0 (11.1.48b)

Pour g( r ) on utilisera

G( r) = - GM/r² - 3(GM/r⁴)(l/c)²

g’( r ) = 2GM/r³ + 12(GM/r⁵)(l/c)²

Rg’( r )/g( r ) = R(2GM/R³ + 12(GM/R⁵)(l/c)²)/( - GM/R² - 3(GM/R⁴)(l/c)²) = - 2 - [6R(GM/R⁵)(l/c)²/(GM/R² + 3(GM/R⁴)(l/c)²)]

Approximé à:

Rg’( r )/g( r ) » - 2 - 6(l/c)²/R² » - 2 - 6(RGM(1 - e²))/R²c² = - 2 - 6GM(1 - e²)/Rc²

Insérons dans équation (11.1.47), on obtient :

Dq_p = 2p[(3 - 2 - 6GM(1 - e²)/Rc²)^-1/2 - 1]/(1 - e²)²

Dq_p = 2p[(1 - 6GM(1 - e²)/Rc²)^-1/2 - 1]/(1 - e²)²

Approximé à :

Dq_p » 2p[1 + 3(1 - e²)GM/Rc² - 1]/(1 - e²)²

Dq_p = 6pGM/Rc²(1 - e²) (11.1.49)

Dq_p = 6p(6.7x10^-11)(2.0x10³⁰)/(5.8x10¹⁰)(3.0x10⁸)²(1 - 0.206²)

Dq_p = 5.0x10^-7

Ceci en radian par révolution. La période de Mercure est de 0,16 An, donc par siècle l’avance en Radian est :

Dq_p100 = 5.0x10^-7(100/0.16) = 3.1x10^-4

Avec 2.06 x10⁵ secondes d’arc par radian, exprimé en secondes d’arc, cela fait :

Dq_p100 = 3.1x10^-4(2.06 x10⁵) »

Dq_p100 = 64 »

Nous avons négligé, l’aplatissement du Soleil etc.. Donc la réponse est plus élevée que ce qu’on aurait obtenu par une méthode moins approximative. En incluant les effets relativistes significatifs on réduirait la marge d’erreur, mais déjà la réponse est plus satisfaisante que celle donnée par la loi de Newton, vis à vis des (41 +/- 2) » observés.

Méthode en utilisant les vecteurs de Killing 

Pour finir établissons les constantes du mouvement géodésique pour une métrique de Kerr-Newman à partir des vecteurs de Killing..

La métrique est indépendante de t et de f , ceci nous définit deux vecteurs T = e_ct, et F = e_f.

Le premier nous donne une quantité conservée dans le mouvement géodésique que nous appellerons le paramètre d’énergie E_cons pour lequel nous définissons g par, g = E_cons/mc².

gc = g_mnT^mUⁿ

gc = g₀₀T⁰U⁰ + g_0fT⁰U^f

gc = g₀₀(dct/dt) + g_0f(df/dt)

Ceci nous donne l’équation (11.1.42)

Nous avons ajouté à E un indice « cons » ici pour bien distinguer ce paramètre d’énergie conservé de l’énergie E que nous réservons pour la composante temporelle du quadrivecteur impulsion contravariante qui n’est pas conservée dans des espaces temps arbitraires.

Le deuxième vecteur de Killing est associé à une autre quantité conservée du mouvement géodésique le paramètre de moment angulaire, l_z = L_z/m

- l_z = g_mnF^mUⁿ

- l_z = g_ffF^fU^f + g_f0F^fU⁰

l_z = - g_f0(dct/dt) - g_ff(df/dt)

Ceci nous donne l’équation.(11.1.43)